Связанные коэффициенты

В дифференциальном исчислении, связанные коэффициенты связаны с поиском скорости, при которой величина изменения на , связывающие это количество с другими величинами, скорость изменения которых известна. Скорость изменения обычно относится к времени. Поскольку наука и инженерия часто связывают количества друг с другом, методы связанных скоростей имеют широкое применение в этих областях. Дифференциация по времени или по одной из других переменных требует применения правила цепочки , так как большинство проблем связано с несколькими переменными.

По сути, если функция $F\; \{\backslash \; displaystyle\; F\}$определена так, что $F\; =\; f\; (x)\; \{\backslash \; displaystyle\; F\; =\; f\; (x)\}$, тогда производная функции $F\; \{\backslash \; displaystyle\; F\}$может быть взята по другой переменной. Мы предполагаем, что $x\; \{\backslash \; displaystyle\; x\}$является функцией от $t\; \{\backslash \; displaystyle\; t\}$, т.е. $x\; =\; g\; (t)\; \{\backslash \; displaystyle\; х\; =\; g\; (t)\}$. Тогда $F\; =\; f\; (g\; (t))\; \{\backslash \; displaystyle\; F\; =\; f\; (g\; (t))\}$, поэтому

$F\; \prime \; =\; f\; \prime \; (g\; (t))\; \cdot \; g\; \prime \; (T)\; \{\backslash \; displaystyle\; F\; \text{'}=\; f\text{'}\; (g\; (t))\; \backslash \; cdot\; g\; \text{'}(t)\}$

Записано в нотации Лейбница, это:

$d\; F\; dt\; =\; dfdx\; \cdot \; dxdt.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dF\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{df\}\; \{dx\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}.\}$

Таким образом, если известно, как $x\; \{\backslash \; displaystyle\; x\}$изменяется относительно $t\; \{\backslash \; displaystyle\; t\}$, тогда мы можем определить, как $F\; \{\backslash \; displaystyle\; F\}$изменяется по отношению к $t\; \{\backslash \; displaystyle\; t\}$и наоборот. Мы можем расширить это применение цепного правила с помощью правил исчисления суммы, разности, произведения и частного и т. Д.

Например, если $F\; (x)\; =\; G\; (y)\; +\; H\; (z)\; \{\backslash \; Displaystyle\; F\; (x)\; =\; G\; (y)\; +\; H\; (z)\}$, тогда

$d\; F\; dx\; \cdot \; dxdt\; =\; d\; G\; dy\; \cdot \; dydt\; +\; d\; H\; dz\; \cdot \; dzdt.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dF\}\; \{dx\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{dG\}\; \{dy\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; +\; \{\; \backslash \; frac\; \{dH\}\; \{dz\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{dz\}\; \{dt\}\}.\}$

• 1 Процедура
• 2 Примеры
  • 2.1 Пример наклонной лестницы
• 3 Физические примеры
  • 3.1 Физический пример I: относительная кинематика двух транспортных средств
  • 3.2 Физический пример II: Электромагнитная индукция проводящей петли, вращающейся в магнитном поле
• 4 Ссылки

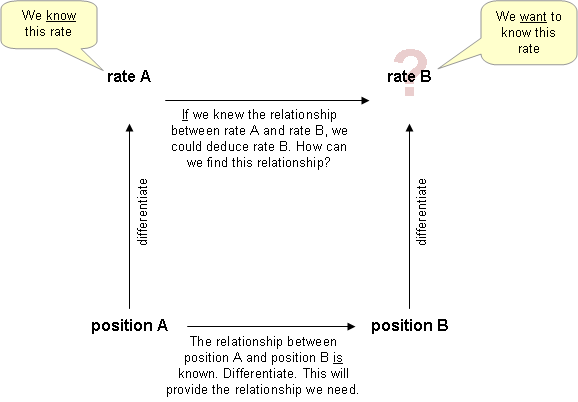
Самый распространенный способ Проблемы, связанные со скоростью, заключаются в следующем:

1. Определите известные переменные, включая скорости изменения и скорость изменения, которую необходимо найти. (Изображение или представление проблемы может помочь сохранить все в порядке)
2. Постройте уравнение, связывающее величины, скорость изменения которых известна, с величиной, скорость изменения которой равна
3. Продифференцируйте обе части уравнения относительно времени (или другой скорости изменения). Часто на этом этапе используется правило цепочки .
4. Подставьте известные скорости изменения и известные величины в уравнение.
5. Найдите желаемую скорость изменения.

Ошибки в этой процедуре часто вызваны подстановкой известных значений переменных до (а не после) нахождения производной по времени. Это приведет к неверному результату, поскольку, если эти значения подставить вместо переменных перед дифференцированием, эти переменные станут константами; и когда уравнение дифференцируется, нули появляются в местах всех переменных, для которых были вставлены значения.

Пример наклонной лестницы

10-метровая лестница прислонена к стена здания, а основание лестницы отодвигается от здания со скоростью 3 метра в секунду. Как быстро верхняя часть лестницы скользит по стене, если ее основание находится на расстоянии 6 метров от стены?

Расстояние между основанием лестницы и стеной, x, и высота лестницы на стене, y, представляют стороны прямоугольного треугольника с лестницей в качестве гипотенуза, h. Цель состоит в том, чтобы найти dy / dt, скорость изменения y по времени, t, когда известны h, x и dx / dt, скорость изменения x.

Шаг 1:

$x\; =\; 6\; \{\backslash \; displaystyle\; x\; =\; 6\}$

$h\; =\; 10\; \{\backslash \; displaystyle\; h\; =\; 10\}$

$dxdt\; =\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; =\; 3\}$

$dhdt\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dh\}\; \{dt\}\}\; =\; 0\}$

$dydt\; =?\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; =\; \{\backslash \; text\; \{?\}\}\}$

Шаг 2: из теоремы Пифагора уравнение

$x\; 2\; +\; y\; 2\; =\; h\; 2,\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; =\; h\; ^\; \{2\},\; \backslash ,\}$

описывает взаимосвязь между x, y и h для прямоугольного треугольника. Дифференцируя обе части этого уравнения по времени, t, получаем

$ddt\; (x\; 2\; +\; y\; 2)\; =\; ddt\; (h\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (h\; ^\; \{2\})\}$

Шаг 3: После определения желаемой скорости изменения dy / dt дает нам

$ddt\; (x\; 2)\; +\; ddt\; (y\; 2)\; =\; ddt\; (h\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (x\; ^\; \{2\})\; +\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (y\; ^\; \{2\})\; =\; \{\backslash \; гидроразрыва\; \{d\}\; \{dt\}\}\; (h\; ^\; \{2\})\}$

$(2\; x)\; dxdt\; +\; (2\; y)\; dydt\; =\; (2\; h)\; dhdt\; \{\backslash \; displaystyle\; (2x)\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; +\; (2y)\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; =\; (2h)\; \{\backslash \; frac\; \{dh\}\; \{dt\}\}\}$

$xdxdt\; +\; ydydt\; =\; hdhdt\; \{\backslash \; displaystyle\; x\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; +\; y\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; =\; h\; \{\backslash \; frac\; \{dh\}\; \{dt\}\}\}$

$dydt\; =\; hdhdt\; -\; xdxdty.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{h\; \{\backslash \; frac\; \{dh\}\; \{dt\}\}\; -\; x\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\}\; \{y\}\}.\}$

Шаг 4 и 5: Использование переменных из шага 1 дает нам:

$dydt\; =\; hdhdt\; -\; xdxdty.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{h\; \{\backslash \; frac\; \{dh\}\; \{dt\}\}\; -\; x\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\}\; \{y\}\}.\}$

$dydt\; =\; 10\; \times \; 0\; -\; 6\; \times \; 3\; y\; =\; -\; 18\; лет.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{10\; \backslash \; times\; 0-6\; \backslash \; times\; 3\}\; \{y\}\}\; =\; -\; \{\backslash \; frac\; \{18\}\; \{y\}\}.\}$

Решение для y с использованием теоремы Пифагора дает:

$x\; 2\; +\; y\; 2\; =\; h\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; =\; h\; ^\; \{2\}\}$

$6\; 2\; +\; y\; 2\; =\; 10\; 2\; \{\backslash \; displaystyle\; 6\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; =\; 10\; ^\; \{2\}\}$

$y\; =\; 8\; \{\backslash \; displaystyle\; y\; =\; 8\}$

Подставляем 8 для уравнения:

$-\; 18\; y\; =\; -\; 18\; 8\; =\; -\; 9\; 4\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{18\}\; \{y\}\}\; =\; -\; \{\backslash \; frac\; \{18\}\; \{8\}\}\; =\; -\; \{\backslash \; frac\; \{9\}\; \{4\}\}\}$

Обычно предполагается, что отрицательные значения представляют направление вниз. При этом верх лестницы скользит по стене со скоростью ⁄ 4 метра в секунду.

Поскольку одна физическая величина часто зависит от другой, которая, в свою очередь, зависит от других, таких как время, методы связанных скоростей имеют широкое применение в физике. В этом разделе представлен пример взаимосвязанных скоростей кинематики и электромагнитной индукции.

Физический пример I: относительная кинематика двух транспортных средств

Одно транспортное средство движется на север и в настоящее время находится в точке (0,3) ; другая машина направляется на запад и в настоящее время находится в (4,0). Цепное правило можно использовать, чтобы определить, приближаются ли они друг к другу или отдаляются друг от друга.

Например, можно рассмотреть проблему кинематики, когда одно транспортное средство движется на запад к перекрестку со скоростью 80 миль в час, а другое - на север от перекресток со скоростью 60 миль в час. Можно спросить, сближаются ли транспортные средства или дальше друг от друга и с какой скоростью в тот момент, когда транспортное средство, направляющееся на север, находится в 3 милях к северу от перекрестка, а транспортное средство, направляющееся на запад, находится в 4 милях к востоку от перекрестка.

Большая идея: использовать цепное правило для вычисления скорости изменения расстояния между двумя транспортными средствами.

План:

1. Выбрать систему координат
2. Определить переменные
3. Нарисуйте картинку
4. Большая идея: использовать правило цепочки для вычисления скорости изменения расстояния между двумя транспортными средствами
5. Выразите c через x и y по теореме Пифагора
6. Выразите dc / dt, используя цепное правило, через dx / dt и dy / dt
7. Замените на x, y, dx / dt, dy / dt
8. Упростить.

Выбрать систему координат: Пусть ось y указывает на север, а ось x - на восток.

Идентификация переменных: Определите y (t) как расстояние транспортного средства, движущегося на север от исходной точки, и x (t) как расстояние от транспортного средства, направляющегося на запад от исходной точки.

Выразите c через x и y с помощью теоремы Пифагора:

$c\; =\; (x\; 2\; +\; y\; 2)\; 1/2\; \{\backslash \; displaystyle\; c\; =\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{1/2\}\}$

Выразите dc / dt, используя правило цепочки в терминах dx / dt и dy / dt:

$dcdt\; =\; ddt\; (x\; 2\; +\; y\; 2)\; 1/2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dc\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{1/2\}\}$	Применить оператор производной ко всей функции
$=\; 1\; 2\; (x\; 2\; +\; y\; 2)\; -\; 1/2\; ddt\; (x\; 2\; +\; y\; 2)\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{-\; 1/2\}\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\}$	Квадратный корень вне функции; Сумма квадратов находится внутри функции
$=\; 1\; 2\; (x\; 2\; +\; y\; 2)\; -\; 1/2\; [ddt\; (x\; 2)\; +\; ddt\; (y\; 2)]\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{-\; 1/2\}\; \backslash \; left\; [\{\backslash \; frac\; \{d\}\; \{dt\}\}\; (x\; ^\; \{2\})\; +\; \{\backslash \; frac\; \{d\}\; \{dt\}\; \}\; (y\; ^\; \{2\})\; \backslash \; right]\}$	Оператор дифференцирования распределения
$=\; 1\; 2\; (x\; 2\; +\; y\; 2)\; -\; 1/2\; [2\; xdxdt\; +\; 2\; ydydt]\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{\; 1\}\; \{2\}\}\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{-\; 1/2\}\; \backslash \; left\; [2x\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; +\; 2y\; \{\backslash \; frac\; \{dy\}\; \{dt\; \}\}\; \backslash \; right]\}$	Применить правило цепочки к x (t) и y (t)}
$=\; xdxdt\; +\; ydydtx\; 2\; +\; y\; 2\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{x\; \{\backslash \; frac\; \{dx\}\; \{\; dt\}\}\; +\; y\; \{\backslash \; frac\; \{dy\}\; \{dt\}\}\}\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\}\}\}$	Упростить.

Подставляем в x = 4 мили, y = 3 мили, dx / dt = −80 миль / час, dy / dt = 60 миль / час и упрощаем

$dcdt\; =\; 4\; mi\; \cdot \; (\; -\; 80\; миль\; /\; час)\; +\; 3\; мили\; \cdot \; (60)\; миль\; /\; час\; (4\; мили)\; 2\; +\; (3\; мили)\; 2\; =\; -\; 320\; миль\; 2\; /\; час\; +\; 180\; миль\; 2\; /\; час\; 5\; миль\; =\; -\; 140\; миль\; 2\; /\; час\; 5\; mi\; =\; -\; 28\; миль\; /\; час\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{dc\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{4\; \{\backslash \; text\; \{mi\}\}\; \backslash \; cdot\; (-80\; \{\backslash \; text\; \{mi\; \}\}\; /\; \{\backslash \; text\; \{hr\}\})\; +\; 3\; \{\backslash \; text\; \{mi\}\}\; \backslash \; cdot\; (60)\; \{\backslash \; text\; \{mi\}\}\; /\; \{\backslash \; text\; \{hr\}\}\}\; \{\backslash \; sqrt\; \{(4\; \{\backslash \; text\; \{mi\}\})\; ^\; \{2\}\; +\; (3\; \{\backslash \; text\; \{mi\}\})\; ^\; \{2\}\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{-320\; \{\backslash \; text\; \{mi\}\}\; ^\; \{2\}\; /\; \{\; \backslash \; text\; \{hr\}\}\; +\; 180\; \{\backslash \; text\; \{mi\}\}\; ^\; \{2\}\; /\; \{\backslash \; text\; \{hr\}\}\}\; \{5\; \{\backslash \; text\; \{mi\}\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{-140\; \{\; \backslash \; text\; \{mi\}\}\; ^\; \{2\}\; /\; \{\backslash \; text\; \{hr\}\}\}\; \{5\; \{\backslash \; text\; \{mi\}\}\}\}\; \backslash \backslash \; =\; -\; 28\; \{\backslash \; text\; \{mi\}\}\; /\; \{\backslash \; text\; \{hr\}\; \}\; \backslash \; end\; \{align\}\}\}$

Следовательно, две машины сближаются со скоростью 28 миль в час.

Физический пример II: Электромагнитная индукция проводящей петли, вращающейся в магнитном поле

магнитный поток через петлю области A, нормаль которой находится под углом θ к магнитному полю. поле напряженности B равно

$\Phi \; B\; =\; BA\; cos\; \; (\theta ),\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{B\}\; =\; BA\; \backslash \; cos\; (\backslash \; theta),\}$

закон Фарадея электромагнитной индукции гласит, что индуцированная электродвижущая сила $E\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\}$- отрицательная скорость изменения магнитного потока $\Phi \; B\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{B\}\}$через токопроводящую петлю.

$E\; =\; -\; d\; \Phi \; B\; dt,\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\; =\; -\; \{\{d\; \backslash \; Phi\; \_\; \{B\}\}\; \backslash \; over\; dt\},\}$

Если площадь контура A и магнитное поле B остаются постоянными, но петля поворачивается так, чтобы угол θ был известной функцией времени, скорость изменения θ может быть связана со скоростью изменения $\Phi \; B\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{B\; \}\}$(и, следовательно, электродвижущая сила), взяв производную по времени отношения магнитного потока

$E\; =\; -\; d\; \Phi \; B\; dt\; =\; BA\; sin\; \; \theta \; d\; \theta \; dt\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\; \}\}\; =\; -\; \{\backslash \; frac\; \{d\; \backslash \; Phi\; \_\; \{B\}\}\; \{dt\}\}\; =\; BA\; \backslash \; sin\; \backslash \; theta\; \{\backslash \; frac\; \{d\; \backslash \; theta\}\; \{dt\}\}\}$

Если, например, цикл вращается при постоянной угловой скорости ω, так что θ = ωt, тогда

$E\; =\; \omega \; BA\; sin\; \; \omega \; t\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\; =\; \backslash \; omega\; BA\; \backslash \; sin\; \backslash \; omega\; t\}$