Лемма Линдстрема – Гесселя – Виенно

редактировать

Подсчитывает количество наборов непересекающихся путей решетки

В математике Лемма Линдстрема – Гесселя – Венно предоставляет способ подсчета количества кортежей непересекающихся решеточных путей. Это было доказано Гесселем-Венно в 1985 году на основе предыдущей работы Линдстрёма, опубликованной в 1973 году.

Содержание

1 Утверждение
2 Доказательство
3 Приложения
- 3.1 Полиномы Шура
- 3.2. Формула Коши – Бине
4 Обобщения
- 4.1 Формула Таласки
5 См. Также
6 Ссылки

Утверждение

Пусть G - локально конечный ориентированный ациклический граф. Это означает, что каждая вершина имеет конечную степень и что G не содержит направленных циклов. Рассмотрим базовые вершины $A = {a 1,…, an} {\ displaystyle A = \ {a_ {1}, \ ldots, a_ {n} \}}$ $A = \ {a_ {1}, \ ldots, a_ {n} \}$ и конечные вершины $B = {b 1,…, bn} {\ displaystyle B = \ {b_ {1}, \ ldots, b_ {n} \}}$ $B = \ { b_ {1}, \ ldots, b_ {n} \}$ , а также присвоить вес $ω e { \ displaystyle \ omega _ {e}}$ $\ omega _ {{e}}$ до каждого направленного ребра e. Предполагается, что эти веса ребер принадлежат некоторому коммутативному кольцу. Для каждого направленного пути P между двумя вершинами пусть $ω (P) {\ displaystyle \ omega (P)}$ $\ omega (P)$ будет произведением весов ребер пути. Для любых двух вершин a и b напишите сумму e (a, b) $e (a, b) = ∑ P: a → b ω (P) {\ displaystyle e (a, b) = \ sum _ {P: a \ to b} \ omega (P)}$ $e (a, b) = \ sum _ {{P: a \ к b}} \ omega (P)$ по всем путям от a до b. Это хорошо определено, если между любыми двумя точками есть только конечное число путей; но даже в общем случае это может быть хорошо определено при некоторых обстоятельствах (например, все веса ребер являются попарно различными формальными неопределенными, и $e (a, b) {\ displaystyle e (a, b)}$ $e(a,b)$ рассматривается как формальный степенной ряд). Если присвоить каждому ребру вес 1, то e (a, b) подсчитывает количество путей от a до b.

При такой настройке напишите

M = (e (a 1, b 1) e (a 1, b 2) ⋯ e (a 1, bn) e (a 2, b 1) e (a 2, b 2) ⋯ e (a 2, bn) ⋮ ⋮ ⋱ ⋮ e (an, b 1) e (an, b 2) ⋯ e (an, bn)) {\ displaystyle M = {\ begin { pmatrix} e (a_ {1}, b_ {1}) e (a_ {1}, b_ {2}) \ cdots e (a_ {1}, b_ {n}) \\ e (a_ {2}, b_ {1}) e (a_ {2}, b_ {2}) \ cdots e (a_ {2}, b_ {n}) \\\ vdots \ vdots \ ddots \ vdots \\ e (a_ {n}, b_ {1}) e (a_ {n}, b_ {2}) \ cdots e (a_ {n}, b_ {n}) \ end {pmatrix}}}

M = {\ begin {pmatrix} e (a_ {1}, b_ {1}) e (a_ {1}, b_ {2}) \ cdots e (a_ {1}, b_ {n}) \\ e (a_ {2}, b_ {1}) e (a_ {2}, b_ {2}) \ cdots e (a_ {2}, b_ {n }) \\\ vdots \ vdots \ ddots \ vdots \\ e (a_ {n}, b_ {1}) e (a_ {n}, b_ {2}) \ cdots e (a_ {n}, b_ {n}) \ end {pmatrix}}

Кортеж из n непересекающихся путей от A до B означает набор из n (P 1,..., P n) путей в G со следующими свойствами:

Там существует перестановка $σ {\ displaystyle \ sigma}$ $\ sigma$ из ${1, 2,..., n} {\ displaystyle \ left \ {1,2,..., n \ right \}}$ $\ left \ {1,2,..., n \ right \}$ такой, что для каждого i путь P i является путем от $ai {\ displaystyle a_ {i}}$ $a_ {i}$ до $b σ (i) {\ displaystyle b _ {\ sigma (i)}}$ $b _ {{\ sigma (i)} }$ .
всякий раз, когда $i ≠ j {\ displaystyle i \ neq j}$ $i \ neq j$ , пути P i и P j не имеют двух общих вершин (даже конечных точек).

Учитывая такой кортеж n (P 1,..., P n), мы обозначаем $σ (P) {\ displaystyle \ sigma (P)}$ $\ sigma (P)$ перестановка $σ {\ displaystyle \ sigma}$ $\ sigma$ из первого условия.

Лемма Линдстрема – Гесселя – Венно затем утверждает, что определитель M является суммой со знаком по всем n-кортежам P = (P 1,..., P n) непересекающихся путей из A в B:

det (M) = ∑ (P 1,…, P n): A → B sign (σ (P)) ∏ i = 1 n ω (P i). {\ Displaystyle \ Det (M) = \ сумма _ {(P_ {1}, \ ldots, P_ {n}) \ двоеточие от A \ до B} \ mathrm {знак} (\ sigma (P)) \ prod _ { i = 1} ^ {n} \ omega (P_ {i}).}

\ det (M) = \ sum _ {{(P_ {1 }, \ ldots, P_ {n}) \ двоеточие A \ to B}} {\ mathrm {sign}} (\ sigma (P)) \ prod _ {{i = 1}} ^ {n} \ omega (P_ {i}).

То есть определитель M считает веса всех наборов из n непересекающихся путей, начинающихся в A и заканчивающихся в B, каждый со знаком соответствующей перестановки $(1, 2,…, n) {\ displaystyle (1,2, \ ldots, n)}$ $(1,2, \ ldots, n)$ , заданной как $P i { \ displaystyle P_ {i}}$ $P_ {i}$ принимает $ai {\ displaystyle a_ {i}}$ $a_i$ на $b σ (i) {\ displaystyle b _ {\ sigma (i)}}$ $b _ {{\ sigma (i)} }$ .

В частности, если единственная возможная перестановка - это тождество (т. Е. Каждый набор из n непересекающихся путей от A до B принимает a i на b i для каждого i), и мы берем веса равными 1, тогда det (M) - это в точности количество непересекающихся наборов путей, начинающихся в A и заканчивающихся в B.

Доказательство

Для доказательства леммы Линдстрема – Гесселя – Виенно сначала введем некоторые обозначения.

n -путь от кортежа из n $(a 1, a 2,…, an) {\ displaystyle (a_ {1}, a_ {2}, \ ldots, a_ {n})}$ $(a_1, a_2, \ ldots, a_n)$ вершин G в кортеж из n $(b 1, b 2,…, bn) {\ displaystyle (b_ {1}, b_ {2}, \ ldots, b_ {n})}$ ${\ displaystyle (b_ {1}, b_ {2}, \ ldots, b_ {n}) }$ вершин G будет означать кортеж из n $(P 1, P 2,…, P n) {\ displaystyle (P_ {1}, P_ {2}, \ ldots, P_ {n})}$ $(P_ {1}, P_ {2}, \ ldots, P_ {n})$ путей в G, каждый $P i {\ displaystyle P_ {i}}$ $P_ {i}$ , ведущий от $от ai {\ displaystyle a_ {i}}$ $a_ {i}$ до $bi {\ displaystyle b_ {i}}$ $b_{i}$ . Этот n-путь будет называться непересекающимся на случай, если пути P i и P j не имеют двух общих вершин (включая конечные точки) всякий раз, когда $я ≠ J {\ Displaystyle I \ NEQ J}$ $i \ neq j$ . В противном случае он будет называться запутанным .

Учитывая n-путь $P = (P 1, P 2,…, P n) {\ displaystyle P = (P_ {1}, P_ {2}, \ ldots, P_ {n})}$ ${\ displaystyle P = (P_ {1}, P_ {2}, \ ldots, P_ {n})}$ , вес $ω (P) {\ displaystyle \ omega (P)}$ $\ omega (P)$ этого n -путь определяется как произведение $ω (P 1) ω (P 2) ⋯ ω (P n) {\ displaystyle \ omega (P_ {1}) \ omega (P_ {2}) \ cdots \ omega ( P_ {n})}$ $\ omega (P_ {1}) \ omega (P_ {2}) \ cdots \ omega (P_ {n})$ .

A скрученный n -путь из n-кортежа $(a 1, a 2,…, an) {\ displaystyle (a_ {1}, a_ {2}, \ ldots, a_ {n})}$ $(a_1, a_2, \ ldots, a_n)$ вершин G в кортеж из n $(b 1, b 2,…, bn) {\ displaystyle (b_ {1 }, b_ {2}, \ ldots, b_ {n})}$ ${\ displaystyle (b_ {1}, b_ {2}, \ ldots, b_ {n}) }$ вершин G будет означать n-путь из $(a 1, a 2,…, an) {\ displaystyle (a_ {1}, a_ {2}, \ ldots, a_ {n})}$ $(a_1, a_2, \ ldots, a_n)$ до $(b σ (1), b σ (2),…, b σ (n)) {\ displaystyle \ left (b _ {\ sigma (1)}, b _ {\ sigma (2)}, \ ldots, b _ {\ sigma (n)} \ right)}$ ${\ displaystyle \ left (b _ {\ sigma (1)}, b _ {\ sigma (2)}, \ ldots, b _ {\ sigma (n)} \ right)}$ для некоторой перестановки $σ {\ displaystyle \ sigma}$ $\ sigma$ в симметричной группе $S n {\ displaystyle S_ {n}}$ $S_ {n}$ . Эта перестановка $σ {\ displaystyle \ sigma}$ $\ sigma$ будет называться поворотом этого скрученного n-пути и обозначаться $σ (P) {\ displaystyle \ sigma (P)}$ $\ sigma (P)$ (где P - n-путь). Это, конечно же, обобщает введенное ранее обозначение $σ (P) {\ displaystyle \ sigma (P)}$ $\ sigma (P)$ .

Вспоминая определение M, мы можем расширить det M как знаковую сумму перестановок; таким образом, получаем

det M = ∑ σ ∈ S nsign (σ) ∏ i = 1 ne (ai, b σ (i)) = ∑ σ ∈ S nsign (σ) ∏ i = 1 n ∑ P i: ai → b σ (i) ω (P i) = ∑ σ ∈ S nsign (σ) ∑ {ω (P): P n -путь от (a 1, a 2,…, an) к (b σ (1), b σ (2),…, b σ (n))} = ∑ {sign (σ (P)) ω (P): P скрученный n-путь из (a 1, a 2,…, an) к (b 1, b 2,..., bn)} = ∑ {sign (σ (P)) ω (P): P непересекающийся скрученный n -путь из (a 1, a 2,…, an) к (b 1, b 2,..., bn)} + ∑ {sign (σ (P)) ω (P): P запутанный скрученный n -путь из (a 1, a 2,…, an) to (b 1, b 2,..., bn)} = ∑ (P 1,…, P n): A → B sign (σ (P)) ω (P) + ∑ {sign (σ (P)) ω (P): P запутанный скрученный n -путь из (a 1, a 2,…, an) в (b 1, b 2,..., bn)} ⏟ = 0? {\ displaystyle {\ begin {array} {rcl} \ det M = \ sum _ {\ sigma \ in S_ {n}} \ mathrm {sign} (\ sigma) \ prod _ {i = 1} ^ {n } e (a_ {i}, b _ {\ sigma (i)}) \\ = \ sum _ {\ sigma \ in S_ {n}} \ mathrm {sign} (\ sigma) \ prod _ {i = 1} ^ {n} \ sum _ {P_ {i}: a_ {i} \ to b _ {\ sigma (i)}} \ omega (P_ {i}) \\ = \ sum _ {\ sigma \ в S_ {n}} \ mathrm {sign} (\ sigma) \ sum \ {\ omega (P): P ~ {\ text {an}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b _ {\ sigma (1)}, b _ {\ sigma (2)}, \ ldots, b _ {\ sigma (n)} \ right) \} \\ = \ sum \ {\ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {скрученный }} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \} \\ = \ sum \ {\ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {непересекающийся скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ текст {to}} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \} \\ + \ sum \ {\ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {запутанный скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n } \ right) ~ {\ text {в }} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \} \\ = \ sum _ {(P_ {1}, \ ldots, P_ {n }) \ двоеточие от A \ до B} \ mathrm {sign} (\ sigma (P)) \ omega (P) \\ + \ underbrace {\ sum \ {\ mathrm {sign} (\ sigma (P)) \ омега (P): P ~ {\ text {запутанный скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \}} _ {= 0?} \\\ end {array} }}

{\ displaystyle {\ begin {array} {rcl} \ det M = \ sum _ {\ sigma \ in S_ {n}} \ mathrm {sign} (\ sigma) \ prod _ { i = 1} ^ {n} e (a_ {i}, b _ {\ sigma (i)}) \\ = \ sum _ {\ sigma \ in S_ {n}} \ mathrm {sign} (\ sigma) \ prod _ {i = 1} ^ {n} \ sum _ {P_ {i}: a_ {i} \ to b _ {\ sigma (i)}} \ omega (P_ {i}) \\ = \ sum _ {\ sigma \ in S_ {n}} \ mathrm {sign} (\ sigma) \ sum \ {\ omega (P): P ~ {\ text {an}} ~ n {\ text {- путь от }} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b _ {\ sigma (1)}, b _ {\ sigma (2)}, \ ldots, b _ {\ sigma (n)} \ right) \} \\ = \ sum \ {\ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {к }} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \} \\ = \ sum \ { \ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {непересекающийся скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \ } \\ + \ sum \ {\ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {запутанный скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b_ {1}, b_ {2},..., b_ {n} \ right) \} \\ = \ sum _ {(P_ {1}, \ ldots, P_ {n}) \ двоеточие A \ to B} \ mathrm {sign} (\ sigma (P)) \ omega (P) \\ + \ underbrace {\ sum \ {\ mathrm {sign} (\ sigma (P)) \ omega (P): P ~ {\ text {запутанный скрученный}} ~ n {\ text {-path from}} ~ \ left (a_ {1}, a_ {2}, \ ldots, a_ {n} \ right) ~ {\ text {to}} ~ \ left (b_ {1}, b_ {2 },..., b_ {n} \ right) \}} _ {= 0?} \\\ end {array}}}

Остается показать, что сумма $знака (σ (P)) ω (P) {\ displaystyle \ mathrm {sign} (\ sigma (P)) \ omega (P)}$ ${\ Displaystyle \ mathrm {знак} (\ sigma (P)) \ omega (P)}$ по всем запутанным скрученным n-путям обращается в нуль. Пусть $E {\ displaystyle {\ mathcal {E}}}$ ${\ mathcal {E}}$ обозначает набор запутанных скрученных n-путей. Чтобы установить это, мы построим инволюцию $f: E ⟶ E {\ displaystyle f: {\ mathcal {E}} \ longrightarrow {\ mathcal {E}}}$ ${\ дис playstyle f: {\ mathcal {E}} \ longrightarrow {\ mathcal {E}}}$ со свойствами $ω (f (P)) = ω (P) {\ displaystyle \ omega (f (P)) = \ omega (P)}$ ${\ displaystyle \ omega (f (P)) = \ omega (P)}$ и $sign (σ (е (P))) знак равно - знак (σ (P)) {\ Displaystyle \ mathrm {знак} (\ sigma (f (P))) = - \ mathrm {знак} (\ sigma (P))}$ ${\ displaystyle \ mathrm {sign} (\ sigma (f (P))) = - \ mathrm {знак} (\ sigma (P))}$ для всех $P ∈ E {\ displaystyle P \ in {\ mathcal {E}}}$ ${\ displaystyle P \ in {\ mathcal {E}}}$ . При такой инволюции остаточный член в приведенной выше сумме сводится к

∑ P ∈ E sign (σ (P)) ω (P) = 1 2 (∑ P ∈ E sign (σ (P)) ω ( P) + ∑ P ∈ E sign (σ (f (P))) ω (f (P))) = 1 2 (∑ P ∈ E sign (σ (P)) ω (P) + ∑ P ∈ E - знак (σ (P)) ω (P)) = 0 {\ displaystyle {\ begin {array} {rcl} \ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma ( P)) \ omega (P) = {\ frac {1} {2}} \ left (\ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma (P)) \ omega (P) + \ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma (f (P))) \ omega (f (P)) \ right) \\ = {\ frac {1} {2}} \ left (\ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma (P)) \ omega (P) + \ sum _ {P \ in {\ mathcal {E}}} - \ mathrm {sign} (\ sigma (P)) \ omega (P) \ right) \\ = 0 \\\ end {array}}}

{\ displaystyle {\ begin {array} {rcl} \ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma (P)) \ omega (P) = {\ frac {1} {2}} \ left (\ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ si gma (P)) \ omega (P) + \ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma (f (P))) \ omega (f (P)) \ справа) \\ = {\ frac {1} {2}} \ left (\ sum _ {P \ in {\ mathcal {E}}} \ mathrm {sign} (\ sigma (P)) \ omega ( P) + \ sum _ {P \ in {\ mathcal {E}}} - \ mathrm {sign} (\ sigma (P)) \ omega (P) \ right) \\ = 0 \\\ end {массив }}}

Построение инволюции: идея, лежащая в основе определения инволюции $f {\ displaystyle f}$ $f$ , состоит в том, чтобы выбрать два пересекающихся пути внутри запутанного пути и поменять их хвостами после их точки пересечение. Обычно существует несколько пар пересекающихся путей, которые также могут пересекаться несколько раз; следовательно, необходимо сделать тщательный выбор. Пусть $P = (P 1, P 2,..., P n) {\ displaystyle P = \ left (P_ {1}, P_ {2},..., P_ {n} \ right)}$ $P = \ left (P_ {1}, P_ {2},..., P_ {n} \ right)$ - любой запутанный скрученный n-путь. Тогда $f (P) {\ displaystyle f (P)}$ $f (P)$ определяется следующим образом. Поскольку $P {\ displaystyle P}$ $P$ запутан, существует минимальный $i < j {\displaystyle i$ $i <j$ в ${1, 2,…, n} {\ displaystyle \ {1,2, \ ldots, n \}}$ $\ {1,2, \ ldots, n \}$ такие, что $P i {\ displaystyle P_ {i}}$ $P_ {i}$ и $P j {\ displaystyle P_ {j}}$ $P_ {j }$ имеют общую вершину. Выберите $i P < j P {\displaystyle i_{P}$ ${\ displaystyle i_ {P} <j_ {P}}$ как наименьший из таких индексов. Общая вершина не обязательно является конечной точкой этих путей. Обобщая эту информацию, имеем

P i ≡ ai = u 0 → u 1 → u 2… u α - 1 → u α → u α + 1… → ur = b σ (i) ⏞ taili P j ≡ aj = v 0 → v 1 → v 2… v β - 1 → v β → v β + 1… → vs = b σ (j) ⏟ tailj {\ displaystyle {\ begin {array} {rcl} P_ {i} \ Equ a_ {i} = u_ {0} \ to u_ {1} \ to u_ {2} \ ldots u _ {\ alpha -1} \ to \ overbrace {\ mathbf {u} _ {\ alpha} \ to u_ { \ alpha +1} \ ldots \ to u_ {r} = b _ {\ sigma (i)}} ^ {\ mathrm {tail} ~ i} \\ P_ {j} \ Equiv a_ {j} = v_ {0 } \ to v_ {1} \ to v_ {2} \ ldots v _ {\ beta -1} \ to \ underbrace {\ mathbf {v} _ {\ beta} \ to v _ {\ beta +1} \ ldots \ to v_ {s} = b _ {\ sigma (j)}} _ {\ mathrm {tail} ~ j} \\\ end {array}}}

{\ displaystyle {\ begin {array} {rcl} P_ {i} \ Equiv a_ {i} = u_ {0} \ to u_ {1} \ to u_ {2} \ ldots u _ {\ alpha -1} \ to \ overbrace {\ mathbf {u} _ {\ alpha} \ to u _ {\ alpha +1} \ ldots \ to u_ {r} = b _ {\ sigma (i)}} ^ {\ mathrm {tail} ~ i} \ \ P_ {j} \ Equiv a_ {j} = v_ {0} \ to v_ {1} \ to v_ {2} \ ldots v _ {\ beta -1} \ to \ underbrace {\ mathbf {v} _ { \ beta} \ to v _ {\ beta +1} \ ldots \ to v_ {s} = b _ {\ sigma (j)}} _ {\ mathrm {tail} ~ j} \\\ ru d {массив}}}

где $i = i P {\ displaystyle i = i_ {P}}$ ${\ displaystyle i = i_ {P}}$ , $j = j P {\ displaystyle j = j_ {P}}$ ${\ displaystyle j = j_ {P}}$ , $σ = σ (P) {\ displaystyle \ sigma = \ sigma (P)}$ ${\ displaystyle \ sigma = \ sigma (P)}$ и $α {\ displaystyle \ alpha}$ $\ alpha$ -я вершина вдоль $P i {\ displaystyle P_ {i}}$ $P_ {i}$ совпадает с $β {\ displaystyle \ beta}$ $\ beta$ -я вершина вдоль $P i {\ displaystyle P_ {i}}$ $P_ {i}$ . Выберите $α P, β P {\ displaystyle \ alpha _ {P}, \ beta _ {P}}$ ${\ displaystyle \ alpha _ {P}, \ beta _ {P} }$ как наименьшее возможное такое положение, конкретно $α P: = min { α ∣ ∃ β: U α знак равно v β} {\ Displaystyle \ alpha _ {P}: = \ min \ {\ alpha \ mid \ exists {\ beta: ~} u _ {\ alpha} = v _ {\ beta} \ }}$ ${\ displaystyle \ alpha _ {P}: = \ min \ {\ alpha \ mid \ exists {\ beta: ~} u _ {\ alpha} = v _ {\ beta} \}}$ и $β P: = min {β ∣ u α P = v β} {\ displaystyle \ beta _ {P}: = \ min \ {\ beta \ mid u _ {\ alpha _ {P}} = v _ {\ beta} \}}$ ${\ displaystyle \ beta _ {P}: = \ min \ {\ beta \ mid u _ {\ alpha _ {P}} = v _ {\ beta} \}}$ . Теперь установите $f (P) {\ displaystyle f (P)}$ $f (P)$ так, чтобы он совпадал с $P {\ displaystyle P}$ $P$ , за исключением компонентов $i {\ displaystyle i}$ $я$ и $j {\ displaystyle j}$ $j$ , которые заменяются на

P i ′ ≡ ai = u 0 → u 1 → u 2… u α - 1 → v β P → v β P + 1… → vs = b σ (j) ⏞ tailj P j ′ ≡ aj = v 0 → v 1 → v 2… v β - 1 → u α P → u α P + 1… → ur = б σ (я) ⏟ taili {\ displaystyle {\ begin {array} {rcl} P '_ {i} \ Equiv a_ {i} = u_ {0} \ to u_ {1} \ to u_ {2} \ ldots u _ {\ alpha -1} \ to \ overbrace {v _ {\ beta _ {P}} \ to v _ {\ beta _ {P} +1} \ ldots \ to v_ {s} = b _ {\ sigma (j)}} ^ {\ mathrm {tail} ~ j} \\ P '_ {j} \ Equiv a_ {j} = v_ {0} \ to v_ {1} \ to v_ {2 } \ ldots v _ {\ beta -1} \ to \ underbrace {u _ {\ alpha _ {P}} \ to u _ {\ alpha _ {P} +1} \ ldots \ to u_ {r} = b _ {\ sigma (i)}} _ {\ mathrm {tail} ~ i} \\\ end {array}}}

{\begin{array}{rcl}P'_{i}\equiv a_{i}=u_{0}\to u_{1}\to u_{2}\ldots u_{\alpha -1}\to \overbrace {v_{\beta _{P}}\to v_{\beta _{P}+1}\ldots \to v_{s}=b_{\sigma (j)}} ^{\mathrm {tail} ~j}\\P'_{j}\equiv a_{j}=v_{0}\to v_{1}\to v_{2}\ldots v_{\beta -1}\to \underbrace {u_{\alpha _{P}}\to u_{\alpha _{P}+1}\ldots \to u_{r}=b_{\sigma (i)}} _{\mathrm {tail} ~i}\\\end{array}}

Сразу видно, что $f (P) {\ displaystyle f (P)}$ $f (P)$ - запутанный скрученный n-путь. Пройдя этапы построения, легко увидеть, что $if (P) = i P {\ displaystyle i_ {f (P)} = i_ {P}}$ ${\ displaystyle i_ {f (P)} = i_ {P}}$ , $jf (P) = j P {\ Displaystyle j_ {f (P)} = j_ {P}}$ ${\ displaystyle j_ {f (P)} = j_ {P}}$ и, кроме того, $α f (P) = α P {\ displaystyle \ alpha _ {f (P)} = \ альфа _ {P}}$ ${\ displaystyle \ alpha _ {f (P)} = \ alpha _ {P}}$ и $β f (P) = β P {\ displaystyle \ beta _ {f (P)} = \ beta _ {P}}$ ${\ displaystyle \ beta _ {f (P)} = \ beta _ {P}}$ , так что применение $f {\ displaystyle f}$ $f$ снова к $f (P) {\ displaystyle f (P)}$ $f (P)$ включает обратную замену хвостов $f (P) i, f (P) j {\ displaystyle f (P) _ {i}, f (P) _ {j}}$ ${\ displaystyle f (P) _ {i}, f (P) _ {j}}$ и оставив другие компоненты нетронутыми. Следовательно, $f (f (P)) = P {\ displaystyle f (f (P)) = P}$ ${\ displaystyle f (f (P)) = P}$ . Таким образом, $f {\ displaystyle f}$ $f$ является инволюцией. Осталось продемонстрировать желаемые свойства антисимметрии:

Из построения видно, что $σ (f (P)) {\ displaystyle \ sigma (f (P))}$ $\ sigma (f (P))$ совпадает с $σ = σ (P) {\ displaystyle \ sigma = \ sigma (P)}$ ${\ displaystyle \ sigma = \ sigma (P)}$ , за исключением того, что меняет местами $σ (i) {\ displaystyle \ sigma (i)}$ $\ sigma (i)$ и $σ (j) {\ displaystyle \ sigma (j)}$ $\ sigma (j)$ , что дает $σ (f (P)) = - σ (P) {\ displaystyle \ sigma (f (P)) = - \ sigma (P)}$ ${\ displaystyle \ sigma (f (P)) = - \ sigma (P)}$ . Чтобы показать, что $ω (f (P)) = ω (P) {\ displaystyle \ omega (f (P)) = \ omega (P)}$ ${\ displaystyle \ omega (f (P)) = \ omega (P)}$ , мы сначала вычисляем, обращаясь к хвосту -замена

ω (P i ′) ω (P j ′) = (∏ t = 0 α - 1 ω (ut, ut + 1) ⋅ ∏ t = β s - 1 ω (vt, vt + 1)) ⋅ (∏ t = 0 β - 1 ω (vt, vt + 1) ⋅ ∏ t = α r - 1 ω (ut, ut + 1)) = ∏ t = 0 r - 1 ω (ut, ut + 1) ⋅ ∏ t = 0 s - 1 ω (vt, vt + 1) = ω (P i) ω (P j). {\ displaystyle {\ begin {array} {rcl} \ omega (P '_ {i}) \ omega (P' _ {j}) = \ left (\ prod _ {t = 0} ^ {\ alpha -1} \ omega (u_ {t}, u_ {t + 1}) \ cdot \ prod _ {t = \ beta} ^ {s-1} \ omega (v_ {t}, v_ {t + 1}) \ right) \ cdot \ left (\ prod _ {t = 0} ^ {\ beta -1} \ omega (v_ {t}, v_ {t + 1}) \ cdot \ prod _ {t = \ alpha} ^ {r-1} \ omega (u_ {t}, u_ {t + 1}) \ right) \\ = \ prod _ {t = 0} ^ {r-1} \ omega (u_ {t}, u_ {t + 1}) \ cdot \ prod _ {t = 0} ^ {s-1} \ omega (v_ {t}, v_ {t + 1}) \\ = \ omega (P_ {i}) \ omega (P_ {j}). \\\ end {array}}}

{\begin{array}{rcl}\omega (P'_{i})\omega (P'_{j})=\left(\prod _{t=0}^{\alpha -1}\omega (u_{t},u_{t+1})\cdot \prod _{t=\beta }^{s-1}\omega (v_{t},v_{t+1})\right)\cdot \left(\prod _{t=0}^{\beta -1}\omega (v_{t},v_{t+1})\cdot \prod _{t=\alpha }^{r-1}\omega (u_{t},u_{t+1})\right)\\=\prod _{t=0}^{r-1}\omega (u_{t},u_{t+1})\cdot \prod _{t=0}^{s-1}\omega (v_{t},v_{t+1})\\=\omega (P_{i})\omega (P_{j}).\\\end{array}}

Следовательно, $ω (f (P)) = ∏ k = 1 n ω (f (P) k) = ∏ k = 1, k ≠ i, jn ω (P k) ⋅ ω (P i ′) ω (P j ′) = ∏ k = 1, k ≠ i, jn ω (P k) ⋅ ω (P i) ω ( П j) знак равно ∏ К знак равно 1 N ω (п К) знак равно ω (P) {\ Displaystyle \ omega (f (P)) = \ prod _ {k = 1} ^ {n} \ omega (f (P) _ {k}) = \ prod _ {k = 1, ~ k \ neq i, j} ^ {n} \ omega (P_ {k}) \ cdot \ omega (P '_ {i}) \ omega (P '_ {j}) = \ prod _ {k = 1, ~ k \ neq i, j} ^ {n} \ omega (P_ {k}) \ cdot \ omega (P_ {i}) \ omega (P_ { j}) = \ prod _ {k = 1} ^ {n} \ omega (P_ {k}) = \ omega (P)}$ $\omega (f(P))=\prod _{k=1}^{n}\omega (f(P)_{k})=\prod _{k=1,~k\neq i,j}^{n}\omega (P_{k})\cdot \omega (P'_{i})\omega (P'_{j})=\prod _{k=1,~k\neq i,j}^{n}\omega (P_{k})\cdot \omega (P_{i})\omega (P_{j})=\prod _{k=1}^{n}\omega (P_{k})=\omega (P)$ .

Таким образом, мы нашли инволюцию с желаемыми свойствами и завершили доказательство Линд Лемма Стрёма-Гесселя-Виенно.

Замечание. Аргументы, аналогичные приведенному выше, встречаются в нескольких источниках с вариациями относительно выбора того, какой хвост переключить. Версия с j наименьшим (не равным i), а не наибольшим, появляется в ссылке Gessel-Viennot 1989 (доказательство теоремы 1).

Приложения

Многочлены Шура

Лемма Линдстрема – Гесселя – Венно может использоваться для доказательства эквивалентности следующих двух различных определений многочленов Шура. Дано разбиение $λ = λ 1 + ⋯ + λ r {\ displaystyle \ lambda = \ lambda _ {1} + \ cdots + \ lambda _ {r}}$ $\ lambda = \ lambda _ {1} + \ cdots + \ lambda _ {r}$ числа n, многочлен Шура $s λ (x 1,…, xn) {\ displaystyle s _ {\ lambda} (x_ {1}, \ ldots, x_ {n})}$ $s _ {\ lambda} ( x_ {1}, \ ldots, x_ {n})$ можно определить как:

$s λ (Икс 1,…, Xn) знак равно ∑ T вес (T), {\ Displaystyle s _ {\ lambda} (x_ {1}, \ ldots, x_ {n}) = \ sum _ {T} w (T),}$ $s _ {\ lambda} (x_ {1}, \ ldots, x_ {n}) = \ sum _ {T} w (T),$

где сумма берется по всем полустандартным таблицам Юнга T формы λ, а вес таблицы T определяется как моном, полученный произведением x i, индексированных записи i из T. Например, вес таблицы 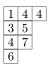равен $x 1 x 3 x 4 3 x 5 x 6 x 7 {\ displaystyle x_ {1} x_ {3} x_ {4} ^ { 3} x_ {5} x_ {6} x_ {7}}$ $x_ {1} x_ {3} x_ {4} ^ {3} x_ {5} x_ {6} x_ {7}$ .

$s λ (x 1,…, xn) = det ((h λ i + j - i) i, jr × r), {\ displaystyle s _ {\ lambda} (x_ {1}, \ ldots, x_ {n}) = \ det \ left ((h _ {\ lambda _ {i} + ji}) _ {i, j} ^ {r \ times r } \ right),}$ $s_ { \ lambda} (x_ {1}, \ ldots, x_ {n}) = \ det \ left ((h _ {{\ lambda _ {i} + ji}}) _ {{i, j}} ^ {{r \ times r}} \ right),$

где h i - это полные однородные симметричные многочлены (с h i, понимаемым как 0, если i отрицательно ive). Например, для разбиения (3,2,2,1) соответствующий определитель равен

s (3, 2, 2, 1) = | ч 3 ч 4 ч 5 ч 6 ч 1 ч 2 ч 3 ч 4 1 ч 1 ч 2 ч 3 0 0 1 ч 1 |. {\ displaystyle s _ {(3,2,2,1)} = {\ begin {vmatrix} h_ {3} h_ {4} h_ {5} h_ {6} \\ h_ {1} h_ {2} h_ { 3} h_ {4} \\ 1 h_ {1} h_ {2} h_ {3} \\ 0 0 1 h_ {1} \ end {vmatrix}}.}

s _ {{(3,2,2,1)}} = {\ begin {vmatrix} h_ {3} h_ {4} h_ {5} h_ {6 } \\ h_ {1} h_ {2} h_ {3} h_ {4} \\ 1 h_ {1} h_ {2} h_ {3} \\ 0 0 1 h_ {1} \ end {vmatrix}}.

Чтобы доказать эквивалентность, для любого разбиения λ, как указано выше, один рассматривает r начальных точек $ai = (r + 1 - i, 1) {\ displaystyle a_ {i} = (r + 1-i, 1)}$ $a_{i}=(r+1-i,1)$ и r конечных точек $bi = (λ i + r + 1 - i, n) {\ displaystyle b_ {i} = (\ lambda _ {i} + r + 1-i, n)}$ $b_ {i} знак равно (\ лямбда _ {я} + г + 1-я, п)$ , как точки в решетка $Z 2 {\ displaystyle \ mathbb {Z} ^ {2}}$ ${\ mathbb {Z}} ^ {2}$ , которая приобретает структуру ориентированного графа, утверждая, что единственные разрешенные направления - один вправо или один вверх; вес, связанный с любым горизонтальным ребром на высоте i, равен x i, а вес, связанный с вертикальным ребром, равен 1. С этим определением r-наборы путей от A до B являются в точности полустандартными таблицами Юнга shape λ, и вес такого r-набора является соответствующим слагаемым в первом определении полиномов Шура. Например, с таблицей получается соответствующий 4-кортеж

. С другой стороны, матрица M в точности совпадает с матрицей, записанной выше для D. Это показывает требуемую эквивалентность. (См. Также §4.5 в книге Сагана, или Первое доказательство теоремы 7.16.1 в EC2 Стэнли, или §3.3 в препринте Фулмека arXiv, или §9.13 в примечаниях к лекции Мартина, для небольших вариаций этого аргумента.)

Формула Коши – Бине

Можно также использовать лемму Линдстрема – Гесселя – Венно для доказательства формулы Коши – Бине и, в частности, мультипликативности определителя.

Обобщения

Формула Таласки

Ацикличность G - существенное предположение леммы Линдстрема – Гесселя – Виенно; он гарантирует (в разумных ситуациях), что суммы $e (a, b) {\ displaystyle e (a, b)}$ $e(a,b)$ правильно определены, и он входит в доказательство (если G не ациклично, тогда f может преобразовать самопересечение пути в пересечение двух различных путей, что нарушает аргумент, что f является инволюцией). Тем не менее, статья Келли Таласка 2012 года устанавливает формулу, обобщающую лемму на произвольные орграфы. Суммы $e (a, b) {\ displaystyle e (a, b)}$ $e(a,b)$ заменяются формальным степенным рядом, а сумма по непересекающимся кортежам путей теперь становится суммой по совокупностям непересекающихся и несамопересекающиеся пути и циклы, разделенные на сумму по совокупности непересекающихся циклов. За подробностями отсылаем читателя к статье Таласки.

См. Также

Теорема о матричном дереве

Ссылки

Гессель, Ира М. ; (1989), Детерминанты, пути и плоские разделы (PDF)
Саган, Брюс Э. (2001), Симметричная группа, Спрингер
Стэнли, Ричард П. (1999), Перечислительная комбинаторика, том 2, CUP
Таласка, Келли (2012), Детерминанты взвешенных матриц путей, arXiv : 1202.3128v1
Мартин, Джереми (2012), Конспект лекций по алгебраической комбинаторике (PDF)
Фулмек, Маркус (2010), Рассмотрение детерминантов как непересекающихся решетчатых путей дает биективные классические детерминантные тождества, arXiv : 1010.3860v1