Структура данных с несвязанным набором

редактировать

Лес с несвязным набором / объединением-поиском

Тип

многостороннее дерево

Изобретено

1964

Изобретен

Бернардом А. Галлером и Майклом Дж. Фишером

Сложность времени в нотации большой O

Алгоритм	Среднее	Худший вариант
Пробел	O (n)	O (n)
Поиск	O (α (n))	O (α ( n))
Объединить	O (α (n))	O (α (n))

MakeSet создает 8 синглтонов.

После некоторых операций Union некоторые наборы становятся сгруппированы вместе.

В информатике, структура данных с непересекающимися наборами, также называемая объединением – поиск структурой данных или объединением – поиском set - это структура данных, в которой хранится набор непересекающихся (неперекрывающихся) наборов. Эквивалентно, он хранит раздел набора на непересекающиеся подмножества. Он предоставляет операции для добавления новых наборов, слияния наборов (замены их их union ) и поиска представительного члена набора. Последняя операция позволяет оперативно узнать, находятся ли какие-либо два элемента в одном или разных наборах.

Хотя существует несколько способов реализации структур данных с непересекающимися наборами, на практике они часто отождествляются с конкретной реализацией, называемой лесом с непересекающимися наборами . Это специализированный тип леса, который выполняет объединение и находку почти с постоянным амортизированным временем. Чтобы выполнить последовательность из m операций сложения, объединения или поиска в лесу с непересекающимися множествами с n узлами, требуется общее время O (mα (n)), где α (n) - чрезвычайно медленно растущая обратная функция Аккермана.. Леса с непересекающимися наборами не гарантируют такую производительность для каждой операции. Отдельные операции объединения и поиска могут занимать больше времени, чем постоянное время, умноженное на α (n), но каждая операция заставляет лес непересекающихся множеств настраиваться так, чтобы последующие операции выполнялись быстрее. Непересекающиеся леса являются асимптотически оптимальными и практически эффективными.

Непересекающиеся структуры данных играют ключевую роль в алгоритме Крускала для поиска минимального остовного дерева графа. Важность минимальных остовных деревьев означает, что структуры данных с непересекающимся набором данных лежат в основе широкого разнообразия алгоритмов. Кроме того, структуры данных с непересекающимся набором также имеют приложения для символьных вычислений, а также в компиляторах, особенно для задач распределения регистров.

Содержание

1 История
2 Представление
3 Операции
- 3.1 Создание новых наборов
- 3.2 Поиск представителей множества
- 3.3 Объединение двух наборов
4 Временная сложность
- 4.1 Доказательство сложности времени O (log * (n)) Union-Find
5 Applications
6 См. Также
7 Ссылки
8 Внешние ссылки

История

Disjoint- множественные леса были впервые описаны Бернардом А. Галлером и Майклом Дж. Фишером в 1964 году. В 1973 году их временная сложность была ограничена $O (log ∗ ⁡ (n)) {\ displaystyle O (\ log ^ {*} (n))}$ ${\ displaystyle O (\ log ^ {*} (n))}$ , повторный логарифм числа $n {\ displaystyle n}$ $n$ , Авторы Хопкрофт и Уллман. (Доказательство доступно здесь.) В 1975 году Роберт Тарджан первым доказал $O (m α (n)) {\ displaystyle O (m \ alpha (n))}$ ${\ displaystyle O (m \ alpha (n))}$ (обратная функция Аккермана ) верхняя граница временной сложности алгоритма и в 1979 году показала, что это была нижняя граница для ограниченного случая. В 1989 г. Фредман и Сакс показали, что $Ω (α (n)) {\ displaystyle \ Omega (\ alpha (n))}$ $\ Omega (\ alpha ( n))$ ( амортизированные) слова должны быть доступны любой структуре данных с непересекающимся набором для каждой операции, тем самым доказывая оптимальность структуры данных.

В 1991 году Galil и Italiano опубликовали обзор структур данных для непересекающихся множеств.

В 1994 году Ричард Дж. Андерсон и Хизер Уолл описали параллельную версию Union-Find, которая никогда не нуждается в для блокировки.

В 2007 году Сильвен Коншон и Жан-Кристоф Филлиатр разработали постоянную версию структуры данных с непересекающимся набором данных, позволяющую эффективно сохранять предыдущие версии структуры и формализовала его правильность с помощью помощника по проверке Coq. Однако реализация является асимптотической только в том случае, если используется эфемерно или если одна и та же версия структуры используется повторно с ограниченным поиском с возвратом.

Представление

Каждый узел в лесу непересекающихся множеств состоит из указателя и некоторой вспомогательной информации, либо размера, либо ранга (но не обоих сразу). Указатели используются для создания родительских деревьев указателей, где каждый узел, не являющийся корнем дерева, указывает на своего родителя. Чтобы отличать корневые узлы от других, их родительские указатели имеют недопустимые значения, такие как циклическая ссылка на узел или контрольное значение. Каждое дерево представляет собой набор, хранящийся в лесу, причем элементы набора являются узлами в дереве. Корневые узлы предоставляют представителей множества: два узла находятся в одном наборе тогда и только тогда, когда корни деревьев, содержащих узлы, равны.

Узлы в лесу можно хранить любым удобным для приложения способом, но обычно их хранят в массиве. В этом случае родители могут быть обозначены индексом их массива. Для каждой записи массива требуется как минимум O (lg n) бит памяти для родительского указателя. Для остальной части записи требуется сопоставимый или меньший объем памяти, поэтому количество битов, необходимых для хранения леса, равно O (n lg n). Если реализация использует узлы фиксированного размера (тем самым ограничивая максимальный размер леса, который может быть сохранен), то необходимое хранилище линейно по n.

Операции

Структуры данных с непересекающимся набором поддерживают три операции: создание нового набора, содержащего новый элемент, поиск представителя набора, содержащего данный элемент, и слияние двух наборов.

Создание новых наборов

Операция MakeSet добавляет новый элемент. Этот элемент помещается в новый набор, содержащий только новый элемент, и новый набор добавляется в структуру данных. Если вместо этого структура данных рассматривается как раздел набора, то операция MakeSet увеличивает набор, добавляя новый элемент, и расширяет существующий раздел, помещая новый элемент в новое подмножество, содержащее только новый элемент.

В непересекающемся лесу MakeSet инициализирует родительский указатель узла и размер или ранг узла. Если корень представлен узлом, который указывает на себя, то добавление элемента можно описать с помощью следующего псевдокода:

function MakeSet (x) isifx еще не в лесу тогда x.parent: = x x.size: = 1 // если узлы хранят размер x.rank: = 0 // если узлы хранят ранг end if end function

This операция имеет постоянную временную сложность. В частности, инициализация леса непересекающихся множеств с n узлами требует времени O (n).

На практике MakeSet должна предшествовать операция, которая выделяет память для хранения x. Пока выделение памяти является амортизированной операцией с постоянным временем, как и в случае хорошей реализации динамического массива, оно не меняет асимптотическую производительность леса случайного набора.

Поиск представителей множества

Операция поиска следует по цепочке родительских указателей от указанного узла запроса x до тех пор, пока не достигнет корневого элемента. Этот корневой элемент представляет собой набор, которому принадлежит x, и может быть самим x. Find возвращает корневой элемент, которого он достигает.

Выполнение операции поиска представляет собой важную возможность для улучшения леса. Время в операции поиска тратится на погоню за родительскими указателями, поэтому более плоское дерево приводит к более быстрым операциям поиска. Когда выполняется поиск, нет более быстрого способа достичь корня, чем последовательное отслеживание каждого родительского указателя. Однако родительские указатели, посещенные во время этого поиска, могут быть обновлены, чтобы они указывали ближе к корню. Поскольку каждый элемент, посещаемый на пути к корню, является частью одного и того же набора, это не меняет наборы, хранящиеся в лесу. Но это ускоряет будущие операции поиска не только для узлов между узлом запроса и корнем, но и для их потомков. Это обновление является важной частью гарантии амортизированной производительности несвязанного леса.

Существует несколько алгоритмов поиска, которые достигают асимптотически оптимальной временной сложности. Одно семейство алгоритмов, известное как сжатие пути, делает каждый узел между узлом запроса и корнем точкой к корню. Сжатие пути может быть реализовано с помощью простой рекурсии следующим образом:

function Find (x) isifx.parent ≠ x then x.parent: = Find (x.parent) return x.parent elsereturn x end if end function

Эта реализация выполняет два прохода, один вверх по дереву и один отступил. Требуется достаточно оперативной памяти для хранения пути от узла запроса к корню (в приведенном выше псевдокоде путь неявно представлен с помощью стека вызовов). Его можно уменьшить до постоянного объема памяти, выполняя оба прохода в одном направлении. Реализация постоянной памяти проходит от узла запроса к корню дважды, один раз для поиска корня и один раз для обновления указателей:

function Find (x) is root: = x в то время как root.parent ≠ root do root: = root.parent end while while x.parent ≠ root do parent : = x.parent x.parent: = root x: = parent end while return root end function

Tarjan and Van Leeuwen также разработали однопроходные алгоритмы поиска, которые сохраняют ту же сложность наихудшего случая, но более эффективны на практике. Это называется разделением пути и делением пути пополам. Оба они обновляют родительские указатели узлов на пути между узлом запроса и корнем. Разделение пути заменяет каждый родительский указатель на этом пути указателем на прародителя узла:

function Find (x) iswhile x.parent ≠ x do (x, x.parent): = (x.parent, x.parent.parent) end while return x end function

Деление пути вдвое работает аналогично, но заменяет только все остальные родительские указатели:

function Find (x) iswhile x.parent ≠ x do x.parent: = x.parent.parent x: = x.parent end while return x end function

Объединение двух наборов

Операция Union (x, y) заменяет набор, содержащий x, и набор, содержащий y, с их объединением. Сначала Union использует Find для определения корней деревьев, содержащих x и y. Если корни одинаковые, делать больше нечего. В противном случае два дерева необходимо объединить. Это делается либо путем установки родительского указателя x на y, либо путем установки родительского указателя y на x.

Выбор узла, который станет родительским, имеет последствия для сложности будущих операций с деревом. Если это сделать неаккуратно, деревья могут стать чрезмерно высокими. Например, предположим, что Union всегда делал дерево, содержащее x, поддеревом дерева, содержащего y. Начните с леса, который только что был инициализирован элементами 1, 2, 3,..., n, и выполните Union (1, 2), Union (2, 3),..., Union (n - 1, n). Результирующий лес содержит одно дерево с корнем n, а путь от 1 до n проходит через каждый узел в дереве. Для этого леса время выполнения Find (1) составляет O (n).

В эффективной реализации высота дерева управляется с помощью объединения по размеру или объединения по рангу . Оба они требуют, чтобы узел хранил информацию помимо своего родительского указателя. Эта информация используется, чтобы решить, какой корень станет новым родителем. Обе стратегии гарантируют, что деревья не станут слишком глубокими.

В случае объединения по размеру узел сохраняет свой размер, который представляет собой просто количество его потомков (включая сам узел). Когда деревья с корнями x и y объединяются, узел с большим количеством потомков становится родителем. Если два узла имеют одинаковое количество потомков, то любой из них может стать родительским. В обоих случаях размер нового родительского узла устанавливается равным новому общему числу потомков.

function Union (x, y) is // Заменим узлы корнями x: = Find (x) y: = Find (y) if x = y thenreturn // x и y уже находятся в одном наборе end if // Если необходимо, переименуйте переменные, чтобы // x имел не менее много потомков как y if x.size < y.size then (x, y): = (y, x) end if // Сделайте x новым корнем y. parent: = x // Обновляем размер x x.size: = x.size + y.size end function

Количество битов, необходимых для сохранения размера, явно равно количеству битов, необходимых для хранения n. Это добавляет постоянный коэффициент к требуемому хранилищу леса.

Для объединения по рангу узел сохраняет свой ранг, который является верхней границей его высоты. Когда узел инициализируется, его ранг устанавливается на ноль. Чтобы объединить деревья с корнями x и y, сначала сравните их ранги. Если ранги различны, то большее дерево рангов становится родительским, и ранги x и y не меняются. Если ранги одинаковы, то любой из них может стать родителем, но ранг нового родителя увеличивается на единицу. Хотя ранг узла явно связан с его высотой, хранение рангов более эффективно, чем сохранение высот. Высота узла может измениться во время операции поиска, поэтому сохранение рангов позволяет избежать дополнительных усилий по поддержанию правильной высоты. В псевдокоде объединение по рангу:

function Union (x, y) is // Заменить узлы корнями x: = Find (x) y: = Find (y) if x = y thenreturn // x и y уже находятся в одном наборе end if // Если необходимо, переименуйте переменные, чтобы гарантировать что // x имеет ранг не меньше, чем y if x.rank < y.rank then (x, y): = (y, x) end if // Делаем x новым корнем y.parent: = x // При необходимости увеличиваем ранг x, если x.rank = y.rank, то x.rank: = x.rank + 1 end if end function

Можно показать, что каждый узел имеет ранг ⌊lg n⌋ или меньше. Следовательно, ранг может храниться в O (log log n) битах, что делает его асимптотически незначительной частью размера леса.

Из приведенных выше реализаций ясно, что размер и ранг узла не имеют значения, если только узел не является корнем дерева. Как только узел становится дочерним, его размер и ранг больше не доступны.

Сложность времени

Реализация леса с непересекающимся набором, в которой Find не обновляет родительские указатели и в которой Union не пытается управлять высотой дерева, может иметь деревья с высотой O (n). В такой ситуации операции Find и Union требуют времени O (n).

Если реализация использует только сжатие пути, то последовательность из n операций MakeSet, за которыми следуют до n - 1 операций объединения и f операций поиска, имеет время выполнения в наихудшем случае $Θ (n + е ⋅ (1 + журнал 2 + f / n ⁡ n)) {\ displaystyle \ Theta (n + f \ cdot (1+ \ log _ {2 + f / n} n))}$ ${\ displaystyle \ Theta (n + f \ cdot (1+ \ log _ {2 + f / n} n))}$ .

Использование объединения по rank, но без обновления родительских указателей во время поиска, дает время выполнения $Θ (m lg ⁡ n) {\ displaystyle \ Theta (m \ lg n)}$ ${\ displaystyle \ Theta (m \ lg n)}$ для m операций любого типа, до n из них являются операциями MakeSet.

Комбинация сжатия пути, разделения или деления пополам с объединением по размеру или рангу сокращает время выполнения m операций любого типа, до n из которых являются операциями MakeSet для $Θ (m α (n)) {\ displaystyle \ Theta (m \ alpha (n))}$ ${\ displaystyle \ Theta (m \ alpha (n))}$ . Это делает амортизированным временем выполнения каждой операции $Θ (α (n)) {\ displaystyle \ Theta (\ alpha (n))}$ ${\ displaystyle \ Theta (\ alpha (n))}$ . Это асимптотически оптимально, что означает, что каждая структура данных непересекающегося набора должна использовать $Ω (α (n)) {\ displaystyle \ Omega (\ alpha (n))}$ $\ Omega (\ alpha ( n))$ амортизированное время на операцию. Здесь функция $α (n) {\ displaystyle \ alpha (n)}$ $\ alpha (n)$ - это обратная функция Аккермана. Обратная функция Аккермана растет чрезвычайно медленно, поэтому этот коэффициент равен 4 или меньше для любого n, которое действительно может быть записано в физической вселенной. Это делает операции с непересекающимися множествами практически постоянными по времени.

Доказательство временной сложности O (log * (n)) Union-Find

Точный анализ производительности леса непересекающихся множеств довольно сложен. Однако существует гораздо более простой анализ, который доказывает, что амортизированное время для любых m операций поиска или объединения в лесу с непересекающимися множествами, содержащем n объектов, равно O (log n), где log обозначает повторный логарифм.

Лемма 1: Поскольку функция find следует по пути к корню, ранг узла, с которым она сталкивается, увеличивается.

Доказательство: утверждают, что, поскольку к набору данных применяются операции Find и Union, этот факт остается верным с течением времени. Изначально, когда каждый узел является корнем своего собственного дерева, это тривиально верно. Единственный случай, когда ранг узла может быть изменен, - это когда применяется операция Объединение по рангу. В этом случае дерево с меньшим рангом будет прикреплено к дереву с большим рангом, а не наоборот. И во время операции поиска все узлы, посещенные по пути, будут привязаны к корню, который имеет больший ранг, чем его дочерние элементы, поэтому эта операция также не изменит этот факт.

Лемма 2: Узел u, который является корневым поддерева ранга r имеет не менее 2 узлов.

Доказательство: изначально, когда каждый узел является корнем своего собственного дерева, это тривиально верно. Предположим, что узел u ранга r имеет не менее 2 узлов. Затем, когда два дерева с рангом r объединяются по рангу и образуют дерево с рангом r + 1, новый узел имеет не менее 2 + 2 = 2 узла.

Лемма 3: Максимальное количество узлов ранга r не превосходит n / 2.

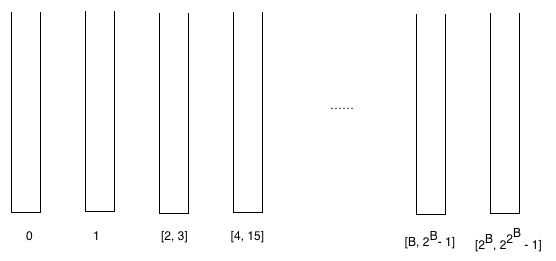
Доказательство: из леммы 2 мы знаем, что узел u, который является корнем поддерева с рангом r, имеет как минимум 2 узла. Мы получим максимальное количество узлов ранга r, когда каждый узел ранга r является корнем дерева, которое имеет ровно 2 узла. В этом случае количество узлов ранга r равно n / 2

Для удобства мы определяем здесь «ведро»: ведро - это набор, содержащий вершины с определенными рангами.

Мы создаем несколько корзин и индуктивно помещаем в них вершины в соответствии с их рангами. То есть вершины с рангом 0 попадают в нулевое ведро, вершины с рангом 1 попадают в первое ведро, вершины с рангом 2 и 3 - во второе ведро. Если B-й блок содержит вершины с рангами из интервала [r, 2 - 1] = [r, R - 1], то (B + 1) -ое ведро будет содержать вершины с рангами из интервала [R, 2 - 1].

Доказательство

O (log ∗ ⁡ n) {\ displaystyle O (\ log ^ {*} n)}

{\ displaystyle O (\ log ^ {*} n)}

Union Find

Мы можем сделать два наблюдения относительно корзин.

Общее количество сегментов не превышает logn
Доказательство: когда мы переходим от одного ведра к другому, мы добавляем еще два к мощности, то есть следующее ведро к [B, 2 - 1] будет [2, 2 - 1]
Максимальное количество элементов в сегменте [B, 2 - 1] не более 2n / 2
Доказательство: максимальное количество элементов в сегменте [B, 2 - 1] не более n / 2 + n / 2 + n / 2 +… + n / 2 ≤ 2n / 2

Пусть F представляет список выполненных операций "найти", и пусть

T 1 = ∑ F (ссылка на корень) {\ displaystyle T_ {1} = \ sum _ {F} {\ text {(ссылка на корень)}}}

T_1 = \ sum_F \ text {(ссылка на корень)}

T 2 = ∑ F (количество ссылки, пройденные там, где сегменты разные) {\ displaystyle T_ {2} = \ sum _ {F} {\ text {(количество пройденных ссылок, где сегменты разные)}}}

T_2 = \ sum_F \ text {( количество пройденных ссылок в разных сегментах)}

T 3 = ∑ F (количество ссылок, пройденных там, где сегменты совпадают). {\ displaystyle T_ {3} = \ sum _ {F} {\ text {(количество пройденных ссылок, где сегменты совпадают).}}}

T_3 = \ sum_F \ text {(количество пройденных ссылок, где сегменты совпадают).}

Тогда общая стоимость m найденных результатов составит T = T 1 + T 2 + T 3

Поскольку каждая операция поиска выполняет ровно один обход, ведущий к корню, мы имеем T 1 = O (m).

Кроме того, исходя из приведенной выше границы количества сегментов, мы имеем T 2 = O (mlogn).

Для T 3, предположим, что мы пересекаем ребро от u до v, где u и v имеют ранг в сегменте [B, 2 - 1], а v не является корнем ( во время этого обхода, в противном случае обход был бы учтен в T 1). Зафиксируем u и рассмотрим последовательность v 1,v2,..., v k, которые играют роль v в различных операциях поиска. Из-за сжатия пути и без учета ребра к корню эта последовательность содержит только разные узлы, а из леммы 1 мы знаем, что ранги узлов в этой последовательности строго возрастают. Поскольку оба узла находятся в ведре, мы можем заключить, что длина последовательности k (количество раз, когда узел u присоединяется к другому корню в одном и том же ведре) не превышает количества рангов в ведрах B, т. Е. не более 2 - 1 - B < 2.

Следовательно, $T 3 ≤ ∑ [B, 2 B - 1] ∑ u 2 B. {\ displaystyle T_ {3} \ leq \ sum _ {[B, 2 ^ {B} -1]} \ sum _ {u} 2 ^ {B}.}$ ${\ displaystyle T_ {3} \ leq \ sum _ {[B, 2 ^ {B} -1]} \ sum _ {u} 2 ^ {B}.}$

Из наблюдений 1 и 2, мы можем заключить, что $T 3 ≤ B 2 B 2 n 2 B ≤ 2 n log ∗ ⁡ n. {\ displaystyle T_ {3} \ leq \ sum _ {B} 2 ^ {B} {\ frac {2n} {2 ^ {B}}} \ leq 2n \ log ^ {*} n.}$ $T_3 \ le \ sum_ {B} 2 ^ B \ frac {2n} {2 ^ B} \ le 2n \ log ^ * n.$

Следовательно, T = T 1 + T 2 + T 3 = O (m logn).

Приложения

Демонстрация для Union-Find при использовании алгоритма Крускала для поиска минимального связующего дерева.

Структуры данных с непересекающимися наборами моделируют разбиение набора, например, для отслеживать связанные компоненты неориентированного графа . Затем эту модель можно использовать, чтобы определить, принадлежат ли две вершины одному и тому же компоненту, или добавление ребра между ними приведет к возникновению цикла. Алгоритм объединения-поиска используется в высокопроизводительных реализациях унификации.

. Эта структура данных используется Библиотекой графов ускорения для реализации своих функций Инкрементальные подключенные компоненты. Это также ключевой компонент в реализации алгоритма Крускала для поиска минимального остовного дерева графа.

Обратите внимание, что реализация в виде непересекающихся лесов не позволяет удалять ребра даже без сжатия пути или эвристики ранга.

Шарир и Агарвал сообщают о связи между наихудшим поведением непересекающихся множеств и длиной последовательностей Давенпорта – Шинцеля, комбинаторной структуры из вычислительной геометрии.

См. также

Уточнение разделения, другая структура данных для поддержания непересекающихся наборов, с обновлениями, которые разделяют наборы, а не объединяют их вместе
Динамическое соединение

Ссылки

Внешние ссылки

Реализация C ++, часть библиотек Boost C ++
Реализация Java с приложением для сегментации цветных изображений, Статистическое слияние областей (SRM), IEEE Trans. Pattern Anal. Мах. Intell. 26 (11): 1452–1458 (2004)
Java-апплет: графическое объединение - реализация поиска, Рори Л.П. Макгуайр
Реализация Matlab, которая является частью
реализации Python
Наглядное объяснение и код C #