Угловое смещение

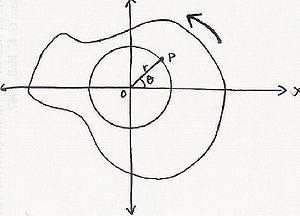
Вращение твердого тела P вокруг фиксированной оси O.

Угловое смещение тела - это угол в радианах (градусов, оборотов ), через который точка вращается вокруг центра или линия была повернута в определенном смысле относительно указанной оси . Когда тело вращается вокруг своей оси, движение нельзя просто анализировать как частицу, поскольку при круговом движении оно претерпевает изменяющуюся скорость и ускорение в любой момент времени (t). Когда речь идет о вращении тела, становится проще считать само тело твердым. Тело обычно считается твердым, когда расстояние между всеми частицами остается постоянным на протяжении всего движения тела, например, части его массы не разлетаются. В реальном смысле все может быть деформируемым, однако это воздействие минимально и незначительно. Таким образом, вращение твердого тела над фиксированной осью называется вращательным движением.

• 1 Пример
• 2 Измерения
• 3 Трехмерные
  • 3.1 Матричные обозначения
• 4 Матрицы бесконечно малых вращений
  • 4.1 Генераторы вращений
  • 4.2 Связь с алгебрами Ли
  • 4.3 Экспоненциальное отображение
• 5 См. Также
• 6 Ссылки

В примере, показанном на справа (или выше в некоторых мобильных версиях) частица или тело P находится на фиксированном расстоянии r от начала координат O, вращаясь против часовой стрелки. Затем становится важным представить положение частицы P в терминах ее полярных координат (r, θ). В этом конкретном примере значение θ изменяется, а значение радиуса остается прежним. (В прямоугольных координатах (x, y) и x, и y меняются со временем). Когда частица движется по окружности, она проходит длину дуги s, которая становится связанной с угловым положением через соотношение: -

$s\; =\; r\; \theta \; \{\backslash \; displaystyle\; s\; =\; r\; \backslash \; theta\; \backslash ,\; \}$

Угловое смещение может быть измерено в радианах или градусах. Использование радианов обеспечивает очень простую связь между расстоянием, пройденным по окружности, и расстоянием r от центра.

$\theta \; =\; sr\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{s\}\; \{r\}\}\}$

Например, если тело вращается на 360 ° по окружности радиуса r, угловое смещение определяется расстоянием прошел по окружности, равной 2πr, деленной на радиус: $\theta \; =\; 2\; \pi \; rr\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{2\; \backslash \; pi\; r\}\; \{r\}\}\}$что легко упрощается до: $\theta \; =\; 2\; \pi \; \{\backslash \; displaystyle\; \backslash \; theta\; =\; 2\; \backslash \; pi\}$. Следовательно, 1 оборот равен $2\; \pi \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\}$радиан.

Когда частица перемещается из точки P в точку Q за $\delta \; t\; \{\backslash \; displaystyle\; \backslash \; delta\; t\}$, как на иллюстрации слева, радиус круг проходит через изменение угла $\Delta \; \theta \; =\; \theta \; 2\; -\; \theta \; 1\; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; theta\; =\; \backslash \; theta\; \_\; \{2\}\; -\; \backslash \; theta\; \_\; \{1\}\}$, что равно угловому смещение.

Рисунок 1 : теорема Эйлера о вращении. Большой круг при вращении превращается в другой большой круг, всегда оставляя диаметр сферы в исходном положении. Рисунок 2 : Вращение, представленное осью Эйлера и углом.

В трех измерениях, угловой смещение - это сущность с направлением и величиной. Направление определяет ось вращения, которая всегда существует в силу теоремы вращения Эйлера ; величина определяет вращение в радианах вокруг этой оси (используя правило правой руки для определения направления). Этот объект называется ось-угол.

. Несмотря на направление и величину, угловое смещение не является вектором , потому что оно не подчиняется закону коммутативности для сложения. Тем не менее, имея дело с бесконечно малыми вращениями, бесконечно малые величины второго порядка можно отбросить, и в этом случае появляется коммутативность.

Существует несколько способов описания углового смещения, таких как матрицы вращения или углы Эйлера. См. Диаграммы на SO (3) для других.

Матричная запись

Учитывая, что любой кадр в пространстве может быть описан матрицей вращения, смещение между ними также может быть описано матрицей вращения. Поскольку $A\; 0\; \{\backslash \; displaystyle\; A\_\; \{0\}\}$и $A\; f\; \{\backslash \; displaystyle\; A\_\; \{f\}\}$две матрицы, матрица углового смещения между ними может можно получить как $\Delta \; A\; =\; A\; f.\; A\; 0–1\; \{\backslash \; displaystyle\; \backslash \; Delta\; A\; =\; A\_\; \{f\}.A\_\; \{0\}\; ^\; \{-\; 1\}\}$. Когда это произведение выполняется с очень небольшой разницей между обоими кадрами, мы получим матрицу, близкую к единице.

В пределе у нас будет бесконечно малая матрица вращения.

Бесконечно малое угловое смещение - это матрица бесконечно малого вращения :

• Поскольку любая матрица вращения имеет единственное действительное собственное значение, равное +1, это собственное значение показывает ось вращения.
• Его модуль может быть выведен из значения бесконечно малого вращения.
• Форма матрицы следующая:

$A\; =\; (1\; -\; d\; \varphi \; z\; (t)\; d\; \varphi \; y\; (t)\; d\; \varphi \; z\; (t)\; 1\; -\; d\; \varphi \; x\; (t)\; -\; d\; \varphi \; y\; (t)\; d\; \varphi \; x\; (t)\; 1)\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; -d\; \backslash \; phi\; \_\; \{z\}\; (t)\; d\; \backslash \; phi\; \_\; \{y\}\; (t)\; \backslash \backslash \; d\; \backslash \; phi\; \_\; \{z\}\; (t)\; 1\; -d\; \backslash \; phi\; \_\; \{x\}\; (t)\; \backslash \backslash \; -\; d\; \backslash \; phi\; \_\; \{y\}\; (t)\; d\; \backslash \; phi\; \_\; \{x\}\; (t)\; 1\; \backslash \backslash \backslash \; end\; \{pmatrix\}\}\}$

Здесь мы можем ввести тензор бесконечно малых угловых смещений или генератор вращения связан:

$d\; \Phi \; (t)\; =\; (0\; -\; d\; \varphi \; z\; (t)\; d\; \varphi \; y\; (t)\; d\; \varphi \; z\; (t)\; 0\; -\; d\; \varphi \; x\; (t)\; -\; d\; \varphi \; y\; (T)\; d\; \varphi \; Икс\; (T)\; 0)\; \{\backslash \; Displaystyle\; d\; \backslash \; Phi\; (t)\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; -d\; \backslash \; phi\; \_\; \{z\}\; (t)\; d\; \backslash \; phi\; \_\; \{y\}\; (t)\; \backslash \; \backslash \; d\; \backslash \; phi\; \_\; \{z\}\; (t)\; 0\; -d\; \backslash \; phi\; \_\; \{x\}\; (t)\; \backslash \backslash \; -\; d\; \backslash \; phi\; \_\; \{y\}\; (t)\; d\; \backslash \; phi\; \_\; \{x\}\; (t)\; 0\; \backslash \backslash \backslash \; end\; \{pmatrix\}\}\}$

Такой что соответствующая матрица вращения имеет вид $A\; =\; I\; +\; d\; \Phi \; (t)\; \{\backslash \; displaystyle\; A\; =\; I\; +\; d\; \backslash \; Phi\; (t)\}$. Если его разделить на время, получится вектор угловой скорости.

Генераторы вращений

Предположим, мы задаем ось вращения единичным вектором [x, y, z], и предположим, что у нас бесконечно малый поворот угла Δθ об этом векторе. Расширяя матрицу вращения как бесконечное сложение и используя подход первого порядка, матрица вращения ΔR представлена ​​как:

$\Delta \; R\; =\; [1\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 1]\; +\; [0\; z\; -\; y\; -\; z\; 0\; ху\; -\; х\; 0]\; \Delta \; \theta \; =\; I\; +\; A\; \Delta \; \theta .\; \{\backslash \; displaystyle\; \backslash \; Delta\; R\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; +\; \{\backslash \; begin\; \{bmatrix\}\; 0\; z\; -y\; \backslash \backslash \; -\; z\; 0\; x\; \backslash \backslash \; y\; -x\; 0\; \backslash \; end\; \{bmatrix\}\; \}\; \backslash ,\; \backslash \; Delta\; \backslash \; theta\; =\; \backslash \; mathbf\; \{I\}\; +\; \backslash \; mathbf\; \{A\}\; \backslash ,\; \backslash \; Delta\; \backslash \; theta.\}$

Конечный поворот на угол θ вокруг этой оси можно рассматривать как последовательность небольших вращений вокруг та же ось. Аппроксимируя Δθ как θ / N, где N - большое число, поворот θ вокруг оси можно представить как:

$R\; =\; (1\; +\; A\; \theta \; N)\; N\; \approx \; e\; A\; \theta .\; \{\backslash \; Displaystyle\; R\; =\; \backslash \; left\; (\backslash \; mathbf\; \{1\}\; +\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{A\}\; \backslash \; theta\}\; \{N\}\}\; \backslash \; right)\; ^\; \{N\}\; \backslash \; приблизительно\; e\; ^\; \{\backslash \; mathbf\; \{A\}\; \backslash \; theta\}.\}$

Можно видеть, что теорема Эйлера по существу утверждает, что все повороты могут быть представлены в этой форме. Произведение $A\; \theta \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; \backslash \; theta\}$является «генератором» конкретного поворота, будучи вектором (x, y, z), связанным с матрицей A. Это показывает, что матрица вращения и формат оси угол связаны экспоненциальной функцией.

Можно вывести простое выражение для генератора G. Начнем с произвольной плоскости, определяемой парой перпендикулярных единичных векторов a и b. В этой плоскости можно выбрать произвольный вектор x с перпендикуляром y. Затем вычисляется y в терминах x, и подстановка в выражение для вращения в плоскости дает матрицу вращения R, которая включает генератор G = ba - ab.

$x = a cos ⁡ (α) + b sin ⁡ (α) y = - a sin ⁡ (α) + b cos ⁡ (α) cos ⁡ (α) = a T x sin ⁡ (α) = b T xy = - ab T x + ba T x = (ba T - ab T) xx ′ = x cos ⁡ (β) + y sin ⁡ (β) = [I cos ⁡ (β) + (ba T - ab T)) sin ⁡ (β)] x R = I cos ⁡ (β) + (ba T - ab T) sin ⁡ (β) = I cos ⁡ (β) + G sin ⁡ (β) G = ba T - ab T {\ Displaystyle {\ begin {выровнен} х = а \ соз \ влево (\ альфа \ вправо) + б \ грех \ влево (\ альфа \ вправо) \\ у = - а \ грех \ влево (\ альфа \ вправо) + b \ cos \ left (\ alpha \ right) \\\ cos \ left (\ alpha \ right) = a ^ {T} x \\\ sin \ left (\ alpha \ right) = b ^ {T } x \\ y = - ab ^ {T} x + ba ^ {T} x = \ left (ba ^ {T} -ab ^ {T} \ right) x \\\\ x '= x \ cos \ left (\ beta \ right) + y \ sin \ left (\ beta \ right) \\ = \ left [I \ cos \ left (\ beta \ right) + \ left (ba ^ {T} -ab ^ {T} \ right) \ sin \ left (\ beta \ right) \ right] x \\\\ R = I \ cos \ left (\ beta \ right) + \ left (ba ^ {T} -ab ^ { T} \ right) \ sin \ left (\ beta \ right) \\ = I \ cos \ left (\ beta \ right) + G \ sin \ left (\ beta \ right) \\\\ G = ba ^ {T} -ab ^ {T} \\\ end {align}}}$

Чтобы включить векторы вне плоскости во вращение необходимо изменить приведенное выше выражение для R, включив два оператора проекции , которые разделяют пространство. Эту модифицированную матрицу вращения можно переписать как экспоненциальную функцию.

$P\; ab\; =\; -\; G\; 2\; R\; =\; I\; -\; P\; ab\; +\; [I\; cos\; \; (\beta )\; +\; G\; sin\; \; (\beta )]\; P\; ab\; =\; e\; G\; \beta \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; P\_\; \{ab\}\; =\; -\; G\; ^\; \{2\}\; \backslash \backslash \; R\; =\; I-P\_\; \{ab\}\; +\; \backslash \; left\; [I\; \backslash \; cos\; \backslash \; left\; (\backslash \; beta\; \backslash \; right)\; +\; G\; \backslash \; sin\; \backslash \; left\; (\backslash \; beta\; \backslash \; right)\; \backslash \; right]\; P\_\; \{ab\}\; =\; e\; ^\; \{G\; \backslash \; beta\}\; \backslash \backslash \backslash \; конец\; \{выровнено\}\}\}$

С помощью этих генераторов анализ часто бывает проще, чем с полным матрица вращения. Анализ в терминах генераторов известен как алгебра Ли группы вращений.

Связь с алгебрами Ли

Матрицы в алгебре Ли сами по себе не являются вращениями; кососимметричные матрицы - это производные, пропорциональные разности поворотов. Фактическое «дифференциальное вращение» или матрица бесконечно малого вращения имеет вид

$I\; +\; A\; d\; \theta ,\; \{\backslash \; displaystyle\; I\; +\; A\; \backslash ,\; d\; \backslash \; theta\; ~,\}$

где dθ исчезающе мала и A ∈ so (n), например, с A = L x,

$d\; L\; x\; =\; [1\; 0\; 0\; 0\; 1\; -\; d\; \theta \; 0\; d\; \theta \; 1].\; \{\backslash \; displaystyle\; dL\_\; \{x\}\; =\; \backslash \; left\; [\{\backslash \; begin\; \{smallmatrix\}\; 1\; 0\; 0\; \backslash \backslash \; 0\; 1\; -d\; \backslash \; theta\; \backslash \backslash \; 0\; d\; \backslash \; theta\; 1\; \backslash \; end\; \{smallmatrix\}\}\; \backslash \; right].\}$

Правила вычисления следующие обычно, за исключением того, что бесконечно малые второго порядка обычно отбрасываются. С этими правилами эти матрицы не удовлетворяют всем тем же свойствам, что и обычные матрицы конечного вращения при обычном рассмотрении бесконечно малых. Оказывается, порядок, в котором применяются бесконечно малые вращения, не имеет значения. Чтобы увидеть этот пример, обратитесь к бесконечно малым вращениям SO (3).

Экспоненциальное отображение

Соединение алгебры Ли с группой Ли - это экспоненциальное отображение, которое определяется с использованием стандартная матричная экспоненциальная серия для e Для любой кососимметричной матрицы A, exp (A) всегда является матрицей вращения.

Важным практическим примером является 3 × 3 случай. В группе вращений SO (3) показано, что можно идентифицировать каждый A ∈, поэтому (3) с вектором Эйлера ω = θ u, где u = (x, y, z) - вектор единичной величины.

По свойствам идентификации su (2) ≅ ℝ, u находится в нулевом пространстве A. Таким образом, u является остается инвариантным по exp (A) и, следовательно, является осью вращения.

Использование формулы вращения Родригеса в матричной форме с θ = ⁄ 2 + ⁄ 2 вместе со стандартным double формулы углов получаем,

$exp\; \; (A)\; =\; exp\; \; (\theta \; (u\; \cdot \; L))\; =\; exp\; \; ([0\; -\; z\; \theta \; y\; \theta \; z\; \theta \; 0\; -\; x\; \theta \; -\; y\; \theta \; x\; \theta \; 0\; ])\; Знак\; равно\; I\; +\; 2\; соз\; \; \theta \; 2\; грех\; \; \theta \; 2\; u\; \cdot \; L\; +\; 2\; грех\; 2\; \; \theta \; 2\; (и\; \cdot \; L)\; 2,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; exp\; (A)\; \{\}\; =\; \backslash \; exp\; (\backslash \; theta\; (\{\backslash \; boldsymbol\; \{u\; \backslash \; cdot\; L\}\}))\; =\; \backslash \; exp\; \backslash \; left\; (\backslash \; left\; [\{\backslash \; begin\; \{smallmatrix\}\}\; 0\; -z\; \backslash \; theta\; y\; \backslash \; theta\; \backslash \backslash \; z\; \backslash \; theta\; 0\; -x\; \backslash \; theta\; \backslash \backslash \; -\; y\; \backslash \; theta\; x\; \backslash \; theta\; 0\; \backslash \; end\; \{smallmatrix\}\}\; \backslash \; right]\; \backslash \; right)\; =\; \{\backslash \; boldsymbol\; \{I\}\}\; +\; 2\; \backslash \; cos\; \{\backslash \; frac\; \{\backslash \; theta\}\; \{2\}\}\; \backslash \; sin\; \{\backslash \; frac\; \{\backslash \; theta\}\; \{2\}\}\; ~\; \{\backslash \; boldsymbol\; \{u\; \backslash \; cdot\; L\}\}\; +\; 2\; \backslash \; sin\; ^\; \{2\}\; \{\backslash \; frac\; \{\backslash \; theta\}\; \{2\}\}\; ~\; (\{\backslash \; boldsymbol\; \{u\; \backslash \; cdot\; L\}\})\; ^\; \{2\},\; \backslash \; end\; \{align\}\}\}$

где c = cos ⁄ 2, s = sin ⁄ 2.

Это матрица для поворота вокруг оси u на угол θ в полуугловой форме. Для получения полной информации см. экспоненциальная карта SO (3).

Обратите внимание, что для бесконечно малых углов члены второго порядка могут быть проигнорированы и остаются exp (A) = I + A

• Angular расстояние
• Угловая скорость
• Бесконечно малое вращение
• Линейная упругость
• Второй момент площади

1. ^Kleppner, Daniel; Коленков, Роберт (1973). Введение в механику. Макгроу-Хилл. стр. 288 –89.
2. ^в евклидовом пространстве
3. ^(Goldstein, Poole Safko 2002, §4.8) harv error: no target: CITEREFGoldsteinPooleSafko2002 (help )
4. ^(Wedderburn 1934, §8.02) ошибка harv: нет цели: CITEREFWedderburn1934 (help )