Томографическая реконструкция

редактировать

Оценить свойства объекта по конечному числу проекций

Томографическая реконструкция - это тип многомерной обратной задачи, где задача состоит в том, чтобы получить оценку конкретной системы из конечного числа прогнозов. Математическая основа для создания томографических изображений была заложена Иоганном Радоном. Ярким примером применения является реконструкция из компьютерной томографии (КТ), где изображения поперечных сечений пациентов получают неинвазивным способом. В недавних разработках использовалось преобразование Радона и его обратное для задач, связанных с реалистичной вставкой объектов, необходимых для тестирования и оценки использования компьютерной томографии в безопасности аэропорта.

Эта статья относится в целом к методам реконструкции для всех видов томографии, но некоторые термины и физические описания относятся непосредственно к реконструкции рентгеновской компьютерной томографии.

Содержание

1 Введение формулы
2 Алгоритмы реконструкции
- 2.1 Алгоритм реконструкции Фурье-области
- 2.2 Алгоритм обратной проекции
- 2.3 Алгоритм итеративной реконструкции
- 2.4 Реконструкция веерного луча
- 2.5 Реконструкция с глубоким обучением
3 Программное обеспечение для томографической реконструкции
4 Галерея
5 См. Также
6 Ссылки
7 Дополнительная литература
8 Внешние ссылки

Введение в формулу

Рисунок 1: Геометрия параллельного пучка, используемая в томографии и томографической реконструкции. Каждая проекция, полученная в результате томографии под определенным углом, состоит из набора линейных интегралов через объект.

Результирующее томографическое изображение с пластмассового фантома черепа. Проецируемые рентгеновские лучи четко видны на этом срезе, полученном с помощью компьютерной томографии, в виде артефактов изображения из-за ограниченного количества проекционных срезов по углам.

Проекция объекта, полученная в результате томографического измерения процесс под заданным углом $θ {\ displaystyle \ theta}$ $\ theta$ , состоит из набора линейных интегралов (см. рис. 1). Набор из множества таких проекций под разными углами, организованных в 2D, называется синограммой (см. Рис. 3). В рентгеновской компьютерной томографии интеграл линии представляет собой полное ослабление луча рентгеновских лучей, когда он проходит по прямой линии через объект. Как упоминалось выше, результирующее изображение представляет собой 2D (или 3D) модель коэффициента затухания. То есть мы хотим найти изображение $μ (x, y) {\ displaystyle \ mu (x, y)}$ $\ mu (x, y)$ . Самый простой и легкий способ визуализировать метод сканирования - это система параллельной проекции, которая использовалась в первых сканерах. Для этого обсуждения мы рассматриваем данные, которые должны быть собраны как серию параллельных лучей в позиции $r {\ displaystyle r}$ $r$ , через проекцию под углом $θ {\ displaystyle \ theta}$ $\ theta$ . Это повторяется для разных углов. Затухание происходит экспоненциально в ткани:

I = I 0 exp ⁡ (- ∫ μ (x, y) ds) {\ displaystyle I = I_ {0} \ exp \ left ({- \ int \ mu (x, y) \, ds} \ right)}

I = I_ {0} \ exp \ left ({- \ int \ mu (x, y) \, ds} \ right)

где $μ (x, y) {\ displaystyle \ mu (x, y)}$ $\ mu (x, y)$ - коэффициент ослабления как функция положения. Следовательно, обычно общее затухание $p {\ displaystyle p}$ $p$ луча в позиции $r {\ displaystyle r}$ $r$ на проекции под углом $θ {\ displaystyle \ theta}$ $\ theta$ , дается линейным интегралом:

p θ (r) = ln ⁡ (II 0) = - ∫ μ (x, y) ds {\ displaystyle p_ {\ theta} (r) = \ ln \ left ({\ frac {I} {I_ {0}}} \ right) = - \ int \ mu (x, y) \, ds}

{\ displaystyle p _ {\ theta} (r) = \ ln \ left ({\ frac {I} {I_ {0}}} \ right) = - \ int \ mu (x, y) \, ds}

Использование координаты в системе на Рисунке 1 значение $r {\ displaystyle r}$ $r$ , на которое точка $(x, y) {\ displaystyle (x, y)}$ $(x, y)$ будет проецироваться под углом $θ {\ displaystyle \ theta}$ $\ theta$ определяется как:

x cos ⁡ θ + y sin ⁡ θ = r {\ displaystyle x \ cos \ theta + y \ sin \ theta = r \}

x \ cos \ theta + y \ sin \ theta = r \

Таким образом, приведенное выше уравнение можно переписать как

p θ (r) = ∫ - ∞ ∞ ∫ - ∞ ∞ f (x, y) δ (x cos ⁡ θ + y sin ⁡ θ - r) dxdy {\ displaystyle p _ {\ theta} (r) = \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x, y) \ delta (x \ cos \ theta + y \ sin \ theta -r) \, dx \, dy}

{\ displaystyle p _ {\ theta} (r) = \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x, y) \ delta (x \ cos \ theta + y \ sin \ theta -r) \, dx \, dy}

где $f (x, y) {\ displaystyl ef (x, y)}$ $f (Икс, Y)$ представляет $μ (x, y) {\ displaystyle \ mu (x, y)}$ $\ mu (x, y)$ и $δ () {\ displaystyle \ delta ()}$ $\ delta ()$ - это дельта-функция Дирака. Эта функция известна как преобразование Радона (или синограмма) 2D-объекта.

Преобразование Фурье проекции можно записать как

$P θ (ω) = ∫ - ∞ ∞ ∫ - ∞ ∞ f (x, y) exp ⁡ [- j ω (Икс соз ⁡ θ + Y грех ⁡ θ)] dxdy = F (Ω 1, Ω 2) {\ Displaystyle P _ {\ theta} (\ omega) = \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x, y) \ exp [-j \ omega (x \ cos \ theta + y \ sin \ theta)] \, dx \, dy = F (\ Omega _ {1}, \ Omega _ {2})}$ ${\ displaystyle P _ {\ theta} (\ omega) = \ int _ {- \ infty } ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x, y) \ exp [-j \ omega (x \ cos \ theta + y \ sin \ theta)] \, dx \, dy = F (\ Omega _ {1}, \ Omega _ {2})}$ где $Ω 1 = ω cos ⁡ θ, Ω 2 = ω sin ⁡ θ {\ displaystyle \ Omega _ {1} = \ omega \ cos \ theta, \ Omega _ {2} = \ omega \ sin \ theta}$ ${\ displaystyle \ Omega _ {1} = \ omega \ cos \ theta, \ Omega _ {2} = \ omega \ sin \ theta}$

$P θ (ω) {\ displaystyle P _ {\ theta} (\ omega)}$ ${\ displaystyle P_ {\ theta} (\ omega)}$ представляет собой часть двумерное преобразование Фурье $f (x, y) {\ displaystyle f (x, y)}$ $f (Икс, Y)$ под углом $θ {\ displaystyle \ theta}$ $\ theta$ . Используя обратное преобразование Фурье , можно легко получить формулу обратного преобразования Радона.

$е (x, y) знак равно 1 2 π ∫ 0 π g θ (x соз ⁡ θ + y sin ⁡ θ) d θ {\ displaystyle f (x, y) = {\ frac {1} {2 \ pi}} \ int \ limits _ {0} ^ {\ pi} g _ {\ theta} (x \ cos \ theta + y \ sin \ theta) d \ theta}$ ${\ displaystyle f (x, y) = {\ frac {1} {2 \ pi}} \ int \ limits _ {0} ^ {\ pi} g _ {\ theta} (x \ соз \ тета + y \ грех \ тета) d \ тета}$

где $g θ (x cos ⁡ θ + y грех ⁡ θ) {\ displaystyle g _ {\ theta} (x \ cos \ theta + y \ sin \ theta)}$ ${\ displaystyle g _ {\ theta} (x \ cos \ theta + y \ sin \ theta)}$ - производная от преобразования Гильберта от $p θ (r) {\ displaystyle p _ {\ theta} (r)}$ ${\ displaystyle p _ {\ theta} (r)}$

Теоретически обратное преобразование Радона даст исходное изображение. Теорема проекции-среза говорит нам, что если бы у нас было бесконечное количество одномерных проекций объекта, сделанных под бесконечным числом углов, мы могли бы идеально восстановить исходный объект, $f (x, y) {\ displaystyle f (x, y)}$ $f (Икс, Y)$ . Однако на практике будет доступно лишь ограниченное число прогнозов.

Предположим, что $f (x, y) {\ displaystyle f (x, y)}$ $f (Икс, Y)$ имеет эффективный диаметр $d {\ displaystyle d}$ $d$ и желаемое разрешение: $R s {\ displaystyle R_ {s}}$ $R_s$ , простое правило, количество проекций, необходимых для реконструкции: $N>π d / R s {\ displaystyle N>\ pi d / R_ {s}}$ $N>\ pi d / R_ {s}$

Алгоритмы реконструкции

Практические алгоритмы реконструкции были разработаны для реализации процесса реконструкции 3- Эти алгоритмы разработаны в основном на основе математики преобразования Радона, статистических знаний о процессе сбора данных и геометрии системы визуализации данных.

Алгоритм реконструкции области Фурье

Реконструкция может быть выполнена с использованием интерполяции. Предположим, $N {\ displaysty le N}$ $N$ -проекции $f (x, y) {\ displaystyle f (x, y)}$ $f (Икс, Y)$ генерируются под одинаковыми углами, каждая из которых измеряется с одинаковой частотой. Дискретное преобразование Фурье на каждой проекции даст выборку в частотной области. Объединение всех проекций с частотной дискретизацией приведет к созданию полярного растра в частотной области. Полярный растр будет разреженным, поэтому для заполнения неизвестных точек ДПФ используется интерполяция, а реконструкция может быть выполнена с помощью обратного дискретного преобразования Фурье. Производительность реконструкции можно улучшить, разработав методы для изменения разреженности полярного растра, что повысит эффективность интерполяции.

Например, концентрический квадратный растр в частотной области может быть получен путем изменения угла между каждой проекцией следующим образом:

$θ ′ = R 0 max {| cos ⁡ θ |, | грех ⁡ θ | } {\ displaystyle \ theta '= {\ frac {R_ {0}} {\ max \ {| \ cos \ theta |, | \ sin \ theta | \}}}}$ $\theta '={\frac {R_{0}}{\max\{|\cos \theta |,|\sin \theta |\}}}$

где $R 0 { \ displaystyle R_ {0}}$ $R_ {0}$ - самая высокая частота для оценки.

Концентрический квадратный растр повышает эффективность вычислений, позволяя размещать все позиции интерполяции на прямоугольной решетке ДПФ. Кроме того, это уменьшает ошибку интерполяции. Тем не менее, у алгоритма преобразования Фурье есть недостаток, заключающийся в том, что на выходе получается шумный по своей сути.

Алгоритм обратной проекции

На практике восстановления томографических изображений часто используется стабилизированная и дискретизированная версия обратного преобразования Радона, известная как с обратной фильтрацией. алгоритм проекции.

Для дискретной системы с дискретизацией обратное преобразование Радона равно

$f (x, y) = 1 2 π ∑ i = 0 N - 1 Δ θ ig θ i (x соз ⁡ θ я + Y грех ⁡ θ я) {\ displaystyle f (x, y) = {\ frac {1} {2 \ pi}} \ sum _ {i = 0} ^ {N-1} \ Delta \ theta _ {i} g _ {\ theta _ {i}} (x \ cos \ theta _ {i} + y \ sin \ theta _ {i})}$ ${\ displaystyle f (x, y) = {\ frac {1} {2 \ pi}} \ sum _ {i = 0} ^ {N-1 } \ Delta \ theta _ {i} g _ {\ theta _ {i}} (x \ cos \ theta _ {i} + y \ sin \ theta _ {i})}$

$g θ (t) = p θ (t) ⋅ К (T) {\ Displaystyle g _ {\ theta} (t) = p _ {\ theta} (t) \ cdot k (t)}$ ${\ displaystyle g _ {\ theta} (t) = p _ {\ theta} (t) \ cdot k (t)}$

где $Δ θ {\ displaystyle \ Delta \ theta}$ $\ Delta \ theta$ - угловое расстояние между выступами, а $k (t) {\ displaystyle k (t)}$ ${\ displaystyle k (t)}$ - ядро радона с частотной характеристикой $| ω | {\ displaystyle | \ omega |}$ ${\ displaystyle | \ omega |}$ .

Название "обратная проекция" происходит от того факта, что одномерная проекция должна быть отфильтрована одномерным ядром Радона (обратная проекция), чтобы получить двухмерный сигнал. Используемый фильтр не содержит усиления постоянного тока, поэтому добавление смещения постоянного тока может быть желательным. Реконструкция с использованием обратной проекции обеспечивает лучшее разрешение, чем метод интерполяции, описанный выше. Однако он вызывает больший шум, потому что фильтр склонен усиливать высокочастотный контент.

Алгоритм итеративного восстановления

Итерационный алгоритм требует больших вычислительных ресурсов, но позволяет включать априорную информацию о системе $f (x, y) {\ displaystyle f (x, y)}$ $f (Икс, Y)$ .

Пусть $N {\ displaystyle N}$ $N$ будет количеством проекций, $D i {\ displaystyle D_ {i}}$ $D_ {i}$ будет оператором искажения для $i {\ displaystyle i}$ $i$ th проекция, сделанная под углом $θ i {\ displaystyle \ theta _ {i}}$ $\ theta _ {i}$ . ${λ i} {\ displaystyle \ {\ lambda _ {i} \}}$ $\ {\ lambda _ {i} \}$ - это набор параметров для оптимизации преобразования итераций.

$е 0 (Икс, Y) знак равно ∑ я знак равно 1 N λ ip θ я (г) {\ Displaystyle F_ {0} (х, у) = \ сумма _ {я = 1} ^ {N} \ лямбда _ {i} p _ {\ theta _ {i}} (r)}$ ${\ displaystyle f_ {0} (x, y) = \ sum _ {i = 1} ^ {N} \ lambda _ {i} p _ {\ theta _ {i}} (r)}$

Веерная реконструкция фантома Шеппа-Логана с другим расстоянием между датчиками. Меньшее расстояние между датчиками позволяет более точно реконструировать. Рисунок был создан с использованием MATLAB.

$fk (x, y) = fk - 1 (x, y) + ∑ i = 1 N λ i [p θ i (r) - D ifk - 1 (x, y))] {\ displaystyle f_ {k} (x, y) = f_ {k-1} (x, y) + \ sum _ {i = 1} ^ {N} \ lambda _ {i} [p _ {\ theta _ {i}} (r) -D_ {i} f_ {k-1} (x, y)]}$ ${\ displaystyle f_ {k} (x, y) = f_ {k-1} (x, y) + \ sum _ {i = 1} ^ {N} \ lambda _ {i} [p _ {\ theta _ {i}} (r) -D_ {i} f_ {k-1} (x, y)]}$

Альтернативным семейством рекурсивных алгоритмов томографической реконструкции являются методы алгебраической реконструкции и итеративная разреженная асимптотическая минимальная дисперсия.

Реконструкция веерного пучка

Использование неколлимированного веерного пучка является обычным, поскольку получить коллимированный пучок излучения трудно. Веерные лучи будут генерировать серию линейных интегралов, не параллельных друг другу, в качестве проекций. Система веерного луча потребует диапазона углов в 360 градусов, что налагает механические ограничения, однако она позволяет быстрее получать сигнал, что может быть выгодным в определенных условиях, например, в области медицины. Обратное проецирование следует аналогичной двухэтапной процедуре, которая приводит к реконструкции путем вычисления обратных проекций взвешенной суммы, полученных из фильтрованных проекций.

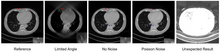Реконструкция с глубоким обучением

Влияние пуассоновского шума при реконструкции с глубоким обучением, когда пуассоновский шум приводит к тому, что U-Net не может восстановить существующий высококонтрастный объект, похожий на поражение.

Методы глубокого обучения широко применяются для реконструкции изображений в настоящее время и достигли впечатляющих результатов в различных задачах реконструкции изображений, включая шумоподавление с малой дозой, реконструкцию разреженного изображения, томографию с ограниченным углом и уменьшение металлических артефактов. Прекрасный обзор можно найти в специальном выпуске IEEE Transaction on Medical Imaging. Одна группа алгоритмов реконструкции с глубоким обучением применяет нейронные сети постобработки для достижения реконструкции изображения в изображение, когда входные изображения восстанавливаются обычными методами реконструкции. Примером такого применения является уменьшение артефактов с помощью U-Net в томографии с ограниченным углом. Однако неправильные структуры могут возникать в изображении, восстановленном таким полностью управляемым данными методом, как показано на рисунке. Следовательно, интеграция известных операторов в архитектуру нейронных сетей оказывается полезной, как описано в концепции точного обучения. Например, прямая реконструкция изображения из данных проекции может быть изучена в рамках фильтрованной обратной проекции. Другой пример - построение нейронных сетей путем развертывания алгоритмов итеративной реконструкции. За исключением прецизионного обучения, использование обычных методов реконструкции с предварительной реконструкцией с глубоким обучением также является альтернативным подходом для улучшения качества изображения при реконструкции с глубоким обучением.

Программное обеспечение для томографической реконструкции

Для гибкой томографической реконструкции доступны наборы инструментов с открытым исходным кодом, такие как PYRO-NN, TomoPy, CONRAD, ODL, ASTRA toolbox и TIGRE. TomoPy - это набор инструментов Python с открытым исходным кодом для выполнения задач обработки томографических данных и реконструкции изображений в Advanced Photon Source в Аргоннской национальной лаборатории. Набор инструментов TomoPy специально разработан для простоты использования и развертывания на линии синхротронного оборудования. Он поддерживает чтение многих распространенных форматов данных синхротрона с диска посредством обмена научными данными и включает несколько других алгоритмов обработки, обычно используемых для данных синхротрона. TomoPy также включает несколько алгоритмов реконструкции, которые можно запускать на многоядерных рабочих станциях и крупномасштабных вычислительных средствах. ASTRA Toolbox - это набор инструментов MATLAB и Python, состоящий из высокопроизводительных примитивов графического процессора для 2D и 3D томографии, с 2009 по 2014 год, разработанный iMinds-Vision Lab, Университет Антверпена и с 2014 года совместно разработанный iMinds-VisionLab (теперь imec-VisionLab), UAntwerpen и CWI, Амстердам. Набор инструментов поддерживает параллельный, веерный и конусный луч с очень гибким расположением источника / детектора. Большое количество алгоритмов реконструкции доступно через TomoPy и набор инструментов ASTRA, включая FBP, Gridrec, ART, SIRT, SART, BART, CGLS, PML, MLEM и OSEM. Недавно набор инструментов ASTRA был интегрирован в структуру TomoPy. Благодаря интеграции набора инструментов ASTRA в структуру TomoPy, оптимизированные методы реконструкции на основе графического процессора становятся легко доступными для пользователей синхротронного луча, а пользователи набора инструментов ASTRA могут более легко читать данные и использовать другие функции TomoPy для фильтрации данных и исправления артефактов.

Галерея

В галерее показан полный процесс для простой томографии объекта и последующей томографической реконструкции на основе ART.

Рис. 2: Призрачный объект, два квадрата с углами.
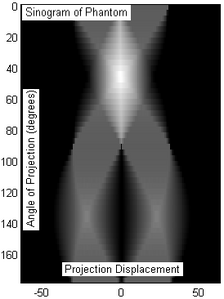
Рис. 3: Синограмма фантомного объекта (Рис. 2), полученная в результате томографии. 50 проекционных срезов были сняты под углом 180 градусов, эквидистантно отобранных (только по совпадению смещение по оси x составляет -50/50 единиц).
Фиг.4: ART томографическая реконструкция синограммы на фиг.3, представленная в виде анимации в процессе итеративной реконструкции. Исходный объект можно приблизительно реконструировать, так как полученное изображение имеет некоторые визуальные артефакты.

См. Также

Ссылки

Дополнительная литература

Авинаш Как и Малкольм Слэйни (1988), Принципы компьютерной томографической визуализации, IEEE Press, ISBN 0-87942-198-3.
Bruyant, PP «Аналитические и итерационные алгоритмы реконструкции в ОФЭКТ» Journal of Nuclear Medicine 43 (10): 1343-1358, 2002

Внешние ссылки

Слэни, А.С.Как и Малкольм. «Принципы компьютерной томографии». Slaney.org. Проверено 7 сентября 2018 г.
Insight ToolKit; программное обеспечение для томографической поддержки с открытым исходным кодом
"TomoPy - документация TomoPy 1.1.3". Tomopy.readthedocs.org. Проверено 7 сентября 2018 г.
Набор инструментов ASTRA (All Scales Tomographic Reconstruction Antwerp); очень гибкое, быстрое программное обеспечение с открытым исходным кодом для компьютерной томографической реконструкции
NiftyRec; комплексное программное обеспечение для томографической реконструкции с открытым исходным кодом; Matlab и Python с поддержкой сценариев
Инструмент томографической реконструкции и визуализации с открытым исходным кодом
«ITS plc - Томография электрических процессов для промышленной визуализации». Itoms.com. Проверено 7 сентября 2018 г.