Скрытое размещение Дирихле

В обработке естественного языка скрытое распределение Дирихле (LDA ) - это генеративная статистическая модель, которая позволяет объяснять наборы наблюдений ненаблюдаемыми группами, которые объясняют, почему некоторые части данных похожи. Например, если наблюдения представляют собой слова, собранные в документы, он предполагает, что каждый документ представляет собой смесь небольшого количества тем и что присутствие каждого слова связано с одной из тем документа. LDA является примером тематической модели и относится к набору инструментов машинного обучения и, в более широком смысле, к набору инструментов искусственного интеллекта.

• 1 История
• 2 Обзор
  • 2.1 Эволюционная биология и биомедицина
  • 2.2 Инженерия
• 3 Модель
  • 3.1 Генеративный процесс
  • 3.2 Определение
• 4 Заключение
  • 4.1 Моделирование Монте-Карло
  • 4.2 Вариационный Байес
  • 4.3 Максимизация правдоподобия
  • 4.4 Неизвестное количество популяций / тем
  • 4.5 Альтернативные подходы
  • 4.6 Аспекты вычислительных деталей
• 5 Связанные проблемы
  • 5.1 Связанные модели
  • 5.2 Пространственные модели
• 6 См. Также
• 7 Ссылки
• 8 Внешние ссылки

В контексте популяционной генетики, LDA был предложен Дж. К. Причард, М. Стивенс и П. Доннелли в 2000 году.

LDA применялось в машинном обучении Дэвидом Блей, Эндрю Нг и Майклом И. Джордан в 2003 году.

Эволюционная биология и биомедицина

В эволюционной биологии и биомедицине модель используется для обнаружения присутствия структурированных генетическая изменчивость в группе лиц. Модель предполагает, что аллели, принадлежащие исследуемым людям, происходят из различных существующих или прошлых популяций. Модель и различные алгоритмы вывода позволяют ученым оценивать частоты аллелей в этих исходных популяциях и происхождение аллелей, переносимых исследуемыми людьми. Исходные популяции можно интерпретировать постфактум с точки зрения различных эволюционных сценариев. В ассоциативных исследованиях обнаружение наличия генетической структуры считается необходимым предварительным шагом, чтобы избежать смешения.

инженерии

Одним из примеров LDA в инженерии является автоматическая классификация документов и оцените их актуальность для различных тем.

В LDA каждый документ можно рассматривать как смесь различных разделов, где каждый документ считается имеющим набор разделов, назначенных ему через LDA. Это идентично вероятностному латентно-семантическому анализу (pLSA), за исключением того, что в LDA предполагается, что распределение тем имеет разреженный Dirichlet предшествующий. Редкие априорные значения Дирихле кодируют интуицию, что документы охватывают лишь небольшой набор тем и что в темах часто используется только небольшой набор слов. На практике это приводит к лучшему устранению неоднозначности слов и более точному распределению документов по темам. LDA - это обобщение модели pLSA, которая эквивалентна LDA при равномерном априорном распределении Дирихле.

Например, модель LDA может иметь разделы, которые можно классифицировать как CAT_related и DOG_related . Тема может генерировать различные слова, такие как молоко, мяуканье и котенок, которые могут быть классифицированы и интерпретированы зрителем как "CAT_related". Естественно, что само слово «кошка» будет иметь большую вероятность в данной теме. Тема, связанная с DOG_related, также имеет вероятность генерирования каждого слова: щенок, лай и кость могут иметь высокую вероятность. Слова без особой значимости, такие как «the» (см. функциональное слово ), будут иметь примерно одинаковую вероятность между классами (или могут быть помещены в отдельную категорию). Тема не имеет четкого определения ни семантически, ни эпистемологически. Выявляется на основе автоматического определения вероятности совпадения терминов. Лексическое слово может встречаться в нескольких темах с разной вероятностью, однако с разным типичным набором соседних слов в каждой теме.

Предполагается, что каждый документ охарактеризован определенным набором тем. Это похоже на стандартное допущение модели пакета слов и делает отдельные слова взаимозаменяемыми.

Обозначение на пластине, представляющее модель LDA.

С обозначение на табличке, которое часто используется для представления вероятностных графических моделей (PGM), зависимости между многими переменными могут быть кратко зафиксированы. Ящики представляют собой «тарелки», представляющие реплики, которые являются повторяющимися объектами. Внешняя пластина представляет документы, а внутренняя пластина представляет повторяющиеся позиции слов в данном документе; каждая позиция связана с выбором темы и слова. Имена переменных определены следующим образом:

M обозначает количество документов

N - количество слов в данном документе (документ i имеет $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$слов)

α - параметр предшествующего Дирихле в распределении тем по каждому документу

β - параметр предшествующего Дирихле при распределении слов по темам

$\theta \; i\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{i\}\}$- распределение тем для документа i

$;\; \phi \; k\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{k\}\}$- это распределение слов для темы k

$zij\; \{\backslash \; displaystyle\; z\_\; \{ij\}\}$- тема для j-го слова в документе i

$wij\; \{\backslash \; displaystyle\; w\_\; \{ij\}\}$- это конкретное слово.

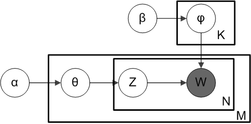
Обозначение на табличке для LDA с распределением тематических слов по Дирихле

Тот факт, что W выделен серым цветом, означает, что слова $wij\; \{\backslash \; displaystyle\; w\_\; \{ij\}\}$- единственные наблюдаемые переменные, а остальные переменные - скрытые переменные. Как было предложено в исходной статье, редкий априор Дирихле можно использовать для моделирования распределения тематических слов, следуя интуиции, что распределение вероятностей по словам в теме искажено, так что только небольшой набор слов имеет высокую вероятность. Полученная модель является наиболее широко применяемым вариантом LDA сегодня. Обозначение на табличке для этой модели показано справа, где $K\; \{\backslash \; displaystyle\; K\}$обозначает количество тем, а $\phi \; 1,\dots ,\; \phi \; K\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; varphi\; \_\; \{K\}\}$- это $V\; \{\backslash \; displaystyle\; V\}$-мерные векторы, хранящие параметры тематического слова, распределенного по Дирихле. распределения ($V\; \{\backslash \; displaystyle\; V\}$- количество слов в словаре).

Полезно рассматривать сущности, представленные $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$и $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$как матрицы, созданные путем декомпозиции исходной матрицы документа-слова, представляющей корпус моделируемых документов. В этом представлении $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$состоит из строк, определенных документами, и столбцов, определенных тем, а $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$состоит из строк, определяемых темами, и столбцов, определяемых словами. Таким образом, $\phi \; 1,\dots ,\; \phi \; K\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; varphi\; \_\; \{K\}\}$относится к набору строк или векторов, каждый из который является распределением по словам, а $\theta \; 1,\dots ,\; \theta \; M\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\},\; \backslash \; dots,\; \backslash \; theta\; \_\; \{M\}\}$относится к набору строк, каждая из которых представляет собой распределение по темам.

Генерирующий процесс

Чтобы фактически вывести темы в корпусе, мы представляем генерирующий процесс, посредством которого создаются документы, так что мы можем сделать вывод или реконструировать их. Мы представляем себе порождающий процесс следующим образом. Документы представлены как случайные смеси по скрытым темам, где каждая тема характеризуется распределением по всем словам. LDA предполагает следующий процесс генерации для корпуса $D\; \{\backslash \; displaystyle\; D\}$, состоящего из $M\; \{\backslash \; displaystyle\; M\}$документов, каждый длиной $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$:

1. Выберите $\theta \; i\; \sim \; Dir\; \; (\alpha )\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{i\}\; \backslash \; sim\; \backslash \; operatorname\; \{Dir\}\; (\backslash \; alpha)\}$, где $i\; \in \; \{1,\dots ,\; M\}\; \{\backslash \; displaystyle\; i\; \backslash \; in\; \backslash \; \{1,\; \backslash \; dots,\; M\; \backslash \}\}$и $D\; ir\; (\alpha )\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Dir\}\; (\backslash \; alpha)\}$- это распределение Дирихле с симметричным параметром $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$, который обычно является разреженным ()

2. Выберите $\phi \; k\; \sim \; Dir\; \; (\beta )\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{k\}\; \backslash \; sim\; \backslash \; operatorname\; \{Dir\}\; (\backslash \; beta)\}$, где $k\; \in \; \{1,\dots ,\; K\}\; \{\backslash \; displaystyle\; k\; \backslash \; in\; \backslash \; \{1,\; \backslash \; dots,\; K\; \backslash \}\}$и $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$обычно разреженные

3. Для каждого позиций слов $i,\; j\; \{\backslash \; displaystyle\; i,\; j\}$, где $i\; \in \; \{1,\dots ,\; M\}\; \{\backslash \; displaystyle\; i\; \backslash \; in\; \backslash \; \{1,\; \backslash \; dots,\; M\; \backslash \}\}$и $j\; \in \; \{1,\dots ,\; N\; i\}\; \{\backslash \; displaystyle\; j\; \backslash \; in\; \backslash \; \{1,\; \backslash \; dots,\; N\_\; \{i\}\; \backslash \}\}$

(a) Выберите тему $zi,\; j\; \sim \; многочлен\; \; (\theta \; i).\; \{\backslash \; Displaystyle\; z\_\; \{i,\; j\}\; \backslash \; sim\; \backslash \; operatorname\; \{Multinomial\}\; (\backslash \; theta\; \_\; \{i\}).\}$

(b) Выберите слово $w\; i,\; j\; \sim \; Multinomial\; \; (\phi \; z\; i,\; j).\; \{\backslash \; displaystyle\; w\_\; \{i,\; j\}\; \backslash \; sim\; \backslash \; operatorname\; \{Multinomial\}\; (\backslash \; varphi\; \_\; \{z\_\; \{i,\; j\}\}).\}$

(Обратите внимание, что полиномиальное распределение здесь относится к полиномиальному только с одним испытанием, которое также известно как категориальное распределение.)

Длина $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$обрабатывается независимо от всех других переменных, генерирующих данные ($w\; \{\backslash \; displaystyle\; w\}$и $z\; \{\backslash \; displaystyle\; z\}$). Нижний индекс часто опускается, как на диаграммах, показанных здесь.

Определение

Формальное описание LDA выглядит следующим образом:

Определение переменных в модели

Переменная	Тип	Значение
$K\; \{\backslash \; displaystyle\; K\}$	integer	количество тем (например, 50)
$V\; \{\backslash \; displaystyle\; V\}$	integer	количество слов в словаре (например, 50 000 или 1 000 000)
$M\; \{\backslash \; displaystyle\; M\}$	integer	количество документов
$N\; d\; =\; 1\dots \; M\; \{\backslash \; displaystyle\; N\_\; \{d\; =\; 1\; \backslash \; dots\; M\}\}$	integer	количество слов в документе d
$N\; \{\backslash \; displaystyle\; N\}$	integer	общее количество слов во всех документах; сумма всех значений $N\; d\; \{\backslash \; displaystyle\; N\_\; \{d\}\}$, т.е. $N\; =\; \sum \; d\; =\; 1\; MN\; d\; \{\backslash \; displaystyle\; N\; =\; \backslash \; sum\; \_\; \{d\; =\; 1\}\; ^\; \{M\}\; N\_\; \{d\}\}$
$\alpha \; k\; =\; 1\dots \; K\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{k\; =\; 1\; \backslash \; dots\; K\}\}$	положительное вещественное число	предшествующий вес темы k в документ; обычно одинаково для всех тем; обычно число меньше 1, например 0.1, чтобы предпочесть редкое распределение тем, то есть несколько тем в документе
$\alpha \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; alpha\}\}\}$	K-мерный вектор положительных вещественных чисел	совокупность всех $\alpha \; k\; \{\backslash \; displaystyle\; \backslash \; alpha\; \_\; \{k\}\}$значения, рассматриваемые как один вектор
$\beta \; w\; =\; 1\dots \; V\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{w\; =\; 1\; \backslash \; dots\; V\}\}$	положительное действительное	предшествующий вес слова w в теме; обычно одинаково для всех слов; обычно число намного меньше 1, например 0,001, чтобы строго предпочесть редкое распределение слов, то есть несколько слов на тему
$\beta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; beta\}\}\}$	V-мерный вектор положительных вещественных чисел	совокупность всех $\beta \; w\; \{\backslash \; displaystyle\; \backslash \; beta\; \_\; \{w\}\}$значений, рассматриваемых как один вектор
$\phi \; k\; =\; 1\dots \; K,\; w\; =\; 1\dots \; V\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{k\; =\; 1\; \backslash \; точки\; K,\; w\; =\; 1\; \backslash \; точки\; V\}\}$	вероятность (действительное число от 0 до 1)	вероятность того, что слово w встречается в теме k
$\phi \; k\; =\; 1\dots \; K\; \{\; \backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; \_\; \{k\; =\; 1\; \backslash \; dots\; K\}\}$	V-мерный вектор вероятностей, который должен суммироваться в 1	распределение слов в теме k
$\theta \; d\; =\; 1\dots \; M,\; k\; =\; 1\dots \; K\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{d\; =\; 1\; \backslash \; dots\; M,\; k\; =\; 1\; \backslash \; dots\; K\}\}$	вероятность (действительное число от 0 до 1)	вероятность появления темы k в документе d
$\theta \; d\; =\; 1\dots \; M\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \_\; \{d\; =\; 1\; \backslash \; dots\; M\}\}$	K-мерный вектор вероятностей, что в сумме должно составлять 1	распределение тем в документе d
$zd\; =\; 1\dots \; M,\; w\; =\; 1\dots \; N\; d\; \{\backslash \; displaystyle\; z\_\; \{d\; =\; 1\; \backslash \; dots\; M,\; w\; =\; 1\; \backslash \; dots\; N\_\; \{d\}\}\}$	целое число от 1 до K	идентичность темы слова w в документе d
$Z\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Z\}\}$	N-мерный вектор целых чисел от 1 до K	идентичность темы всех слов во всех документах
$wd\; =\; 1\dots \; M,\; w\; =\; 1\dots \; N\; d\; \{\backslash \; displaystyle\; w\_\; \{d\; =\; 1\; \backslash \; dots\; M,\; w\; =\; 1\; \backslash \; dots\; N\_\; \{d\}\}\}$	целое число от 1 до V	идентичность слова w в документе d
$W\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{W\}\}$	N-мерный вектор целых чисел от 1 до V	идентичность всех слов во всех документах

Мы можем затем математически описать случайные величины следующим образом:

$\phi \; k\; =\; 1\dots \; K\; \sim \; Dirichlet\; V\; \; (\beta )\; \theta \; d\; =\; 1\dots \; M\; \sim \; Dirichlet\; K\; \; (\alpha )\; zd\; =\; 1\dots \; M,\; w\; =\; 1\dots \; N\; d\; \sim \; категориальный\; К\; \; (\theta \; d)\; wd\; =\; 1\dots \; M,\; w\; =\; 1\dots \; N\; d\; \sim \; категориальный\; V\; \; (\phi \; zdw)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; \_\; \{k\; =\; 1\; \backslash \; dots\; K\}\; \backslash \; sim\; \backslash \; operatorname\; \{Dirichlet\}\; \_\; \{V\}\; (\{\backslash \; boldsymbol\; \{\backslash \; beta\}\})\; \backslash \backslash \; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \_\; \{d\; =\; 1\; \backslash \; dots\; M\}\; \backslash \; sim\; \backslash \; operatorname\; \{Dirichlet\}\; \_\; \{K\}\; (\{\backslash \; boldsymbol\; \{\backslash \; alpha\}\})\; \backslash \backslash \; z\_\; \{d\; =\; 1\; \backslash \; dots\; M,\; w\; =\; 1\; \backslash \; dots\; N\_\; \{d\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{Категориальный\; \}\; \_\; \{K\}\; (\{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \_\; \{d\})\; \backslash \backslash \; w\_\; \{d\; =\; 1\; \backslash \; dots\; M,\; w\; =\; 1\; \backslash \; dots\; N\_\; \{d\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{Категориальный\}\; \_\; \{\; V\}\; (\{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; \_\; \{z\_\; \{dw\}\})\; \backslash \; end\; \{align\}\}\}$

Изучение различных распределений (набор тем, связанные с ними вероятности слов, тема каждого слова и конкретная смесь тем каждого документа) является проблемой статистического вывода.

моделирования Монте-Карло

Исходная статья Pritchard et al. использовали аппроксимацию апостериорного распределения методом Монте-Карло. Альтернативные предложения методов вывода включают выборку Гиббса.

Вариационный байесовский

В исходной статье ML использовалось вариационное байесовское приближение апостериорного распределения ;

максимизация правдоподобия

Прямая оптимизация вероятности с помощью алгоритма релаксации блоков оказывается быстрой альтернативой MCMC.

Неизвестное количество популяций / тем

На практике наиболее адекватное количество население или темы заранее не известны. Это можно оценить путем оценки апостериорного распределения с помощью [Обратимый скачок цепи Маркова Монте-Карло]

Альтернативные подходы

Альтернативные подходы включают распространение математического ожидания.

. Недавние исследования были сосредоточены на ускорение вывода скрытого распределения Дирихле для поддержки захвата огромного количества тем в большом количестве документов. Уравнение обновления свернутого пробоотборника Гиббса, упомянутое в предыдущем разделе, имеет естественную разреженность, которой можно воспользоваться. Интуитивно понятно, поскольку каждый документ содержит только подмножество тем $K\; d\; \{\backslash \; displaystyle\; K\_\; \{d\}\}$, а слово также появляется только в подмножестве тем $K\; w\; \{\backslash \; displaystyle\; K\_\; \{w\}\}$, приведенное выше уравнение обновления можно переписать, чтобы воспользоваться преимуществом этой разреженности.

$p\; (Z\; d,\; n\; =\; k)\; \propto \; \alpha \; \beta \; C\; k\; \neg \; n\; +\; V\; \beta \; +\; C\; kd\; \beta \; C\; k\; \neg \; n\; +\; V\; \beta \; +\; C\; kw\; (\alpha \; +\; C\; kd)\; C\; k\; \neg \; n\; +\; V\; \beta \; \{\backslash \; displaystyle\; p\; (Z\_\; \{d,\; n\}\; =\; k)\; \backslash \; propto\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash \; beta\}\; \{C\_\; \{k\}\; ^\; \{\backslash \; neg\; n\}\; +\; V\; \backslash \; beta\}\}\; +\; \{\backslash \; frac\; \{C\_\; \{k\}\; ^\; \{d\}\; \backslash \; beta\}\; \{C\_\; \{k\}\; ^\; \{\backslash \; neg\; n\}\; +\; V\; \backslash \; beta\}\}\; +\; \{\backslash \; frac\; \{C\_\; \{k\}\; ^\; \{w\}\; (\backslash \; alpha\; +\; C\_\; \{k\}\; ^\; \{d\})\}\; \{C\_\; \{k\}\; ^\; \{\backslash \; neg\; n\}\; +\; V\; \backslash \; beta\}\}\}$

В этом В уравнении у нас есть три члена, два из которых являются разреженными, а другой - маленькими. Мы называем эти термины $a,\; b\; \{\backslash \; displaystyle\; a,\; b\}$и $c\; \{\backslash \; displaystyle\; c\}$соответственно. Теперь, если мы нормализуем каждый член путем суммирования по всем темам, мы получим:

$A\; =\; \sum \; k\; =\; 1\; K\; \alpha \; \beta \; C\; k\; \neg \; n\; +\; V\; \beta \; \{\backslash \; displaystyle\; A\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{K\}\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash \; beta\}\; \{C\_\; \{k\}\; ^\; \{\backslash \; neg\; n\}\; +\; V\; \backslash \; beta\}\}\}$

$B\; =\; \sum \; k\; =\; 1\; KC\; kd\; \beta \; C\; k\; \neg \; n\; +\; V\; \beta \; \{\; \backslash \; displaystyle\; B\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{K\}\; \{\backslash \; frac\; \{C\_\; \{k\}\; ^\; \{d\}\; \backslash \; beta\}\; \{C\_\; \{k\}\; ^\; \{\backslash \; neg\; n\}\; +\; V\; \backslash \; beta\}\}\}$

$C\; =\; \sum \; К\; знак\; равно\; 1\; KC\; квт\; (\alpha \; +\; C\; kd)\; C\; k\; \neg \; n\; +\; V\; \beta \; \{\backslash \; displaystyle\; C\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{K\}\; \{\backslash \; frac\; \{C\_\; \{k\}\; ^\; \{\; w\}\; (\backslash \; alpha\; +\; C\_\; \{k\}\; ^\; \{d\})\}\; \{C\_\; \{k\}\; ^\; \{\backslash \; neg\; n\}\; +\; V\; \backslash \; beta\}\}\}$

Здесь мы видим, что $B\; \{\backslash \; displaystyle\; B\}$- это сумма тем, которые появляются в документе $d\; \{\backslash \; displaystyle\; d\}$и $C\; \{\backslash \; displaystyle\; C\}$также является разреженным суммированием тем, которым присвоено слово $w\; \{\backslash \; displaystyle\; w\}$по всему корпусу. $A\; \{\backslash \; displaystyle\; A\}$, с другой стороны, плотный, но из-за малых значений $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$$\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$, значение очень мало по сравнению с двумя другими членами.

Теперь, при отборе темы, если мы выбираем случайную величину равномерно из $s\; \sim \; U\; (s\; |\; \mid \; A\; +\; B\; +\; C)\; \{\backslash \; displaystyle\; s\; \backslash \; sim\; U\; (s\; |\; \backslash \; mid\; A\; +\; B\; +\; C)\}$, мы можем проверить, в какую корзину приземляется наш образец. Поскольку $A\; \{\backslash \; displaystyle\; A\}$невелик, мы вряд ли попадем в эту ведро; однако, если мы все же попадаем в эту корзину, выборка темы занимает $O\; (K)\; \{\backslash \; displaystyle\; O\; (K)\}$времени (так же, как и исходный сэмплер Collapsed Gibbs). Однако, если мы попадаем в две другие группы, нам нужно будет проверить только подмножество тем, если мы будем вести учет разреженных тем. Выбор темы можно выбрать из сегмента $B\; \{\backslash \; displaystyle\; B\}$за $O\; (K\; d)\; \{\backslash \; displaystyle\; O\; (K\_\; \{d\})\}$время, и тема может быть выбрана из сегмента $C\; \{\backslash \; displaystyle\; C\}$в $O\; (K\; w)\; \{\backslash \; displaystyle\; O\; (K\_\; \{w\})\}$время, где $K\; d\; \{\backslash \; displaystyle\; K\_\; \{d\}\}$и $K\; w\; \{\backslash \; displaystyle\; K\_\; \{w\}\}$обозначает количество тем, назначенных текущий документ и текущий тип слова соответственно.

Обратите внимание, что после выборки каждой темы обновление этих сегментов - это все основные $O\; (1)\; \{\backslash \; displaystyle\; O\; (1)\}$арифметические операции.

Аспекты вычислительных деталей

Ниже приводится вывод уравнений для свернутой выборки Гиббса, что означает $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$s и $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$s будут интегрированы. Для простоты в этом выводе предполагается, что все документы имеют одинаковую длину $N\; \{\backslash \; displaystyle\; N\_\; \{\}\}$. Вывод также действителен, если длина документа различается.

Согласно модели, полная вероятность модели равна:

$P\; (W,\; Z,\; \theta ,\; \phi ;\; \alpha ,\; \beta )\; =\; \prod \; i\; =\; 1\; KP\; (\phi \; i;\; \beta )\; \prod \; j\; Знак\; равно\; 1\; МП\; (\theta \; j;\; \alpha )\; \prod \; T\; знак\; равно\; 1\; NP\; (Z\; J,\; t\; \mid \; \theta \; j)\; п\; (W\; j,\; t\; \mid \; \phi \; Z\; j,\; t),\; \{\backslash \; displaystyle\; P\; (\{\backslash \; boldsymbol\; \{W\}\},\; \{\backslash \; boldsymbol\; \{Z\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\};\; \backslash \; alpha,\; \backslash \; beta)\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; P\; (\backslash \; varphi\; \_\; \{i\};\; \backslash \; beta)\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\; P\; (\backslash \; theta\; \_\; \{j\};\; \backslash \; alpha)\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\; \}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; P\; (W\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; varphi\; \_\; \{Z\_\; \{j,\; t\}\}),\}$

где жирным шрифтом переменные обозначают векторную версию переменных. Во-первых, $\phi \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\}$и $\theta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\}$должны быть интегрирован.

$P\; (Z,\; W;\; \alpha ,\; \beta )\; =\; \int \; \theta \; \int \; \phi \; P\; (W,\; Z,\; \theta ,\; \phi ;\; \alpha ,\; \beta )\; d\; \phi \; d\; \theta \; =\; \int \; \phi \; \prod \; i\; =\; 1\; KP\; (\phi \; i;\; \beta )\; \prod \; j\; =\; 1\; M\; \prod \; t\; =\; 1\; NP\; (W\; j,\; t\; \mid \; \phi \; Z\; j,\; t)\; d\; \phi \; \int \; \theta \; \prod \; j\; =\; 1\; MP\; (\theta \; j;\; \alpha )\; \prod \; t\; =\; 1\; NP\; (Z\; j,\; t\; \mid \; \theta \; j)\; d\; \theta .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; P\; (\{\backslash \; boldsymbol\; \{Z\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\; =\; \backslash \; int\; \_\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \backslash \; int\; \_\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; P\; (\{\backslash \; boldsymbol\; \{W\}\},\; \{\backslash \; boldsymbol\; \{Z\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\};\; \backslash \; alpha,\; \backslash \; beta)\; \backslash ,\; d\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; \backslash ,\; d\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \backslash \backslash \; =\; \{\}\; \backslash \; int\; \_\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; P\; (\backslash \; varphi\; \_\; \{i\};\; \backslash \; beta)\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (W\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; varphi\; \_\; \{Z\_\; \{j,\; t\}\})\; \backslash ,\; d\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\; \backslash \; int\; \_\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\; P\; (\backslash \; theta\; \_\; \{j\};\; \backslash \; alpha)\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; \backslash ,\; d\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}.\; \backslash \; end\; \{выравнивается\}\}\; \}$

Все $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$независимы друг от друга и одинаковы для всех $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$с. Таким образом, мы можем обрабатывать каждый $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$и каждый $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$отдельно. Теперь мы сосредоточимся только на части $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$.

$\int \; \theta \; \prod \; j\; =\; 1\; MP\; (\theta \; j;\; \alpha )\; \prod \; t\; =\; 1\; NP\; (Z\; j,\; t\; \mid \; \theta \; j)\; d\; \theta \; =\; \prod \; j\; =\; 1\; M\; \int \; \theta \; j\; P\; (\theta \; j;\; \alpha )\; \prod \; t\; =\; 1\; NP\; (Z\; j,\; t\; \mid \; \theta \; j)\; d\; \theta \; j.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\; P\; (\backslash \; theta\; \_\; \{j\};\; \backslash \; alpha)\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; \backslash ,\; d\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; =\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\; \}\}\; P\; (\backslash \; theta\; \_\; \{j\};\; \backslash \; alpha)\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; \backslash ,\; d\; \backslash \; theta\; \_\; \{\; j\}.\}$

В дальнейшем мы можем сосредоточиться только на одном $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, а именно:

$\int \; \theta \; j\; P\; (\theta \; j;\; \alpha )\; \prod \; t\; =\; 1\; NP\; (Z\; j,\; t\; \mid \; \theta \; j)\; d\; \theta \; j.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\}\}\; P\; (\backslash \; theta\; \_\; \{j\};\; \backslash \; alpha)\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; \backslash ,\; d\; \backslash \; theta\; \_\; \{j\}.\}$

Фактически, это скрытая часть модели для $jth\; \{\backslash \; displaystyle\; j\; ^\; \{th\}\}$документ. Теперь мы заменим вероятности в приведенном выше уравнении истинным выражением распределения, чтобы записать явное уравнение.

$\int \; \theta \; j\; P\; (\theta \; j;\; \alpha )\; \prod \; t\; =\; 1\; NP\; (Z\; j,\; t\; \mid \; \theta \; j)\; d\; \theta \; j\; =\; \int \; \theta \; j\; \Gamma \; (\sum \; i\; =\; 1\; K\; \alpha \; i)\; \prod \; i\; =\; 1\; K\; \Gamma \; (\alpha \; i)\; \prod \; i\; =\; 1\; K\; \theta \; j,\; i\; \alpha \; i\; -\; 1\; \prod \; t\; =\; 1\; NP\; (Z\; j,\; t\; \mid \; \theta \; j)\; d\; \theta \; j.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\}\}\; P\; (\backslash \; theta\; \_\; \{j\};\; \backslash \; alpha)\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; \backslash ,\; d\; \backslash \; theta\; \_\; \{j\}\; =\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\}\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; right)\}\; \{\backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; Gamma\; (\backslash \; alpha\; \_\; \{i\})\}\}\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; theta\; \_\; \{j,\; i\}\; ^\; \{\backslash \; alpha\; \_\; \{i\}\; -1\}\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; \backslash ,\; d\; \backslash \; theta\; \_\; \{j\; \}.\}$

Пусть $nj,\; ri\; \{\backslash \; displaystyle\; n\_\; \{j,\; r\}\; ^\; \{i\}\}$будет количеством токенов слов в $jth\; \{\backslash \; displaystyle\; j\; ^\; \{th\}\}$документ с тем же символом слова ($rth\; \{\backslash \; displaystyle\; r\; ^\; \{th\}\}$слово в словаре), присвоенный $iith\; \{\; \backslash \; displaystyle\; i\; ^\; \{th\}\}$тема. Итак, $n\; j,\; r\; i\; \{\backslash \; displaystyle\; n\_\; \{j,\; r\}\; ^\; \{i\}\}$трехмерно. Если какое-либо из трех измерений не ограничено конкретным значением, мы используем точку в скобках $(\cdot )\; \{\backslash \; displaystyle\; (\backslash \; cdot)\}$для обозначения. Например, $nj,\; (\cdot )\; i\; \{\backslash \; displaystyle\; n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\}$обозначает количество токенов слов в $jth\; \{\backslash \; displaystyle\; j\; ^\; \{th\}\}$документ, назначенный теме $i\; \{\backslash \; displaystyle\; i\; ^\; \{th\}\}$. Таким образом, большая правая часть приведенного выше уравнения может быть переписана как:

$\prod \; t\; =\; 1\; N\; P\; (Z\; j,\; t\; \mid \; \theta \; j)\; =\; \prod \; i\; =\; 1\; K\; \theta \; j,\; i\; n\; j,\; (\cdot )\; i.\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{t\; =\; 1\}\; ^\; \{N\}\; P\; (Z\_\; \{j,\; t\}\; \backslash \; mid\; \backslash \; theta\; \_\; \{j\})\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; theta\; \_\; \{j,\; i\}\; ^\; \{n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\}.\}$

Таким образом, формула интегрирования $\theta \; j\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{j\}\}$может можно заменить на:

$\int \; \theta \; j\; \Gamma \; (\sum \; i\; =\; 1\; K\; \alpha \; i)\; \prod \; i\; =\; 1\; K\; \Gamma \; (\alpha \; i)\; \prod \; i\; =\; 1\; K\; \theta \; j,\; i\; \alpha \; i\; -\; 1\; \prod \; i\; =\; 1\; K\; \theta \; j,\; ing,\; (\cdot )\; id\; \theta \; j\; =\; \int \; \theta \; j\; \Gamma \; (\sum \; i\; =\; 1\; K\; \alpha \; i)\; \prod \; i\; =\; 1\; K\; \Gamma \; (\alpha \; i)\; \prod \; i\; =\; 1\; K\; \theta \; j,\; ing,\; (\cdot )\; i\; +\; \alpha \; i\; -\; 1\; d\; \theta \; j.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\}\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; right)\}\; \{\backslash \; prod\; \_\; \{\; i\; =\; 1\}\; ^\; \{K\}\; \backslash \; Gamma\; (\backslash \; alpha\; \_\; \{i\})\}\}\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; theta\; \_\; \{j,\; i\}\; ^\; \{\backslash \; alpha\; \_\; \{i\}\; -1\; \}\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; theta\; \_\; \{j,\; i\}\; ^\; \{n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\}\; \backslash ,\; d\; \backslash \; theta\; \_\; \{j\}\; =\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\}\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; right)\}\; \{\backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{\; K\}\; \backslash \; Gamma\; (\backslash \; alpha\; \_\; \{i\})\}\}\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; theta\; \_\; \{j,\; i\}\; ^\; \{n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\; +\; \backslash \; alpha\; \_\; \{i\}\; -1\}\; \backslash ,\; d\; \backslash \; theta\; \_\; \{j\}.\}$

Очевидно, уравнение внутри интегрирования имеет тот же вид, что и распределение Дирихле. Согласно распределению Дирихле,

$\int \; \theta \; j\; \Gamma \; (\sum \; i\; =\; 1\; K\; nj,\; (\cdot )\; i\; +\; \alpha \; i)\; \prod \; i\; =\; 1\; K\; \Gamma \; (nj,\; (\cdot )\; i\; +\; \alpha \; i)\; \prod \; i\; Знак\; равно\; 1\; К\; \theta \; J,\; Inj,\; (\cdot )\; я\; +\; \alpha \; я\; -\; 1\; d\; \theta \; J\; =\; 1.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{\backslash \; theta\; \_\; \{j\}\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{\; i\; =\; 1\}\; ^\; \{K\}\; n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\; +\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; right)\}\; \{\backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; Gamma\; (n\_\; \{\; j,\; (\backslash \; cdot)\}\; ^\; \{i\}\; +\; \backslash \; alpha\; \_\; \{i\})\}\}\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; theta\; \_\; \{j,\; i\}\; ^\; \{n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\; +\; \backslash \; alpha\; \_\; \{i\}\; -1\}\; \backslash ,\; d\; \backslash \; theta\; \_\; \{j\}\; =\; 1.\}$

Таким образом,

$∫ θ j P (θ j; α) ∏ t = 1 NP (Z j, t ∣ θ j) d θ j = ∫ θ j Γ (∑ i = 1 K α i) ∏ i = 1 K Γ (α i) ∏ i = 1 K θ j, ing, (⋅) i + α i - 1 d θ j = Γ (∑ i = 1 K α i) ∏ i = 1 K Γ (α i) ∏ i = 1 K Γ (nj, (⋅) i + α i) Γ ( ∑ i = 1 K nj, (⋅) i + α i) ∫ θ j Γ (∑ i = 1 K nj, (⋅) i + α i) ∏ i = 1 K Γ (nj, (⋅) i + α i) ∏ i = 1 K θ j, inj, (⋅) i + α i - 1 d θ j = Γ (∑ i = 1 K α i) ∏ i = 1 K Γ (α i) ∏ i = 1 K Γ (nj, (⋅) i + α i) Γ (∑ i = 1 K nj, (⋅) i + α i). {\ displaystyle {\ begin {align} \ int _ {\ theta _ {j}} P (\ theta _ {j}; \ alpha) \ prod _ {t = 1} ^ {N} P (Z_ {j, t} \ mid \ theta _ {j}) \, d \ theta _ {j} = \ int _ {\ theta _ {j}} {\ frac {\ Gamma \ left (\ sum _ {i = 1} ^ {K} \ alpha _ {i} \ right)} {\ prod _ {i = 1} ^ {K} \ Gamma (\ alpha _ {i})}} \ prod _ {i = 1} ^ {K } \ theta _ {j, i} ^ {n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i} -1} \, d \ theta _ {j} \\ [8pt] = { } {\ frac {\ Gamma \ left (\ sum _ {i = 1} ^ {K} \ alpha _ {i} \ right)} {\ prod _ {i = 1} ^ {K} \ Gamma (\ alpha _ {i})}} {\ frac {\ prod _ {i = 1} ^ {K} \ Gamma (n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i})} { \ Gamma \ left (\ sum _ {i = 1} ^ {K} n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i} \ right)}} \ int _ {\ theta _ { j}} {\ frac {\ Gamma \ left (\ sum _ {i = 1} ^ {K} n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i} \ right)} {\ prod _ {i = 1} ^ {K} \ Gamma (n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i})}} \ prod _ {i = 1} ^ {K} \ theta _ {j, i} ^ {n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i} -1} \, d \ theta _ {j} \\ [8pt] = {} {\ frac {\ Gamma \ left (\ sum _ {i = 1} ^ {K} \ alpha _ {i} \ right)} {\ prod _ {i = 1} ^ {K} \ Gamma (\ alpha _ {i})}} {\ frac {\ prod _ {i = 1} ^ {K} \ Gamma (n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i})} {\ Gamma \ left (\ sum _ {i = 1} ^ {K} n_ {j, (\ cdot)} ^ {i} + \ alpha _ {i} \ right)}}. \ end {align}}}$

Теперь обратим внимание на $\phi \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\}$часть. На самом деле происхождение части $\phi \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; varphi\}\}\}$очень похоже на $\theta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\}$часть. Здесь мы лишь перечисляем этапы вывода:

$∫ φ ∏ i = 1 KP (φ i; β) ∏ j = 1 M ∏ t = 1 NP (W j, t ∣ φ Z j, t) d φ = ∏ i = 1 K ∫ φ i P (φ i; β) ∏ j = 1 M ∏ t = 1 NP (W j, t ∣ φ Z j, t) d φ i = ∏ i = 1 K ∫ φ i Γ (∑ r = 1 V β r) ∏ r = 1 V Γ (β r) ∏ r = 1 V φ i, r β r - 1 ∏ r = 1 V φ i, rn (⋅), rid φ i = I = 1 K ∫ φ i Γ (∑ r = 1 V β r) ∏ r = 1 V Γ (β r) ∏ r = 1 V φ i, rn (⋅), ri + β r - 1 d φ i = ∏ i = 1 K Γ (∑ r = 1 V β r) ∏ r = 1 V Γ (β r) ∏ r = 1 V Γ (n (⋅), ri + β r) Γ (∑ r = 1 V n (⋅), ri + β r). {\ displaystyle {\ begin {align} \ int _ {\ boldsymbol {\ varphi}} \ prod _ {i = 1} ^ {K} P (\ varphi _ {i}; \ beta) \ prod _ {j = 1} ^ {M} \ prod _ {t = 1} ^ {N} P (W_ {j, t} \ mid \ varphi _ {Z_ {j, t}}) \, d {\ boldsymbol {\ varphi }} \\ [8pt] = {} \ prod _ {i = 1} ^ {K} \ int _ {\ varphi _ {i}} P (\ varphi _ {i}; \ beta) \ prod _ { j = 1} ^ {M} \ prod _ {t = 1} ^ {N} P (W_ {j, t} \ mid \ varphi _ {Z_ {j, t}}) \, d \ varphi _ {i } \\ [8pt] = {} \ prod _ {i = 1} ^ {K} \ int _ {\ varphi _ {i}} {\ frac {\ Gamma \ left (\ sum _ {r = 1} ^ {V} \ beta _ {r} \ right)} {\ prod _ {r = 1} ^ {V} \ Gamma (\ beta _ {r})}} \ prod _ {r = 1} ^ {V } \ varphi _ {i, r} ^ {\ beta _ {r} -1} \ prod _ {r = 1} ^ {V} \ varphi _ {i, r} ^ {n _ {(\ cdot), r } ^ {i}} \, d \ varphi _ {i} \\ [8pt] = {} \ prod _ {i = 1} ^ {K} \ int _ {\ varphi _ {i}} {\ frac {\ Gamma \ left (\ sum _ {r = 1} ^ {V} \ beta _ {r} \ right)} {\ prod _ {r = 1} ^ {V} \ Gamma (\ beta _ {r})}} \ prod _ {r = 1} ^ {V} \ varphi _ {i, r} ^ {n _ {(\ cdot), r} ^ {i} + \ beta _ {r} -1} \, d \ varphi _ {i} \\ [8pt] = {} \ prod _ {i = 1} ^ {K} {\ frac {\ Gamma \ left (\ sum _ {r = 1} ^ {V} \ beta _ {r} \ right)} {\ prod _ {r = 1} ^ {V} \ Gamma (\ beta _ {r})}} {\ frac {\ prod _ {r = 1} ^ {V} \ Gamma (n _ {(\ cdot), r} ^ {i} + \ beta _ {r})} {\ Gamma \ left (\ sum _ {r = 1} ^ {V} n _ {(\ cdot), r} ^ {i} + \ beta _ {r} \ right)}}. \ end {align}}}$

Для ясности здесь мы записываем окончательное уравнение как с $\varphi \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; phi\}\}\}$, так и с $\theta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; theta\}\}\; \}$интегрировано:

$P\; (Z,\; W;\; \alpha ,\; \beta )\; =\; \prod \; j\; =\; 1\; M\; \Gamma \; (\sum \; i\; =\; 1\; K\; \alpha \; i)\; \prod \; i\; =\; 1\; K\; \Gamma \; (\alpha \; i)\; \prod \; i\; =\; 1\; K\; \Gamma \; (nj,\; (\cdot )\; i\; +\; \alpha \; i)\; \Gamma \; (\sum \; i\; =\; 1\; K\; nj,\; (\cdot )\; i\; +\; \alpha \; i)\; \times \; \prod \; i\; =\; 1\; K\; \Gamma \; (\sum \; r\; =\; 1\; V\; \beta \; r)\; \prod \; r\; =\; 1\; V\; \Gamma \; (\beta \; r)\; \prod \; r\; =\; 1\; V\; \Gamma \; (n\; (\cdot ),\; ri\; +\; \beta \; r)\; \Gamma \; (\sum \; r\; =\; 1\; V\; n\; (\cdot ),\; ri\; +\; \beta \; r).\; \{\backslash \; Displaystyle\; P\; (\{\backslash \; boldsymbol\; \{Z\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\; =\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{M\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; right)\}\; \{\backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; Gamma\; (\backslash \; alpha\; \_\; \{i\})\}\}\; \{\backslash \; frac\; \{\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \backslash \; Gamma\; (n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\; +\; \backslash \; alpha\; \_\; \{i\})\}\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\; \}\; ^\; \{K\}\; n\_\; \{j,\; (\backslash \; cdot)\}\; ^\; \{i\}\; +\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; right)\}\}\; \backslash \; times\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{K\}\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{r\; =\; 1\}\; ^\; \{V\}\; \backslash \; beta\; \_\; \{r\}\; \backslash \; right)\}\; \{\backslash \; prod\; \_\; \{r\; =\; 1\}\; ^\; \{V\}\; \backslash \; Gamma\; (\backslash \; beta\; \_\; \{r\})\}\}\; \{\backslash \; frac\; \{\backslash \; prod\; \_\; \{r\; =\; 1\}\; ^\; \{V\}\; \backslash \; Gamma\; (n\; \_\; \{(\backslash \; cdot),\; r\}\; ^\; \{i\}\; +\; \backslash \; beta\; \_\; \{r\})\}\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{r\; =\; 1\}\; ^\; \{V\}\; n\; \_\; \{(\backslash \; cdot),\; r\}\; ^\; \{i\}\; +\; \backslash \; beta\; \_\; \{r\}\; \backslash \; right)\}\}.\}$

Здесь цель Гиббса Сэмплинга - аппроксимировать распределение из $P\; (Z\; \mid \; W;\; \alpha ,\; \beta )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; boldsymbol\; \{Z\}\}\; \backslash \; mid\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\}$. Поскольку $P\; (W;\; \alpha ,\; \beta )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\}$неизменно для любого из Z, уравнения выборки Гиббса могут быть производное от $P\; (Z,\; W;\; \alpha ,\; \beta )\; \{\backslash \; displaystyle\; P\; (\{\backslash \; boldsymbol\; \{Z\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\}$непосредственно. Ключевым моментом является получение следующей условной вероятности:

$P\; (Z\; (m,\; n)\; \mid \; Z\; -\; (m,\; n),\; W;\; \alpha ,\; \beta )\; =\; P\; (Z\; (m,\; n),\; Z\; -\; (\; м,\; п),\; W;\; \alpha ,\; \beta )\; P\; (Z\; -\; (м,\; n),\; W;\; \alpha ,\; \beta ),\; \{\backslash \; displaystyle\; P\; (Z\; \_\; \{(m,\; n)\}\; \backslash \; mid\; \{\backslash \; boldsymbol\; \{Z\; \_\; \{-\; (m,\; n)\}\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\; =\; \{\backslash \; frac\; \{P\; (Z\; \_\; \{(m,\; n)\},\; \{\backslash \; boldsymbol\; \{Z\; \_\; \{-\; (m,\; n))\}\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\}\; \{P\; (\{\backslash \; boldsymbol\; \{Z\; \_\; \{-\; (m,\; n)\}\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta)\}\},\}$

где $Z\; (m,\; n)\; \{\backslash \; displaystyle\; Z\; \_\; \{(m,\; n)\}\}$обозначает $Z\; \{\backslash \; displaystyle\; Z\}$скрытая переменная $nth\; \{\backslash \; displaystyle\; n\; ^\; \{th\}\}$word token в $mth\; \{\backslash \; displaystyle\; m\; ^\; \{th\}\}$документ. И далее мы предполагаем, что его словесным символом является слово $v\; t\; h\; \{\backslash \; displaystyle\; v\; ^\; \{th\}\}$в словаре. $Z\; -\; (m,\; n)\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{Z\; \_\; \{-\; (m,\; n)\}\}\}\}$обозначает все $Z\; \{\backslash \; displaystyle\; Z\}$s, но $Z\; (m,\; n)\; \{\backslash \; displaystyle\; Z\; \_\; \{(m,\; n)\}\}$. Обратите внимание, что выборке Гиббса необходимо только выбрать значение для $Z\; (m,\; n)\; \{\backslash \; displaystyle\; Z\; \_\; \{(m,\; n)\}\}$, в соответствии с указанной выше вероятностью, нам не нужен точное значение

$P\; (Z\; m,\; n\; \mid \; Z\; -\; (m,\; n),\; W;\; \alpha ,\; \beta )\; \{\backslash \; displaystyle\; P\; \backslash \; left\; (Z\_\; \{m,\; n\}\; \backslash \; mid\; \{\backslash \; boldsymbol\; \{Z\; \_\; \{-\; (\; m,\; n)\}\}\},\; \{\backslash \; boldsymbol\; \{W\}\};\; \backslash \; alpha,\; \backslash \; beta\; \backslash \; right)\}$

, но отношения между вероятностями, которые $Z\; (m,\; n)\; \{\backslash \; displaystyle\; Z\; \_\; \{(\; m,\; n)\}\}$может принимать значение. So, the above equation can be simplified as:

$P ( Z ( m, n) = v ∣ Z − ( m, n), W ; α, β) ∝ P ( Z ( m, n) = v, Z − ( m, n), W ; α, β) = ( Γ ( ∑ i = 1 K α i) ∏ i = 1 K Γ ( α i)) M ∏ j ≠ m ∏ i = 1 K Γ ( n j, ( ⋅) i + α i) Γ ( ∑ i = 1 K n j, ( ⋅) i + α i) ( Γ ( ∑ r = 1 V β r) ∏ r = 1 V Γ ( β r)) K ∏ i = 1 K ∏ r ≠ v Γ ( n ( ⋅), r i + β r) ∏ i = 1 K Γ ( n m, ( ⋅) i + α i) Γ ( ∑ i = 1 K n m, ( ⋅) i + α i) ∏ i = 1 K Γ ( n ( ⋅), v i + β v) Γ ( ∑ r = 1 V n ( ⋅), r i + β r) ∝ ∏ i = 1 K Γ ( n m, ( ⋅) i + α i) Γ ( ∑ i = 1 K n m, ( ⋅) i + α i) ∏ i = 1 K Γ ( n ( ⋅), v i + β v) Γ ( ∑ r = 1 V n ( ⋅), r i + β r) ∝ ∏ i = 1 K Γ ( n m, ( ⋅) i + α i) ∏ i = 1 K Γ ( n ( ⋅), v i + β v) Γ ( ∑ r = 1 V n ( ⋅), r i + β r). {\displaystyle {\begin{aligned}P(Z_{(m,n)}=v\mid {\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha,\beta)\\[8pt]\propto P(Z_{(m,n)}=v,{\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha,\beta)\\[8pt]=\left({\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}\right)^{M}\prod _{j\neq m}{\frac {\prod _{i=1}^{K}\Gamma \left(n_{j,(\cdot)}^{i}+\alpha _{i}\right)}{\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot)}^{i}+\alpha _{i}\right)}}\left({\frac {\Gamma \left(\sum _{r=1}^{V}\beta _{r}\right)}{\prod _{r=1}^{V}\Gamma (\beta _{r})}}\right)^{K}\prod _{i=1}^{K}\prod _{r\neq v}\Gamma \left(n_{(\cdot),r}^{i}+\beta _{r}\right){\frac {\prod _{i=1}^{K}\Gamma \left(n_{m,(\cdot)}^{i}+\alpha _{i}\right)}{\Gamma \left(\sum _{i=1}^{K}n_{m,(\cdot)}^{i}+\alpha _{i}\right)}}\prod _{i=1}^{K}{\frac {\Gamma \left(n_{(\cdot),v}^{i}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot),r}^{i}+\beta _{r}\right)}}\\[8pt]\propto {\frac {\prod _{i=1}^{K}\Gamma \left(n_{m,(\cdot)}^{i}+\alpha _{i}\right)}{\Gamma \left(\sum _{i=1}^{K}n_{m,(\cdot)}^{i}+\alpha _{i}\right)}}\prod _{i=1}^{K}{\frac {\Gamma \left(n_{(\cdot),v}^{i}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot),r}^{i}+\beta _{r}\right)}}\\[8pt]\propto \prod _{i=1}^{K}\Gamma \left(n_{m,(\cdot)}^{i}+\alpha _{i}\right)\prod _{i=1}^{K}{\frac {\Gamma \left(n_{(\cdot),v}^{i}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot),r}^{i}+\beta _{r}\right)}}.\end{aligned}}}$

Finally, let $n\; j,\; r\; i,\; -\; (\; m,\; n)\; \{\backslash displaystyle\; n\_\{j,r\}^\{i,-(m,n)\}\}$be the same meaning as $n\; j,\; r\; i\; \{\backslash displaystyle\; n\_\{j,r\}^\{i\}\}$but with the $Z\; (\; m,\; n)\; \{\backslash displaystyle\; Z\_\{(m,n)\}\}$excluded. The above equation can be further simplified leveraging the property of gamma function. We first split the summation and then merge it back to obtain a $k\; \{\backslash displaystyle\; k\}$-independent summation, which could be dropped:

$∝ ∏ i ≠ k Γ ( n m, ( ⋅) i, − ( m, n) + α i) ∏ i ≠ k Γ ( n ( ⋅), v i, − ( m, n) + β v) Γ ( ∑ r = 1 V n ( ⋅), r i, − ( m, n) + β r) Γ ( n m, ( ⋅) k, − ( m, n) + α k + 1) Γ ( n ( ⋅), v k, − ( m, n) + β v + 1) Γ ( ∑ r = 1 V n ( ⋅), r k, − ( m, n) + β r + 1) = ∏ i ≠ k Γ ( n m, ( ⋅) i, − ( m, n) + α i) ∏ i ≠ k Γ ( n ( ⋅), v i, − ( m, n) + β v) Γ ( ∑ r = 1 V n ( ⋅), r i, − ( m, n) + β r) Γ ( n m, ( ⋅) k, − ( m, n) + α k) Γ ( n ( ⋅), v k, − ( m, n) + β v) Γ ( ∑ r = 1 V n ( ⋅), r k, − ( m, n) + β r) ( n m, ( ⋅) k, − ( m, n) + α k + 1) n ( ⋅), v k, − ( m, n) + β v + 1 ∑ r = 1 V n ( ⋅), r k, − ( m, n) + β r + 1 = ∏ i Γ ( n m, ( ⋅) i, − ( m, n) + α i) ∏ i Γ ( n ( ⋅), v i, − ( m, n) + β v) Γ ( ∑ r = 1 V n ( ⋅), r i, − ( m, n) + β r) ( n m, ( ⋅) k, − ( m, n) + α k + 1) n ( ⋅), v k, − ( m, n) + β v + 1 ∑ r = 1 V n ( ⋅), r k, − ( m, n) + β r + 1 ∝ ( n m, ( ⋅) k, − ( m, n) + α k + 1) n ( ⋅), v k, − ( m, n) + β v + 1 ∑ r = 1 V n ( ⋅), r k, − ( m, n) + β r + 1 {\displaystyle {\begin{aligned}\propto \prod _{i\neq k}\Gamma \left(n_{m,(\cdot)}^{i,-(m,n)}+\alpha _{i}\right)\prod _{i\neq k}{\frac {\Gamma \left(n_{(\cdot),v}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}}\Gamma \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}+1\right){\frac {\Gamma \left(n_{(\cdot),v}^{k,-(m,n)}+\beta _{v}+1\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot),r}^{k,-(m,n)}+\beta _{r}+1\right)}}\\[8pt]=\prod _{i\neq k}\Gamma \left(n_{m,(\cdot)}^{i,-(m,n)}+\alpha _{i}\right)\prod _{i\neq k}{\frac {\Gamma \left(n_{(\cdot),v}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}}\Gamma \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _ {k}\right){\frac {\Gamma \left(n_{(\cdot),v}^{k,-(m,n)}+\beta _{v}\right)}{\Gamma \ left (\ sum _ {r = 1} ^ {V} n _ {(\ cdot), r} ^ {k, - (m, n)} + \ beta _ {r} \ right)}} \ left ( n_ {m, (\ cdot)} ^ {k, - (m, n)} + \ alpha _ {k} +1 \ right) {\ frac {n _ {(\ cdot), v} ^ {k, - (m, n)} + \ beta _ {v} +1} {\ sum _ {r = 1} ^ {V} n _ {(\ cdot), r} ^ {k, - (m, n)} + \ beta _ {r} +1}} \\ [8pt] = \ prod _ {i} \ Gamma \ left (n_ {m, (\ cdot)} ^ {i, - (m, n)} + \ alpha _ {i} \ right) \ prod _ {i} {\ frac {\ Gamma \ left (n _ {(\ cdot), v} ^ {i, - (m, n)} + \ beta _ {v} \ right)} {\ Gamma \ left (\ sum _ {r = 1} ^ {V} n _ {(\ cdot), r} ^ {i, - (m, n)} + \ beta _ {r} \ right)}} \ left (n_ {m, (\ cdot)} ^ {k, - (m, n)} + \ alpha _ {k} +1 \ right) {\ frac {n _ {(\ cdot), v} ^ {k, - (m, n)} + \ beta _ {v} +1} {\ sum _ {r = 1} ^ {V} n _ {(\ cdot), r} ^ {k, - (m, n)} + \ beta _ {r} +1}} \\ [8pt] \ propto \ left (n_ {m, (\ cdot)} ^ {k, - (m, n)} + \ alpha _ {k} +1 \ right) {\ frac {n _ {(\ cdot), v} ^ {k, - (m, n)} + \ beta _ {v} +1} {\ sum _ {r = 1} ^ {V} n _ {(\ cdot), r} ^ {k, - (m, n)} + \ beta _ {r} +1}} \ end {align}}}$

Обратите внимание, что та же формула выводится в статье о полиномиальном распределении Дирихле в рамках более общего обсуждения интегрирования априорных значений распределения Дирихле из Байесовская сеть.

Связанные модели

Тематическое моделирование - классическое решение проблемы поиска информации с использованием связанных данных и технологии семантической паутины. К связанным моделям и методам относятся, среди прочего, скрытое семантическое индексирование, анализ независимых компонентов, вероятностное скрытое семантическое индексирование, неотрицательная матричная факторизация и Гамма-распределение Пуассона.

Модель LDA очень модульная и поэтому может быть легко расширена. Основная область интересов - моделирование отношений между темами. Это достигается за счет использования другого распределения на симплексе вместо Дирихле. Модель коррелированных тем следует этому подходу, создавая структуру корреляции между темами с использованием логистического нормального распределения вместо Дирихле. Другое расширение - иерархический LDA (hLDA), где темы объединяются в иерархию с помощью вложенного процесса Китайский ресторан, структура которого извлекается из данных. LDA также может быть расширено до корпуса, в котором документ включает два типа информации (например, слова и имена), как в. Непараметрические расширения LDA включают иерархическую модель процесса Дирихле, которая позволяет неограниченному количеству тем и извлекать их из данных.

Как отмечалось ранее, pLSA аналогичен LDA. Модель LDA - это, по сути, байесовская версия модели pLSA. Байесовская формулировка обычно лучше работает с небольшими наборами данных, потому что байесовские методы позволяют избежать переобучения данных. Для очень больших наборов данных результаты двух моделей имеют тенденцию сходиться. Одно отличие состоит в том, что pLSA использует переменную $d\; \{\backslash \; displaystyle\; d\}$для представления документа в обучающем наборе. Итак, в pLSA, когда представлен документ, который модель еще не видела, мы фиксируем $Pr\; (w\; \mid \; z)\; \{\backslash \; displaystyle\; \backslash \; Pr\; (w\; \backslash \; mid\; z)\}$- вероятность слова под темами - должны быть изучены из обучающей выборки и использовать тот же алгоритм EM для вывода $Pr\; (z\; \mid \; d)\; \{\backslash \; displaystyle\; \backslash \; Pr\; (z\; \backslash \; mid\; d)\}$- тема распределение под $d\; \{\backslash \; displaystyle\; d\}$. Блей утверждает, что этот шаг является обманом, поскольку вы, по сути, перестраиваете модель в соответствии с новыми данными.

Пространственные модели

В эволюционной биологии часто естественно предположить, что географическое положение наблюдаемых особей несут некоторую информацию об их предках. Это рациональный вариант различных моделей генетических данных с географической привязкой.

Варианты LDA использовались для автоматического разделения естественных изображений на категории, такие как «спальня» или «лес», путем обработки изображения как документа., и небольшие участки изображения в виде слов; одна из вариаций называется.

• Вариационные байесовские методы
• Распределение Пачинко
• tf-idf
• Infer.NET

• jLDADMM Пакет Java для моделирования тем на обычных или коротких текстах. jLDADMM включает в себя реализации тематической модели LDA и полиномиальной смеси Дирихле, состоящей из одной темы для каждого документа. jLDADMM также предоставляет реализацию для оценки кластеризации документов для сравнения тематических моделей.
• Пакет Java для моделирования коротких текстовых тем (https://github.com/qiang2100/STTM ). STTM включает следующие алгоритмы: Полиномиальная смесь Дирихле (DMM) на конференции KDD2014, Тематическая модель Битерма (BTM) в журнале TKDE2016, Сетевая тематическая модель Word (WNTM) в журнале KAIS2018, Тематическая модель на основе псевдодокументов (PTM) на конференции KDD2016, Тематическая модель на основе самоагрегации (SATM) на конференции IJCAI2015, (ETM) на конференции PAKDD2017, Обобщенная модель полиномиальной смеси Дирихле (GPU-DMM) на основе обобщенной урны Поля (GPU) на конференции SIGIR2016, Generalized P´olya Urn (GPU)) основанная на Пуассоне модель полиномиальной смеси Дирихле (GPU-PDMM) в журнале TIS2017 и модель скрытых функций с DMM (LF-DMM) в журнале TACL2015. STTM также включает шесть корпусов коротких текстов для оценки. STTM представляет три аспекта оценки производительности алгоритмов (т. Е. Согласованность тем, кластеризацию и классификацию).
• Лекция, в которой рассматриваются некоторые из обозначений в этой статье: LDA и видео по тематическому моделированию Лекция Дэвида Блея или та же лекция на YouTube
• Д. Библиография Mimno LDA Исчерпывающий список ресурсов, связанных с LDA (включая документы и некоторые реализации)
• Gensim, Python + NumPy реализация онлайн-LDA для входных данных, превышающих доступную RAM.
• topicmodels и lda - это два пакета R для анализа LDA.
• «Анализ текста с помощью R», включая методы LDA, видеопрезентация для Октябрь 2011 г. Встреча группы пользователей R в Лос-Анджелесе
• MALLET Пакет на основе Java с открытым исходным кодом от Массачусетского университета в Амхерсте для тематического моделирования с помощью LDA, также имеет независимо разработанный графический интерфейс, инструмент тематического моделирования
• LDA в Mahout реализация LDA с использованием MapReduce на платформе Hadoop
• Руководство по скрытому распределению Дирихле (LDA) для платформы машинных вычислений Infer.NET Microsoft Research C # Machine Learning Framework
• LDA в Spark : Начиная с версии 1.3.0, Apache Spark также включает реализацию LDA
• LDA, exampleLDA Реализация MATLAB