Конические координаты

редактировать

Координатные поверхности конических координат. Константы b и c были выбраны равными 1 и 2 соответственно. Красная сфера представляет r = 2, синий эллиптический конус, выровненный по вертикальной оси z, представляет μ = ch (1), а желтый эллиптический конус, выровненный по (зеленой) оси x, соответствует ν = 2/3. Три поверхности пересекаются в точке P (показанной черной сферой) с декартовыми координатами примерно (1,26, -0,78, 1,34). Эллиптические конусы пересекают сферу в виде кривых в форме тако.

Конические координаты - это трехмерная ортогональная система координат, состоящая из концентрических сфер (описываемых их радиусом r) и двумя семействами перпендикулярных конусов, выровненных по осям z и x соответственно.

Содержание

1 Основные определения
2 Масштабные коэффициенты
3 Координаты светового конуса
4 Ссылки
5 Библиография
6 Внешние ссылки

Основные определения

Конические координаты $(r, μ, ν) {\ displaystyle (r, \ mu, \ nu)}$ $(r, \ mu, \ nu)$ определяются как

x = r μ ν bc {\ displaystyle x = {\ гидроразрыва {r \ mu \ nu} {bc}}}

x = \ frac {r \ mu \ nu} {bc}

y = rb (μ 2 - b 2) (ν 2 - b 2) (b 2 - c 2) {\ displaystyle y = {\ frac {r} {b}} {\ sqrt {\ frac {\ left (\ mu ^ {2} -b ^ {2} \ right) \ left (\ nu ^ {2} -b ^ {2} \ right) } {\ left (b ^ {2} -c ^ {2} \ right)}}}}

y = \ frac {r} {b} \ sqrt {\ frac {\ left (\ mu ^ {2} - b ^ {2} \ right) \ left (\ nu ^ {2} - b ^ {2} \ righ t)} {\ left (b ^ {2} - c ^ {2} \ right)}}

z = rc (μ 2 - c 2) (ν 2 - c 2) (c 2 - b 2) {\ displaystyle z = {\ frac {r} {c}} {\ sqrt {\ frac {\ left (\ mu ^ {2} -c ^ {2} \ right) \ left (\ nu ^ {2} - c ^ {2} \ right)} {\ left (c ^ {2} -b ^ {2} \ right)}}}}

z = \ frac {r} {c} \ sqrt {\ frac {\ left (\ mu ^ {2} - c ^ {2} \ right) \ left (\ nu ^ {2} - c ^ {2} \ right)} {\ left (c ^ {2} - b ^ {2} \ right)}}

со следующими ограничениями на координаты

ν 2 < c 2 < μ 2 < b 2. {\displaystyle \nu ^{2}

{\ displaystyle \ nu ^ {2} <c ^ {2} <\ mu ^ {2} <b ^ {2}.}

Поверхности константы r - это сферы с таким радиусом с центром в начале координат

x 2 + y 2 + z 2 = r 2, {\ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2},}

{\ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2},}

, тогда как поверхности с константой $μ {\ displaystyle \ mu}$ $\ mu$ и $ν {\ displaystyle \ nu}$ $\ nu$ - взаимно перпендикулярные конусы

x 2 μ 2 + y 2 μ 2 - b 2 + z 2 μ 2 - c 2 = 0 {\ displaystyle {\ frac {x ^ {2}} {\ mu ^ {2}}} + {\ frac {y ^ {2}} {\ mu ^ {2} -b ^ {2}}} + {\ frac {z ^ { 2}} {\ mu ^ {2} -c ^ {2}}} = 0}

{\ displaystyle {\ frac {x ^ {2}} {\ mu ^ {2}}} + {\ frac {y ^ {2}} { \ mu ^ {2} -b ^ {2}}} + {\ frac {z ^ {2}} {\ mu ^ {2} -c ^ {2}}} = 0}

x 2 ν 2 + y 2 ν 2 - b 2 + z 2 ν 2 - c 2 = 0. {\ displaystyle {\ frac {x ^ {2}} {\ nu ^ {2}}} + {\ frac {y ^ {2}} {\ nu ^ {2} -b ^ {2}}} + {\ frac {z ^ {2}} {\ nu ^ {2} -c ^ {2}}} = 0.}

{ \ displaystyle {\ frac {x ^ {2}} {\ nu ^ {2}}} + {\ frac {y ^ {2}} {\ nu ^ {2} -b ^ {2}}} + {\ гидроразрыв {z ^ {2}} {\ nu ^ {2} -c ^ {2}}} = 0.}

В этой системе координат и уравнение Лапласа, и Уравнение Гельмгольца разделимо.

Масштабные коэффициенты

Масштабный коэффициент для радиуса r равен единице (h r = 1), как в сферических координатах. Масштабные коэффициенты для двух конических координат равны

h μ = r μ 2 - ν 2 (b 2 - μ 2) (μ 2 - c 2) {\ displaystyle h _ {\ mu} = r {\ sqrt {\ гидроразрыв {\ mu ^ {2} - \ nu ^ {2}} {\ left (b ^ {2} - \ mu ^ {2} \ right) \ left (\ mu ^ {2} -c ^ {2} \ right)}}}}

h _ {\ mu} = r \ sqrt {\ frac {\ mu ^ {2} - \ nu ^ { 2}} {\ left (b ^ {2} - \ mu ^ {2} \ right) \ left (\ mu ^ {2} - c ^ {2} \ right)}}

h ν = r μ 2 - ν 2 (b 2 - ν 2) (c 2 - ν 2). {\ displaystyle h _ {\ nu} = r {\ sqrt {\ frac {\ mu ^ {2} - \ nu ^ {2}} {\ left (b ^ {2} - \ nu ^ {2} \ right) \ left (c ^ {2} - \ nu ^ {2} \ right)}}}.}

{\ displaystyle h _ {\ nu} = r {\ sqrt {\ frac {\ mu ^ {2} - \ nu ^ {2}} {\ left (b ^ {2} - \ nu ^ {2} \ right) \ left (c ^ {2} - \ nu ^ { 2} \ right)}}}.}

Конические координаты светового конуса

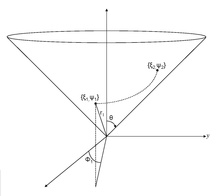
Был получен альтернативный набор (неортогональных) конических координат

$ξ знак равно р соз ⁡ (ϕ грех ⁡ θ) ψ = р грех ⁡ (ϕ грех ⁡ θ) ζ = θ, {\ Displaystyle {\ begin {выровнено} \ xi = r \ cos (\ phi \ sin \ theta) \\\ psi = r \ sin (\ phi \ sin \ theta) \\\ zeta = \ theta, \ end {align}}}$ ${\ displaystyle {\ begin {align} \ xi = r \ cos (\ phi \ sin \ theta) \\\ psi = r \ sin (\ phi \ sin \ theta) \\\ zeta = \ thet а, \ конец {выровнено}}}$

где ${r, θ, ϕ} {\ displaystyle \ {r, \ theta, \ phi \}}$ ${\ displaystyle \ {r, \ theta, \ phi \}}$ - сферические полярные координаты. Соответствующие обратные соотношения следующие:

$r = ξ 2 + ψ 2 ϕ = 1 sin ⁡ ζ arctan ⁡ (ψ ξ) θ = ζ. {\ displaystyle {\ begin {align} r = {\ sqrt {\ xi ^ {2} + \ psi ^ {2}}} \\\ phi = {\ frac {1} {\ sin \ zeta}} \ arctan ({\ frac {\ psi} {\ xi}}) \\\ theta = \ zeta. \ end {align}}}$ ${\ displaystyle {\ begin {align} r = {\ sqrt {\ xi ^ {2} + \ psi ^ {2}}} \\\ phi = {\ frac {1} {\ sin \ zeta}} \ arctan ( {\ frac {\ psi} {\ xi}}) \\\ theta = \ zeta. \ end {align}}}$

Бесконечно малое евклидово расстояние между двумя точками в этих координатах

ds 2 = d ξ 2 + d ψ 2 + (ξ 2 + ψ 2) (1 + arctan ⁡ (ψ ξ) 2 детская кроватка ⁡ ζ 2) d ζ 2 + 2 ψ arctan ⁡ (ψ ξ) детская кроватка ⁡ ζ d ξ d ζ - 2 ξ arctan ⁡ (ψ ξ) кроватка ⁡ ζ d ψ d ζ. {\ displaystyle {\ begin {align} ds ^ {2} = d \ xi ^ {2} + d \ psi ^ {2} + (\ xi ^ {2} + \ psi ^ {2}) (1+ \ arctan ({\ frac {\ psi} {\ xi}}) ^ {2} \ cot \ zeta ^ {2}) d \ zeta ^ {2} \\ + 2 \ psi \ arctan ({\ frac { \ psi} {\ xi}}) \ cot \ zeta d \ xi d \ zeta -2 \ xi \ arctan ({\ frac {\ psi} {\ xi}}) \ cot \ zeta d \ psi d \ zeta. \ end {align}}}

{\ displaystyle {\ begin {align} ds ^ {2} = d \ xi ^ {2} + d \ psi ^ {2} + (\ xi ^ {2} + \ psi ^ {2}) (1+ \ arctan ({\ frac {\ psi} {\ xi}}) ^ {2} \ cot \ zeta ^ {2}) d \ zeta ^ {2} \\ + 2 \ psi \ arctan ({ \ frac {\ psi} {\ xi}}) \ cot \ zeta d \ xi d \ zeta -2 \ xi \ arctan ({\ frac {\ psi} {\ xi}}) \ cot \ zeta d \ psi d \ zeta. \ end {align}}}

$ξ {\ displaystyle \ xi}$ $\ xi$ и $ψ {\ displaystyle \ psi}$ $\ psi$ - ортогональные координаты на поверхности заданного конуса по $ζ = π 4 {\ displaystyle \ zeta = {\ frac {\ pi} {4}}}$ ${\ displaystyle \ zeta = {\ frac {\ pi} {4}}}$ . Если путь между любыми двумя точками ограничен этой поверхностью, то геодезическое расстояние между любыми двумя точками

${ξ 1, ψ 1, ζ 1 = π 4} {\ displaystyle \ {\ xi _ {1}, \ psi _ {1}, \ zeta _ {1} = {\ frac {\ pi} {4}} \}}$ ${\ displaystyle \ {\ xi _ {1}, \ psi _ {1}, \ zeta _ {1 } = {\ frac {\ pi} {4}} \}}$ и ${ξ 2, ψ 2, ζ 2 = π 4} {\ displaystyle \ {\ xi _ {2}, \ psi _ {2}, \ zeta _ {2} = {\ frac {\ pi} {4}} \}}$ ${\ displaystyle \ {\ xi _ {2}, \ psi _ {2}, \ zeta _ {2} = {\ frac {\ pi} {4}} \}}$ равно

$s 12 2 = (ξ 1 - ξ 2) 2 + (ψ 1 - ψ 2) 2. {\ Displaystyle s_ {12} ^ {2} = (\ xi _ {1} - \ xi _ {2}) ^ {2} + (\ psi _ {1} - \ psi _ {2}) ^ {2 }.}$ ${\ displaystyle s_ {12} ^ {2} = (\ xi _ {1} - \ xi _ {2}) ^ {2} + (\ psi _ {1} - \ psi _ {2}) ^ {2}.}$

Ссылки

Библиография

Morse PM, Feshbach H (1953). Методы теоретической физики, часть I. Нью-Йорк: МакГроу-Хилл. п. 659. ISBN 0-07-043316-X. LCCN 52011515.
Margenau H, Murphy GM (1956). Математика физики и химии. Нью-Йорк: Д. ван Ностранд. Стр. 183 –184. LCCN 55010911.
Корн Г.А., Корн TM (1961). Математический справочник для ученых и инженеров. Нью-Йорк: Макгроу-Хилл. п. 179. LCCN 59014456. ASIN B0000CKZX7.
Зауэр Р., Сабо I (1967). Mathematische Hilfsmittel des Ingenieurs. Нью-Йорк: Springer Verlag. С. 991–100. LCCN 67025285.
Arfken G (1970). Математические методы для физиков (2-е изд.). Орландо, Флорида: Academic Press. С. 118–119. ASIN B000MBRNX4.
Мун П., Спенсер Д.Е. (1988). «Конические координаты (r, θ, λ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд., 3-е изд.). Нью-Йорк: Springer-Verlag. С. 37–40 (Таблица 1.09). ISBN 978-0-387-18430-2.

Внешние ссылки

Описание MathWorld конических координат