Поверхность Шерка

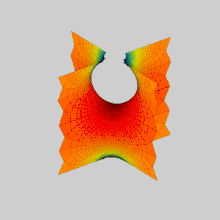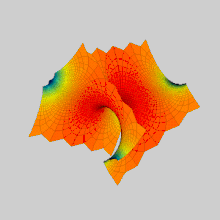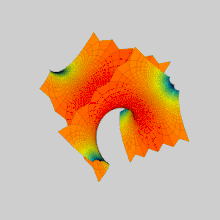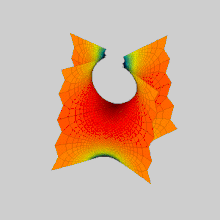
Анимация преобразования первой и второй поверхностей Шерка друг в друга: они являются членами одного ассоциированного семейства минимальных поверхностей.

В математике, a Поверхность Шерка (названная в честь Генриха Шерка ) является примером минимальной поверхности. Шерк описал две полные вложенные минимальные поверхности в 1834 году; его первая поверхность - двоякопериодическая, вторая - однокнопериодическая. Они были третьими нетривиальными примерами минимальных поверхностей (первыми двумя были катеноид и геликоид ). Две поверхности являются сопряженными друг другу.

Поверхности Шерка возникают при изучении некоторых предельных задач минимальной поверхности и при изучении гармонических диффеоморфизмов гиперболического пространства.

• 1 Первая поверхность Шерка
  • 1.1 Построение простой поверхности Шерка
  • 1.2 Более общие поверхности Шерка
• 2 Вторая поверхность Шерка
• 3 Внешние ссылки
• 4 Ссылки

Первая поверхность Шерка - это асимптотика двух бесконечных семейств параллельных плоскостей, ортогональных друг другу, которые пересекаются около z = 0 в шахматной доске соединяющих арок. Он содержит бесконечное количество прямых вертикальных линий.

Построение простой поверхности Шерка

STL элементарная ячейка первой поверхности Шерка Пять элементарных ячеек, помещенных вместе

Рассмотрим следующую задачу о минимальной поверхности на квадрате в евклидовой плоскости : для натурального числа n найти минимальную поверхность Σ n как график некоторой функции

$un:\; (-\; \pi \; 2,\; +\; \pi \; 2)\; \times \; (-\; \pi \; 2,\; +\; \pi \; 2)\; \to \; R\; \{\backslash \; displaystyle\; u\_\; \{n\}:\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\},\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; times\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\},\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; to\; \backslash \; mathbb\; \{R\}\}$

таким, что

То есть u n удовлетворяет уравнению минимальной поверхности

$div\; (\nabla \; un\; (x,\; y)\; 1\; +\; |\; \nabla \; un\; (x,\; y)\; |\; 2)\; \equiv \; 0\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{div\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; nabla\; u\_\; \{n\}\; (x,\; y)\}\; \{\backslash \; sqrt\; \{1+\; |\; \backslash \; nabla\; u\_\; \{n\}\; (x,\; y)\; |\; ^\; \{2\}\}\}\}\; \backslash \; right)\; \backslash \; эквив\; 0\}$

и

Что, если вообще есть, является предельной поверхностью, когда n стремится к бесконечности? Ответ дал Х. Шерк в 1834 году: предельная поверхность Σ - это график

$u:\; (-\; \pi \; 2,\; +\; \pi \; 2)\; \times \; (-\; \pi \; 2,\; +\; \pi \; 2)\; \to \; R,\; \{\backslash \; displaystyle\; u\; :\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\},\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; times\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\},\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; to\; \backslash \; mathbb\; \{R\},\}$

$u\; (x,\; y)\; =\; log\; \; (cos\; \; (x)\; cos\; \; (y)).\; \{\backslash \; displaystyle\; u\; (x,\; y)\; =\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; cos\; (x)\}\; \{\backslash \; cos\; (y)\}\}\; \backslash \; right).\}$

То есть поверхность Шерка над квадратом:

Более общие поверхности Шерка

Можно рассматривать аналогичные задачи с минимальной поверхностью на других четырехугольниках в евклидовой плоскости. Можно также рассмотреть ту же задачу на четырехугольниках в гиперболической плоскости . В 2006 году Гарольд Розенберг и Паскаль Коллин использовали гиперболические поверхности Шерка для построения гармонического диффеоморфизма комплексной плоскости на гиперболическую плоскость (единичный круг с гиперболической метрикой), тем самым опровергнув гипотезу Шена – Яу.

вторая поверхность Шерка элементарная ячейка STL второй поверхности Шерка

Вторая поверхность Шерка глобально выглядит как две ортогональные плоскости, пересечение которых состоит из последовательности туннелей в чередующихся направлениях. Его пересечения с горизонтальными плоскостями состоят из чередующихся гипербол.

Он имеет неявное уравнение:

$sin\; \; (z)\; -\; sinh\; \; (x)\; sinh\; \; (y)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; sin\; (z)\; -\; \backslash \; sinh\; (x)\; \backslash \; sinh\; (y)\; =\; 0\}$

Он имеет параметризацию Вейерштрасса – Эннепера $f\; (z)\; =\; 4\; 1\; -\; z\; 4\; \{\backslash \; displaystyle\; f\; (z)\; =\; \{\backslash \; frac\; \{4\}\; \{1-\; z\; ^\; \{4\}\}\}\}$, $g\; (z)\; =\; iz\; \{\backslash \; displaystyle\; g\; (z)\; =\; iz\}$и может быть параметризовано как:

$x\; (r,\; \theta )\; =\; 2\; \Re \; (пер\; \; (1\; +\; рей\; \theta )\; -\; пер\; \; (1\; -\; рей\; \theta ))\; =\; пер\; \; (1\; +\; r\; 2\; +\; 2\; r\; соз\; \; \theta \; 1\; +\; r\; 2-2\; r\; соз\; \; \theta )\; \{\backslash \; displaystyle\; x\; (\; r,\; \backslash \; theta)\; =\; 2\; \backslash \; Re\; (\backslash \; ln\; (1\; +\; re\; ^\; \{i\; \backslash \; theta\})\; -\; \backslash \; ln\; (1-re\; ^\; \{i\; \backslash \; theta\}))\; =\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1+\; r\; ^\; \{2\}\; +\; 2r\; \backslash \; cos\; \backslash \; theta\}\; \{1\; +\; r\; ^\; \{2\}\; -2r\; \backslash \; cos\; \backslash \; theta\}\}\; \backslash \; right)\}$

$y\; (r,\; \theta )\; =\; \Re \; (4\; i\; tan\; -\; 1\; \; (рей\; \theta ))\; знак\; равно\; пер\; \; (1\; +\; р\; 2\; -\; 2\; р\; грех\; \; \theta \; 1\; +\; р\; 2\; +\; 2\; р\; грех\; \; \theta )\; \{\backslash \; Displaystyle\; у\; (г,\; \backslash \; тета)\; =\; \backslash \; Re\; (4i\; \backslash \; tan\; ^\; \{-\; 1\}\; (re\; ^\; \{i\; \backslash \; theta\}))\; =\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\; +\; r\; ^\; \{2\}\; -2r\; \backslash \; sin\; \backslash \; theta\}\; \{1\; +\; r\; ^\; \{2\}\; +\; 2r\; \backslash \; sin\; \backslash \; theta\; \}\}\; \backslash \; right)\}$

$z\; (r,\; \theta )\; =\; \Re \; (2\; i\; (-\; ln\; \; (1\; -\; r\; 2\; e\; 2\; i\; \theta )\; +\; ln\; \; (1\; +\; r\; 2\; e\; 2\; i\; \theta ))\; =\; 2\; загар\; -\; 1\; \; (2\; р\; 2\; грех\; \; 2\; \theta \; р\; 4-1)\; \{\backslash \; Displaystyle\; Z\; (г,\; \backslash \; т\; heta)\; =\; \backslash \; Re\; (2i\; (-\; \backslash \; ln\; (1-r\; ^\; \{2\}\; e\; ^\; \{2i\; \backslash \; theta\})\; +\; \backslash \; ln\; (1\; +\; r\; ^\; \{2\}\; e\; ^\; \{2i\; \backslash \; theta\}))\; =\; 2\; \backslash \; tan\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{2r\; ^\; \{2\}\; \backslash \; sin\; 2\; \backslash \; theta\}\; \{r\; ^\; \{4\}\; -1\}\}\; \backslash \; right)\}$

для $\theta \; \in \; [0,\; 2\; \pi )\; \{\backslash \; displaystyle\; \backslash \; theta\; \backslash \; in\; [0,2\; \backslash \; pi)\}$и $r\; \in \; (0,\; 1)\; \{\backslash \; displaystyle\; r\; \backslash \; in\; (0,1)\}$. Это дает один период поверхности, который затем может быть расширен в направлении z за счет симметрии.

Поверхность была обобщена Х. Керхером в седловую башню семейство периодических минимальных поверхностей.

Как ни странно, в литературе эту поверхность иногда называют пятой поверхностью Шерка. Чтобы свести к минимуму путаницу, полезно называть ее однопериодической поверхностью Шерка или башней Шерка.

• Сабитов, И.Х. (2001) [1994], Энциклопедия математики, EMS Press
• Первая поверхность Шерка в ИИГС Geometry [2]
• Вторая поверхность Шерка в ИИГС Geometry [ 3]
• Минимальные поверхности Шерка в Mathworld [4]