Объединение соседей

Метод восходящей кластеризации для создания филогенетических деревьев

В биоинформатике, Объединение соседей - это восходящий (агломеративный) метод кластеризации для создания филогенетических деревьев, созданных и Масатоши Ней в 1987 году. Обычно используется для деревьев, основанных на данных ДНК или белка последовательности, алгоритм требует знания расстояния между каждой парой таксонов (например, видов или последовательностей) для формирования дерева.

Содержание

• 1 Алгоритм
  • 1.1 Q-матрица
  • 1.2 Расстояние от членов пары до нового узла
  • 1.3 Расстояние от других таксонов до новый узел
  • 1.4 Сложность
• 2 Пример
  • 2.1 Первый шаг
    • 2.1.1 Первое соединение
    • 2.1.2 Оценка длины первой ветви
    • 2.1.3 Первое обновление матрицы расстояний
  • 2.2 Второй этап
    • 2.2.1 Второе соединение
    • 2.2.2 Оценка длины второй ветви
    • 2.2.3 Второе расстояние Обновление матрицы ce
  • 2.3 Заключительный шаг
  • 2.4 Заключение: аддитивные расстояния
• 3 Объединение соседей как минимальная эволюция
• 4 Преимущества и недостатки
• 5 Реализации и варианты
• 6 См. также
• 7 Ссылки
  • 7.1 Другие источники
• 8 Внешние ссылки

Алгоритм

Начиная с звездообразного дерева (A), матрица Q вычисляется и используется для выбора пары узлов для объединения, в данном случае f и г. Они присоединяются к вновь созданному узлу u, как показано на (B). Часть дерева, показанная сплошными линиями, теперь зафиксирована и не будет изменена на последующих этапах соединения. Расстояния от узла u до узлов a-e вычисляются из уравнения (3). Затем этот процесс повторяется, используя матрицу только расстояний между узлами a, b, c, d, e и u и полученную из нее Q-матрицу. В этом случае u и e присоединяются к вновь созданному v, как показано на (C). Еще две итерации ведут сначала к (D), а затем к (E), после чего алгоритм завершается, поскольку дерево полностью разрешено.

Соединение соседей принимает в качестве входных данных матрицу расстояний, определяющую расстояние между каждой парой таксонов. Алгоритм начинается с полностью неразрешенного дерева, топология которого соответствует топологии звездообразной сети, и повторяется по следующим шагам, пока дерево не будет полностью разрешено и все длины ветвей не будут известны:

1. На основе текущая матрица расстояний вычислить матрицу $Q\; \{\backslash \; displaystyle\; Q\}$(определено ниже).
2. Найти пару различных таксонов i и j (т.е. с $i\; \ne \; j\; \{\backslash \; displaystyle\; i\; \backslash \; neq\; j\}$), для которого $Q\; (i,\; j)\; \{\backslash \; displaystyle\; Q\; (i,\; j)\}$имеет наименьшее значение. Эти таксоны присоединяются к вновь созданному узлу, который соединен с центральным узлом. На рисунке справа f и g присоединены к новому узлу u.
3. Вычислите расстояние от каждого из таксонов в паре до этого нового узла.
4. Рассчитайте расстояние от каждого таксона за пределами этой пары до нового узла.
5. Запустите алгоритм снова, заменив пару объединенных соседей новым узлом и используя расстояния, вычисленные на предыдущем шаге.

Q-матрица

На основе матрицы расстояний, относящейся к $n\; \{\backslash \; displaystyle\; n\}$таксонам, вычислите $Q\; \{\backslash \; displaystyle\; Q\}$следующим образом:

$Q\; (i,\; j)\; =\; (n\; -\; 2)\; d\; (i,\; j)\; -\; \sum \; k\; =\; 1\; nd\; (i,\; k)\; -\; \sum \; k\; =\; 1\; nd\; (j,\; k)\; \{\backslash \; Displaystyle\; Q\; (я,\; J)\; =\; (N-2)\; d\; (я,\; J)\; -\; \backslash \; сумма\; \_\; \{к\; =\; 1\}\; ^\; \{п\}\; d\; (я,\; к)\; -\; \backslash \; сумма\; \_\; \{к\; =\; 1\}\; ^\; \{п\; \}\; d\; (j,\; k)\}$

(1)

где $d\; (i,\; j)\; \{\backslash \; displaystyle\; d\; (i,\; j)\}$- расстояние между таксонами $i\; \{\backslash \; displaystyle\; i\}$и $j\; \{\backslash \; displaystyle\; j\}$.

Расстояние от членов пары до нового узла

Для каждого таксона в паре присоединился, используйте t Следующая формула для вычисления расстояния до нового узла:

$\delta \; (f,\; u)\; =\; 1\; 2\; d\; (f,\; g)\; +\; 1\; 2\; (n\; -\; 2)\; [\sum \; k\; =\; 1\; nd\; (f,\; k)\; -\; \sum \; К\; знак\; равно\; 1\; nd\; (g,\; k)]\; \{\backslash \; displaystyle\; \backslash \; delta\; (f,\; u)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; d\; (f,\; g)\; +\; \{\backslash \; frac\; \{1\}\; \{2\; (n-\; 2)\}\}\; \backslash \; left\; [\backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; d\; (f,\; k)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; d\; (g,\; k)\; \backslash \; right]\; \backslash \; quad\}$

(2)

и:

$\delta \; (g,\; u)\; =\; d\; (f,\; g)\; -\; \delta \; (f,\; u)\; \{\backslash \; displaystyle\; \backslash \; delta\; (g,\; u)\; =\; d\; (f,\; g)\; -\; \backslash \; delta\; (f,\; u)\; \backslash \; quad\}$

Таксоны $f\; \{\backslash \; displaystyle\; f\}$и $g\; \{\backslash \; displaystyle\; g\}$являются парными таксоны, а $u\; \{\backslash \; displaystyle\; u\}$- вновь созданный узел. Ветви, соединяющие $f\; \{\backslash \; displaystyle\; f\}$и $u\; \{\backslash \; displaystyle\; u\}$и $g\; \{\backslash \; displaystyle\; g\}$и $u\; \{\backslash \; displaystyle\; u\}$, и их длины, $\delta \; (f,\; u)\; \{\backslash \; displaystyle\; \backslash \; delta\; (f,\; u)\}$и $\delta \; (g,\; u)\; \{\backslash \; displaystyle\; \backslash \; delta\; (g,\; u)\}$являются частью дерева, которое постепенно создается; они не влияют и не влияют на последующие шаги присоединения соседей.

Расстояние других таксонов от нового узла

Для каждого таксона, не рассмотренного на предыдущем шаге, мы вычисляем расстояние до нового узла следующим образом:

$d\; (u,\; k)\; =\; 1\; 2\; [d\; (f,\; k)\; +\; d\; (g,\; k)\; -\; d\; (f,\; g)]\; \{\backslash \; displaystyle\; d\; (u,\; k)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [d\; (f,\; k)\; +\; d\; (g,\; k)\; -d\; (f,\; g)]\}$

(3)

где $u\; \{\backslash \; displaystyle\; u\}$- новый узел, $k\; \{\backslash \; displaystyle\; k\}$- узел, расстояние до которого мы хотим вычислить, и $f\; \{\backslash \; displaystyle\; f\}$и $g\; \{\backslash \; displaystyle\; g\; \}$- это только что присоединившиеся члены пары.

Сложность

Соединение соседей в наборе из $n\; \{\backslash \; displaystyle\; n\}$таксонов требует $n\; -\; 3\; \{\backslash \; displaystyle\; n-3\}$итераций. На каждом шаге нужно построить и найти матрицу $Q\; \{\backslash \; displaystyle\; Q\}$. Первоначально матрица $Q\; \{\backslash \; displaystyle\; Q\}$имеет размер $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$, затем следующий шаг - $(n\; -\; 1)\; \times \; (n\; -\; 1)\; \{\backslash \; displaystyle\; (n-1)\; \backslash \; times\; (n-1)\}$и т. д. Прямая реализация этого приводит к алгоритму с временной сложностью из $О\; (n\; 3)\; \{\backslash \; displaystyle\; O\; (n\; ^\; \{3\})\}$; Существуют реализации, которые используют эвристику для достижения более высоких результатов в среднем.

Пример

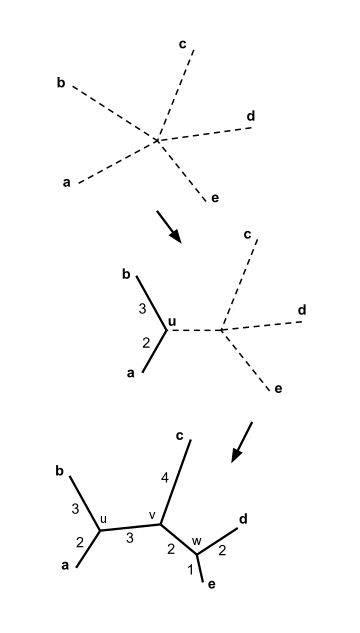
Соединение соседей с 5 таксонами. В этом случае 2 шага соединения соседей дают дерево с полностью разрешенной топологией. Ветви получившегося дерева помечены своей длиной.

Предположим, что у нас есть пять таксонов $(a,\; b,\; c,\; d,\; e)\; \{\backslash \; displaystyle\; (a,\; b,\; c,\; d,\; e)\}$и следующая матрица расстояний $D\; \{\backslash \; displaystyle\; D\}$:

	a	b	c	d	e
a	0	5	9	9	8
b	5	0	10	10	9
c	9	10	0	8	7
d	9	10	8	0	3
e	8	9	7	3	0

Первый шаг

Первое объединение

Мы вычисляем значения $Q\; 1\; \{\backslash \; displaystyle\; Q\_\; \{1\}\}$по уравнению (1). Например:

$Q\; 1\; (a,\; b)\; =\; (n\; -\; 2)\; d\; (a,\; b)\; -\; \sum \; k\; =\; 1\; 5\; d\; (a,\; k)\; -\; \sum \; k\; =\; 1\; 5\; d\; (b,\; k)\; \{\; \backslash \; Displaystyle\; Q\_\; \{1\}\; (a,\; b)\; =\; (n-2)\; d\; (a,\; b)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{5\}\; d\; (a,\; k)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\; \}\; ^\; \{5\}\; d\; (b,\; k)\}$

$=\; (5\; -\; 2)\; \times \; 5\; -\; (5\; +\; 9\; +\; 9\; +\; 8)\; -\; (5\; +\; 10\; +\; 10\; +\; 9)\; =\; 15\; -\; 31\; -\; 34\; =\; -\; 50\; \{\backslash \; displaystyle\; =\; (5-2)\; \backslash \; times\; 5-\; (5\; +\; 9\; +\; 9\; +\; 8)\; -\; (5\; +\; 10\; +\; 10\; +\; 9)\; =\; 15-31-34\; =\; -50\}$

Получаем следующие значения для матрицы $Q\; 1\; \{\backslash \; displaystyle\; Q\_\; \{1\}\}$(диагональные элементы матрицы не используются и здесь опускаются):

	a	b	c	d	e
a		−50	−38	−34	−34
b	−50		−38	−34	−34
c	−38	-38		-40	-40
d	-34	-34	-40		-48
e	−34	−34	−40	−48

В приведенном выше примере $Q\; 1\; (a,\; b)\; =\; -\; 50\; \{\backslash \; displaystyle\; Q\_\; \{1\}\; (a,\; b)\; =\; -\; 50\}$. Это наименьшее значение из $Q\; 1\; \{\backslash \; displaystyle\; Q\_\; \{1\}\}$, поэтому мы объединяем элементы $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$.

Оценка длины первой ветви

Пусть $u\; \{\backslash \; displaystyle\; u\}$обозначает новый узел. По уравнению (2), приведенному выше, ветви, соединяющие $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$с $u\; \{\; \backslash \; displaystyle\; u\}$тогда имеет длины:

$\delta \; (a,\; u)\; =\; 1\; 2\; d\; (a,\; b)\; +\; 1\; 2\; (5–2)\; [\sum \; k\; =\; 1\; 5\; d\; (a,\; к)\; -\; \sum \; К\; знак\; равно\; 1\; 5\; d\; (b,\; k)]\; =\; 5\; 2\; +\; 31\; -\; 34\; 6\; =\; 2\; \{\backslash \; displaystyle\; \backslash \; delta\; (a,\; u)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; d\; (a,\; б)\; +\; \{\backslash \; frac\; \{1\}\; \{2\; (5-2)\}\}\; \backslash \; left\; [\backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{5\}\; d\; (a,\; k)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\; 5\}\; d\; (b,\; k)\; \backslash \; right]\; \backslash \; quad\; =\; \{\backslash \; frac\; \{5\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{31-34\}\; \{6\}\}\; =\; 2\}$

$\delta \; (b,\; u)\; =\; d\; (a,\; b)\; -\; \delta \; (a,\; u)\; знак\; равно\; 5-2\; =\; 3\; \{\backslash \; displaystyle\; \backslash \; delta\; (b,\; u)\; =\; d\; (a,\; b)\; -\; \backslash \; delta\; (a,\; u)\; \backslash \; quad\; =\; 5-2\; =\; 3\}$

Первое обновление матрицы расстояний

Затем мы переходим к обновлению исходной матрицы расстояний $D\; \{\backslash \; displaystyle\; D\}$в новую матрицу расстояний $D\; 1\; \{\backslash \; displaystyle\; D\_\; \{1\}\}$(см. ниже), уменьшен в размере на одну строку и один столбец из-за объединения $a\; \{\backslash \; displaystyle\; a\}$с $b\; \{\backslash \; displaystyle\; b\}$в своего соседа $u\; \{\backslash \; displaystyle\; u\}$. Используя приведенное выше уравнение (3), мы вычисляем расстояние от $u\; \{\backslash \; displaystyle\; u\}$до каждого из других узлов, кроме $a\; \{\backslash \; displaystyle\; a\}$<222.>и $b\; \{\backslash \; displaystyle\; b\}$. В этом случае получаем:

$d\; (u,\; c)\; =\; 1\; 2\; [d\; (a,\; c)\; +\; d\; (b,\; c)\; -\; d\; (a,\; b)]\; =\; 9\; +\; 10\; -\; 5\; 2\; =\; 7\; \{\backslash \; displaystyle\; d\; (u,\; c)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [d\; (a,\; c)\; +\; d\; (b,\; c)\; -d\; (a,\; b)]\; =\; \{\backslash \; frac\; \{9\; +\; 10\; -5\}\; \{2\}\}\; =\; 7\}$

$d\; (u,\; d)\; =\; 1\; 2\; [d\; (a,\; d)\; +\; d\; (b,\; d)\; -\; d\; (a,\; b)]\; =\; 9\; +\; 10\; -\; 5\; 2\; =\; 7\; \{\backslash \; Displaystyle\; d\; (u,\; d)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [d\; (a,\; d)\; +\; d\; (b,\; d)\; -d\; (a,\; b)]\; =\; \{\backslash \; frac\; \{\; 9\; +\; 10-5\}\; \{2\}\}\; =\; 7\}$

$d\; (u,\; e)\; =\; 1\; 2\; [d\; (a,\; e)\; +\; d\; (b,\; e)\; -\; d\; (a,\; b)]\; =\; 8\; +\; 9–5\; 2\; =\; 6\; \{\backslash \; Displaystyle\; d\; (u,\; e)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [d\; (a,\; e)\; +\; d\; (b,\; e)\; -d\; (a,\; b)]\; =\; \{\; \backslash \; frac\; \{8\; +\; 9-5\}\; \{2\}\}\; =\; 6\}$

Результирующая матрица расстояний $D\; 1\; \{\backslash \; displaystyle\; D\_\; \{1\}\}$:

	u	c	d	e
u	0	7	7	6
c	7	0	8	7
d	7	8	0	3
e	6	7	3	0

Значения жирным шрифтом в $D\; 1\; \{\backslash \; displaystyle\; D\_\; \{1\}\}$соответствуют вновь вычисленным расстояниям, тогда как значения, выделенные курсивом, не зависят от обновления матрицы, поскольку они соответствуют расстояниям между элементами, не участвующими в первом соединении таксоны.

Второй шаг

Второе объединение

Соответствующая матрица $Q\; 2\; \{\backslash \; displaystyle\; Q\_\; \{2\}\}$:

	u	c	d	e
u		- 28	-24	-24
c	-28		-24	-24
d	-24	-24		−28
e	−24	−24	−28

Мы можем выбрать либо присоединение к $u\; \{\backslash \; displaystyle\; u\}$и $с\; \{\backslash \; displaystyle\; c\}$, или для объединения $d\; \{\backslash \; displaystyle\; d\}$и $e\; \{\backslash \; displaystyle\; e\}$; обе пары имеют минимальное значение $Q\; 2\; \{\backslash \; displaystyle\; Q\_\; \{2\}\}$от $-\; 28\; \{\backslash \; displaystyle\; -28\}$, и любой выбор приводит к тот же результат. Для конкретности соединим $u\; \{\backslash \; displaystyle\; u\}$и $c\; \{\backslash \; displaystyle\; c\}$и назовем новый узел $v\; \{\backslash \; displaystyle\; v\; \}$.

Оценка длины второй ветви

Длины ветвей, соединяющих $u\; \{\backslash \; displaystyle\; u\}$и $c\; \{\backslash \; displaystyle\; c\}$до $v\; \{\backslash \; displaystyle\; v\}$можно вычислить:

$\delta \; (u,\; v)\; =\; 1\; 2\; d\; (u,\; c)\; +\; 1\; 2\; (4–2)\; [\sum \; k\; Знак\; равно\; 1\; 4\; d\; (u,\; К)\; -\; \sum \; К\; знак\; равно\; 1\; 4\; d\; (c,\; k)]\; =\; 7\; 2\; +\; 20\; -\; 22\; 4\; =\; 3\; \{\backslash \; displaystyle\; \backslash \; delta\; (u,\; v)\; =\; \{\backslash \; frac\; \{1\}\; \{\; 2\}\}\; d\; (u,\; c)\; +\; \{\backslash \; frac\; \{1\}\; \{2\; (4-2)\}\}\; \backslash \; left\; [\backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{4\}\; d\; (u,\; k)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{4\}\; d\; (c,\; k)\; \backslash \; right]\; \backslash \; quad\; =\; \{\backslash \; frac\; \{7\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{20-22\}\; \{4\}\}\; =\; 3\}$

$\delta \; (c,\; v)\; знак\; равно\; d\; (u,\; c)\; -\; \delta \; (u,\; v)\; =\; 7-3\; =\; 4\; \{\backslash \; displaystyle\; \backslash \; delta\; (c,\; v)\; =\; d\; (u,\; c)\; -\; \backslash \; delta\; (u,\; v)\; \backslash \; quad\; =\; 7-3\; =\; 4\}$

Объединение элементов и вычисление длины ответвления помогает нарисовать дерево соединения соседей, как показано на рисунке.

Второе обновление матрицы расстояний

Обновленная матрица расстояний $D\; 2\; \{\backslash \; displaystyle\; D\_\; \{2\}\; \}$для остальных трех узлов: $v\; \{\backslash \; displaystyle\; v\}$, $d\; \{\backslash \; displaystyle\; d\}$и $e\; \{\backslash \; displaystyle\; e\}$, теперь вычисляется:

$d\; (v,\; d)\; =\; 1\; 2\; [d\; (u,\; d)\; +\; d\; (c,\; d)\; -\; d\; (u,\; c)]\; =\; 7\; +\; 8\; -\; 7\; 2\; Знак\; равно\; 4\; \{\backslash \; displaystyle\; d\; (v,\; d)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [d\; (u,\; d)\; +\; d\; (c,\; d)\; -d\; (u,\; c)]\; =\; \{\backslash \; frac\; \{7\; +\; 8-7\}\; \{2\}\}\; =\; 4\}$

$d\; (v,\; e)\; =\; 1\; 2\; [d\; (u,\; e)\; +\; d\; (c,\; e)\; -\; d\; (u,\; c)]\; =\; 6\; +\; 7\; -\; 7\; 2\; =\; 3\; \{\backslash \; Displaystyle\; d\; (v,\; e)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [d\; (u,\; e)\; +\; d\; (c,\; e)\; -d\; (u,\; c)]\; =\; \{\backslash \; frac\; \{6\; +\; 7-7\}\; \{2\}\}\; =\; 3\}$

	v	d	e
v	0	4	3
d	4	0	3
e	3	3	0

Заключительный шаг

На этом этапе топология дерева полностью определена. Однако для ясности мы можем вычислить матрицу $Q\; 3\; \{\backslash \; displaystyle\; Q\_\; \{3\}\}$. Например:

$Q\; 3\; (v,\; e)\; =\; (3\; -\; 2)\; d\; (v,\; e)\; -\; \sum \; k\; =\; 1\; 3\; d\; (v,\; k)\; -\; \sum \; k\; =\; 1\; 3\; d\; (e,\; k)\; =\; 3\; -\; 7\; -\; 6\; =\; -\; 10\; \{\backslash \; Displaystyle\; Q\_\; \{3\}\; (v,\; e)\; =\; (3-2)\; d\; (v,\; e)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{3\}\; d\; (v,\; k)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{3\}\; d\; (e,\; k)\; =\; 3-7-6\; =\; -10\}$

	v	d	e
v		−10	−10
d	−10		−10
e	−10	−10

Для конкретности соединим $v\; \{\backslash \; displaystyle\; v\}$и $d\; \{\backslash \; displaystyle\; d\}$и вызовите последний узел $w\; \{\backslash \; displaystyle\; w\}$. Длины трех оставшихся ветвей можно вычислить:

$\delta \; (v,\; w)\; =\; 1\; 2\; d\; (v,\; d)\; +\; 1\; 2\; (3\; -\; 2)\; [\sum \; k\; =\; 1\; 3\; d\; (v,\; k)\; -\; \sum \; К\; знак\; равно\; 1\; 3\; d\; (d,\; k)]\; =\; 4\; 2\; +\; 7\; -\; 7\; 2\; =\; 2\; \{\backslash \; displaystyle\; \backslash \; delta\; (v,\; w)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; d\; (v,\; d)\; +\; \{\backslash \; frac\; \{1\}\; \{2\; (3-2)\}\}\; \backslash \; left\; [\backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{3\}\; d\; (v,\; k)\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{3\}\; d\; (d,\; k)\; \backslash \; right]\; \backslash \; quad\; =\; \{\backslash \; frac\; \{4\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{7-7\}\; \{2\}\}\; =\; 2\}$

$\delta \; (w,\; d)\; =\; d\; (v,\; d)\; -\; \delta \; (v,\; w)\; знак\; равно\; 4\; -\; 2\; =\; 2\; \{\backslash \; displaystyle\; \backslash \; delta\; (w,\; d)\; =\; d\; (v,\; d)\; -\; \backslash \; delta\; (v,\; w)\; =\; 4-2\; =\; 2\}$

$\delta \; (вес,\; е)\; знак\; равно\; d\; (v,\; е)\; -\; \delta \; (v,\; w)\; =\; 3\; -\; 2\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; delta\; (w,\; e)\; =\; d\; (v,\; e)\; -\; \backslash \; delta\; (v,\; w)\; =\; 3-2\; =\; 1\}$

Теперь дерево соединения соседей завершено, как показано на рисунке.

Заключение: аддитивные расстояния

Этот пример представляет идеализированный случай: обратите внимание, что если мы перейдем от одного таксона к любому другому по ветвям дерева и просуммируем длины пройденных ветвей, результат будет равен расстоянию между этими таксонами во входной матрице расстояний. Например, переходя от $d\; \{\backslash \; displaystyle\; d\}$к $b\; \{\backslash \; displaystyle\; b\}$, мы имеем $2\; +\; 2\; +\; 3\; +\; 3\; =\; 10\; \{\backslash \; Displaystyle\; 2\; +\; 2\; +\; 3\; +\; 3\; =\; 10\}$. Матрица расстояний, расстояния которой совпадают таким образом с некоторым деревом, называется «аддитивной», что редко встречается на практике. Тем не менее, важно отметить, что, учитывая аддитивную матрицу расстояний в качестве входных данных, соединение соседей гарантированно найдет дерево, расстояния между таксонами которого согласуются с ним.

Объединение соседей как минимальная эволюция

Объединение соседей можно рассматривать как жадную эвристику для критерия сбалансированного минимального развития (BME). Для каждой топологии BME определяет длину дерева (сумму длин ветвей) как конкретную взвешенную сумму расстояний в матрице расстояний с весами, зависящими от топологии. Оптимальная топология BME - это та, которая минимизирует длину этого дерева. Присоединение соседей на каждом шаге жадно присоединяется к той паре таксонов, которая дает наибольшее уменьшение предполагаемой длины дерева. Эта процедура не гарантирует нахождения оптимума по критерию BME, хотя часто дает и обычно довольно близка.

Преимущества и недостатки

Основным достоинством NJ является то, что он быстрее по сравнению с наименьшими квадратами, максимальной экономией и максимальной вероятность. Это делает его практичным для анализа больших наборов данных (сотни или тысячи таксонов) и для самонастройки, для чего используются другие средства анализа (например, максимальная экономия, максимальная вероятность ) может быть вычислительно недопустимым.

Объединение соседей имеет свойство, заключающееся в том, что если входная матрица расстояний верна, то выходное дерево будет правильным. Более того, правильность топологии выходного дерева гарантируется, пока матрица расстояний является «почти аддитивной», в частности, если каждая запись в матрице расстояний отличается от истинного расстояния менее чем на половину длины самой короткой ветви в дереве. На практике матрица расстояний редко удовлетворяет этому условию, но объединение соседей часто в любом случае создает правильную топологию дерева. Правильность объединения соседей для почти аддитивных матриц расстояний означает, что оно статистически согласовано во многих моделях эволюции; с учетом данных достаточной длины, соединение соседей с большой вероятностью восстановит истинное дерево. По сравнению с UPGMA и WPGMA объединение соседей имеет то преимущество, что оно не предполагает, что все клоны развиваются с одинаковой скоростью (гипотеза молекулярных часов ).

Тем не менее, объединение соседей в значительной степени вытеснено филогенетическими методами, которые не полагаются на измерение расстояния и обеспечивают превосходную точность в большинстве условий. Соединение по соседству имеет нежелательную особенность, заключающуюся в том, что некоторым ответвлениям часто присваивается отрицательная длина.

Реализации и варианты

Есть много доступных программ, реализующих соединение соседей. RapidNJ и NINJA - это быстрые реализации с типичным временем выполнения, пропорциональным приблизительно квадрату количества таксонов. BIONJ и Weighbor - это варианты объединения соседей, которые улучшают его точность за счет использования того факта, что более короткие расстояния в матрице расстояний обычно лучше известны, чем более длинные расстояния. FastME - это реализация тесно связанного метода сбалансированной минимальной эволюции.

См. Также

• Поиск ближайшего соседа
• UPGMA и WPGMA
• Минимальная эволюция

Ссылки

Другие источники

Внешние links

• Метод соединения соседей - учебное пособие