В теории категорий, разделе математики, изображение морфизма является обобщением изображения функции .
Содержание
- 1 Общее определение
- 2 Второе определение
- 3 Примеры
- 4 См. Также
- 5 Ссылки
Общее определение
Для категории  и a морфизм
и a морфизм  в
в  , изображение из
, изображение из  является мономорфизмом
является мономорфизмом  , удовлетворяющий следующему универсальному свойству :
, удовлетворяющий следующему универсальному свойству :
- Существует морфизм
 такой, что
такой, что  .
. - Для любого объекта
 с морфизмом
с морфизмом  и мономорфизм
и мономорфизм  такой, что
такой, что  , существует уникальный морфизм
, существует уникальный морфизм  такой, что
такой, что  .
.
Примечания:
- такая факторизация не обязательно существует.
 уникален по определению
уникален по определению  monic.
monic. by
by  monic.
monic. является моническим.
является моническим. уже подразумевает, что
уже подразумевает, что  является уникальным.
является уникальным.


Изображение  часто обозначается
часто обозначается  или
или  .
.
Предложение: Если  имеет все эквалайзеры, то
имеет все эквалайзеры, то  в факторизации
в факторизации  of (1) является эпиморфизмом.
of (1) является эпиморфизмом.
Доказательство -
Пусть  таково, что
таково, что  , нужно показать, что
, нужно показать, что  . Поскольку существует эквалайзер
. Поскольку существует эквалайзер  ,
,  разлагается на
разлагается на  с
с  monic. Но тогда
monic. Но тогда  является факторизацией
является факторизацией  с мономорфизмом
с мономорфизмом  . Следовательно, по универсальному свойству изображения существует уникальная стрелка
. Следовательно, по универсальному свойству изображения существует уникальная стрелка  такая, что
такая, что  и поскольку
и поскольку  является моническим
является моническим  . Кроме того, имеется
. Кроме того, имеется  и по свойству мономорфизма
и по свойству мономорфизма  получается
получается  .
.

Это означает что  и, следовательно,
и, следовательно,  выравнивает
выравнивает  , откуда
, откуда  .
.
Второе определение
В категории  со всеми конечными пределами и colimits, изображение изображение определяется как уравнитель
со всеми конечными пределами и colimits, изображение изображение определяется как уравнитель  так называемой пары коядра
так называемой пары коядра  .
.
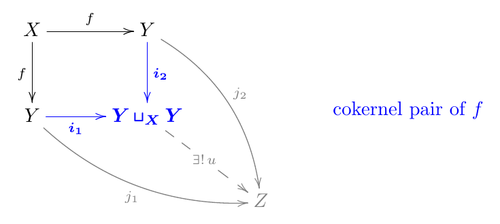

Примечания:
- Конечная биполнота категории гарантирует, что существуют выталкивающие элементы и эквалайзеры.
 можно назвать обычным изображением, поскольку
можно назвать обычным изображением, поскольку  является регулярный мономорфизм, т.е. уравнитель парного морфизма. (Напомним также, что эквалайзер автоматически является мономорфизмом).
является регулярный мономорфизм, т.е. уравнитель парного морфизма. (Напомним также, что эквалайзер автоматически является мономорфизмом).- В абелевой категории свойство пары коядров может быть записано
 и условие эквалайзера
и условие эквалайзера  . Более того, все мономорфизмы регулярны.
. Более того, все мономорфизмы регулярны.
Теорема - Если  всегда факторизуется через регулярные мономорфизмы, то эти два определения совпадают.
всегда факторизуется через регулярные мономорфизмы, то эти два определения совпадают.
Доказательство —
Первое определение подразумевает второе: Предположим, что (1) выполняется с  регулярным мономорфизмом.
регулярным мономорфизмом.
- Выравнивание: нужно показать, что
 . В качестве пары коядров
. В качестве пары коядров  и по предыдущему предложению, поскольку
и по предыдущему предложению, поскольку  имеет все эквалайзеры, стрелка
имеет все эквалайзеры, стрелка  в факторизации
в факторизации  является эпиморфизмом, следовательно,
является эпиморфизмом, следовательно,  .
. - Универсальность: в категории со всеми копределами (или, по крайней мере, со всеми выталкивающими элементами)
 само по себе допускает пару коядров
само по себе допускает пару коядров 

- Более того, как регулярный мономорфизм,
 является уравнителем пары морфизмов
является уравнителем пары морфизмов  , но здесь мы утверждаем, что он также является эквалайзером
, но здесь мы утверждаем, что он также является эквалайзером  .
. - Действительно, по построению
 , таким образом, диаграмма «пары коядров» для
, таким образом, диаграмма «пары коядров» для  дает уникальный морфизм
дает уникальный морфизм  такой, что
такой, что  . Теперь карта
. Теперь карта  , которая уравнивает
, которая уравнивает  также удовлетворяет
также удовлетворяет  , следовательно, схема эквалайзера для
, следовательно, схема эквалайзера для  , существует уникальная карта
, существует уникальная карта  так, что
так, что  .
. - Наконец, используйте диаграмму пары коядров (из
 ) с
) с  : существует уникальный
: существует уникальный  такой, что
такой, что  . Следовательно, любая карта
. Следовательно, любая карта  , которая уравнивает
, которая уравнивает  также выравнивает
также выравнивает  и, таким образом, однозначно разлагается на множители как
и, таким образом, однозначно разлагается на множители как  . Это в точности означает, что
. Это в точности означает, что  является эквалайзером
является эквалайзером  .
.
Второе определение подразумевает первое:
- Факторизация: взятие
 в эквалайзере диаграмма (
в эквалайзере диаграмма ( соответствует
соответствует  ), получаем факторизацию
), получаем факторизацию  .
. - Универсальность: пусть
 будет факторизацией с
будет факторизацией с  регулярный мономорфизм, то есть эквалайзер некоторой пары
регулярный мономорфизм, то есть эквалайзер некоторой пары  .
.
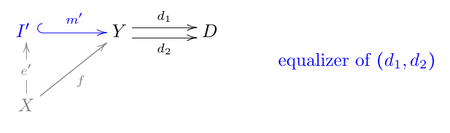
- Тогда
 так, чтобы по диаграмме «пара коядров» (из
так, чтобы по диаграмме «пара коядров» (из  ), с
), с  , существует уникальный
, существует уникальный  так, что
так, что  .
. - Теперь из
 (m из эквалайзера диаграммы (i 1, i 2)), получаем
(m из эквалайзера диаграммы (i 1, i 2)), получаем  , следовательно, в силу универсальности (эквалайзера (d 1, d 2) с заменой f на m) существует уникальная диаграмма
, следовательно, в силу универсальности (эквалайзера (d 1, d 2) с заменой f на m) существует уникальная диаграмма  такая, что
такая, что  .
.
Примеры
В категории наборов изображение морфизма  - это включение из обычного изображения
- это включение из обычного изображения  до
до  . Во многих конкретных категориях, таких как группы, абелевы группы и (левые или правые) модули, образ морфизма является образ соответствующего морфизма в категории множеств.
. Во многих конкретных категориях, таких как группы, абелевы группы и (левые или правые) модули, образ морфизма является образ соответствующего морфизма в категории множеств.
В любой нормальной категории с нулевым объектом и ядрами и коядрами для каждого морфизма изображение морфизм  можно выразить следующим образом:
можно выразить следующим образом:
- im f = ker coker f
В абелевой категории (которая, в частности, является бинормальной), если f - мономорфизм, то f = ker coker f, поэтому f = im f.
См. Также
Ссылки





 такой, что
такой, что  .
. с морфизмом
с морфизмом  и мономорфизм
и мономорфизм  такой, что
такой, что  , существует уникальный морфизм
, существует уникальный морфизм  такой, что
такой, что  .
. уникален по определению
уникален по определению  monic.
monic. by
by  monic.
monic. является моническим.
является моническим. уже подразумевает, что
уже подразумевает, что  является уникальным.
является уникальным.

































 можно назвать обычным изображением, поскольку
можно назвать обычным изображением, поскольку  является регулярный мономорфизм, т.е. уравнитель парного морфизма. (Напомним также, что эквалайзер автоматически является мономорфизмом).
является регулярный мономорфизм, т.е. уравнитель парного морфизма. (Напомним также, что эквалайзер автоматически является мономорфизмом). и условие эквалайзера
и условие эквалайзера  . Более того, все мономорфизмы регулярны.
. Более того, все мономорфизмы регулярны.

 . В качестве пары коядров
. В качестве пары коядров  и по предыдущему предложению, поскольку
и по предыдущему предложению, поскольку  имеет все эквалайзеры, стрелка
имеет все эквалайзеры, стрелка  в факторизации
в факторизации  является эпиморфизмом, следовательно,
является эпиморфизмом, следовательно,  .
. само по себе допускает пару коядров
само по себе допускает пару коядров 

 является уравнителем пары морфизмов
является уравнителем пары морфизмов  , но здесь мы утверждаем, что он также является эквалайзером
, но здесь мы утверждаем, что он также является эквалайзером  .
. , таким образом, диаграмма «пары коядров» для
, таким образом, диаграмма «пары коядров» для  дает уникальный морфизм
дает уникальный морфизм  такой, что
такой, что  . Теперь карта
. Теперь карта  , которая уравнивает
, которая уравнивает  также удовлетворяет
также удовлетворяет  , следовательно, схема эквалайзера для
, следовательно, схема эквалайзера для  , существует уникальная карта
, существует уникальная карта  так, что
так, что  .
. ) с
) с  : существует уникальный
: существует уникальный  такой, что
такой, что  . Следовательно, любая карта
. Следовательно, любая карта  , которая уравнивает
, которая уравнивает  также выравнивает
также выравнивает  и, таким образом, однозначно разлагается на множители как
и, таким образом, однозначно разлагается на множители как  . Это в точности означает, что
. Это в точности означает, что  является эквалайзером
является эквалайзером  .
. в эквалайзере диаграмма (
в эквалайзере диаграмма ( соответствует
соответствует  ), получаем факторизацию
), получаем факторизацию  .
. будет факторизацией с
будет факторизацией с  регулярный мономорфизм, то есть эквалайзер некоторой пары
регулярный мономорфизм, то есть эквалайзер некоторой пары  .
.
 так, чтобы по диаграмме «пара коядров» (из
так, чтобы по диаграмме «пара коядров» (из  ), с
), с  , существует уникальный
, существует уникальный  так, что
так, что  .
. (m из эквалайзера диаграммы (i 1, i 2)), получаем
(m из эквалайзера диаграммы (i 1, i 2)), получаем  , следовательно, в силу универсальности (эквалайзера (d 1, d 2) с заменой f на m) существует уникальная диаграмма
, следовательно, в силу универсальности (эквалайзера (d 1, d 2) с заменой f на m) существует уникальная диаграмма  такая, что
такая, что  .
.


