График дружбы

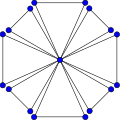График дружбы
Граф дружбы F 8.
Вершины	2n + 1
Края	3n
Радиус	1
Диаметр	2
Обхват	3
Хроматическое число	3
Хроматический индекс	2n
Характеристики
Обозначение	F n
Таблица графиков и параметров

В математической области теории графов, то дружба граф (или Голландская мельница графики или п -веерный) Р п является плоской неориентированным граф с 2n + 1 вершины и 3n ребер.

Граф дружбы F n может быть построен путем соединения n копий графа циклов C 3 с общей вершиной.

По построению граф дружбы F n изоморфен графу ветряных мельниц Wd (3, n). Это единичное расстояние с обхватом 3, диаметром 2 и радиусом 1. График F 2 изоморфен графику бабочки.

• 1 Теорема о дружбе
• 2 Маркировка и окраска
• 3 Экстремальная теория графов
• 4 ссылки

Теорема дружбы из Эрдёша, Рения, и Вера Т. Сос  ( 1966) утверждает, что конечные графы с тем свойством, что каждые две вершин имеют ровно один сосед обычны именно дружба графика. Неформально, если группа людей обладает свойством, заключающимся в том, что у каждой пары людей есть ровно один общий друг, тогда должен быть один человек, который является другом для всех остальных. Однако для бесконечных графов может быть много разных графов с одинаковой мощностью, которые обладают этим свойством.

Комбинаторное доказательство теоремы о дружбе было дано Мерциосом и Унгером. Еще одно доказательство предоставил Крейг Хунеке. Формализованное доказательство в Metamath было опубликовано Александром ван дер Векенсом в октябре 2018 года в списке рассылки Metamath.

Граф дружбы имеет хроматическое число 3 и хроматический индекс 2n. Его хроматический полином может быть выведен из хроматического полинома графа циклов C 3 и равен. ${\ Displaystyle (х-2) ^ {п} (х-1) ^ {п} х}$

Дружба граф Г п является ребром изящного тогда и только тогда, когда п нечетно. Это изящно тогда и только тогда, когда n ≡ 0 (mod 4) или n ≡ 1 (mod 4).

Каждый граф дружбы имеет решающее значение.

Согласно теории экстремальных графов, каждый граф с достаточно большим числом ребер (относительно числа его вершин) должен содержать -вентилятор в качестве подграфа. В частности, это верно для -вершинного графа, если количество ребер равно ${\ displaystyle k}$${\ displaystyle n}$

${\ displaystyle \ left \ lfloor {\ frac {n ^ {2}} {4}} \ right \ rfloor + f (k),}$

где есть если нечетное, а есть если четное. Эти оценки обобщают теорему Турана о количестве ребер в графе без треугольников, и они являются наилучшими возможными оценками для этой проблемы, поскольку для любого меньшего числа ребер существуют графы, не содержащие -вернутый. ${\ displaystyle f (k)}$${\ displaystyle k ^ {2} -k}$${\ displaystyle k}$${\ displaystyle f (k)}$${\ displaystyle k ^ {2} -3k / 2}$${\ displaystyle k}$ ${\ displaystyle k}$