Все неизоморфные графы с 3 вершинами и их хроматические многочлены, по часовой стрелке сверху. Независимый 3-набор:

. Ребро и одна вершина:

. 3-путь:

. 3-клика:

.
Хроматический полином - это многочлен графов изучается в алгебраической теории графов, разделе математики. Он подсчитывает количество раскрасок графика как функцию количества цветов и был первоначально определен Джорджем Дэвидом Биркгофом для изучения четырехцветной проблемы. Он был обобщен на многочлен Тутте Хасслером Уитни и У. Т. Тутт, связав его с моделью Поттса из статистической физики.
Содержание
- 1 История
- 2 Определение
- 2.1 Удаление – сокращение
- 3 Примеры
- 4 Свойства
- 4.1 Хроматическая эквивалентность
- 4.2 Хроматические корни
- 4.3 Раскраска с использованием всех цветов
- 4.4 Категоризация
- 5 Алгоритмы
- 5.1 Эффективные алгоритмы
- 5.2 Удаление – сжатие
- 5.3 Метод куба
- 5.4 Вычислительная сложность
- 6 Примечания
- 7 Ссылки
- 8 Внешние ссылки
История
Джордж Дэвид Биркгоф представил хроматический полином в 1912 году, определив его только для плоских графов, в попытке доказать теорему о четырех цветах. Если  обозначает количество правильных раскрасок G с помощью k цветов, то можно установить теорему о четырех цветах, показав
обозначает количество правильных раскрасок G с помощью k цветов, то можно установить теорему о четырех цветах, показав  для всех плоских графов G. Таким образом он надеялся применить мощные инструменты анализа и алгебры для изучения корней многочленов в проблеме комбинаторной раскраски.
для всех плоских графов G. Таким образом он надеялся применить мощные инструменты анализа и алгебры для изучения корней многочленов в проблеме комбинаторной раскраски.
Хасслер Уитни обобщил полином Биркгофа с плоского случая на общие графы в 1932 году. В 1968 году Рид спросил, какие многочлены являются хроматическими многочленами некоторого графа, вопрос, который остается открытым, и ввел концепция хроматически эквивалентных графов. Сегодня хроматические многочлены являются одним из центральных объектов теории алгебраических графов.
Определение

Все правильные раскраски вершин вершинных графов с 3 вершины с использованием k цветов для

. Хроматический многочлен каждого графа интерполируется по количеству правильных раскрасок.
Для графа G  подсчитывает число его (собственных) вершинных k-раскрасок. Другие часто используемые обозначения включают
подсчитывает число его (собственных) вершинных k-раскрасок. Другие часто используемые обозначения включают  ,
,  , или
, или  . Существует уникальный полином
. Существует уникальный полином  , который вычисляется для любого целого числа k ≥ 0 и совпадает с
, который вычисляется для любого целого числа k ≥ 0 и совпадает с  ; он называется хроматическим многочленом от G.
; он называется хроматическим многочленом от G.
Например, чтобы раскрасить граф путей  на 3 вершинах с k цветов, можно выбрать любой из k цветов для первой вершины, любой из
на 3 вершинах с k цветов, можно выбрать любой из k цветов для первой вершины, любой из  оставшихся цветов для вторая вершина и, наконец, для третьей вершины любой из цветов
оставшихся цветов для вторая вершина и, наконец, для третьей вершины любой из цветов  , которые отличаются от цветов, выбранных второй вершиной. Следовательно,
, которые отличаются от цветов, выбранных второй вершиной. Следовательно,  - количество k-раскрасок
- количество k-раскрасок  . Для переменной x (не обязательно целого числа), таким образом,
. Для переменной x (не обязательно целого числа), таким образом,  . (Раскраски, которые различаются только перестановкой цветов или автоморфизмами группы G, по-прежнему считаются разными.)
. (Раскраски, которые различаются только перестановкой цветов или автоморфизмами группы G, по-прежнему считаются разными.)
Удаление – сжатие
Тот факт, что количество k-раскрасок является многочленом от k, что следует из рекуррентного соотношения, называемого повторением удаления-сокращения или Фундаментальной теоремой сведения . Он основан на сжатии ребер : для пары вершин  и
и  Граф
Граф  получается путем слияния двух вершин и удаления всех ребер между ними. Если
получается путем слияния двух вершин и удаления всех ребер между ними. Если  и
и  смежны в G, пусть
смежны в G, пусть  обозначает граф, полученный удалением ребра
обозначает граф, полученный удалением ребра  . Тогда количество k-раскрасок этих графов удовлетворяет:
. Тогда количество k-раскрасок этих графов удовлетворяет:

Эквивалентно, если  и
и  не являются смежными в G и
не являются смежными в G и  - это граф с ребром
- это граф с ребром  добавлено, тогда
добавлено, тогда

Это следует из наблюдения, что каждая k-раскраска G дает разные цвета для  и
и  или тех же цветов. В первом случае это дает (правильную) k-раскраску
или тех же цветов. В первом случае это дает (правильную) k-раскраску  , а во втором случае - раскраску
, а во втором случае - раскраску  . И наоборот, каждую k-раскраску G можно однозначно получить из k-раскраски
. И наоборот, каждую k-раскраску G можно однозначно получить из k-раскраски  или
или  (если
(если  и
и  не являются смежными в G).
не являются смежными в G).
Следовательно, хроматический полином может быть рекурсивно определен как
 для граф без ребер на n вершинах и
для граф без ребер на n вершинах и для графа G с ребром
для графа G с ребром  (произвольно выбранный).
(произвольно выбранный).
Поскольку количество k-раскрасок графа без ребер действительно равно  , по индукции по количеству ребер следует, что для всех G многочлен
, по индукции по количеству ребер следует, что для всех G многочлен  совпадает с количеством k-раскрасок в каждой целой точке x = k. В частности, хроматический многочлен - это единственный интерполирующий многочлен степени не выше n через точки
совпадает с количеством k-раскрасок в каждой целой точке x = k. В частности, хроматический многочлен - это единственный интерполирующий многочлен степени не выше n через точки

Любопытство Тютта о том, какие другие графовые инварианты удовлетворяют таким повторениям, привело его к открытию двумерного обобщения хроматического полинома, полинома Тутте  .
.
Примеры
Хроматические многочлены для некоторых графовТреугольник  |  |
Полный график  |  |
граф без ребер  |  |
График пути  |  |
| Любое дерево на n вершинах |  |
Цикл  |  |
| график Петерсена |  |
Свойства
Для фиксированный G на n вершинах, хроматический многочлен  является monic многочленом степени ровно n, с целочисленные коэффициенты.
является monic многочленом степени ровно n, с целочисленные коэффициенты.
Хроматический полином включает, по меньшей мере, столько же информации о возможности окраски G, сколько и хроматическое число. Действительно, хроматическое число - это наименьшее натуральное число, не являющееся нулем хроматического многочлена,

Полином оценен как <\235>- 1 displaystyle -1} , то есть
, то есть  , дает
, дает  , умноженное на количество ациклических ориентаций G.
, умноженное на количество ациклических ориентаций G.
производная, вычисленная как 1,  равняется
равняется  до знака.
до знака.
Если G имеет n вершин и c компонентов  , затем
, затем
- Коэффициенты
 - нули.
- нули. - Коэффициенты
 все ненулевые и чередуются в знаках.
все ненулевые и чередуются в знаках. - Коэффициент
 равен 1 (многочлен monic ).
равен 1 (многочлен monic ). - Коэффициент
 равно
равно  .
.
Доказательство- Просмотр, щелкнув [показать] - Мы докажем это индукцией по количеству ребер на простом графе G с

вершин и

ребер. Когда

, G - пустой график. Следовательно, согласно определению

. Таким образом, коэффициент при

равен

, что означает, что утверждение верно для пустого графа. Когда

, как в G имеет только одно ребро,

. Таким образом, коэффициент

равен

. Таким образом, утверждение верно для k = 1. Используя
сильную индукцию, предположим, что утверждение верно для

. Пусть G имеет

ребер. По принципу
сокращения-удаления,
 ,
,
Пусть

и

.. Следовательно,

.. Поскольку

получается из G удалением только одного ребра e,

, поэтому

и, таким образом, утверждение верно для k.
- Коэффициент при
 равен
равен  , умноженное на количество ациклических ориентаций, которые имеют уникальный сток, в указанной произвольно выбранной вершине.
, умноженное на количество ациклических ориентаций, которые имеют уникальный сток, в указанной произвольно выбранной вершине. - Абсолютные значения коэффициентов каждого хроматического полинома образуют логарифмически вогнутую форму. последовательность.

Последнее свойство обобщается тем, что если G является k-кликовой суммой из  и
и  (т. Е. График, полученный склейкой два в клике на k вершинах), то
(т. Е. График, полученный склейкой два в клике на k вершинах), то

Граф G с n вершинами является деревом тогда и только тогда, когда

Хроматическая эквивалентность
 Три графика с хроматическим полиномом, равным
Три графика с хроматическим полиномом, равным  .
.Два графа называются хроматически эквивалентными, если они имеют один и тот же хроматический многочлен. Изоморфные графы имеют один и тот же хроматический полином, но неизоморфные графы могут быть хроматически эквивалентными. Например, все деревья на n вершинах имеют один и тот же хроматический полином. В частности,  является хроматическим многочленом как для графа когтей, так и для граф путей на 4 вершинах.
является хроматическим многочленом как для графа когтей, так и для граф путей на 4 вершинах.
Граф хроматически уникален, если он определяется своим хроматическим полиномом с точностью до изоморфизма. Другими словами, G хроматически уникален, тогда  будет следует, что G и H изоморфны. Все графы цикла хроматически уникальны.
будет следует, что G и H изоморфны. Все графы цикла хроматически уникальны.
Хроматические корни
A корень (или ноль) хроматического многочлена, называемого «хроматическим корнем», - это значение x, где  . Хроматические корни были очень хорошо изучены. Фактически, первоначальная мотивация Биркгофа для определения хроматического полинома заключалась в том, чтобы показать, что для плоских графов
. Хроматические корни были очень хорошо изучены. Фактически, первоначальная мотивация Биркгофа для определения хроматического полинома заключалась в том, чтобы показать, что для плоских графов  для x ≥ 4. Это установило бы теорему о четырех цветах.
для x ≥ 4. Это установило бы теорему о четырех цветах.
Ни один граф не может быть 0-цветным, поэтому 0 всегда является хроматическим корнем. граф с хотя бы одним ребром. С другой стороны, за исключением этих двух точек, ни один граф не может иметь хроматический корень с действительным числом, меньшим или равным 32/27. Результат Тутте соединяет золотое сечение  с изучением хроматических корней, показывающим, что хроматические корни существуют очень близко к
с изучением хроматических корней, показывающим, что хроматические корни существуют очень близко к  : если
: если  является pl при арной триангуляции сферы
является pl при арной триангуляции сферы

В то время как вещественная линия, таким образом, имеет большие части, не содержащие хроматических корней для любого графа, каждый точка на комплексной плоскости произвольно близка к хроматическому корню в том смысле, что существует бесконечное семейство графов, хроматические корни которых плотны в комплексной плоскости.
Раскраски с использованием всех цветов
Для графа G на n вершинах, пусть  обозначает количество раскрасок с использованием ровно k цветов с точностью до переименования цветов (чтобы цвета, которые могли быть полученными друг от друга перестановкой цветов, считаются как один; раскраски, полученные с помощью автоморфизмов группы G, по-прежнему считаются отдельно). Другими словами,
обозначает количество раскрасок с использованием ровно k цветов с точностью до переименования цветов (чтобы цвета, которые могли быть полученными друг от друга перестановкой цветов, считаются как один; раскраски, полученные с помощью автоморфизмов группы G, по-прежнему считаются отдельно). Другими словами,  подсчитывает количество разделов набора вершин на k (непустых) независимых наборов. Тогда
подсчитывает количество разделов набора вершин на k (непустых) независимых наборов. Тогда  подсчитывает количество раскрасок, используя ровно k цветов (с различимыми цветами). Для целого числа x все x-раскраски G могут быть однозначно получены путем выбора целого числа k ≤ x, выбора k цветов из имеющихся x и раскраски с использованием именно этих k (различимых) цветов. Следовательно:
подсчитывает количество раскрасок, используя ровно k цветов (с различимыми цветами). Для целого числа x все x-раскраски G могут быть однозначно получены путем выбора целого числа k ≤ x, выбора k цветов из имеющихся x и раскраски с использованием именно этих k (различимых) цветов. Следовательно:
 ,
,
где  обозначает факториал падения. Таким образом, числа
обозначает факториал падения. Таким образом, числа  являются коэффициентами многочлена
являются коэффициентами многочлена  в основании
в основании  падающих факториалов.
падающих факториалов.
Пусть  будет k-м коэффициентом
будет k-м коэффициентом  в стандартном базисе
в стандартном базисе  , то есть:
, то есть:

Числа Стирлинга дают изменение базиса между стандартным базисом и базисом падающих факториалов. Это означает:
 и
и  .
.
Категоризация
Хроматический полином категоризован теорией гомологии, тесно связанной с гомологией Хованова.
Алгоритмы
| Хроматический многочлен |
|---|
| Входные данные | График G с n вершинами. |
|---|
| Выходные данные | Коэффициенты  |
|---|
| Время выполнения |  для некоторой константы для некоторой константы  |
|---|
| Сложность | #P -hard |
|---|
| Уменьшение с | # 3SAT |
|---|
| # k- раскраски |
|---|
| Входные | График G с n вершинами. |
|---|
| Выходные |  |
|---|
| Время работы | В P для  . .  для для  . В противном случае . В противном случае  для некоторой константы для некоторой константы  |
|---|
| Сложность | #P -hard, если  |
|---|
| Approximability | Нет FPRAS для  |
|---|
Вычислительные проблемы, связанные с хроматическим полиномом, включают
- поиск хроматического полинома
 заданного графа G;
заданного графа G; - оценка
 в фиксированной точке x для данного G.
в фиксированной точке x для данного G.
Первая проблема более общая, потому что если мы знали коэффициенты  , мы могли оценить его в любой момент полиномиального времени, потому что степень равна n. Сложность второй тип задач сильно зависит от значения x и имеет n интенсивно изучается в вычислительной сложности. Когда x - натуральное число, эта задача обычно рассматривается как вычисление количества раскрасок по x данного графа. Например, сюда входит задача # 3-раскраска подсчета количества 3-раскрасок, каноническая проблема в изучении сложности подсчета, полная для класса подсчета #P.
, мы могли оценить его в любой момент полиномиального времени, потому что степень равна n. Сложность второй тип задач сильно зависит от значения x и имеет n интенсивно изучается в вычислительной сложности. Когда x - натуральное число, эта задача обычно рассматривается как вычисление количества раскрасок по x данного графа. Например, сюда входит задача # 3-раскраска подсчета количества 3-раскрасок, каноническая проблема в изучении сложности подсчета, полная для класса подсчета #P.
Эффективные алгоритмы
Для некоторых базовых классов графов известны замкнутые формулы хроматического полинома. Например, это верно для деревьев и клик, перечисленных в таблице выше.
Известны алгоритмы полиномиального времени для вычисления хроматического полинома для более широких классов графов, включая хордовые графы и графы с ограниченной шириной клики . Последний класс включает кографы и графы с ограниченной древовидной шириной, такие как внешнепланарные графы.
Удаление – сжатие
Удаление - Повторение сокращения дает способ вычисления хроматического полинома, называемого алгоритмом удаления-сокращения. В первой форме (с минусом) повторение заканчивается набором пустых графов. Во второй форме (с плюсом) он завершается набором полных графиков. Это составляет основу многих алгоритмов раскраски графов. Функция ChromaticPolynomial в пакете Combinatorica системы компьютерной алгебры Mathematica использует второе повторение, если график плотный, и первое повторение, если график разреженный. Время выполнения любой формулы в наихудшем случае удовлетворяет тому же рекуррентному соотношению, что и числа Фибоначчи, поэтому в худшем случае алгоритм выполняется во времени с полиномиальным множителем

на графе с n вершинами и m ребрами. Анализ может быть улучшен с точностью до полиномиального множителя числа  из остовных деревьев входного графа. На практике, чтобы избежать некоторых рекурсивных вызовов, используются стратегии ветвей и границ и отказ от изоморфизма графов, время выполнения зависит от эвристики, используемой для выбора пары вершин.
из остовных деревьев входного графа. На практике, чтобы избежать некоторых рекурсивных вызовов, используются стратегии ветвей и границ и отказ от изоморфизма графов, время выполнения зависит от эвристики, используемой для выбора пары вершин.
Метод куба
Существует естественная геометрическая перспектива раскраски графа, если заметить, что при присвоении натуральных чисел каждой вершине раскраска графа является вектором в целочисленной решетке. Поскольку двум вершинам  и
и  задан один и тот же цвет, это эквивалентно
задан один и тот же цвет, это эквивалентно  '-я и
'-я и  ' -я координаты в векторе раскраски равны, каждое ребро может быть связано с гиперплоскостью вида
' -я координаты в векторе раскраски равны, каждое ребро может быть связано с гиперплоскостью вида  . Набор таких гиперплоскостей для данного графа называется его графическим расположением. Правильная раскраска графа - это те точки решетки, которые избегают запрещенных гиперплоскостей. Ограничивая набором цветов
. Набор таких гиперплоскостей для данного графа называется его графическим расположением. Правильная раскраска графа - это те точки решетки, которые избегают запрещенных гиперплоскостей. Ограничивая набором цветов  , точки решетки содержатся в кубе
, точки решетки содержатся в кубе ![[ 0, k] ^ {n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8df6fe0f0693f5c9e7c12c2cb0e2631660d37344) . В этом контексте хроматический полином подсчитывает количество точек решетки в
. В этом контексте хроматический полином подсчитывает количество точек решетки в ![[0, k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dda1392a37e0feafb1454ceec449724ab056a3a) -куб, которые избегают графического расположения.
-куб, которые избегают графического расположения.
Вычислительная сложность
Задача вычисления количества трехцветных раскрасок данного графа является каноническим примером #P -полной задачи, поэтому проблема вычисление коэффициентов хроматического полинома является # P-трудным. Аналогичным образом, оценка  для данного G является # P-завершенной. С другой стороны, для
для данного G является # P-завершенной. С другой стороны, для  легко вычислить
легко вычислить  , поэтому соответствующие задачи вычислимы за полиномиальное время. Для целых чисел
, поэтому соответствующие задачи вычислимы за полиномиальное время. Для целых чисел  проблема заключается в # P-hard, который устанавливается аналогично случаю
проблема заключается в # P-hard, который устанавливается аналогично случаю  . Фактически, известно, что
. Фактически, известно, что  является # P-сложным для всех x (включая отрицательные целые и даже все комплексные числа), кроме три «легких точки». Таким образом, с точки зрения жесткости # P, сложность вычисления хроматического полинома полностью понятна.
является # P-сложным для всех x (включая отрицательные целые и даже все комплексные числа), кроме три «легких точки». Таким образом, с точки зрения жесткости # P, сложность вычисления хроматического полинома полностью понятна.
В разложении

коэффициент  всегда равен 1, и некоторые другие свойства коэффициентов известны. Это вызывает вопрос, являются ли некоторые из коэффициентов легко вычислить. Однако вычисление Вся проблема вычисления a r для фиксированного r ≥ 1 и данного графа G является # P-сложной даже для двудольных плоских графов.
всегда равен 1, и некоторые другие свойства коэффициентов известны. Это вызывает вопрос, являются ли некоторые из коэффициентов легко вычислить. Однако вычисление Вся проблема вычисления a r для фиксированного r ≥ 1 и данного графа G является # P-сложной даже для двудольных плоских графов.
Нет алгоритмов аппроксимации для вычисления  известны для любого x, кроме трех простых точек. В целочисленных точках
известны для любого x, кроме трех простых точек. В целочисленных точках  соответствующая задача принятия решения о том, может ли данный граф быть k-цветным - это NP-hard. Такие задачи не могут быть приближены к любому мультипликативному коэффициенту вероятностным алгоритмом с ограниченной ошибкой, если NP = RP, потому что любое мультипликативное приближение будет различать значения 0 и 1, эффективно решая версию решения за вероятностное полиномиальное время с ограниченной ошибкой. В частности, при том же предположении это исключает возможность полностью полиномиальной схемы рандомизированной аппроксимации (FPRAS). По другим пунктам нужны более сложные аргументы, и этот вопрос находится в центре активных исследований. По состоянию на 2008 год известно, что не существует FPRAS для вычисления
соответствующая задача принятия решения о том, может ли данный граф быть k-цветным - это NP-hard. Такие задачи не могут быть приближены к любому мультипликативному коэффициенту вероятностным алгоритмом с ограниченной ошибкой, если NP = RP, потому что любое мультипликативное приближение будет различать значения 0 и 1, эффективно решая версию решения за вероятностное полиномиальное время с ограниченной ошибкой. В частности, при том же предположении это исключает возможность полностью полиномиальной схемы рандомизированной аппроксимации (FPRAS). По другим пунктам нужны более сложные аргументы, и этот вопрос находится в центре активных исследований. По состоянию на 2008 год известно, что не существует FPRAS для вычисления  для любого x>2, кроме случаев, когда NP = RP держит.
для любого x>2, кроме случаев, когда NP = RP держит.
Примечания
Ссылки
Внешние ссылки
- Вайсштейн, Эрик У. «Хроматический многочлен». MathWorld.
- PlanetMath Хроматический полином
- Код для вычисления Тутте, Хроматического полинома и полинома потока Гэри Хаггарда, Дэвида Дж. Пирса и Гордона Ройла: [1]
 Все неизоморфные графы с 3 вершинами и их хроматические многочлены, по часовой стрелке сверху. Независимый 3-набор:
Все неизоморфные графы с 3 вершинами и их хроматические многочлены, по часовой стрелке сверху. Независимый 3-набор:  . Ребро и одна вершина:
. Ребро и одна вершина:  . 3-путь:
. 3-путь:  . 3-клика:
. 3-клика:  .
.
для всех плоских графов G. Таким образом он надеялся применить мощные инструменты анализа и алгебры для изучения корней многочленов в проблеме комбинаторной раскраски.
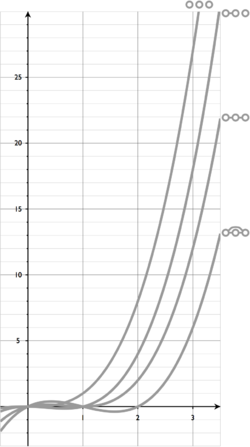
 Все правильные раскраски вершин вершинных графов с 3 вершины с использованием k цветов для
Все правильные раскраски вершин вершинных графов с 3 вершины с использованием k цветов для  . Хроматический многочлен каждого графа интерполируется по количеству правильных раскрасок.
. Хроматический многочлен каждого графа интерполируется по количеству правильных раскрасок. 
































 для граф без ребер на n вершинах и
для граф без ребер на n вершинах и для графа G с ребром
для графа G с ребром  (произвольно выбранный).
(произвольно выбранный).























 - нули.
- нули. все ненулевые и чередуются в знаках.
все ненулевые и чередуются в знаках. равен 1 (многочлен monic ).
равен 1 (многочлен monic ). равно
равно  .
. вершин и
вершин и  ребер. Когда
ребер. Когда  , G - пустой график. Следовательно, согласно определению
, G - пустой график. Следовательно, согласно определению  . Таким образом, коэффициент при
. Таким образом, коэффициент при  равен
равен  , что означает, что утверждение верно для пустого графа. Когда
, что означает, что утверждение верно для пустого графа. Когда  , как в G имеет только одно ребро,
, как в G имеет только одно ребро,  . Таким образом, коэффициент
. Таким образом, коэффициент  равен
равен  . Таким образом, утверждение верно для k = 1. Используя сильную индукцию, предположим, что утверждение верно для
. Таким образом, утверждение верно для k = 1. Используя сильную индукцию, предположим, что утверждение верно для  . Пусть G имеет
. Пусть G имеет  ребер. По принципу сокращения-удаления,
ребер. По принципу сокращения-удаления, 
 и
и  .. Следовательно,
.. Следовательно,  .. Поскольку
.. Поскольку  получается из G удалением только одного ребра e,
получается из G удалением только одного ребра e,  , поэтому
, поэтому  и, таким образом, утверждение верно для k.
и, таким образом, утверждение верно для k.  равен
равен  , умноженное на количество ациклических ориентаций, которые имеют уникальный сток, в указанной произвольно выбранной вершине.
, умноженное на количество ациклических ориентаций, которые имеют уникальный сток, в указанной произвольно выбранной вершине.





 .
.










 ,
,







 и
и  .
.
 для некоторой константы
для некоторой константы 

 .
.  для
для  . В противном случае
. В противном случае  для некоторой константы
для некоторой константы 


 заданного графа G;
заданного графа G; в фиксированной точке x для данного G.
в фиксированной точке x для данного G.








![[ 0, k] ^ {n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8df6fe0f0693f5c9e7c12c2cb0e2631660d37344)
![[0, k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dda1392a37e0feafb1454ceec449724ab056a3a)



проблема заключается в # P-hard, который устанавливается аналогично случаю






