Порог ошибки (эволюция)

редактировать

Ограничение на количество пар оснований, которое может иметь самовоспроизводящаяся молекула, прежде чем мутация уничтожит информацию в последующих поколениях молекулы

В эволюционной биологии и популяционной генетике порог ошибки (или критическая частота мутаций ) составляет ограничение на количество пар оснований, которое может иметь самовоспроизводящаяся молекула до того, как мутация разрушит информацию в последующих поколениях молекулы. Порог ошибки имеет решающее значение для понимания «парадокса Эйгена».

Порог ошибки - это концепция происхождения жизни (абиогенез ), в частности очень ранней жизни, до появления ДНК. Предполагается, что первыми самовоспроизводящимися молекулами могли быть небольшие рибозимные -подобные молекулы РНК. Эти молекулы состоят из цепочек пар оснований или «цифр», и их порядок представляет собой код, который определяет, как молекула взаимодействует с окружающей средой. Всякая репликация подвержена ошибкам мутации. Во время процесса репликации каждая цифра имеет определенную вероятность быть замененной какой-либо другой цифрой, которая изменяет способ взаимодействия молекулы с окружающей средой и может увеличивать или уменьшать ее приспособленность или способность к воспроизводству в этой среде.

Содержание

1 Фитнес-ландшафт
2 Парадокс Эйгена
3 Простая математическая модель
4 См. Также
5 Ссылки

Фитнес-ландшафт

Это было отмечено Манфред Эйген в своей статье 1971 года (Eigen 1971), что этот процесс мутации накладывает ограничение на количество цифр, которые может иметь молекула. Если молекула превышает этот критический размер, эффект мутаций становится подавляющим, и процесс неконтролируемой мутации уничтожает информацию в последующих поколениях молекулы. Порог ошибки также контролируется «ландшафтом пригодности» молекул. Пейзаж фитнеса характеризуется двумя понятиями: рост (= фитнес) и расстояние (= количество мутаций). Подобные молекулы «близки» друг к другу, а молекулы, которые более приспособлены, чем другие, и с большей вероятностью воспроизводятся, «выше» в ландшафте.

Если конкретная последовательность и ее соседи имеют высокую пригодность, они будут формировать квазивиды и смогут поддерживать более длинные последовательности, чем подходящая последовательность с несколькими подходящими соседями или менее подходят окрестности последовательностей. Кроме того, Уилке (Wilke 2005) отмечал, что концепция порога ошибки не применима в тех частях ландшафта, где есть летальные мутации, в которых индуцированная мутация дает нулевую пригодность и запрещает молекулу воспроизводиться.

Парадокс Эйгена

Парадокс Эйгена - одна из самых сложных загадок в изучении происхождения жизни. Считается, что описанная выше концепция порога ошибки ограничивает размер самовоспроизводящихся молекул, возможно, несколькими сотнями цифр, однако почти вся жизнь на Земле требует гораздо более длинных молекул для кодирования своей генетической информации. В живых клетках эта проблема решается ферментами, которые восстанавливают мутации, позволяя кодирующим молекулам достигать размеров порядка миллионов пар оснований. Эти большие молекулы должны, конечно, кодировать те самые ферменты, которые их восстанавливают, и в этом заключается парадокс Эйгена, впервые выдвинутый Манфредом Эйгеном в его статье 1971 года (Eigen 1971). Проще говоря, парадокс Эйгена сводится к следующему:

Без ферментов коррекции ошибок максимальный размер реплицирующейся молекулы составляет около 100 пар оснований.
Чтобы реплицирующаяся молекула кодировала ферменты коррекции ошибок, она должна быть существенно больше 100 оснований.

Это парадокс типа курица или яйцо с еще более трудным решением. Что было первым, большой геном или ферменты для исправления ошибок? Было предложено несколько решений этого парадокса:

Модель стохастического корректора (Szathmáry Maynard Smith, 1995). В этом предложенном решении ряд примитивных молекул, скажем, двух разных типов, каким-то образом связаны друг с другом, возможно, посредством капсулы или «клеточной стенки». Если их репродуктивный успех усиливается за счет, скажем, равного количества в каждой клетке, а воспроизводство происходит путем деления, при котором каждый из различных типов молекул случайным образом распределяется среди «детей», процесс отбора будет способствовать такому равному представлению в клетке. клеток, даже если одна из молекул может иметь селективное преимущество перед другой.
Слабый порог ошибки (Kun et al., 2005) - Исследования реальных рибозимов показывают, что частота мутаций может быть существенно меньше, чем первая. ожидаемый - порядка 0,001 на пару оснований на репликацию. Это может обеспечить длину последовательности порядка 7-8 тысяч пар оснований, что достаточно для включения элементарных ферментов коррекции ошибок.

Простая математическая модель

Рассмотрим молекулу из 3 цифр [A, B, C] где A, B и C могут принимать значения 0 и 1. Таких последовательностей восемь ([000], [001], [010], [011], [100], [101], [110], и [111]). Допустим, молекула [000] является наиболее подходящей; при каждой репликации он производит в среднем $a {\ displaystyle a}$ $a$ копий, где $a>1 {\ displaystyle a>1}$ $a>1$ . Эта молекула называется" главной последовательностью ". семь последовательностей менее подходят; каждая из них дает только одну копию на репликацию. Репликация каждой из трех цифр выполняется со скоростью мутации μ. Другими словами, при каждой репликации цифры последовательности существует вероятность $μ {\ displaystyle \ mu}$ $\ mu$ , что это будет ошибочно; 0 будет заменено на 1 или наоборот. Давайте проигнорируем двойные мутации и гибель молекул (популяция будет расти бесконечно), и разделите восемь молекул на три класса в зависимости от их расстояния Хэмминга от основной последовательности:

Хэмминга. расстояние	Последовательность (и)
0	[000]
1	[001]. [010]. [100]
2	[110]. [101 ]. [011]
3	[111]

Обратите внимание, что количество последовательностей для расстояния d - это просто биномиальный коэффициент $(L d) {\ displaystyle {\ tbinom { L} {d}}}$ ${\ tbinom Ld}$ для L = 3, и что каждая последовательность может быть визуализирована как вершина L = 3-мерного куба, причем каждое ребро куба указывает путь мутации, в котором происходит изменение Расстояние Хэмминга равно нулю или ± 1. Можно видеть, что, например, одна треть мутаций молекул [001] будет производить [000] молекул, в то время как другие две трети будут производить молекулы класса 2 [011] и [101]. Теперь мы можем записать выражение для дочерних популяций $ni ′ {\ displaystyle n '_ {i}}$ $n'_{i}$ класса i в терминах родительских популяций $nj {\ displaystyle n_ {j }}$ $n_ {j}$ .

ni ′ = ∑ j = 0 3 wijnj {\ displaystyle n '_ {i} = \ sum _ {j = 0} ^ {3} w_ {ij} n_ {j}}

n'_{i}=\sum _{{j=0}}^{3}w_{{ij}}n_{j}

где матрица 'w', которая включает естественный отбор и мутацию, согласно квазивидовой модели, определяется как:

w = [a ⋅ Q 3 a ⋅ μ 0 0 μ Q 2 μ 0 0 2 μ Q μ 0 0 3 μ Q] {\ displaystyle \ mathbf {w} = {\ begin {bmatrix} a \ cdot Q 3a \ cdot \ mu 0 0 \\\ mu Q 2 \ mu 0 \\ 0 2 \ mu Q \ mu \\ 0 0 3 \ mu Q \ end {bmatrix}}}

{\ mathbf {w}} = {\ begin {bmatrix} a \ cdot Q 3a \ cdot \ mu 0 0 \\\ mu Q 2 \ mu 0 \\ 0 2 \ mu Q \ mu \\ 0 0 3 \ mu Q \ end { bmatrix}}

где $Q = (1 - μ) L {\ displaystyle Q = (1- \ mu) ^ {L}}$ $Q = (1- \ mu) ^ {L}$ - вероятность что вся молекула будет успешно воспроизведена. собственные векторы матрицы w будут давать значения равновесной совокупности для каждого класса. Например, если скорость мутации μ равна нулю, у нас будет Q = 1, а равновесные концентрации будут $[n 0, n 1, n 2, n 3] = [1, 0, 0, 0] {\ displaystyle [n_ {0}, n_ {1}, n_ {2}, n_ {3}] = [1,0,0,0]}$ $[n_ {0}, n_ {1}, n_ {2}, n_ {3}] = [1,0, 0,0]$ . Мастер-последовательность, будучи сильнейшим, останется в живых. Если у нас есть точность репликации Q = 0,95 и генетическое преимущество a = 1,05, то равновесные концентрации будут примерно $[0,33, 0,38, 0,24, 0,06] {\ displaystyle [0,33,0.38,0.24,0.06]}$ $[0.33,0.38,0.24,0.06]$ . Видно, что основная последовательность не так доминирует; тем не менее, последовательности с малым расстоянием Хэмминга составляют большинство. Если точность репликации Q приближается к 0, то равновесные концентрации будут примерно $[0,125, 0,375, 0,375, 0,125] {\ displaystyle [0,125,0,375,0,375,0,125]}$ $[0,125,0,375,0,375,0,125]$ . Это совокупность с равным количеством каждой из 8 последовательностей. (Если бы у нас была совершенно равная популяция всех последовательностей, у нас была бы популяция [1,3,3,1] / 8.)

Если мы теперь перейдем к случаю, когда количество пар оснований велико, скажем, L = 100, мы получаем поведение, напоминающее фазовый переход . На графике ниже слева показан ряд равновесных концентраций, разделенных на биномиальный коэффициент $(100 k) {\ displaystyle {\ tbinom {100} {k}}}$ ${\ tbinom {100} k}$ . (Это умножение покажет совокупность для отдельной последовательности на этом расстоянии и даст плоскую линию для равного распределения.) Селективное преимущество основной последовательности установлено на a = 1.05. По горизонтальной оси отложено расстояние Хэмминга d. Различные кривые относятся к разной общей частоте мутаций $(1 - Q) {\ displaystyle (1-Q)}$ $(1-Q)$ . Видно, что при низких значениях общей частоты мутаций популяция состоит из квазивидов, собранных в окрестности основной последовательности. Выше общей скорости мутаций примерно 1-Q = 0,05 распределение быстро распространяется, чтобы заполнить все последовательности одинаково. На графике ниже справа показана фракционная популяция основной последовательности как функция общей скорости мутаций. Снова видно, что ниже критической скорости мутации примерно 1-Q = 0,05 основная последовательность содержит большую часть популяции, а выше этой скорости она содержит только примерно $2-L ≈ 10-30 {\ displaystyle 2 ^ {- L} \ около 10 ^ {- 30}}$ $2 ^ {{- L}} \ приблизительно 10 ^ {{- 30}}$ от всего населения.

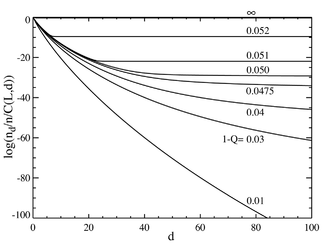
Численность популяции как функция расстояния Хэмминга d и частоты мутаций (1-Q). Горизонтальная ось d - это расстояние Хэмминга молекулярных последовательностей от основной последовательности. Вертикальная ось представляет собой логарифм совокупности для любой последовательности на этом расстоянии, деленный на общую совокупность (таким образом, деление n d на биномиальный коэффициент). Общее количество цифр на последовательность L = 100, и основная последовательность имеет избирательное преимущество a = 1,05.

Популяция основной последовательности как доля от общей популяции (n) как функция общей мутации ставка (1-Q). Общее количество цифр в последовательности L = 100, а основная последовательность имеет избирательное преимущество a = 1,05. Видно, что «фазовый переход» происходит примерно при 1-Q = 0,05.

Можно видеть, что существует резкий переход при значении 1-Q, немного превышающем 0,05. При частоте мутаций выше этого значения популяция основной последовательности падает практически до нуля. Выше этого значения он доминирует.

В пределе, когда L приближается к бесконечности, система действительно имеет фазовый переход при критическом значении Q: $Q c = 1 / a. {\ displaystyle Q_ {c} = 1 / a.}$ $Q_ {c} = 1 / a.$ . Можно представить себе общую скорость мутации (1-Q) как своего рода «температуру», которая «плавит» верность молекулярных последовательностей выше критической «температуры» $1 - Q c {\ displaystyle 1- Q_ {c}}$ $1-Q_ {c}$ . Для точной репликации информация должна быть «заморожена» в геноме.

См. Также

Литература

Эйген, М. (1971). «Самоорганизация вещества и эволюция биологических макромолекул». Naturwissenschaften. 58 (10): 465–523. Bibcode : 1971NW..... 58..465E. doi : 10.1007 / BF00623322. PMID 4942363. S2CID 38296619.
«Теория квазивидов в контексте популяционной генетики - Клаус О. Вилке» (PDF). Получено 12 октября 2005 г.
Campos, P.R.A.; Фонтанари, Дж. Ф. (1999). «Масштабирование конечного размера перехода порога ошибки в конечных совокупностях» (PDF). J. Phys. A: Математика. Gen. 32 : L1 – L7. arXiv : cond-mat / 9809209. Bibcode : 1999JPhA... 32L... 1C. doi : 10.1088 / 0305-4470 / 32/1/001. S2CID 16500591.
Холмс, Эдвард К. (2005). «Правильный размер». Генетика природы. 37 (9): 923–924. doi : 10.1038 / ng0905-923. PMC 7097767. PMID 16132047.
Эёрс Сатмари; Джон Мейнард Смит (1995). «Основные эволюционные переходы». Природа. 374 (6519): 227–232. Bibcode : 1995Natur.374..227S. doi : 10.1038 / 374227a0. PMID 7885442. S2CID 4315120.
Луис Вильярреал; Гюнтер Витцани (2013). «Переосмысление теории квазивидов: от наиболее приспособленных к совместным консорциумам». Всемирный журнал биологической химии. 4 (4): 79–90. doi : 10.4331 / wjbc.v4.i4.79. PMC 3856310. PMID 24340131.
Адам Кун; Мауро Сантос; Эёрс Сатмари (2005). «Настоящие рибозимы предполагают более низкий порог ошибки». Генетика природы. 37 (9): 1008–1011. doi : 10.1038 / ng1621. PMID 16127452. S2CID 30582475.