Войти
Общие вращения дерева. В дискретной математике, вращение дерева является операция над двоичным деревом , которая изменяет структуру, не влияя на порядок элементов. Вращение дерева перемещает один узел вверх по дереву и один узел вниз. Он используется для изменения формы дерева и, в частности, для уменьшения его высоты путем перемещения меньших поддеревьев вниз и более крупных поддеревьев вверх, что приводит к повышению производительности многих операций с деревом.
Существует несоответствие в различных описаниях определения направления вращения . Некоторые говорят, что направление вращения отражает направление, в котором узел движется при вращении (левый дочерний элемент, вращающийся в положение своего родителя, является правым вращением), в то время как другие говорят, что направление вращения отражает, какое поддерево вращается (левое поддерево, вращающееся в расположение его родителя - левое вращение, противоположное предыдущему). В этой статье используется подход направленного движения вращающегося узла.
Операция поворота вправо, как показано на соседнем изображении, выполняется с Q в качестве корня и, следовательно, является поворотом вправо или с корнем в Q. Эта операция приводит к повороту дерева в по часовой стрелке. Обратной операцией является левое вращение, которое приводит к движению против часовой стрелки (левое вращение, показанное выше, основано на P). Ключом к пониманию того, как работает вращение, является понимание его ограничений. В частности, порядок листьев дерева (например, при чтении слева направо) не может измениться (другой способ думать об этом - это то, что порядок, в котором листья будут посещаться при обходе по порядку, должен быть таким же после операция как раньше). Еще одно ограничение - это главное свойство двоичного дерева поиска, а именно то, что правый дочерний элемент больше, чем родительский, а левый дочерний элемент меньше, чем родительский элемент . Обратите внимание, что правый дочерний элемент левого дочернего элемента корня поддерева (например, узел B на диаграмме для дерева с корнем Q) может стать левым дочерним элементом корня, который сам становится правым дочерним элементом " new "корень повернутого поддерева, не нарушая ни одного из этих ограничений. Как видно на диаграмме, порядок листьев не меняется. Противоположная операция также сохраняет порядок и является вторым видом вращения.
Предполагая, что это двоичное дерево поиска, как указано выше, элементы должны интерпретироваться как переменные, которые можно сравнивать друг с другом. Буквенные символы слева используются в качестве заполнителей для этих переменных. В анимации справа заглавные буквенные символы используются в качестве заполнителей переменных, а строчные греческие буквы являются заполнителями для всего набора переменных. Кружки представляют отдельные узлы, а треугольники - поддеревья. Каждое поддерево может быть пустым, состоять из одного узла или состоять из любого количества узлов.
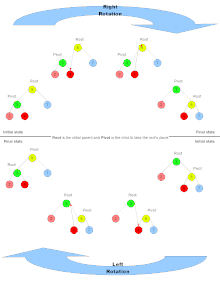Наглядное описание того, как выполняются вращения. Когда поддерево вращается, сторона поддерева, на которой оно вращается, увеличивает свою высоту на один узел, в то время как другое поддерево уменьшает свою высоту. Это делает вращение дерева полезным для балансировки дерева.
Рассмотрим терминологию Root для родительского узла поддеревьев, подлежащих вращению, Pivot для узла, который станет новым родительским узлом, RS для стороны вращения и OS для противоположной стороны вращения. Для корня Q на диаграмме выше, RS - это C, а OS - это P. Используя эти термины, псевдокод для вращения:
Pivot = Root.OS Root.OS = Pivot.RS Pivot.RS = Root Root = Pivot
Это операция с постоянным временем.
Программист также должен убедиться, что родительский элемент корня указывает на точку поворота после поворота. Также программист должен учитывать, что эта операция может привести к новому корню для всего дерева, и позаботиться об обновлении указателей соответственно.
Вращение дерева визуализирует обход двоичного дерева в инвариантном порядке. Это означает, что порядок элементов не изменяется при вращении любой части дерева. Вот порядок обхода показанных выше деревьев:
Левое дерево: ((A, P, B), Q, C) Правое дерево: (A, P, (B, Q, C))
Вычислить одно из другого очень просто. Ниже приведен пример кода Python, который выполняет это вычисление:
def right_rotation (treenode): left, Q, C = treenode A, P, B = left return (A, P, (B, Q, C))
Другой способ взглянуть на это:
Правый поворот узла Q:
Пусть P будет левым потомком Q. Установите левый дочерний элемент Q как правого ребенка P. [Установить родителя правого потомка P равным Q] Установить правого потомка P равным Q. [Установить родителя Q равным P]
Поворот узла P влево:
Пусть Q будет правым потомком P. Сделайте правого потомка P левым потомком Q. [Установить для левого дочернего элемента Q значение P] Установить для левого дочернего элемента Q значение P. [Установить для родительского элемента P значение Q]
Все остальные соединения остаются как есть.
Есть также двойные вращения, которые представляют собой комбинацию левого и правого вращения. Двойное левое вращение в X можно определить как правое вращение у правого дочернего элемента X, за которым следует левое вращение в X; аналогично, двойное правое вращение в X можно определить как левое вращение у левого дочернего элемента X, за которым следует правое вращение в X.
Вращения дерева используются в ряде древовидных структур данных, например, деревья AVL, красно-черные деревья, растопыренные деревья и трепы. Для них требуется только постоянное время, поскольку они являются локальными преобразованиями: они работают только на 5 узлах и не нуждаются в проверке остальной части дерева.
Наглядное описание того, как повороты вызывают перебалансировку в дереве AVL. Дерево можно перебалансировать с помощью вращений. После вращения сторона вращения увеличивает свою высоту на 1, в то время как сторона, противоположная вращению, уменьшает свою высоту аналогичным образом. Следовательно, можно стратегически применять вращения к узлам, левый и правый дочерние узлы которых отличаются по высоте более чем на 1. Самобалансирующиеся деревья двоичного поиска применяют эту операцию автоматически. Типом дерева, в котором используется этот метод перебалансировки, является дерево AVL.
 | Нерешенная проблема в информатике :. Можно ли вычислить расстояние вращения между двумя двоичными деревьями за полиномиальное время? ( больше нерешенных проблем в информатике) |
Расстояние поворота между любыми двумя двоичными деревьями с одинаковым количеством узлов - это минимальное количество оборотов, необходимых для преобразования одного в другой. При таком расстоянии набор двоичных деревьев с n узлами становится метрическим пространством : расстояние является симметричным, положительным, когда заданы два разных дерева, и удовлетворяет неравенству треугольника .
Это открытая проблема, существует ли алгоритм полиномиального времени для вычисления расстояния вращения.
Дэниел Слейатор, Роберт Тарджан и Уильям Терстон показали, что расстояние вращения между любыми двумя деревьями с n-узлами (для n ≥ 11) не превышает 2n - 6, и что некоторые пары деревьев так далеко друг от друга, если n достаточно велико. Лайонел Пурнин показал, что на самом деле такие пары существуют всякий раз, когда n ≥ 11.
