Азартные игры и теория информации

Статистический вывод можно рассматривать как теорию азартных игр, применяемую к окружающему нас миру. Множество приложений для логарифмических показателей информации точно подсказывают нам, как сделать наилучшее предположение перед лицом неполной информации. В этом смысле теория информации может считаться формальным выражением теории азартных игр. Поэтому неудивительно, что теория информации имеет приложения к азартным играм.

• 1 Ставки Келли
  • 1.1 Дополнительная информация
  • 1.2 Скорость удвоения
  • 1.3 Ожидаемая прибыль
• 2 Приложения для самоинформации
• 3 Приложения в азартных играх
• 4 См. также
• 5 Ссылки
• 6 Внешние ссылки

Ставки Келли или пропорциональные ставки - это приложение От теории информации до инвестирования и азартных игр. Его первооткрывателем был Джон Ларри Келли-младший..

Часть идеи Келли заключалось в том, чтобы игрок максимизировал математическое ожидание логарифма своего капитала, а не ожидаемую прибыль от каждой ставки. Это важно, так как в последнем случае человек будет вынужден поставить все, что у него есть, когда ему будет предложена выгодная ставка, а если он проиграет, у него не будет капитала для последующих ставок. Келли понял, что это логарифм капитала игрока, который складывается в последовательных ставках и «к которому применяется закон больших чисел».

Дополнительная информация

A бит - это количество энтропии в событии с таблицей ставок с двумя возможными исходами и четными коэффициентами. Очевидно, мы могли бы удвоить наши деньги, если бы знали заранее, каков будет исход этого события. Келли пришел к выводу, что независимо от того, насколько сложен сценарий ставок, мы можем использовать оптимальную стратегию ставок, называемую критерием Келли, чтобы наши деньги расти экспоненциально с любой дополнительной информацией, которую мы можем получить. Значение этой «незаконной» дополнительной информации измеряется как взаимная информация относительно результата события, на которое можно сделать ставку:

$I\; (X;\; Y)\; =\; EY\; \{DKL\; (P\; (X\; |\; Y)\; \Vert \; P\; (X\; |\; I))\}\; =\; EY\; \{DKL\; (P\; (X\; |\; сторона\; \backslash \; информация\; \backslash \; Y)\; \Vert \; P\; (X\; |\; заявлено\; \backslash \; шансы\; \backslash \; I))\},\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; I\; (X;\; Y)\; =\; \backslash \; mathbb\; \{E\}\; \_\; \{Y\}\; \backslash \; \{D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; \{\backslash \; big\; (\}\; P\; (X\; |\; Y)\; \backslash \; |\; P\; (X\; |\; I)\; \{\backslash \; big)\}\; \backslash \}\; \backslash \; \backslash \; =\; \backslash \; mathbb\; \{E\}\; \_\; \{Y\}\; \backslash \; \{D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; \{\backslash \; big\; (\}\; P\; (X\; |\; \{\backslash \; textrm\; \{side\; \backslash \; information\; \backslash \}\}\; Y)\; \backslash \; |\; P\; (X\; |\; \{\; \backslash \; textrm\; \{указано\; \backslash \; odds\; \backslash \}\}\; I)\; \{\backslash \; big)\}\; \backslash \},\; \backslash \; end\; \{align\}\}\}$

где Y - дополнительная информация, X - результат события, на которое можно сделать ставку, а I - состояние знаний букмекера. Это среднее расхождение Кульбака – Лейблера, или информационный выигрыш, для апостериорного распределения вероятностей X при значении Y относительно априорного распределения. или заявленные шансы на X. Обратите внимание, что ожидание берется за Y, а не за X: нам нужно оценить, насколько точна в долгосрочной перспективе наша дополнительная информация Y, прежде чем мы начнем делать ставки реальными деньгами на X. Это простой применение байесовского вывода. Обратите внимание, что дополнительная информация Y может повлиять не только на наши знания о событии X, но и на само событие. Например, Y может означать лошадь, у которой слишком много овса или недостаточно воды. Та же самая математика применима и в этом случае, потому что с точки зрения букмекера, случайные фиксации гонок уже учитываются, когда он рассчитывает свои коэффициенты.

Природа дополнительной информации чрезвычайно привередлива. Мы уже видели, что это может повлиять на фактическое событие, а также на наши знания о результате. Предположим, у нас есть информатор, который сообщает нам, что определенная лошадь собирается победить. Мы, конечно, не хотим ставить все наши деньги на эту лошадь только на слух: этот информатор может делать ставку на другую лошадь и, возможно, распространяет слухи только для того, чтобы самому получить лучшие шансы. Вместо этого, как мы указали, нам необходимо оценить нашу дополнительную информацию в долгосрочной перспективе, чтобы увидеть, как она соотносится с результатами гонок. Таким образом, мы можем точно определить, насколько надежен наш информатор, и сделать ставки именно так, чтобы максимизировать ожидаемый логарифм нашего капитала в соответствии с критерием Келли. Даже если наш информатор лжет нам, мы все равно можем извлечь выгоду из его лжи, если сможем найти некоторую обратную корреляцию между его подсказками и фактическими результатами гонки.

Коэффициент удвоения

Коэффициент удвоения при игре в азартные игры на скачках равен

$W\; (b,\; p)\; =\; E\; [log\; 2\; \; S\; (X)]\; =\; \sum \; я\; знак\; равно\; 1\; Mpi\; журнал\; 2\; \; bioi\; \{\backslash \; Displaystyle\; W\; (b,\; p)\; =\; \backslash \; mathbb\; \{E\}\; [\backslash \; log\; \_\; \{2\}\; S\; (X)]\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{m\}\; p\_\; \{i\}\; \backslash \; log\; \_\; \{2\}\; b\_\; \{i\}\; o\_\; \{i\}\}$

где есть $m\; \{\backslash \; displaystyle\; m\}$лошадей, вероятность $i\; \{\; \backslash \; displaystyle\; i\}$выигрыш лошади равен $pi\; \{\backslash \; displaystyle\; p\_\; \{i\}\}$, доля богатства, поставленная на лошадь, равна $bi\; \{\backslash \; displaystyle\; b\_\; \{i\}\}$, и шансы (выплата) будут $oi\; \{\backslash \; displaystyle\; o\_\; \{i\}\}$(например, $oi\; =\; 2\; \{\backslash \; displaystyle\; o\_\; \{i\}\; =\; 2\}$, если для $i\; \{\backslash \; displaystyle\; i\}$ой лошади выплачивается двойная ставка). Это количество максимизируется пропорциональной (Келли) игрой:

$b\; =\; p\; \{\backslash \; displaystyle\; b\; =\; p\; \backslash ,\}$

, для которого

$max\; b\; W\; (b,\; p)\; =\; \sum \; ipi\; log\; 2\; \; oi\; -\; ЧАС\; (п)\; \{\backslash \; displaystyle\; \backslash \; max\; \_\; \{b\}\; W\; (b,\; p)\; =\; \backslash \; sum\; \_\; \{i\}\; p\_\; \{i\}\; \backslash \; log\; \_\; \{2\}\; o\_\; \{i\}\; -H\; (p)\; \backslash ,\}$

где $H\; (p)\; \{\backslash \; displaystyle\; H\; (p)\}$- информационная энтропия.

Ожидаемый выигрыш

Существует важное, но простое соотношение между количеством дополнительная информация, которую получает игрок, и ожидаемый экспоненциальный рост его капитала (Келли):

$E\; log\; \; K\; t\; =\; log\; \; K\; 0\; +\; \sum \; i\; =\; 1\; t\; H\; i\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{E\}\; \backslash \; log\; K\_\; \{\; t\}\; =\; \backslash \; log\; K\_\; \{0\}\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{t\}\; H\_\; \{i\}\}$

для оптимальной стратегии ставок, где $K\; 0\; \{\backslash \; displaystyle\; K\_\; \{0\}\}$- начальная столица, $K\; t\; \{\backslash \; displaystyle\; K\_\; \{t\}\}$- капитал после t-й ставки, а $H\; i\; \{\backslash \; displaystyle\; H\_\; \{i\; \}\}$- количество дополнительной информации, полученной относительно i-й ставки (в частности, взаимная информация относительно результата каждого события, на которое можно сделать ставку). Это уравнение применяется при отсутствии каких-либо транзакционных издержек или минимальных ставок. Когда применяются эти ограничения (что неизменно происходит в реальной жизни), в игру вступает еще одна важная концепция азартных игр: игрок (или недобросовестный инвестор) должен столкнуться с определенной вероятностью окончательного разорения, которая известна как разорение игрока сценарий. Обратите внимание, что даже продукты питания, одежда и жилье могут считаться фиксированными операционными издержками и, таким образом, увеличивать вероятность окончательного разорения игрока.

Это уравнение было первым применением теории информации Шеннона за пределами ее преобладающей парадигмы передачи данных (Пирс).

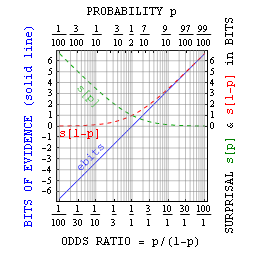
Неожиданность и свидетельство в битах, как логарифмические меры вероятности и шансов соответственно.

Логарифмическая вероятностная мера самоинформация или неожиданность, среднее значение которой информационная энтропия / неопределенность, средняя разность которой составляет KL-дивергенция, сама по себе имеет приложения для анализа вероятностей. Две его основные сильные стороны заключаются в том, что неожиданности: (i) уменьшают мизерные вероятности до числа управляемого размера, и (ii) добавляют всякий раз, когда вероятности умножаются.

Например, можно сказать, что «количество состояний равно двум количеству битов», т.е. #states = 2. Здесь величина, измеряемая в битах, является логарифмической мерой информации, упомянутой выше. Следовательно, выпадение всех орлов после первого подбрасывания N монет вызывает N неожиданностей.

Аддитивная природа сюрпризов и способность почувствовать их значение с помощью горстки монет могут помочь поместить невероятные события (например, выигрыш в лотерею или несчастный случай) в контекст. Например, если один из 17 миллионов билетов является победителем, то неожиданность выигрыша от одного случайного выбора составляет около 24 бит. Несколько раз бросив 24 монеты, вы почувствуете сюрприз, когда все решится с первого раза.

Аддитивный характер этой меры также пригодится при взвешивании альтернатив. Например, представьте, что неожиданность вреда от вакцинации составляет 20 бит. Если неожиданность выявления болезни без вакцинации составляет 16 бит, но неожиданность вреда от болезни, если вы ее поймаете, составляет 2 бита, тогда неожиданность вреда от НЕ получения вакцинации составляет всего 16 + 2 = 18 бит. Независимо от того, решите вы пройти вакцинацию или нет (например, денежные затраты на ее оплату не включены в это обсуждение), вы можете, по крайней мере, принять на себя ответственность за решение, основанное на том, что отказ от вакцинации требует большего, чем немного дополнительного риска.

В более общем смысле, можно связать вероятность p с битами неожиданных sbit как вероятность = 1/2. Как было предложено выше, это в основном полезно с малыми вероятностями. Однако Джейнс указал, что с помощью утверждений истина-ложь можно также определить биты доказательств ebits как неожиданность против минус неожиданность за. Это свидетельство в битах относится просто к отношению шансов = p / (1-p) = 2 и имеет преимущества, аналогичные преимуществам самой самоинформации.

Теорию информации можно рассматривать как способ количественной оценки информации, чтобы принять лучшее решение перед лицом несовершенной информации. То есть как принять наилучшее решение, используя только имеющуюся у вас информацию. Смысл ставок состоит в том, чтобы рационально оценить все соответствующие переменные неопределенной игры / расы / матча, затем сравнить их с оценками букмекерской конторы, которые обычно представлены в форме коэффициентов или спредов, и сделать правильную ставку, если оценки существенно различаются. Сфера азартных игр, где это используется больше всего, - это ставки на спорт. Спортивные увечья очень хорошо поддаются теории информации из-за доступности статистики. В течение многих лет известные экономисты проверяли различные математические теории, используя спорт в качестве лаборатории, с очень разными результатами.

Согласно одной из теорий ставок на спорт, это случайное блуждание. Случайное блуждание - это сценарий, при котором новая информация, цены и доходность будут колебаться случайно, это часть гипотезы эффективного рынка. Основное убеждение в гипотезе эффективного рынка состоит в том, что рынок всегда будет вносить корректировки в соответствии с любой новой информацией. Следовательно, никто не может превзойти рынок, потому что он торгует на той же информации, на которой рынок корректировался. Однако, по мнению Фамы, для создания эффективного рынка необходимо соблюдение трех качеств:

• Торговля ценными бумагами не связана с транзакционными издержками
• Вся доступная информация бесплатно доступна для всех участников рынка
• Все согласны с тем, что текущая информация влияет на текущую цену и распределение будущих цен каждой ценной бумаги.

Статистики показали, что это третье условие, позволяющее использовать теорию информации в борьбе с физическими недостатками в спорте. Когда все не согласны с тем, как информация повлияет на исход события, мы получаем разные мнения.

• Принцип безразличия
• Статистические прогнозы футбольных ассоциаций
• Расширенная статистика НФЛ

• Статистический анализ в моделях спортивного гандикапа
• DVOA как независимая переменная