Вейвлет Добеши

Ортогональные вейвлеты 2-мерный вейвлет Добеши 20 (Вейвлет Fn X Scaling Fn)

Вейвлеты Добеши, основанные на работе Ингрид Добеши, представляют собой семейство ортогональных вейвлетов, определяющих дискретное вейвлет-преобразование и характеризующихся максимальным числом исчезающих моментов для некоторого заданного поддерживают. Для каждого типа вейвлетов этого класса существует функция масштабирования (называемая исходным вейвлетом), которая генерирует ортогональный анализ с множественным разрешением.

• 1 Свойства
• 2 Конструкция
• 3 Масштабирующие последовательности наименьший порядок аппроксимации
• 4 Реализация
  • 4.1 Преобразование, D4
  • 4.2 Обратное преобразование, D4
• 5 См. также
• 6 Ссылки
• 7 Внешние ссылки

В общем, вейвлеты Добеши выбираются так, чтобы иметь наибольшее число A исчезающих моментов (это не означает наилучшую гладкость) для данной ширины опоры (числа коэффициентов) 2A. Используются две схемы именования: DN с использованием длины или количества ответвлений и dbA со ссылкой на количество исчезающих моментов. Итак, D4 и db2 - это одно и то же вейвлет-преобразование.

Среди 2 возможных решений алгебраических уравнений для условий момента и ортогональности выбирается то, масштабный фильтр которого имеет экстремальную фазу. Вейвлет-преобразование также легко реализовать на практике с помощью быстрого вейвлет-преобразования. Вейвлеты Добеши широко используются для решения широкого круга задач, например свойства самоподобия сигнала или фрактальные проблемы, неоднородности сигнала и т.д.

Вейвлеты Добеши не определены в терминах результирующих функций масштабирования и вейвлетов; фактически, их невозможно записать в закрытой форме. Графики ниже созданы с использованием каскадного алгоритма , числового метода, состоящего из обратного преобразования [1 0 0 0 0...] подходящее количество раз.

масштабные и вейвлет-функции
амплитуды частотных спектров вышеуказанных функций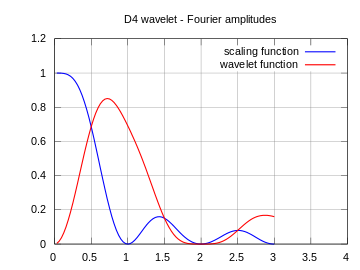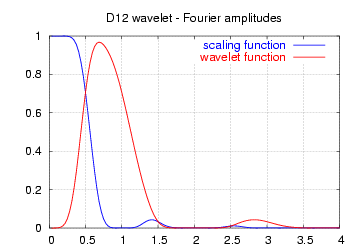

Обратите внимание, что представленные здесь спектры не являются частотными характеристиками фильтров высоких и низких частот, а скорее амплитудами непрерывных преобразований Фурье. масштабных (синий) и вейвлет (красный) функций.

Ортогональные вейвлеты Добеши D2 – D20 соотв. Обычно используются db1 – db10. Номер индекса относится к количеству N коэффициентов. Каждый вейвлет имеет количество нулевых моментов или исчезающих моментов, равное половине числа коэффициентов. Например, D2 имеет один исчезающий момент, D4 - два и т. Д. Исчезающий момент ограничивает способность вейвлетов представлять поведение или информацию полинома в сигнале. Например, D2 с одним нулевым моментом легко кодирует полиномы одного коэффициента или постоянные составляющие сигнала. D4 кодирует полиномы с двумя коэффициентами, то есть постоянной и линейной составляющими сигнала; и D6 кодирует 3-полиномы, то есть постоянные, линейные и квадратичные компоненты сигнала. Эта способность кодировать сигналы, тем не менее, зависит от явления масштабной утечки и отсутствия инвариантности сдвига, которые возникают из-за операции дискретного сдвига (ниже) во время применения преобразования. Подпоследовательности, которые представляют линейные, квадратичные (например) компоненты сигнала, обрабатываются преобразованием по-разному в зависимости от того, совпадают ли точки с точками с четными или нечетными номерами в последовательности. Отсутствие важного свойства инвариантности сдвига привело к разработке нескольких различных версий инвариантного сдвига (дискретного) вейвлет-преобразования.

Оба масштабирующая последовательность (фильтр нижних частот) и последовательность вейвлетов (полосовой фильтр) (см. ортогональный вейвлет для деталей этой конструкции) здесь будут нормализованы, чтобы иметь сумму, равную 2, и сумму квадратов, равную 2. В некоторых приложениях они нормализованы до суммы $2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{2\}\}\}$, так что обе последовательности и все их сдвиги на четное число коэффициентов ортонормированы. друг другу.

Использование общего представления для масштабирующей последовательности ортогонального дискретного вейвлет-преобразования с порядком аппроксимации A,

$a\; (Z)\; =\; 2\; 1\; -\; A\; (1\; +\; Z)\; A\; p\; (Z),\; \{\backslash \; displaystyle\; a\; (Z)\; =\; 2\; ^\; \{1-A\}\; (1\; +\; Z)\; ^\; \{A\}\; p\; (Z),\}$

с N = 2A, p с действительными коэффициентами, p (1) = 1 и deg ( p) = A - 1, можно записать условие ортогональности как

$a\; (Z)\; a\; (Z\; -\; 1)\; +\; a\; (-\; Z)\; a\; (-\; Z\; -\; 1)\; =\; 4,\; \{\backslash \; displaystyle\; a\; (Z)\; a\; \backslash \; left\; (Z\; ^\; \{-\; 1\}\; \backslash \; right)\; +\; a\; (-Z)\; a\; \backslash \; left\; (-Z\; ^\; \{-\; 1\}\; \backslash \; right)\; =\; 4,\}$

или равно как

$(2\; -\; X)\; AP\; (X)\; +\; XAP\; (2\; -\; X)\; =\; 2\; A\; (*),\; \{\backslash \; displaystyle\; (2-X)\; ^\; \{A\}\; P\; (X)\; +\; X\; ^\; \{A\}\; P\; (2-X)\; =\; 2\; ^\; \{A\}\; \backslash \; qquad\; (*),\}$

с полиномом Лорана

$X:\; =\; 1\; 2\; (2\; -\; Z\; -\; Z\; -\; 1)\; \{\backslash \; displaystyle\; X:\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\; \}\; \backslash \; left\; (2-ZZ\; ^\; \{-\; 1\}\; \backslash \; right)\}$

генерирует все симметричные последовательности и $X\; (-\; Z)\; =\; 2\; -\; X\; (Z).\; \{\backslash \; displaystyle\; X\; (-Z)\; =\; 2-X\; (Z).\}$Далее, P (X) обозначает симметричный полином Лорана

$P\; (X\; (Z))\; =\; p\; (Z)\; p\; (Z\; -\; 1).\; \{\backslash \; Displaystyle\; P\; (X\; (Z))\; =\; p\; (Z)\; p\; \backslash \; left\; (Z\; ^\; \{-\; 1\}\; \backslash \; right).\}$

Поскольку

$X\; (eiw)\; =\; 1\; -\; cos\; \; (w)\; \{\; \backslash \; Displaystyle\; Икс\; (е\; ^\; \{iw\})\; =\; 1-\; \backslash \; cos\; (w)\}$

$p\; (eiw)\; p\; (e\; -\; iw)\; =\; |\; п\; (е\; я\; ш)\; |\; 2\; \{\backslash \; displaystyle\; p\; (e\; ^\; \{iw\})\; p\; (e\; ^\; \{-\; iw\})\; =\; |\; p\; (e\; ^\; \{iw\})\; |\; ^\; \{2\}\}$

P принимает неотрицательные значения на отрезке [0, 2].

Уравнение (*) имеет одно минимальное решение для каждого A, которое может быть получено делением в кольце усеченных степенных рядов в X,

$PA\; (X)\; =\; \sum \; k\; =\; 0\; A\; -\; 1\; (\; A\; +\; k\; -\; 1\; A\; -\; 1)\; 2\; -\; k\; X\; k.\; \{\backslash \; Displaystyle\; P\_\; \{A\}\; (X)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{A-1\}\; \{\backslash \; binom\; \{A\; +\; k-1\}\; \{A-1\}\}\; 2\; ^\; \{-\; k\}\; X\; ^\; \{\; k\}.\}$

Очевидно, это имеет положительные значения на (0,2).

Однородное уравнение для (*) антисимметрично относительно X = 1 и, следовательно, имеет общее решение

$XA\; (X\; -\; 1)\; R\; ((X\; -\; 1)\; 2),\; \{\backslash \; displaystyle\; X\; ^\; \{\; A\}\; (X-1)\; R\; \backslash \; left\; ((X-1)\; ^\; \{2\}\; \backslash \; right),\}$

, где R - некоторый многочлен с действительными коэффициентами. Сумма

$P\; (X)\; =\; PA\; (X)\; +\; XA\; (X\; -\; 1)\; R\; ((X\; -\; 1)\; 2)\; \{\backslash \; displaystyle\; P\; (X)\; =\; P\_\; \{A\}\; (X)\; +\; X\; ^\; \{\; A\}\; (X-1)\; R\; \backslash \; left\; ((X-1)\; ^\; \{2\}\; \backslash \; right)\}$

должно быть неотрицательным на интервале [0,2], переводится в набор линейных ограничений на коэффициенты R. Значения P на интервале [0,2] ограничены некоторой величиной $4\; A\; -\; r,\; \{\backslash \; displaystyle\; 4\; ^\; \{Ar\},\}$максимизация r приводит к линейной программе с бесконечно много условий неравенства.

Решить

$P\; (X\; (Z))\; =\; p\; (Z)\; p\; (Z\; -\; 1)\; \{\backslash \; displaystyle\; P\; (X\; (Z))\; =\; p\; (Z)\; p\; \backslash \; left\; (Z\; ^\; \{-1\}\; \backslash \; right)\}$

для p используется метод, называемый спектральной факторизацией, соответственно. Алгоритм Фейера-Рисса. Многочлен P (X) разбивается на линейные множители

$P\; (X)\; =\; (X\; -\; \mu \; 1)\; \cdots \; (X\; -\; \mu \; N),\; N\; =\; A\; +\; 1\; +\; 2\; deg\; \; (R).\; \{\backslash \; Displaystyle\; P\; (X)\; =\; (X-\; \backslash \; mu\; \_\; \{1\})\; \backslash \; cdots\; (X-\; \backslash \; mu\; \_\; \{N\}),\; \backslash \; qquad\; N\; =\; A\; +\; 1\; +\; 2\; \backslash \; deg\; (R).\}$

Каждый линейный множитель представляет собой многочлен Лорана

$X\; (Z)\; -\; \mu \; =\; -\; 1\; 2\; Z\; +\; 1\; -\; \mu \; -\; 1\; 2\; Z\; -\; 1\; \{\backslash \; displaystyle\; X\; (Z)\; -\; \backslash \; mu\; =\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; Z\; +\; 1-\; \backslash \; mu\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; Z\; ^\; \{-\; 1\}\}$

, который можно разложить на два линейных фактора. Можно сопоставить любой из двух линейных факторов с p (Z), таким образом, можно получить 2 возможных решения. Для экстремальной фазы выбирается тот, который имеет все комплексные корни p (Z) внутри или на единичной окружности и, таким образом, является действительным.

Для вейвлет-преобразования Добеши используется пара линейных фильтров. Эта пара фильтров должна обладать свойством, которое называется квадратурным зеркальным фильтром. Решение коэффициента линейного фильтра $ci\; \{\backslash \; displaystyle\; c\_\; \{i\}\}$с использованием свойства квадратурного зеркального фильтра приводит к приведенному ниже решению для значений коэффициентов для фильтра порядка 4.

$c\; 0\; =\; 1\; +\; 3\; 4\; 2,\; c\; 1\; =\; 3\; +\; 3\; 4\; 2,\; c\; 2\; =\; 3\; -\; 3\; 4\; 2,\; c\; 3\; =\; 1\; -\; 3\; 4\; 2.\; \{\backslash \; displaystyle\; c\_\; \{0\}\; =\; \{\backslash \; frac\; \{1\; +\; \{\backslash \; sqrt\; \{3\}\}\}\; \{4\; \{\backslash \; sqrt\; \{2\}\}\}\},\; \backslash \; quad\; c\_\; \{1\}\; =\; \{\backslash \; frac\; \{3\; +\; \{\backslash \; sqrt)\; \{3\}\}\}\; \{4\; \{\backslash \; sqrt\; \{2\}\}\}\},\; \backslash \; quad\; c\_\; \{2\}\; =\; \{\backslash \; frac\; \{3\; -\; \{\backslash \; sqrt\; \{3\}\}\}\; \{4\; \{\backslash \; sqrt\; \{2\}\}\}\},\; \backslash \; quad\; c\_\; \{3\}\; =\; \{\backslash \; frac\; \{1\; -\; \{\backslash \; sqrt\; \{3\}\}\}\; \{4\; \{\backslash \; sqrt\; \{2\}\}\}\}.\}$

Ниже приведены коэффициенты масштабных функций для D2-20. Вейвлет-коэффициенты получают, меняя порядок коэффициентов масштабирующей функции и затем меняя знак каждого второго (то есть вейвлет D4 = {-0,1830127, -0,3169873, 1,1830127, -0,6830127}). Математически это выглядит так: $bk\; =\; (-\; 1)\; ka\; N\; -\; 1\; -\; k\; \{\backslash \; displaystyle\; b\_\; \{k\}\; =\; (-\; 1)\; ^\; \{k\}\; a\_\; \{N-1-k\}\}$где k - индекс коэффициента, b - коэффициент вейвлет-последовательности и a - коэффициент масштабирующей последовательности. N - индекс вейвлета, т.е. 2 для D2.

Ортогональные коэффициенты Добеши (нормализованные до суммы 2)

D2 (Хаар )	D4	D6	D8	D10	D12	D14	D16	D18	D20
1	0,6830127	0,47046721	0,32580343	0,22641898	0,15774243	0,11009943	0,07695562	0,05385035	0,03771716
1	1,1830127	1,14111692	1,01094572	0,85394354	0,69950381	0,56079128	0,44246725	0,34483430	0,26612218
	0,3169873	0,650365	0,89220014	1,02432694	1,06226376	1,03114849	0,95548615	0,85534906	0,74557507
	-0,1830127	-0,19093442	-0,03957503	0,19576696	0,44583132	0,66437248	0,82781653	0,92954571	0,97362811
		-0,12083221	-0,26450717	-0,34265671	−0.31998660	-0,20351382	-0,02238574	0,18836955	0,39763774
		0,0498175	0,0436163	- 0,04560113	-0,18351806	-0,31683501	-0,40165863	-0,41475176	-0,35333620
			0,0465036	0,10970265	0,13788809	0,1008467	6,68194092 × 10	-0,13695355	-0,27710988
			-0,01498699	-0,00882680	0,03892321	0,11400345	0,18207636	0,21006834	0,18012745
				-0,01779187	-0,04466375	-0,05378245	-0,02456390	0,043452675	0,13160299
				4,71742793 × 10	7,83251152 × 10	-0,02343994	-0,06235021	-0,09564726	-0,10096657
					6,75606236 × 10	0,01774979	0,01977216	3,54892813 × 10	-0,04165925
					-1,52353381 × 10	6,07514995 × 10	0,01236884	0. 03162417	0,04696981
						−2,54790472 × 10	−6,88771926 × 10	−6,67962023 × 10	5,10043697 × 10
						5,00226853 × 10	−5,54004549 × 10	−6,05496058 × 10	−0,01517900
							9,55229711 × 10	2,61296728 × 10	1,97332536 × 10
							−1,66137261 × 10	3,25814671 × 10	2,81768659 × 10
								−3,56329759 × 10	−9,69947840 × 10
								5,5645514 × 10	-1,64709006 × 10
									1,32354367 × 10
									-1,875841 × 10

Части конструкции также используются для получения биортогональных вейвлетов Коэна-Добеши-Фово ( CDF).

Хотя программное обеспечение, такое как Mathematica, поддерживает вейвлеты Добеши напрямую, базовая реализация возможна в MATLAB (в данном случае, Добеши 4). Эта реализация использует периодизацию для решения проблемы сигналов конечной длины. Доступны и другие, более сложные методы, но часто в их использовании нет необходимости, поскольку они влияют только на самые концы преобразованного сигнала. Периодизация выполняется в прямом преобразовании непосредственно в векторной нотации MATLAB, а обратное преобразование - с использованием функции circshift ():

Transform, D4

Предполагается что S, вектор-столбец с четным числом элементов, был заранее определен как сигнал для анализа. Обратите внимание, что коэффициенты D4 равны [1 + √3, 3 + √3, 3 - √3, 1 - √3] / 4.

N = длина (S); s1 = S (1: 2: N - 1) + sqrt (3) * S (2: 2: N); d1 = S (2: 2: N) - sqrt (3) / 4 * s1 - (sqrt (3) - 2) / 4 * [s1 (N / 2); s1 (1: N / 2 - 1)]; s2 = s1 - [d1 (2: N / 2); d1 (1)]; s = (sqrt (3) - 1) / sqrt (2) * s2; d = - (sqrt (3) + 1) / sqrt (2) * d1;

Обратное преобразование, D4

d1 = d * ((sqrt (3) - 1) / sqrt (2)); s2 = s * ((sqrt (3) + 1) / sqrt (2)); s1 = s2 + circshift (d1, - 1); S (2: 2: N) = d1 + sqrt (3) / 4 * s1 + (sqrt (3) - 2) / 4 * circshift (s1, 1); S (1: 2: N - 1) = s1 - sqrt (3) * S (2: 2: N);

• Биномиальный QMF (Вейвлет-фильтры Добеши)
• Быстрое вейвлет-преобразование

• Дженсен; ла Кур-Харбо (2001). Рябь в математике. Берлин: Springer. С. 157–160. ISBN 3-540-41662-5.

• Цзяньхун (Джеки) Шен и Гилберт Стрэнг, прикладной и вычислительный гармонический анализ, 5 (3), Асимптотика фильтров Добеши, функций масштабирования и вейвлетов.

Викискладе есть медиафайлы, связанные с вейвлетами Добеши.

• Ингрид Добеши: десять лекций по вейвлетам, SIAM 1992
• AN Акансу, Эффективная структура QMF-вейвлетов (Binomial-QMF-вейвлеты Добеши), Proc. 1-й симпозиум NJIT по вейвлетам, апрель 1990 г.
• Proc. 1-й симпозиум NJIT по вейвлетам, поддиапазонам и преобразованиям, апрель 1990 г.
• А.Н. Акансу, Р.А. Хаддад и Х. Каглар, Биномиальное QMF-вейвлет-преобразование с совершенной реконструкцией, Proc. SPIE Визуальная коммуникация и обработка изображений, стр. 609–618, Лозанна, сентябрь 1990 г.
• Карлос Кабрелли, Урсула Молтер : обобщенное самоподобие ", Журнал математического анализа и приложений, 230: 251–260, 1999.
• Аппаратная реализация вейвлетов
• , Энциклопедия математики, EMS Press, 2001 [1994]
• И. Каплан, Вейвлет-преобразование Daubechies D4.