Периодограмма

В обработке сигналов периодограмма является оценкой спектральной плотности сигнала. Термин был введен Артуром Шустером в 1898 году. Сегодня периодограмма является составной частью более сложных методов (см. спектральная оценка ). Это наиболее распространенный инструмент для исследования амплитудно-частотных характеристик КИХ-фильтров и оконных функций. Анализаторы спектра БПФ также реализованы как временная последовательность периодограмм.

• 1 Определение
• 2 Вычисление
• 3 Приложения
• 4 См. Также
• 5 Примечания
• 6 Ссылки
• 7 Дополнительная литература

Сегодня используются как минимум два разных определения. Один из них предполагает усреднение по времени, а другой - нет. Усреднение по времени также входит в компетенцию других статей (метод Бартлетта и метод Уэлча ). Эта статья не об усреднении по времени. Представляющее интерес определение здесь состоит в том, что спектральная плотность мощности непрерывной функции, $x\; (t),\; \{\backslash \; displaystyle\; x\; (t),\}$, является преобразованием Фурье его автокорреляционная функция (см. Теорема взаимной корреляции ):

$F\; \{x\; (t)\; \ast \; x\; (-\; t)\}\; =\; X\; (f)\; \cdot \; X\; \ast \; (f)\; =\; |\; X\; (f)\; |\; 2.\; \{\backslash \; Displaystyle\; \{\backslash \; mathcal\; \{F\}\}\; \backslash \; \{Икс\; (Т)\; \backslash \; АСТ\; Икс\; (-t)\; \backslash \}\; =\; Икс\; (е)\; \backslash \; CDOT\; X\; ^\; \{*\}\; (е)\; =\; \backslash \; влево\; |\; Х\; (е)\; \backslash \; вправо\; |\; ^\; \{2\}.\}$

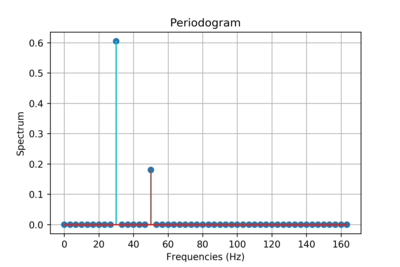Спектр мощности (квадрат величины) двух синусоидальных базисных функций, вычисленный методом периодограммы. Два спектра мощности (квадрат величины) (прямоугольный и квадрат Хэмминга оконные функции плюс фоновый шум), рассчитанные методом периодограмм.

При достаточно малых значениях параметра T можно наблюдать сколь угодно точное приближение для X (f) в области функции:

$X\; 1\; /\; T\; (f)\; =\; def\; \sum \; k\; =\; -\; \infty \; \infty \; X\; (f\; -\; k\; /\; T),\; \{\backslash \; displaystyle\; X\_\; \{1\; /\; T\}\; (f)\; \backslash \; \{\backslash \; stackrel\; \{\backslash \; text\; \{def\}\}\; \{=\}\}\; \backslash \; \backslash \; sum\; \_\; \{k\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; X\; \backslash \; left\; (fk\; /\; T\; \backslash \; right),\}$

что в точности определяется выборками x (nT), которые охватывают ненулевую длительность x (t) (см. преобразование Фурье с дискретным временем ).

И для достаточно больших значений параметра N $X\; 1\; /\; T\; (f)\; \{\backslash \; displaystyle\; X\_\; \{1\; /\; T\}\; (f)\}$может быть вычислено при произвольном близкую частоту суммированием вида:

$X\; 1\; /\; T\; (k\; NT)\; =\; \sum \; n\; =\; -\; \infty \; \infty \; T\; \cdot \; x\; (n\; T)\; ⏟\; x\; [n]\; \cdot \; e\; -\; i\; 2\; \pi \; kn\; N,\; \{\backslash \; displaystyle\; X\_\; \{1\; /\; T\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{k\}\; \{NT\}\}\; \backslash \; right)\; =\; \backslash \; sum\; \_\; \{n\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash \; underbrace\; \{T\; \backslash \; cdot\; x\; (nT)\}\; \_\; \{x\; [n]\}\; \backslash \; cdot\; e\; ^\; \{-\; i2\; \backslash \; pi\; \{\backslash \; frac\; \{kn\}\; \{N\}\}\},\}$

где k - целое число. Периодичность $e\; -\; i\; 2\; \pi \; kn\; N\; \{\backslash \; displaystyle\; e\; ^\; \{-\; i2\; \backslash \; pi\; \{\backslash \; frac\; \{kn\}\; \{N\}\}\}\}$позволяет очень просто записать это в терминах дискретного преобразования Фурье :

$X\; 1\; /\; T\; (k\; NT)\; =\; \sum \; nx\; N\; [n]\; \cdot \; e\; -\; i\; 2\; \pi \; kn\; N,\; ⏟\; DFT\; (сумма\; по\; любой\; n\; -последовательности\; длины\; N),\; \{\; \backslash \; Displaystyle\; X\_\; \{1\; /\; T\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{k\}\; \{NT\}\}\; \backslash \; right)\; =\; \backslash \; underbrace\; \{\backslash \; sum\; \_\; \{n\}\; x\; \_\; \{\_\; \{N\}\}\; [n]\; \backslash \; cdot\; e\; ^\; \{-\; i2\; \backslash \; pi\; \{\backslash \; frac\; \{kn\}\; \{N\}\}\},\}\; \_\; \{DFT\}\; \backslash \; quad\; \backslash \; scriptstyle\; \{\{\backslash \; text\; \{(сумма\; по\; любому\}\}\; n\; \{\backslash \; text\; \{-последовательность\; длины\}\}\; N)\},\; \}$

где $x\; N\; \{\backslash \; displaystyle\; x\; \_\; \{\_\; \{N\}\}\}$- периодическое суммирование: $x\; N\; [n]\; \triangleq \; \sum \; m\; =\; -\; \infty \; \infty \; x\; [n\; -\; м\; Н].\; \{\backslash \; displaystyle\; x\; \_\; \{\_\; \{N\}\}\; [n]\; \backslash \; \backslash \; треугольникq\; \backslash \; sum\; \_\; \{m\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; x\; [n-mN].\}$

При вычислении всех целых чисел k, между 0 и N-1, массив:

$S\; (k\; NT)\; =\; |\; \sum \; n\; x\; N\; [n]\; \cdot \; e\; -\; i\; 2\; \pi \; k\; n\; N\; |\; 2\; \{\backslash \; Displaystyle\; S\; \backslash \; left\; (\{\backslash \; tfrac\; \{k\}\; \{NT\}\}\; \backslash \; right)\; =\; \backslash \; left\; |\; \backslash \; sum\; \_\; \{n\}\; x\; \_\; \{\_\; \{N\}\}\; [n]\; \backslash \; cdot\; e\; ^\; \{-\; i2\; \backslash \; pi\; \{\backslash \; frac\; \{kn\}\; \{N\}\}\}\; \backslash \; right\; |\; ^\; \{2\}\}$

- периодограмма.

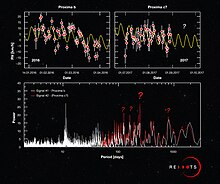Периодограмма для Проксимы Центавра b показана на внизу.

Когда периодограмма используется для изучения подробных характеристик КИХ-фильтра или оконной функции, параметр N выбирается так, чтобы он был кратен ненулевому значению. продолжительность последовательности x [n], которая называется заполнением нулями (см. § Выборка DTFT ). Когда он используется для реализации банка фильтров, N является несколькими частями ненулевой длительности последовательности x [n] (см. § Выборка DTFT ).

Одним из недостатков периодограммы является то, что дисперсия на заданной частоте не уменьшается по мере увеличения количества выборок, используемых в вычислениях. Он не обеспечивает усреднение, необходимое для анализа шумоподобных сигналов или даже синусоид при низких отношениях сигнал / шум. Оконные функции и импульсные характеристики фильтра не имеют шума, но для многих других сигналов требуются более сложные методы спектральной оценки. В двух альтернативных вариантах периодограммы используются как часть процесса:

• Метод усредненных периодограмм, более известный как метод Велча, делит длинную последовательность x [n] на несколько более коротких и, возможно, перекрывающихся, подпоследовательности. Он вычисляет оконную периодограмму каждого из них и вычисляет среднее значение массива, то есть массив, где каждый элемент является средним значением соответствующих элементов всех периодограмм. Для стационарных процессов это уменьшает дисперсию шума каждого элемента примерно на коэффициент, обратный количеству периодограмм.
• Сглаживание - это метод усреднения по частоте, а не по времени. Сглаженную периодограмму иногда называют спектральным графиком.

Методы, основанные на периодограммах, вносят небольшие смещения, которые неприемлемы в некоторых приложениях. Другие методы, которые не основываются на периодограммах, представлены в статье оценка спектральной плотности.

• Согласованный фильтр
• Отфильтрованная обратная проекция (преобразование Радона)
• Метод Велча
• Метод Бартлетта
• Дискретное преобразование Фурье
• Спектральный анализ методом наименьших квадратов анализ, для вычисления периодограмм в данных с неравномерным интервалом
• MUltiple SIgnal Classification (MUSIC), популярный параметрический метод сверхразрешения
• SAMV