Нелинейный фриктиофорез

Нелинейный фриктиофорез - это однонаправленный дрейф частицы в среде, вызванный периодической движущей силой с нулевым средним. Эффект возможен из-за нелинейной зависимости силы трения-сопротивления от скорости частицы. Он был открыт теоретически и известен в основном как нелинейный электрофриктиофорез. На первый взгляд, периодическая движущая сила с нулевым средним значением способна вовлечь частицу в колебательное движение без однонаправленного дрейфа, потому что интегральный импульс, передаваемый частице силой, равен нулю. Возможность однонаправленного дрейфа можно распознать, если учесть, что частица сама теряет импульс, передавая его дальше среде, в которой она движется. Если трение нелинейно, то может случиться так, что потеря количества движения при движении в одном направлении не будет равна потере импульса в противоположном направлении, и это вызовет однонаправленный дрейф. Чтобы это произошло, зависимость движущей силы от времени должна быть более сложной, чем в случае одной синусоидальной гармоники.

• 1 Простой пример - пластик Бингема
  • 1.1 Нелинейное трение
  • 1.2 Периодическая движущая сила
  • 1.3 Однонаправленный дрейф
• 2 Математический анализ
• 3 Приложения
  • 3.1 Разделение ДНК по длине
  • 3.2 Разделение по удельной массе
• 4 Удлинения
  • 4.1 Вращение с помощью круговой волны
  • 4.2 Модификация потенциальной функции
  • 4.3 Другая нелинейность
• 5 Ссылки

Нелинейное трение

Простейшим случаем зависимости трения от скорости является закон Стокса :

$(1)\; F\; dr\; (\; v)\; знак\; равно\; \lambda \; v,\; \{\backslash \; displaystyle\; (1)\; \backslash \; qquad\; F\_\; \{dr\}\; (v)\; =\; \backslash \; lambda\; v,\}$

где $F\; dr\; (v)\; \{\backslash \; displaystyle\; F\_\; \{dr\}\; (v)\}$- сила трения / сопротивления, приложенная к частице, движущейся со скоростью $v\; \{\backslash \; displaystyle\; v\}$в среде. Закон трения-скорости (1) наблюдается для медленно движущейся сферической частицы в ньютоновской жидкости.

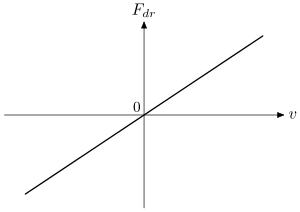
Рис. 1 Линейное трение

Оно линейное, см. Рис. 1, и не подходит для проведения нелинейного фриктиофореза. Характерным свойством закона (1) является то, что любая, даже очень небольшая движущая сила способна заставить частицу двигаться. Это не относится к таким материалам, как пластик Bingham. Для этих сред необходимо применить некоторую пороговую силу, $d\; \{\backslash \; displaystyle\; d\}$, чтобы заставить частицу двигаться. Этот вид закона трения-скорости (сухое трение) имеет скачкообразный разрыв в $v\; =\; 0\; \{\backslash \; displaystyle\; v\; =\; 0\}$:

$(2)\; F\; dr\; (v)\; =\; \lambda \; v\; +\; d\; \cdot \; sign\; (v).\; \{\backslash \; displaystyle\; (2)\; \backslash \; qquad\; F\_\; \{dr\}\; (v)\; =\; \backslash \; lambda\; v\; +\; d\; \backslash \; cdot\; \backslash \; mathrm\; \{sign\}\; (v).\}$

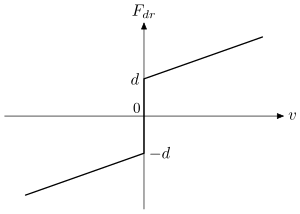
Рис. 2 Пример нелинейного трения

Он нелинейный, см. Рис. 2, и используется в этом примере.

Периодическая движущая сила

Пусть $T>0\; \{\backslash \; displaystyle\; T>0\}$обозначают период движущей силы. Выберите значение времени $t\; 1\; \{\backslash \; displaystyle\; t\_\; \{1\}\; \}$такой, что и два значения силы, $F\; +>0\; \{\backslash \; displaystyle\; F\; ^\; \{+\}>0\}$, таким образом, чтобы выполнялись следующие отношения :

$(3)\; F\; +\; t\; 1\; +\; F\; -\; (T\; -\; t\; 1)\; =\; 0.\; \{\backslash \; displaystyle\; (3)\; \backslash \; qquad\; F\; ^\; \{+\}\; t\_\; \{1\}\; +\; F\; ^\; \{-\}\; (T-t\_\; \{1\})\; =\; 0.\}$

Периодическая движущая сила $f\; (\; t)\; \{\backslash \; displaystyle\; f\; (t)\}$, используемый в этом примере, выглядит следующим образом:

Очевидно, что из-за to (3), $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$имеет нулевое среднее значение:

$\int \; 0\; T\; f\; (t)\; dt\; =\; F\; +\; t\; 1\; +\; F\; -\; (\; T\; -\; t\; 1)\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \backslash \; limits\; \_\; \{0\}\; ^\; \{T\}\; f\; (t)\; dt\; =\; F\; ^\; \{+\}\; t\_\; \{1\}\; +\; F\; ^\; \{-\}\; (T-t\_\; \{1\; \})\; =\; 0.\}$

Рис. 3 Пример с нулевой средней движущей силой

См. Также рис. 3.

Однонаправленный дрейф

Для простоты мы рассматриваем здесь физическую ситуацию, когда инерцией можно пренебречь. Последнее может быть достигнуто, если масса частицы мала, скорость мала и трение велико. Эти условия должны гарантировать, что $\tau \; \ll \; t\; 1\; \{\backslash \; displaystyle\; \backslash \; tau\; \backslash \; ll\; t\_\; \{1\}\}$, где $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$равно время релаксации. В этой ситуации частица, движущаяся силой (4), немедленно начинает двигаться с постоянной скоростью $v\; +\; =\; 1\; \lambda \; (F\; +\; -\; d)\; \{\backslash \; displaystyle\; v\; ^\; \{+\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\; \}\}\; (F\; ^\; \{+\}\; -\; d)\}$в течение интервала и немедленно прекратит движение в течение интервала , см. Рис. 4.

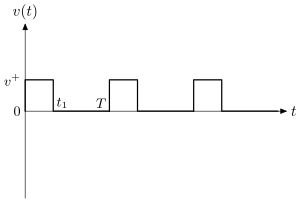
Рис. 4 Скорость с ненулевым средним

Это приводит к положительной средней скорости однонаправленного дрейфа:

$v\; (t)\; ¯\; =\; 1\; T\; \int \; 0\; T\; v\; (t)\; dt\; =\; t\; 1\; \lambda \; T\; (F\; +\; -\; d)>0.\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; \{\backslash \; overline\; \{v\; (t)\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash \; int\; \backslash \; limits\; \_\; \{0\}\; ^\; \{T\}\; v\; (t)\; dt\; =\; \{\backslash \; frac\; \{\; t\_\; \{1\}\}\; \{\backslash \; lambda\; T\}\}\; (F\; ^\; \{+\}\; -\; d)>0.\}$

Анализ возможности получения ненулевого дрейфа с помощью периодической силы было сделано в. Безразмерное уравнение движения частицы, движущейся под действием периодической силы $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$, $f\; (t\; +\; 1)\; =\; f\; (t)\; \{\backslash \; displaystyle\; f\; (\; t\; +\; 1)\; знак\; равно\; е\; (t)\}$, $\int \; 0\; 1\; f\; (t)\; dt\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; f\; (t)\; dt\; =\; 0\}$выглядит следующим образом:

$(5)\; v\; \dot{}\; +\; \lambda \; v\; -\; ϵ\; g\; (v)\; =\; f\; (t),\; \{\backslash \; displaystyle\; (5)\; \backslash \; qquad\; \{\backslash \; dot\; \{v\}\}\; +\; \backslash \; lambda\; v-\; \backslash \; epsilon\; g\; (v)\; =\; f\; (t),\}$

где сила трения / сопротивления $F\; dr\; (v)\; =\; \lambda \; v\; -\; ϵ\; g\; (v)\; \{\backslash \; displaystyle\; F\_\; \{dr\}\; (v)\; =\; \backslash \; lambda\; v\; -\; \backslash \; epsilon\; g\; (v)\}$удовлетворяет следующему:

$F\; dr\; (-\; v)\; =\; -\; F\; dr\; (v),\; ddv\; F\; dr\; (\; v)\; \ge \; 0.\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; F\_\; \{dr\}\; (-\; v)\; =\; -\; F\_\; \{dr\}\; (v),\; \backslash \; quad\; \{\backslash \; frac\; \{d\}\; \{dv\}\}\; F\_\; \{dr\}\; (v)\; \backslash \; geq\; 0.\}$

Доказано, что любое решение (5) переходит в периодический режим $v\; \ast \; (t)\; \{\backslash \; displaystyle\; v\; ^\; \{*\}\; (t)\}$, $v\; \ast \; (t\; +\; 1)\; =\; v\; \ast \; (t)\; \{\backslash \; displaystyle\; v\; ^\; \{*\}\; (t\; +\; 1)\; =\; v\; ^\; \{*\}\; (t)\}$, что имеет ненулевое среднее значение:

$v\; \ast \; (\; t)\; ¯\; знак\; равно\; \int \; 0\; 1\; v\; \ast \; (t)\; dt\; \ne \; 0,\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; \{\backslash \; overline\; \{v\; ^\; \{*\}\; (t)\}\}\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{0\}\; ^\; \{1\}\; v\; ^\; \{*\}\; (t)\; dt\; \backslash \; neq\; 0,\}$

почти наверняка при условии, что $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$не является антипериодическим.

Для $g\; (v)\; =\; v\; 3\; \{\backslash \; displaystyle\; g\; (v)\; =\; v\; ^\; \{3\}\}$, два случая $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$были учтены явно:

1. Пилообразная движущая сила, см. Рис. 5:

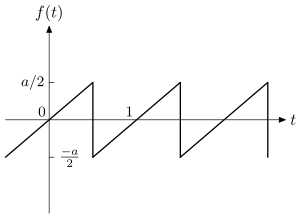
Рис. 5 Пилообразная движущая сила

$f\; (t)\; =\; a\; t,\; t\; \in \; [-\; 1/2;\; 1/2],\; f\; (t\; +\; 1)\; =\; f\; (t),\; t\; \in ]\; -\; \infty ;\; \infty \; [.\; \{\backslash \; Displaystyle\; \backslash \; qquad\; \backslash \; qquad\; е\; (т)\; =\; ат,\; \backslash \; четырехъядерный\; т\; \backslash \; в\; [-1/2;\; 1/2],\; \backslash \; четырехъядерный\; е\; (т\; +\; 1)\; =\; е\; (т),\; \backslash \; четырехъядерный\; т\; \backslash \; в]\; -\; \backslash \; infty;\; \backslash \; infty\; [.\}$

В данном случае найдено в первом порядке в приближении $ϵ\; \{\backslash \; displaystyle\; \backslash \; epsilon\}$к $v\; \ast \; (t)\; \{\backslash \; displaystyle\; v\; ^\; \{*\}\; (t)\}$, $v\; 1\; \ast \; (t)\; \{\backslash \; displaystyle\; v\_\; \{1\}\; ^\; \{*\}\; (t)\}$, имеет следующее среднее значение:

$|\; v\; 1\; \ast \; (t)\; ¯\; |\; \equiv \; |\; \int \; 0\; 1\; v\; 1\; \ast \; (t)\; d\; t\; |\; \ge \; 2\; 3\; ϵ\; а\; 3\; /\; \lambda \; 5.\; \{\backslash \; Displaystyle\; \backslash \; qquad\; \backslash \; qquad\; \{\backslash \; Big\; |\}\; \{\backslash \; overline\; \{v\_\; \{1\}\; ^\; \{*\}\; (t)\}\}\; \{\backslash \; Big\; |\}\; \backslash \; Equiv\; \{\backslash \; Big\; |\}\; \backslash \; int\; \backslash \; limits\; \_\; \{0\}\; ^\; \{1\}\; v\_\; \{1\}\; ^\; \{*\}\; (t)\; dt\; \{\backslash \; Big\; |\}\; \backslash \; geq\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; epsilon\; a\; ^\; \{3\}\; /\; \backslash \; lambda\; ^\; \{5\}.\}$

Эта оценка сделана с ожиданием $\lambda \; \gg \; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; \backslash \; gg\; 1\}$.

2. Движущая сила двух гармоник,

$f\; (t)\; =\; a\; cos\; \; (2\; \pi \; t)\; +\; b\; cos\; \; (4\; \pi \; t\; +\; \psi ).\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; f\; (t)\; =\; a\; \backslash \; cos\; (2\; \backslash \; pi\; t)\; +\; b\; \backslash \; cos\; (4\; \backslash \; pi\; t\; +\; \backslash \; psi).\}$

В этом случае первый порядок в $ϵ\; \{\backslash \; displaystyle\; \backslash \; epsilon\}$аппроксимация имеет следующее среднее значение:

$|\; v\; 1\; \ast \; (t)\; ¯\; |\; =\; |\; \int \; 0\; 1\; v\; 1\; \ast \; (t)\; d\; t\; |\; \ge \; 2\; 27\; ϵ\; \lambda \; (M\; \lambda )\; 3\; 1\; (1\; +\; 4\; \pi \; 2\; \lambda \; 2)\; (1\; +\; 16\; \pi \; 2\; \lambda \; 2)\; 1/2.\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; \{\backslash \; Big\; |\}\; \{\backslash \; overline\; \{v\_\; \{1\}\; ^\; \{*\}\; (t)\}\}\; \{\backslash \; Big\; |\}\; =\; \{\backslash \; Big\; |\}\; \backslash \; int\; \backslash \; limits\; \_\; \{0\}\; ^\; \{\; 1\}\; v\_\; \{1\}\; ^\; \{*\}\; (t)\; dt\; \{\backslash \; Big\; |\}\; \backslash \; geq\; \{\backslash \; frac\; \{2\}\; \{27\}\}\; \{\backslash \; frac\; \{\backslash \; epsilon\}\; \{\backslash \; lambda\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\; M\}\; \{\backslash \; lambda\}\}\; \backslash \; right)\; ^\; \{3\}\; \{\backslash \; frac\; \{1\}\; \{(1\; +\; \{\backslash \; frac\; \{4\; \backslash \; pi\; ^\; \{2\}\}\; \{\backslash \; lambda\; ^\; \{2\}\}\})\; (1+\; \{\; \backslash \; frac\; \{16\; \backslash \; pi\; ^\; \{2\}\}\; \{\backslash \; lambda\; ^\; \{2\}\}\})\; ^\; \{1/2\}\}\}.\}$

Это значение максимизируется в $\psi \; \{\backslash \; displaystyle\; \backslash \; psi\}$, $a,\; b\; \{\backslash \; displaystyle\; a,\; b\}$, сохраняя константу $a\; +\; b\; =\; M\; \{\backslash \; displaystyle\; a\; +\; b\; =\; M\}$. Интересно, что значение дрейфа зависит от $\psi \; \{\backslash \; displaystyle\; \backslash \; psi\}$и дважды меняет свое направление по мере того, как $\psi \; \{\backslash \; displaystyle\; \backslash \; psi\}$проходит в интервале $[0;\; 2\; \pi ]\; \{\backslash \; displaystyle\; [0;\; 2\; \backslash \; pi]\}$. Другой тип анализа, основанный на нарушении симметрии, также предполагает, что нулевое среднее значение движущей силы способно вызвать направленный дрейф.

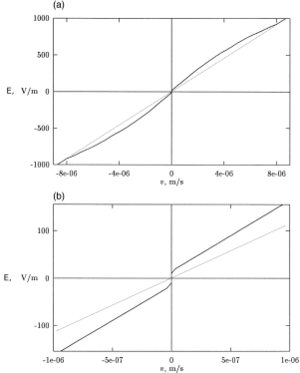
Рис.6 (а): сплошная линия - сила сопротивления на заряд на одиночном б.п. от скорости, пунктирная линия - линейная аппроксимация для сравнения. (b): то же, что и (a), но в мелком масштабе

В приложениях характер силы $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$в (5), обычно электрическая, подобно силам, действующим во время стандартного электрофореза. Единственное отличие состоит в том, что сила периодическая и без постоянной составляющей.

Чтобы эффект проявился, зависимость силы трения / сопротивления от скорости должна быть нелинейной. Так обстоит дело с многочисленными веществами, известными как неньютоновские жидкости. Среди них гели и дилатантные жидкости, псевдопластические жидкости, жидкие кристаллы. Специализированные эксперименты определили $F\; d\; r\; (v)\; \{\backslash \; displaystyle\; F\_\; \{dr\}\; (v)\}$для стандартной лестницы ДНК длиной до 1500 п.н. в 1,5% агарозном геле. Найденная зависимость, см. Рис. 6, подтверждает возможность нелинейного фриктиофореза в такой системе. На основе данных на рис. 6 был найден оптимальный временной ход для возбуждения электрического поля с нулевым средним, $E\; (t)\; \{\backslash \; displaystyle\; E\; (t)\}$, в котором обеспечивается максимальное дрейф на 1500 б.п. длинный фрагмент, см. рис. 7.

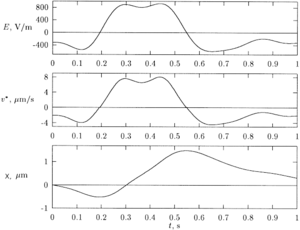
Рис. 7 Временной ход оптимального электрического поля, $E\; (t)\; \{\backslash \; displaystyle\; E\; (t)\}$, $E\; (t\; \pm \; 1\; s)\; =\; E\; (t)\; \{\backslash \; displaystyle\; E\; (t\; \backslash \; pm\; 1s)\; =\; E\; (t)\}$, установившаяся скорость, $v\; \ast \; (t)\; \{\backslash \; displaystyle\; v\; ^\; \{*\}\; (t)\}$, и смещение, $X\; (т)\; \{\backslash \; Displaystyle\; X\; (т)\}$. Значение сноса $v\; \ast \; (t)\; ¯\; =\; 0,31\; \mu \; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{v\; ^\; \{*\}\; (t)\}\}\; =\; 0,31\; \backslash \; mu\}$м / с.

Эффект однонаправленного дрейфа, вызванный периодической силой с нулевым интегральным значением, имеет своеобразную зависимость от времени действия приложенной силы. Примеры см. В предыдущем разделе. Это открывает новое измерение для ряда проблем разделения.

Разделение ДНК по длине

При разделении фрагментов ДНК в электрофорезе с нулевым интегральным полем (ZIFE) используется периодическое электрическое поле с нулевым средним периодом, где зависимость поля от времени аналогична показанный на рис. 3. Это позволяет разделять длинные фрагменты в агарозном геле, не разделяемые стандартным электрофорезом в постоянном поле. Длинная геометрия ДНК и способ ее движения в геле, известный как рептация, не позволяют напрямую применять соображения, основанные на уравнении. (5), выше.

Разделение по удельной массе

Было замечено, что при определенных физических условиях механизм, описанный в разделе «Математический анализ» выше, можно использовать для разделения по удельной массе, например, частицы изготовлены из изотопов того же материала.

Идея организации направленного дрейфа с периодическим возбуждением с нулевым средним получила дальнейшее развитие для других конфигураций и других физических механизмов нелинейности.

Вращение с помощью круговой волны

электрический диполь, свободно вращающийся вокруг $z\; \{\backslash \; displaystyle\; z\}$-оси в среде с нелинейным трением можно управлять, применяя электромагнитную волну, поляризованную по кругу вдоль $\pm \; z\; \{\backslash \; displaystyle\; \backslash \; pm\; z\}$и состоящую из двух гармоник. Уравнение движения для этой системы выглядит следующим образом:

$\omega \; \dot{}\; +\; \lambda \; \omega \; -\; ϵ\; g\; (\omega )\; =\; f\; (t,\; \theta \; (t)),\; \theta \; \dot{}\; =\; \omega ,\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; \{\backslash \; точка\; \{\backslash \; omega\}\}\; +\; \backslash \; lambda\; \backslash \; omega\; -\; \backslash \; epsilon\; g\; (\backslash \; omega)\; =\; f\; (t,\; \backslash \; theta\; (t)),\; \backslash \; quad\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; =\; \backslash \; omega,\}$

где $f\; (t,\; \theta \; (t))\; \{\backslash \; displaystyle\; f\; (t,\; \backslash \; theta\; (t))\}$- крутящий момент, действующий на диполь из-за круговой волны:

$(6)\; f\; (t,\; \theta \; (t))\; \sim \; |\; p\; |\; (A\; 1\; соз\; \; (\omega \; T\; \pm \; \theta )\; +\; A\; 2\; соз\; \; (2\; \omega \; T\; \pm \; \theta \; +\; \psi )),\; \{\backslash \; displaystyle\; (6)\; \backslash \; qquad\; f\; (t,\; \backslash \; theta\; (t))\; \backslash \; sim\; |\; p\; |\; (A\_\; \{1\}\; \backslash \; cos\; (\backslash \; omega\; t\; \backslash \; pm\; \backslash \; theta)\; +\; A\_\; \{2\}\; \backslash \; cos\; (2\; \backslash \; omega\; t\; \backslash \; pm\; \backslash \; theta\; +\; \backslash \; psi)),\}$

где $p\; \{\backslash \; displaystyle\; p\}$- составляющая дипольного момента, ортогональная оси $z\; \{\backslash \; displaystyle\; z\}$, а $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$определяет направление диполя в плоскости $XY\; \{\backslash \; displaystyle\; XY\}$. Выбрав правильный фазовый сдвиг $\psi \; \{\backslash \; displaystyle\; \backslash \; psi\}$в (6), можно ориентировать диполь в любом желаемом направлении, $\theta \; 0\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{0\; \}\}$. Направление $\theta \; 0\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{0\}\}$достигается за счет направленного углового дрейфа, который становится равным нулю, когда $\theta \; =\; \theta \; 0\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; \backslash \; theta\; \_\; \{0\}\}$. Небольшая расстройка между первой и второй гармониками в (6) приводит к непрерывному вращательному дрейфу.

Модификация потенциальной функции

Рис. 8 Пример модификации потенциальной функции $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$из-за нелинейного фриктиофореза. (a) начальный $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$, (b) модифицированный $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$.

Если a частица совершает направленный дрейф при свободном перемещении в соответствии с формулой. (5), то он дрейфует аналогично, если наложено достаточно мелкое потенциальное поле $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$. Уравнение движения в этом случае:

$v\; \dot{}\; +\; \lambda \; v\; -\; ϵ\; g\; (v)\; =\; f\; (t)\; -\; \varphi \; (x),\; x\; \dot{}\; =\; v,\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; \{\backslash \; dot\; \{v)\; \}\}\; +\; \backslash \; lambda\; v-\; \backslash \; epsilon\; g\; (v)\; =\; f\; (t)\; -\; \backslash \; phi\; (x),\; \backslash \; quad\; \{\backslash \; dot\; \{x\}\}\; =\; v,\}$

где $\varphi \; (x)\; \{\; \backslash \; displaystyle\; \backslash \; phi\; (x)\}$- сила, создаваемая потенциальным полем. Дрейф продолжается до тех пор, пока не будет достигнута достаточно крутая область в течение $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$, которая может остановить дрейф. Такое поведение, как показывает строгий математический анализ, приводит к модификации $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$путем добавления линейного в $x\; \{\backslash \; displaystyle\; x\}$срок. Это может изменить $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$качественно, например, изменение количества точек равновесия, см. рис. 8. Эффект может быть существенным при воздействии высокочастотного электрического поля на биополимеры.

Другая нелинейность

Для электрофореза коллоидных частиц в электрическом поле малой напряженности сила $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$в правой части уравнения. (5) линейно пропорциональна прочности $E\; (t)\; \{\backslash \; displaystyle\; E\; (t)\}$приложенного электрического поля. При высокой прочности линейность нарушается из-за нелинейной поляризации. В результате сила может нелинейно зависеть от приложенного поля:

$f\; (t)\; \sim \; E\; (t)\; +\; \alpha \; (E\; (t))\; 3.\; \{\backslash \; displaystyle\; \backslash \; qquad\; \backslash \; qquad\; f\; (t)\; \backslash \; sim\; E\; (t)\; +\; \backslash \; alpha\; (E\; (t))\; ^\; \{3\}.\}$

В последнем выражении, даже если примененное поле, $E\; (t)\; \{\backslash \; displaystyle\; E\; (t)\}$имеет нулевое среднее значение, приложенная сила $f\; (t)\; \{\backslash \; displaystyle\; f\; (t)\}$может иметь постоянная составляющая, которая может вызвать направленный дрейф. Как и выше, для этого $E\; (t)\; \{\backslash \; displaystyle\; E\; (t)\}$должен иметь более одной синусоидальной гармоники. Такой же эффект для жидкости в трубке может использоваться в электроосмотическом насосе, приводимом в действие с нулевым средним электрическим полем.