Парадокс Линдли

Парадокс Линдлите в этом противоречащий ситуация в статистике, в которых байесовские и частотных подходы к проверке гипотез проблем дают различные результаты для некоторых вариантов в априорном распределении. Проблема разногласий между двумя подходами обсуждалась в учебнике Гарольда Джеффриса 1939 года; он стал известен как парадокс Линдли после того, как Деннис Линдли назвал разногласие парадоксом в статье 1957 года.

Хотя это и называется парадоксом, разные результаты байесовского и частотного подходов можно объяснить их использованием для ответа на принципиально разные вопросы, а не фактического несогласия между двумя методами.

Тем не менее, для большого класса априорных подходов различия между частотным и байесовским подходами вызваны сохранением фиксированного уровня значимости: как признавал даже Линдли, «теория не оправдывает практику сохранения фиксированного уровня значимости» и даже «некоторые расчеты профессора Пирсона в обсуждении этой статьи подчеркнули, как уровень значимости должен измениться с размером выборки, если бы потери и априорные вероятности оставались фиксированными ''. Фактически, если критическое значение увеличивается с увеличением размера выборки соответствующим образом быстро, то расхождение между частотным и байесовским подходами становится незначительным по мере увеличения размера выборки.

• 1 Описание парадокса
• 2 Числовой пример
  • 2.1 Частотный подход
  • 2.2 Байесовский подход
  • 2.3 Согласование байесовского и частотного подходов
  • 2.4 Отсутствие реального парадокса
• 3 Недавнее обсуждение
• 4 См. Также
• 5 Примечания
• 6 Дальнейшее чтение

Результат некоторого эксперимента имеет два возможных объяснения, гипотезы и некоторое предварительное распределение, представляющее неопределенность в отношении того, какая гипотеза более точна, прежде чем принимать во внимание. ${\ displaystyle \ textstyle x}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$${\ displaystyle \ textstyle \ pi}$${\ displaystyle \ textstyle x}$

Парадокс Линдли возникает, когда

1. Результат является «значимым» с помощью частотного теста, указывающего на достаточные доказательства для отклонения, скажем, на уровне 5%, и${\ displaystyle \ textstyle x}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {0}}$
2. Апостериорная вероятность на данный высока, что указывает на убедительные доказательства того, что лучше согласуется с чем.${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle x}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle x}$${\ displaystyle \ textstyle H_ {1}}$

Эти результаты могут быть получены в то же самое время, когда они очень специфичны, более размыты, а предварительное распределение не сильно благоприятствует тому или иному, как показано ниже. ${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$

Следующий числовой пример иллюстрирует парадокс Линдли. В одном городе за определенный период времени родился 49 581 мальчик и 48 870 девочек. Таким образом, наблюдаемая доля рождений мужского пола составляет 49 581/98 451 ≈ 0,5036. Мы предполагаем, что доля рождений мужского пола является биномиальной переменной с параметром. Мы заинтересованы в том, чтобы проверить, равно ли 0,5 или какое-то другое значение. То есть наша нулевая гипотеза есть, а альтернатива есть. ${\ displaystyle \ textstyle x}$ ${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle H_ {0}: \ theta = 0,5}$${\ displaystyle \ textstyle H_ {1}: \ theta \ neq 0,5}$

Частотный подход

Частотный подход к тестированию состоит в том, чтобы вычислить p-значение, то есть вероятность наблюдения доли мальчиков, по крайней мере, столь же велика, как и предположение. Поскольку число рождений очень велико, мы можем использовать нормальное приближение доли рождений мужского пола с и, чтобы вычислить ${\ displaystyle \ textstyle H_ {0}}$ ${\ displaystyle \ textstyle x}$${\ displaystyle \ textstyle H_ {0}}$ ${\ displaystyle \ textstyle X \ sim N (\ mu, \ sigma ^ {2})}$${\ displaystyle \ textstyle \ mu = np = n \ theta = 98 451 \ times 0,5 = 49 225,5}$${\ displaystyle \ textstyle \ sigma ^ {2} = n \ theta (1- \ theta) = 98 451 \ times 0,5 \ times 0,5 = 24 612,75}$

${\ Displaystyle {\ begin {align} P (X \ geq x \ mid \ mu = 49225.5) = \ int _ {x = 49581} ^ {98451} {\ frac {1} {\ sqrt {2 \ pi \ sigma ^ {2}}}} e ^ {- ({\ frac {u- \ mu} {\ sigma}}) ^ {2} / 2} du \\ = \ int _ {x = 49581} ^ {98451} {\ frac {1} {\ sqrt {2 \ pi (24 612,75)}}} e ^ {- {\ frac {(u-49225.5) ^ {2}} {24612.75}} / 2} du \ приблизительно 0,0117. \ конец {выровнен}}}$

Мы были бы в равной степени удивлены, если бы увидели 49 581 женское рождение, т. Е. Поэтому частотный специалист обычно проводил бы двусторонний тест, для которого значение p было бы равным. В обоих случаях значение p ниже уровня значимости α, равного 5%, поэтому частотный подход отвергает, поскольку он не согласуется с наблюдаемыми данными. ${\ displaystyle \ textstyle x \ приблизительно 0,4964}$ ${\ displaystyle \ textstyle p \ примерно 2 \ раза 0,0117 = 0,0235}$${\ displaystyle \ textstyle H_ {0}}$

Байесовский подход

При отсутствии причин отдавать предпочтение одной гипотезе над другой, байесовский подход заключался бы в том, чтобы присвоить априорные вероятности и равномерное распределение меньшим, а затем вычислить апостериорную вероятность использования теоремы Байеса, ${\ displaystyle \ textstyle \ pi (H_ {0}) = \ pi (H_ {1}) = 0,5}$${\ displaystyle \ textstyle \ theta}$${\ displaystyle H_ {1}}$${\ displaystyle \ textstyle H_ {0}}$

${\ Displaystyle P (H_ {0} \ mid k) = {\ frac {P (k \ mid H_ {0}) \ pi (H_ {0})} {P (k \ mid H_ {0}) \ pi (H_ {0}) + P (k \ mid H_ {1}) \ pi (H_ {1})}}.}.$

После наблюдения за не рожденными мальчиками мы можем вычислить апостериорную вероятность каждой гипотезы, используя функцию массы вероятности для биномиальной переменной, ${\ displaystyle \ textstyle k = 49 581}$${\ displaystyle \ textstyle n = 98 451}$

${\ displaystyle {\ begin {align} P (k \ mid H_ {0}) amp; = {n \ choose k} (0,5) ^ {k} (1-0,5) ^ {nk} \ приблизительно 1,95 \ times 10 ^ {-4} \\ P (k \ mid H_ {1}) amp; = \ int _ {0} ^ {1} {n \ choose k} \ theta ^ {k} (1- \ theta) ^ {nk} d \ theta = {n \ choose k} \ mathrm {\ mathrm {B}} (k + 1, n-k + 1) = 1 / (n + 1) \ приблизительно 1,02 \ times 10 ^ {- 5} \ конец {выровнен}}}$

где - бета-функция. ${\ Displaystyle \ textstyle \ mathrm {\ mathrm {B}} (а, б)}$

Из этих значений мы находим апостериорную вероятность, которая в значительной степени превышает. ${\ Displaystyle P (\ textstyle H_ {0} \ mid k) \ приблизительно 0,95}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$

Два подхода - байесовский и частотный - кажутся конфликтующими, и в этом заключается «парадокс».

Согласование байесовского и частотного подходов

Однако, по крайней мере, в примере Линдли, если мы возьмем последовательность уровней значимости α n, такую, что α n = n ^{- r} с r gt; 1/2, тогда апостериорная вероятность нуля сходится к 0, что согласуется с отказ от нуля. В этом числовом примере принятие r = 1/2 дает уровень значимости 0,00318, поэтому частотный специалист не отвергнет нулевую гипотезу, что примерно соответствует байесовскому подходу.

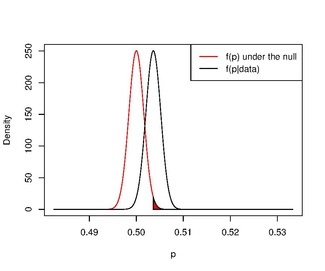Распределение p при нулевой гипотезе и апостериорное распределение p.

Если мы воспользуемся малоинформативным априором и проверим гипотезу, более похожую на гипотезу частотного подхода, парадокс исчезнет.

Например, если мы вычисляем апостериорное распределение, используя однородное априорное распределение на (т.е.), мы находим ${\ Displaystyle \ textstyle Р (\ тета \ середина х, п)}$${\ displaystyle \ textstyle \ theta}$${\ Displaystyle \ TextStyle \ пи (\ тета \ в [0,1]) = 1}$

${\ Displaystyle P (\ theta \ mid k, n) = \ mathrm {\ mathrm {B}} (k + 1, n-k + 1).}$

Если мы используем это, чтобы проверить вероятность того, что новорожденный, скорее всего, будет мальчиком, чем девочкой, т. Е. Мы найдем ${\ Displaystyle Р (\ тетаgt; 0,5 \ середина к, п)}$

${\displaystyle \int _{0.5}^{1}\mathrm {\mathrm {B} } (49582,48871)\approx 0.983.}$

Другими словами, очень вероятно, что доля рождений мужского пола выше 0,5.

Ни один из этих анализов не дает непосредственной оценки величины эффекта, но оба могут использоваться для определения, например, того, будет ли доля рождений мальчиков выше определенного порогового значения.

Отсутствие настоящего парадокса

Очевидное расхождение между двумя подходами вызвано сочетанием факторов. Во-первых, частотный подход, описанный выше, проверяет без ссылки на. Байесовский подход оценивается как альтернатива и обнаруживает, что первый лучше согласуется с наблюдениями. Это связано с тем, что последняя гипотеза гораздо более расплывчата, чем может быть где угодно, что приводит к тому, что она имеет очень низкую апостериорную вероятность. Чтобы понять, почему, полезно рассмотреть две гипотезы как генераторы наблюдений: ${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle [0,1]}$

• Под, мы выбираем, и спросить, насколько вероятно, чтобы увидеть 49,581 мальчиков в 98,451 родов.${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle \ theta \ приблизительно 0,500}$
• Ниже мы выбираем случайным образом от 0 до 1 и задаем тот же вопрос.${\ displaystyle \ textstyle H_ {1}}$${\ displaystyle \ textstyle \ theta}$

Большинство возможных значений для under очень плохо подтверждено наблюдениями. По сути, очевидное несогласие между методами - это вовсе не разногласия, а, скорее, два разных утверждения о том, как гипотезы соотносятся с данными: ${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle H_ {1}}$

• Частотный специалист считает, что это плохое объяснение наблюдения.${\ displaystyle \ textstyle H_ {0}}$
• Байесовские находки являются гораздо лучшим объяснением наблюдения, чем.${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$

Согласно частотному тесту, соотношение полов новорожденных невероятно 50/50. Тем не менее, 50/50 - лучшее приближение, чем большинство, но не все другие соотношения. Гипотеза подошла бы к наблюдению намного лучше, чем почти все другие соотношения, в том числе. ${\ displaystyle \ textstyle \ theta \ приблизительно 0,504}$${\ displaystyle \ textstyle \ theta \ приблизительно 0,500}$

Например, этот выбор гипотез и априорных вероятностей подразумевает утверждение: «если gt; 0,49 и lt;0,51, то априорная вероятность быть точно 0,5 составляет 0,50 / 0,51 98%». Учитывая такое сильное предпочтение, то легко понять, почему байесовский подход способствует в лице, даже если наблюдаемое значение лежит далеко от 0,5. Отклонение более чем на 2 сигмы от считается значительным в частотном подходе, но его значение отвергается предшествующим в байесовском подходе. ${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ theta}$${\ Displaystyle \ приблизительно}$${\ displaystyle \ theta = 0,5}$${\ displaystyle H_ {0}}$${\ displaystyle x \ приблизительно 0,5036}$${\ displaystyle x}$${\ displaystyle 2.28 \ sigma}$${\ displaystyle H_ {0}}$

Посмотрев на это с другой стороны, мы можем увидеть, что априорное распределение по существу является плоским с дельта-функцией на. Ясно, что это сомнительно. Фактически, если бы вы представили действительные числа как непрерывные, то было бы более логичным предположить, что никакое данное число не может быть точным значением параметра, т. Е. Мы должны предполагать. ${\ displaystyle \ textstyle \ theta = 0,5}$${\ Displaystyle P (\ theta = 0,5) = 0}$

Более реалистичное распределение для в альтернативной гипотезе дает менее удивительный результат для апостериорной части. Например, если мы заменим на, т. Е. Оценку максимального правдоподобия для, апостериорная вероятность будет только 0,07 по сравнению с 0,93 для (Конечно, на самом деле нельзя использовать MLE как часть априорного распределения). ${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {1}}$${\ displaystyle \ textstyle H_ {2}: \ theta = x}$ ${\ displaystyle \ textstyle \ theta}$${\ displaystyle \ textstyle H_ {0}}$${\ displaystyle \ textstyle H_ {2}}$

Парадокс продолжает оставаться предметом активной дискуссии.

• Байесовский фактор

• Шафер, Гленн (1982). «Парадокс Линдли». Журнал Американской статистической ассоциации. 77 (378): 325–334. DOI : 10.2307 / 2287244. JSTOR   2287244. Руководство по ремонту   0664677.