Рамочная диаграмма

редактировать

Визуализация данных

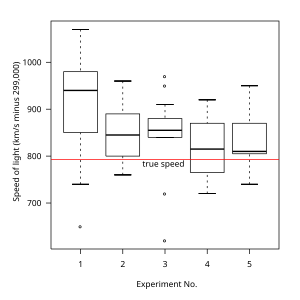
Рис. 1. Рамочная диаграмма данных из эксперимента Майкельсона – Морли

In описательная статистика, прямоугольная диаграмма или прямоугольная диаграмма - это метод графического изображения групп числовых данных через их квартили. Коробчатые диаграммы также могут иметь линии, идущие от прямоугольников (усов), указывающие на изменчивость за пределами верхнего и нижнего квартилей, отсюда термины диаграмма прямоугольник и усы и диаграмма прямоугольник и усы . Выбросы могут быть нанесены на график как отдельные точки. Коробчатые диаграммы непараметрически : они отображают вариации в выборках из статистической совокупности без каких-либо предположений о лежащем в основе статистическом распределении (хотя прямоугольная диаграмма Тьюки предполагает симметрию для усы и нормальность для их длины). Интервалы между различными частями поля указывают степень дисперсии (разброс) и асимметрии в данных и показывают выбросы. Помимо самих точек, они позволяют визуально оценивать различные L-оценки, в частности, межквартильный размах, midhinge, range, средний и трехсредний. Коробчатые диаграммы можно рисовать как по горизонтали, так и по вертикали. Бокс-диаграммы получили свое название от прямоугольника посередине.

Содержание

1 История прямоугольной диаграммы
2 Элементы прямоугольной диаграммы
3 Варианты
4 Пример (ы)
- 4.1 Пример без выбросов
- 4.2 Пример с выбросами
- 4.3 В случае больших наборов данных
  - 4.3.1 Общее уравнение для вычисления эмпирических квантилей
5 Визуализация
6 См. Также
7 Ссылки
8 Дополнительная литература
9 Внешние ссылки

История прямоугольной диаграммы

Полоса диапазона была введена Мэри Элеонор Спир в 1952 году и снова в 1969 году. Диаграмма с прямоугольником и усами была впервые представлена в 1970 году Джон Тьюки, который позже опубликовал эту тему в 1977 году.

Элементы прямоугольной диаграммы

Рисунок 2. Ящичковая диаграмма с усами от минимума до максимума

Рисунок 3. Та же прямоугольная диаграмма с усами с максимум 1,5 IQR

Коробчатая диаграмма - это стандартизованный способ отображения набора данных на основе сводки из пяти чисел : минимум, максимум, медиана выборки, а также первый и третий квартили.

Минимум : самая низкая точка данных без каких-либо выбросов.

Максимум : наибольшая точка данных без каких-либо выбросов.

Медиана (Q 2 / 50-й процентиль) : среднее значение набора данных.

Первый квартиль (Q 1 / 25-й процентиль) : также известный как нижний квартиль q n (0,25), это медиана нижней половины набора данных.

Третий квартиль (Q 3 / 75-й процентиль) : также известный как верхний квартиль q n (0,75), это медиана верхней половины набора данных..

Важным элементом, используемым для построения прямоугольной диаграммы путем определения минимальных и максимальных возможных значений данных, но не являющимся частью вышеупомянутой пятизначной сводки, является межквартильный диапазон или IQR, обозначенный ниже:

Межквартильный размах (IQR) : расстояние между верхним и нижним квартилями.

IQR = Q 3 - Q 1 = qn (0,75) - qn (0,25) {\ displaystyle {\ text {IQR}} = Q_ {3} -Q_ {1} = q_ {n} (0,75) -q_ {n} (0.25)}

{\ displaystyle {\ text {IQR}} = Q_ {3} -Q_ {1} = q_ {n} (0,75) -q_ {n} ( 0.25)}

Коробчатая диаграмма состоит из двух частей, прямоугольника и набора усов, показанных на рисунке 2. Самая низкая точка - это минимум набора данных, а самая высокая точка - максимум данных. задавать. Блок нарисован от Q 1 до Q 3 с горизонтальной линией, проведенной посередине для обозначения медианы.

Тот же набор данных также может быть представлен в виде прямоугольной диаграммы, показанной на рис. 3. Сверху верхнего квартиля измеряется расстояние, в 1,5 раза превышающее IQR, и проводится усы до самой большой наблюдаемой точки от набор данных, попадающий в это расстояние. Точно так же расстояние, в 1,5 раза превышающее IQR, измеряется ниже нижнего квартиля, а усы протягиваются до нижней наблюдаемой точки из набора данных, которая попадает в это расстояние. Все остальные наблюдаемые точки отображаются как выбросы.

Однако усы могут представлять несколько возможных альтернативных значений, среди которых:

минимум и максимум всех данных (как на рисунке 2)
одно стандартное отклонение выше и ниже среднего значения данных
9-го процентиля и 91-го процентиля
2-го процентиль и 98-й процентиль.

Любые данные, не включенные между усами, должны быть нанесены как выброс с точкой, маленьким кружком или звездочкой, но иногда это не делается.

Некоторые коробчатые диаграммы включают дополнительный символ для представления среднего значения данных.

На некоторых коробчатых диаграммах штриховка помещается на каждом усе перед концом уса.

В редких случаях коробчатые диаграммы могут быть представлены вообще без усов.

Из-за этой изменчивости уместно описать соглашение, используемое для усов и выбросов в заголовке графика.

Необычные процентили 2%, 9%, 91%, 98% иногда используются для штриховки усов и концов усов, чтобы показать семизначную сводку. Если данные нормально распределены, положения семи отметок на прямоугольной диаграмме будут равномерно распределены.

Варианты

Рис. 4. Четыре прямоугольных диаграммы, с выемками и без них, с переменной шириной

Поскольку математик Джон У. Тьюки популяризировал этот тип отображения визуальных данных в 1969 году, были описаны несколько вариаций традиционной коробчатой диаграммы. Двумя наиболее распространенными являются прямоугольные диаграммы переменной ширины и прямоугольные диаграммы с надрезом (см. Рисунок 4).

Ящичковые диаграммы переменной ширины иллюстрируют размер каждой группы, данные которой выводятся на график, делая ширину ящика пропорциональной размеру группы. Популярное соглашение состоит в том, чтобы сделать ширину прямоугольника пропорциональной квадратному корню из размера группы.

Графики прямоугольных сечений применяют «выемку» или сужение прямоугольника вокруг медианы. Вырезы полезны, поскольку предлагают приблизительное представление о значении разницы медиан; если выемки двух прямоугольников не перекрываются, это свидетельствует о статистически значимой разнице между медианами. Ширина меток пропорциональна межквартильному размаху (IQR) выборки и обратно пропорциональна квадратному корню из размера выборки. Однако существует неопределенность относительно наиболее подходящего множителя (так как он может варьироваться в зависимости от схожести дисперсий выборок). Одно соглашение заключается в использовании $± 1,58 IQR n {\ displaystyle \ pm {\ frac {1.58 {\ text {IQR}}} {\ sqrt {n}}}}$ ${\ displaystyle \ pm {\ frac {1.58 {\ text {IQR}}} { \ sqrt {n}}}}$ .

Скорректированные прямоугольные диаграммы предназначены для асимметричные распределения. Они полагаются на статистику асимметрии medcouple. Для среднего значения MC длины верхних и нижних усов соответственно определены как

1,5 IQR e 3 MC, 1,5 IQR ⋅ e - 4 MC, если MC ≥ 0, 1,5 IQR ⋅ e 4 MC, 1,5 IQR ⋅ e - 3 MC, если MC ≤ 0. {\ displaystyle {\ begin {matrix} 1.5 {\ text {IQR}} \ cdot e ^ {3 {\ text {MC}}}, 1.5 {\ text { IQR}} \ cdot e ^ {- 4 {\ text {MC}}} {\ text {if}} {\ text {MC}} \ geq 0, \\ 1.5 {\ text {IQR}} \ cdot e ^ {4 {\ text {MC}}}, 1.5 {\ text {IQR}} \ cdot e ^ {- 3 {\ text {MC}}} {\ text {if}} {\ text {MC}} \ leq 0. \ end {matrix}}}

{\ displaystyle {\ begin {matrix} 1.5 {\ text {IQR}} \ cdot e ^ {3 {\ text {MC}}}, 1.5 {\ text {IQR}} \ cdot e ^ {- 4 {\ text {MC}}} {\ text {if}} {\ text {MC}} \ geq 0, \\ 1.5 {\ text {IQR}} \ cdot e ^ {4 {\ text {MC}}}, 1.5 {\ text {IQR}} \ cdot e ^ {- 3 {\ text {MC}}} {\ text {if}} {\ text {MC}} \ leq 0. \ end {matrix}}}

Для симметричных распределений медпара будет равна нулю, и это сокращается до коробчатой диаграммы Тьюки с равными длинами усов $1,5 IQR {\ displaystyle 1.5 {\ text {IQR} }}$ ${\ displaystyle 1.5 {\ text {IQR}}}$ для обоих усов.

Другие виды графиков, такие как графики скрипки и bean-графики, могут показать разницу между одномодальным и мультимодальным распределениями, разницу, которую невозможно увидеть с исходным boxplot.

Пример (-ы)

Пример без выбросов

Рисунок 5. Сгенерированный рисунок прямоугольной диаграммы для нашего примера слева без выбросов.

Ряд почасовых температур был измеряется в течение дня в градусах Фаренгейта. Записанные значения перечислены в следующем порядке: 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.

Ящичковая диаграмма данных может быть сгенерирована путем вычисления пяти соответствующих значений: минимума, максимума, медианы, первого квартиля и третьего квартиля.

Минимум - это наименьший номер набора. В этом случае минимальная дневная температура составляет 57 ° F.

Максимум - это наибольшее число набора. В этом случае максимальная дневная температура составляет 81 ° F.

Медиана - это «средний» номер упорядоченного набора. Это означает, что ровно 50% элементов меньше медианы и 50% элементов больше медианы. Медиана этого заказанного набора составляет 70 ° F.

Значение первого квартиля - это число, которое отмечает одну четверть упорядоченного набора. Другими словами, ровно 25% элементов меньше первого квартиля и ровно 75% элементов больше. Значение первого квартиля можно легко определить, найдя «среднее» число между минимумом и медианой. Для почасовой температуры "среднее" число между 57 ° F и 70 ° F составляет 66 ° F.

Значение третьего квартиля - это число, обозначающее три четверти упорядоченного набора. Другими словами, ровно 75% элементов меньше первого квартиля и 25% элементов больше. Значение третьего квартиля можно легко определить, найдя «среднее» число между медианой и максимумом. Для почасовой температуры "среднее" число между 70 ° F и 81 ° F составляет 75 ° F.

Межквартильный размах, или IQR, можно вычислить:

IQR = Q 3 - Q 1 = 75 F - 66 ∘ F = 9 ∘ F. {\ displaystyle {\ text {IQR}} = Q_ {3} -Q_ {1} = 75 ^ {\ circ} F-66 ^ {\ circ} F = 9 ^ {\ circ} F.}

{\ displaystyle {\ text {IQR}} = Q_ {3} -Q_ {1} = 75 ^ {\ circ} F-66 ^ {\ circ} F = 9 ^ {\ circ} F.}

Следовательно, $1,5 IQR = 1,5 9 F = 13,5 F. {\ displaystyle 1,5 {\ text {IQR}} = 1,5 \ cdot 9 ^ {\ circ} F = 13,5 ^ {\ circ} F.}$ ${\ displaystyle 1.5 {\ text {IQR}} = 1.5 \ cdot 9 ^ {\ circ} F = 13,5 ^ {\ circ} F.}$

1,5 IQR выше третьего квартиля:

Q 3 + 1,5 IQR = 75 F + 13,5 F = 88,5 F. {\ displaystyle Q3 + 1.5 {\ text {IQR}} = 75 ^ {\ circ} F + 13.5 ^ {\ circ} F = 88.5 ^ {\ circ} F.}

{\ displaystyle Q3 + 1.5 {\ text {IQR}} = 75 ^ {\ circ} F + 13,5 ^ {\ circ} F = 88,5 ^ {\ circ} F.}

1.5IQR ниже первого квартиля:

Q 1 - 1,5 IQR = 66 F - 13,5 F = 52,5 F. {\ displaystyle Q_ {1} -1,5 {\ text {IQR}} = 66 ^ {\ circ} F-13,5 ^ {\ circ} F = 52,5 ^ {\ circ} F.}

{\ displaystyle Q_ {1} -1,5 {\ text {IQR}} = 66 ^ {\ circ} F-13,5 ^ {\ circ} F = 52,5 ^ {\ circ} F.}

Верхний ус Ящичковая диаграмма - это наибольший номер набора данных, меньший 1,5IQR выше третьего квартиля. Здесь 1,5IQR выше третьего квартиля составляет 88,5 ° F, а максимальное - 81 ° F. Следовательно, верхний ус нарисован на максимальном значении 81 ° F.

Точно так же нижний ус на прямоугольной диаграмме - это наименьший номер набора данных, превышающий 1,5IQR ниже первого квартиля. Здесь 1,5IQR ниже первого квартиля составляет 52,5 ° F, а минимальное - 57 ° F. Таким образом, нижний ус нарисован при минимальном значении 57 ° F.

Пример с выбросами

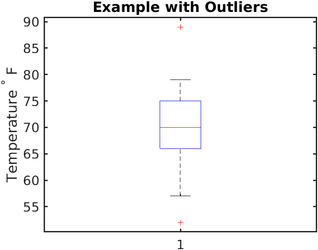Рисунок 6. Сгенерированная коробчатая диаграмма нашего примера слева с выбросами.

Выше приведен пример без выбросов. Вот следующий пример с выбросами:

Упорядоченный набор: 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.

В этом примере изменяются только первый и последний номер. Медиана, третий квартиль и первый квартиль остаются прежними.

В этом случае максимальное значение составляет 89 ° F, а 1,5IQR выше третьего квартиля составляет 88,5 ° F. Максимальное значение превышает 1,5IQR плюс третий квартиль, поэтому максимальное значение является выбросом. Следовательно, верхний ус нарисован с максимальным значением, меньшим, чем 1,5IQR, над третьим квартилем, который составляет 79 ° F.

Точно так же минимум 52 ° F и 1,5IQR ниже первого квартиля составляет 52,5 ° F. Минимальное значение меньше 1,5IQR минус первый квартиль, поэтому минимум также является выбросом. Следовательно, нижние усы отображаются при наименьшем значении, превышающем 1,5IQR, ниже первого квартиля, который составляет 57 ° F.

В случае больших наборов данных

Общее уравнение для вычисления эмпирических квантилей

qn (p) = x (k) + α (x (k + 1) - x (k)) {\ displaystyle q_ {n} (p) = x _ {(k)} + \ alpha (x _ {(k + 1)} - x _ {(k)})}

{\ displaystyle q_ {n} (p) = x _ {(k)} + \ альфа (х _ {(к + 1)} - х _ {(к)})}

с k = [p (n + 1)] и α = p (n + 1) - k {\ displaystyle {\ text {with}} k = [p (n + 1)] {\ text {and}} \ alpha = p (n + 1) -k}

{ \ displaystyle {\ text {with}} k = [p (n + 1)] {\ text {and}} \ alpha = p (n + 1) -k}

Используя приведенный выше пример с 24 точками данных, что означает n = 24, можно также вычислить медианное значение, первый и третий квартили математически и визуально.

Медиана : $qn (0,5) = q (12) + (0,5 25–12) ⋅ (x (13) - x (12)) = 70 + (0,5 ⋅ 25–12) ⋅ (70–70) = 70 {\ displaystyle q_ {n} (0,5) = q _ {(12)} + (0,5 \ cdot 25-12) \ cdot (x _ {(13)} - x _ {(12)}) = 70 + (0,5 \ cdot 25-12) \ cdot (70-70) = 70}$ ${\ displaystyle q_ {n} (0,5) = q _ {(12)} + (0,5 \ cdot 25-12) \ cdot (x _ {(13)} - x _ {(12)}) = 70+ (0,5 \ cdot 25-12) \ cdot (70-70) = 70}$

Первый квартиль : $qn (0,25) = q (6) + (0,25 ⋅ 25-6) ⋅ (Икс (7) - Икс (6)) = 66 + (0,25 ⋅ 25 - 6) ⋅ (66 - 66) = 66 {\ Displaystyle q_ {n} (0,25) = q _ {(6)} + ( 0,25 \ cdot 25-6) \ cdot (x _ {(7)} - x _ {(6)}) = 66+ (0,25 \ cdot 25-6) \ cdot (66-66) = 66}$ ${\ displaystyle q_ {n } (0,25) = q _ {(6)} + (0,25 \ cdot 25-6) \ cdot (x _ {(7)} - x _ {(6)}) = 66+ (0,25 \ cdot 25-6) \ cdot (66-66) = 66}$

Третий квартиль : $qn (0,75) = q (18) + (0,75 ⋅ 25 - 18) ⋅ (x (19) - x (18)) = 75 + (0,75 ⋅ 25 - 18) ⋅ (75 - 75) = 75 {\ displaystyle q_ {n} (0,75) = q _ {(18)} + (0,75 \ cdot 25-18) \ cdot (x _ {(19)} - x _ {(18)}) = 75+ (0,75 \ cdot 25-18) \ cdot (75-75) = 75}$ ${\ displaystyle q_ {n} (0,75) = q _ {(18)} + (0,75 \ cdot 25-18) \ cdot (x _ {(19)} - x _ {(18)}) = 75+ (0,75 \ cdot 25-18) \ cdot ( 75–75) = 75}$

Визуализация

Рис. 7. Ящичковая диаграмма и функция плотности вероятности (pdf) нормального N (0, 1σ) Население

Ящичковая диаграмма позволяет быстро графически исследовать один или несколько наборов данных. Ящичные диаграммы могут показаться более примитивными, чем гистограмма или оценка плотности ядра, но у них есть некоторые преимущества. Они занимают меньше места и поэтому особенно полезны для сравнения распределений между несколькими группами или наборами данных (см. Пример на рисунке 1). Выбор количества и ширины интервалов может сильно повлиять на внешний вид гистограммы, а выбор ширины полосы может сильно повлиять на внешний вид оценки плотности ядра.

Поскольку рассмотрение статистического распределения является более обычным явлением, чем рассмотрение прямоугольной диаграммы, сравнение прямоугольной диаграммы с функцией плотности вероятности (теоретическая гистограмма) для нормального распределения N (0, σ) может быть полезным инструментом. для понимания коробчатой диаграммы (рисунок 7).

Рисунок 8. Коробчатые диаграммы, отображающие перекос

См. Также

Ссылки

Дополнительная литература

Джон У. Тьюки (1977). Исследовательский анализ данных. Эддисон-Уэсли.
Бенджамини Ю. (1988). «Открытие коробки коробчатого сюжета». Американский статистик. 42 (4): 257–262. DOI : 10.2307 / 2685133. JSTOR 2685133.
Руссеу, П. Дж. ; Ruts, I.; Тьюки, Дж. У. (1999). "Багажник: двумерный коробчатый сюжет". Американский статистик. 53 (4): 382–387. DOI : 10.2307 / 2686061. JSTOR 2686061.

Внешние ссылки

На Wikimedia Commons есть материалы, связанные с Коробчатые диаграммы.

Онлайн-калькулятор коробчатых графиков с пояснениями и примерами ( Имеет пример beeswarm)
Beeswarm Boxplot - наложение полосовой диаграммы с колебаниями частоты поверх прямоугольной диаграммы
Создатель сложного онлайн-блочного графика с данными примера - см. Также BoxPlotR: веб-инструмент для создания коробчатые диаграммы Spitzer et al. Nature Methods 11, 121–122 (2014)