Расслабленное пересечение

редактировать

Расслабленное пересечение m множеств соответствует классическому пересечению между множествами, за исключением того, что разрешено ослабить несколько множеств, чтобы избежать пустой перекресток. Это понятие можно использовать для решения проблем удовлетворения ограничений, которые являются несовместимыми, путем ослабления небольшого количества ограничений. Когда метод ограниченной ошибки рассматривается для оценки параметров, ослабленное пересечение делает возможным быть устойчивым по отношению к некоторым выбросам.

Содержание

1 Определение
2 Пример
3 Расслабленное пересечение интервалов
4 Расслабленное пересечение прямоугольников
5 Расслабленное объединение
6 Закон Де Моргана
7 Ослабление контрагентов
8 Применение к ограниченной ошибке оценка
9 Ссылки

Определение

q-расслабленное пересечение m подмножеств $X 1,…, X m {\ displaystyle X_ {1}, \ dots, X_ {m} }$ ${\ displaystyle X_ {1}, \ dots, X_ {m}}$ из $R n {\ displaystyle R ^ {n}}$ ${\ displaystyle R ^ {n}}$ , обозначается $X {q} = ⋂ {q} X i {\ displaystyle X ^ {\ {q \}} = \ bigcap ^ {\ {q \}} X_ {i}}$ ${ \ Displaystyle X ^ {\ {q \}} = \ bigcap ^ {\ {q \}} X_ {i}}$ - это набор всех $x ∈ R n {\ displaystyle x \ in R ^ { n}}$ ${\ displaystyle x \ in R ^ {n}}$ , которые принадлежат всем $X i {\ displaystyle X_ {i}}$ ${\ displaystyle X_ {i}}$ , кроме $q {\ displaystyle q}$ $q$ максимум. Это определение проиллюстрировано на рисунке 1.

Рисунок 1. q-пересечение 6 множеств для q = 2 (красный), q = 3 (зеленый), q = 4 (синий), q = 5 (желтый).

Определите $λ (x) = card {i | x ∈ X i}. {\ displaystyle \ lambda (x) = {\ text {card}} \ left \ {i \ | \ x \ in X_ {i} \ right \}.}$ ${\ displaystyle \ lambda (x) = {\ text {card}} \ left \ {i \ | \ x \ in X_ {i} \ right \}.}$

У нас есть $X {q} = λ - 1 ([m - q, m]). {\ displaystyle X ^ {\ {q \}} = \ lambda ^ {- 1} ([mq, m]).}$ ${\ displaystyle X ^ {\ {q \}} = \ lambda ^ {- 1} ([mq, m]).}$

Характеристика q-релаксированного пересечения - это инверсия множества проблема.

Пример

Рассмотрим 8 интервалов: $X 1 = [1, 4], {\ displaystyle X_ {1} = [1,4],}$ ${\ displaystyle X_ {1} = [1,4],}$ $X 2 = [2, 4], {\ displaystyle X_ {2} = \ [2,4],}$ ${\ displaystyle X_ {2} = \ [2,4],}$ $X 3 = [2, 7], {\ displaystyle X_ {3} = [2,7],}$ ${\ displaystyle X_ { 3} = [2,7],}$ $Икс 4 = [6, 9], {\ displaystyle X_ {4} = [6,9],}$ ${\ displaystyle X_ {4} = [6,9],}$ $X 5 = [3, 4], {\ displaystyle X_ {5} = [3,4 ],}$ ${\ displaystyle X_ {5} = [3,4],}$ $X 6 = [3, 7]. {\ displaystyle X_ {6} = [3,7].}$ ${\ displaystyle X_ {6} = [3,7].}$

У нас есть

$X {0} = ∅, {\ displaystyle X ^ {\ {0 \}} = \ emptyset,}$ ${\ displaystyle X ^ {\ {0 \}} = \ emptyset,}$ $Икс {1} = [3, 4], {\ displaystyle X ^ {\ {1 \}} = [3,4],}$ ${\ displaystyle X ^ {\ {1 \}} = [3,4],}$ $X {2} = [3, 4], {\ displaystyle X ^ {\ {2 \}} = [3,4],}$ ${\ displaystyle X ^ {\ { 2 \}} = [3,4],}$ $X {3} = [2, 4] ∪ [6, 7], {\ displaystyle X ^ {\ {3 \}} = [2, 4] \ чашка [6,7],}$ ${ \ Displaystyle X ^ {\ {3 \}} = [2,4] \ чашка [6,7],}$ $X {4} = [2, 7], {\ displaystyle X ^ {\ {4 \}} = [2,7],}$ ${\ displaystyle X ^ {\ {4 \}} = [2,7],}$ $X {5} = [1, 9], {\ displaystyle X ^ {\ {5 \}} = [1,9],}$ ${\ displaystyle X ^ {\ {5 \}} = [1,9],}$ $X {6} =] - ∞, ∞ [. {\ displaystyle X ^ {\ {6 \}} =] - \ infty, \ infty [.}$ ${\ displaystyle X ^ {\ {6 \}} =] - \ infty, \ infty [.}$

Расслабленное пересечение интервалов

Расслабленное пересечение интервалов не обязательно является интервалом. Таким образом, мы берем интервальную оболочку результата. Если $X i {\ displaystyle X_ {i}}$ $X_ {i}$ представляют собой интервалы, ослабленное пересечение может быть вычислено со сложностью m.log (m) с использованием алгоритма Марзулло. Достаточно отсортировать все нижние и верхние границы m интервалов, чтобы представить функцию $λ {\ displaystyle \ lambda}$ $\ lambda$ . Тогда мы легко получаем набор

$X {q} = λ - 1 ([m - q, m]) {\ displaystyle X ^ {\ {q \}} = \ lambda ^ {- 1} ([mq, m])}$ ${\ displaystyle X ^ {\ {q \}} = \ lambda ^ {- 1} ([mq, m])}$

что соответствует объединению интервалов. Затем мы возвращаем наименьший интервал, содержащий это объединение.

На рисунке 2 показана функция $λ (x) {\ displaystyle \ lambda (x)}$ $\ lambda (x)$ , связанная с предыдущим примером.

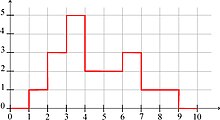
Рисунок 2. Функция принадлежности множеству, связанная с 6 интервалами.

Расслабленное пересечение прямоугольников

Для вычисления q-расслабленного пересечения m прямоугольников $R n {\ displaystyle R ^ {n}}$ ${\ displaystyle R ^ {n}}$ , мы проецируем все m прямоугольников относительно n осей. Для каждой из n групп по m интервалов вычисляем q-релаксированное пересечение. Мы возвращаем декартово произведение n результирующих интервалов. На рис. 3 показано 4-ослабленное пересечение 6 прямоугольников. Каждая точка красного квадрата принадлежит 4 из 6 квадратов.

Рис. 3. Красный прямоугольник соответствует 4-расслабленному пересечению 6 прямоугольников

Расслабленное объединение

q-расслабленное объединение $X 1,…, X m {\ displaystyle X_ {1}, \ dots, X_ {m}}$ ${\ displaystyle X_ {1}, \ dots, X_ {m}}$ определяется как

$⋃ {q} X i = ⋂ {m - 1 - q} X i {\ displaystyle {\ overset {\ {q \}} {\ bigcup}} X_ {i} = \ bigcap ^ {\ {m-1-q \}} X_ {i}}$ ${\ displaystyle {\ overset {\ {q \}} {\ bigcup}} X_ {i} = \ bigcap ^ {\ {m-1-q \}} X_ {i}}$

Обратите внимание, что когда q = 0, расслабленное объединение / пересечение соответствует к классическому объединению / пересечению. Точнее, у нас есть

$⋂ {0} X i = ⋂ X i {\ displaystyle \ bigcap ^ {\ {0 \}} X_ {i} = \ bigcap X_ {i}}$ ${\ displaystyle \ bigcap ^ {\ {0 \}} X_ {i} = \ bigcap X_ {i}}$

$⋃ {0} Икс я = ⋃ Икс я {\ displaystyle {\ overset {\ {0 \}} {\ bigcup}} X_ {i} = \ bigcup X_ {i}}$ ${\ displaystyle {\ overset {\ {0 \}} {\ bigcup }} X_ {i} = \ bigcup X_ {i}}$

Закон Де Моргана

Если $X ¯ {\ displaystyle {\ overline {X}}}$ ${\ overline {X}}$ обозначает дополнительный набор $X i {\ displaystyle X_ {i}}$ $X_ {i}$ , у нас есть

$⋂ {q} Икс я ¯ = ⋃ {q} Икс я ¯ {\ displaystyle {\ overline {\ bigcap ^ {\ {q \}} X_ {i}}} = {\ overset {\ { q \}} {\ bigcup}} {\ overline {X_ {i}}}}$ ${\ displaystyle {\ overline {\ bigcap ^ {\ {q \}} X_ {i}}} = {\ overset {\ {q \}} {\ bigcup}} {\ overline {X_ {i}}}}$

$⋃ {q} X i ¯ = ⋂ {q} X i ¯. {\ displaystyle {\ overline {{\ overset {\ {q \}} {\ bigcup}} X_ {i}}} = \ bigcap ^ {\ {q \}} {\ overline {X_ {i}}}. }$ ${\ displaystyle {\ overline {{\ overset {\ {q \}} {\ bigcup}} X_ {i}}} = \ bigcap ^ {\ {q \}} {\ overline {X_ {i}}}.}$

Как следствие

$⋂ {q} X i ¯ = ⋃ {m - q - 1} X i ¯ = ⋂ {m - q - 1} X i ¯ {\ displaystyle {\ overline {\ bigcap \ limits ^ {\ {q \}} X_ {i}}} = {\ overline {{\ overset {\ {mq-1 \}} {\ bigcup}} X_ {i}}} = \ bigcap ^ {\ {mq-1 \}} {\ overline {X_ {i}}}}$ ${\ displaystyle {\ overline {\ bigcap \ limits ^ {\ {q \}} X_ {i}}} = {\ overline {{\ overset {\ {mq-1 \}} {\ bigcup}} X _ {я}}} = \ bigcap ^ {\ {mq-1 \}} {\ overline {X_ {i}}}}$

Ослабление контрагентов

Пусть $C 1,…, C m {\ displaystyle C_ {1}, \ точек, C_ {m}}$ ${\ displaystyle C_ {1}, \ dots, C_ {m}}$ быть m подрядчиками для наборов $X 1,…, X m {\ displaystyle X_ {1}, \ dots, X_ {m} }$ ${\ displaystyle X_ {1}, \ dots, X_ {m}}$ , тогда

$C ([x]) = ⋂ {q} C i ([x]). {\ displaystyle C ([x]) = \ bigcap ^ {\ {q \}} C_ {i} ([x]).}$ ${\ displaystyle C ([x]) = \ bigcap ^ {\ {q \}} C_ {i} ([x]).}$

является подрядчиком для $X {q} {\ displaystyle X ^ {\ {q \}}}$ ${\ displaystyle X ^ {\ {q \}}}$ и

$C ¯ ([x]) = ⋂ {m - q - 1} C ¯ i ([x]) {\ displaystyle {\ overline {C }} ([x]) = \ bigcap ^ {\ {mq-1 \}} {\ overline {C}} _ {i} ([x])}$ ${\ displaystyle {\ overline {C}} ([x]) = \ bigcap ^ {\ {mq-1 \}} {\ overline {C}} _ {i} ([x])}$

является подрядчиком для $X ¯ { q} {\ displaystyle {\ overline {X}} ^ {\ {q \}}}$ ${\ displaystyle {\ overline {X}} ^ {\ {q \} }}$ , где

$C ¯ 1,…, C ¯ m {\ displaystyle {\ overline {C} } _ {1}, \ dots, {\ overline {C}} _ {m}}$ ${\ displaystyle { \ overline {C}} _ {1}, \ dots, {\ overline {C}} _ {m}}$

- подрядчики для

$X ¯ 1,…, X ¯ m. {\ displaystyle {\ overline {X}} _ {1}, \ dots, {\ overline {X}} _ {m}.}$ ${\ displaystyle {\ overline {X}} _ {1}, \ dots, {\ overline {X}} _ {m}.}$

В сочетании с алгоритмом ветвей и границ, например как SIVIA (Установить инверсию с помощью интервального анализа), можно вычислить q-расслабленное пересечение m подмножеств $R n {\ displaystyle R ^ {n}}$ ${\ displaystyle R ^ {n}}$ .

Применение для оценки ограниченной ошибки

Q-релаксирующее пересечение может использоваться для надежной локализации или для отслеживания.

Надежные наблюдатели также могут быть реализованы с использованием ослабленных пересечений, чтобы быть устойчивыми по отношению к выбросам.

Мы предлагаем здесь простой пример для иллюстрации метода. Рассмотрим модель, выход i-й модели которой задается как

$fi (p) = 1 2 π p 2 exp ⁡ (- (ti - p 1) 2 2 p 2) {\ displaystyle f_ {i} (p) = {\ frac {1} {\ sqrt {2 \ pi p_ {2}}}} \ exp (- {\ frac {(t_ {i} -p_ {1}) ^ {2}} {2p_ {2}) }})}$ ${\ displaystyle f_ {i} (p) = {\ frac {1} {\ sqrt {2 \ pi p_ {2}}}} \ exp (- {\ frac {(t_ {i} -p_ {1}) ^ {2}} {2p_ {2}}})}$

где $p ∈ R 2 {\ displaystyle p \ in R ^ {2}}$ ${\ displaystyle p \ in R ^ {2}}$ . Предположим, что у нас есть

$fi (p) ∈ [yi] {\ displaystyle f_ {i} (p) \ in [y_ {i}]}$ ${\ displaystyle f_ {i} (p) \ in [y_ {i}]}$

где $ti {\ displaystyle t_ {i}}$ $t_ {i}$ и $[yi] {\ displaystyle [y_ {i}]}$ ${\ displaystyle [y_ {i}]}$ задаются следующим списком

${(1, [0; 0.2]), ( 2, [0,3; 2]), (3, [0,3; 2]), (4, [0,1; 0,2]), (5, [0,4; 2]), (6, [- 1; 0,1])} {\ displaystyle \ {(1, [0; 0,2]), (2, [0,3; 2]), (3, [0,3; 2]), (4, [0,1; 0,2]), (5, [0,4 ; 2]), (6, [- 1; 0,1]) \}}$ ${\ displaystyle \ {(1, [0; 0,2]), (2, [0,3; 2]), (3, [0,3; 2]), (4, [0,1; 0,2] ]), (5, [0,4; 2]), (6, [- 1; 0,1]) \}}$

Множества $λ - 1 (q) {\ displaystyle \ lambda ^ {- 1} (q)}$ ${\ displaystyle \ lambda ^ {- 1} (q)}$ для различных $q {\ displaystyle q}$ $q$ изображены на рисунке 4.

Рисунок 4. Набор всех векторов параметров, согласующихся ровно с 6-q столбцами данных (окрашенными красным), для q = 1,2,3,4,5.

Ссылки