Параболоидальные координаты

Параболоидальные координаты - это трехмерные ортогональные координаты, которые обобщают двумерные параболические координаты. Они обладают эллиптическими параболоидами как однокоординатными поверхностями. По существу, их следует отличать от параболических цилиндрических координат и параболических координат вращения, которые также являются обобщениями двумерных параболических координат. Координатные поверхности первых представляют собой параболические цилиндры, а координатные поверхности вторых - круговые параболоиды. ${\ Displaystyle (\ му, \ ню, \ лямбда)}$

В отличие от цилиндрических и вращательных параболических координат, но аналогично соответствующим эллипсоидальным координатам, координатные поверхности параболоидальной системы координат не создаются путем вращения или проецирования какой-либо двумерной ортогональной системы координат.

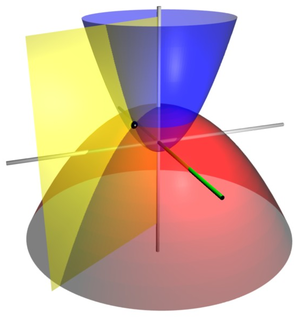Координатные поверхности трехмерных параболоидальных координат.

• 1 Основные формулы
• 2 Масштабные коэффициенты
• 3 Дифференциальные операторы
• 4 Приложения
• 5 ссылки
• 6 Библиография
• 7 Внешние ссылки

Декартовы координаты могут быть получены из эллипсоидальных координат с помощью уравнений ${\ Displaystyle (х, у, г)}$${\ Displaystyle (\ му, \ ню, \ лямбда)}$

${\ Displaystyle х ^ {2} = {\ гидроразрыва {4} {bc}} (\ mu -b) (b- \ nu) (b- \ lambda)}$

${\ Displaystyle у ^ {2} = {\ гидроразрыва {4} {bc}} (\ mu -c) (c- \ nu) (\ lambda -c)}$

${\ displaystyle z = \ mu + \ nu + \ lambda -bc}$

с

${\ displaystyle \ mugt; bgt; \ lambdagt; cgt; \ nugt; 0}$

Следовательно, поверхности постоянных являются открывающимися вниз эллиптическими параболоидами: ${\ displaystyle \ mu}$

${\ displaystyle {\ frac {x ^ {2}} {\ mu -b}} + {\ frac {y ^ {2}} {\ mu -c}} = - 4 (z- \ mu)}$

Точно так же поверхности постоянных являются открывающимися вверх эллиптическими параболоидами, ${\ displaystyle \ nu}$

${\ displaystyle {\ frac {x ^ {2}} {b- \ nu}} + {\ frac {y ^ {2}} {c- \ nu}} = 4 (z- \ nu)}$

тогда как поверхности константы являются гиперболическими параболоидами: ${\ displaystyle \ lambda}$

${\ displaystyle {\ frac {x ^ {2}} {b- \ lambda}} - {\ frac {y ^ {2}} {\ lambda -c}} = 4 (z- \ lambda)}$

Масштабные коэффициенты для параболоидальных координат равны ${\ Displaystyle (\ му, \ ню, \ лямбда)}$

${\ Displaystyle ч _ {\ му} = \ влево [{\ гидроразрыва {\ влево (\ му - \ ню \ вправо) \ влево (\ му - \ лямбда \ вправо)} {\ влево (\ му -b \ вправо) \ left (\ mu -c \ right)}} \ right] ^ {1/2}}$

${\ Displaystyle час _ {\ ню} = \ влево [{\ гидроразрыва {\ влево (\ му - \ ню \ право) \ влево (\ лямбда - \ ню \ вправо)} {\ влево (б- \ ню \ вправо) \ left (c- \ nu \ right)}} \ right] ^ {1/2}}$

${\ Displaystyle час _ {\ лямбда} = \ влево [{\ гидроразрыва {\ влево (\ лямбда - \ ню \ вправо) \ влево (\ му - \ лямбда \ вправо)} {\ влево (б- \ лямбда \ вправо) \ left (\ lambda -c \ right)}} \ right] ^ {1/2}}$

Следовательно, бесконечно малый элемент объема равен

${\ Displaystyle dV = {\ гидроразрыва {(\ му - \ ню) (\ му - \ лямбда) (\ лямбда - \ ню)} {\ влево [(\ му -b) (\ му -c) (b- \ nu) (c- \ nu) (b- \ lambda) (\ lambda -c) \ right] ^ {1/2}}} \ d \ lambda d \ mu d \ nu}$

Общие дифференциальные операторы могут быть выражены в координатах путем подстановки масштабных множителей в общие формулы для этих операторов, которые применимы к любым трехмерным ортогональным координатам. Например, оператор градиента представляет ${\ Displaystyle (\ му, \ ню, \ лямбда)}$

${\ displaystyle \ nabla = \ left [{\ frac {\ left (\ mu -b \ right) \ left (\ mu -c \ right)} {\ left (\ mu - \ nu \ right) \ left (\ mu - \ lambda \ right)}} \ right] ^ {1/2} \ mathbf {e} _ {\ mu} {\ frac {\ partial} {\ partial \ mu}} + \ left [{\ frac { \ left (b- \ nu \ right) \ left (c- \ nu \ right)} {\ left (\ mu - \ nu \ right) \ left (\ lambda - \ nu \ right)}} \ right] ^ {1/2} \ mathbf {e} _ {\ nu} {\ frac {\ partial} {\ partial \ nu}} + \ left [{\ frac {\ left (b- \ lambda \ right) \ left ( \ lambda -c \ right)} {\ left (\ lambda - \ nu \ right) \ left (\ mu - \ lambda \ right)}} \ right] ^ {1/2} \ mathbf {e} _ {\ лямбда} {\ frac {\ partial} {\ partial \ lambda}}}$

а лапласиан равен

${\ displaystyle {\ begin {align} \ nabla ^ {2} = amp; \ left [{\ frac {\ left (\ mu -b \ right) \ left (\ mu -c \ right)} {\ left (\ mu - \ nu \ right) \ left (\ mu - \ lambda \ right)}} \ right] ^ {1/2} {\ frac {\ partial} {\ partial \ mu}} \ left [(\ mu - б) ^ {1/2} (\ mu -c) ^ {1/2} {\ frac {\ partial} {\ partial \ mu}} \ right] \\ amp; + \ left [{\ frac {\ left (b- \ nu \ right) \ left (c- \ nu \ right)} {\ left (\ mu - \ nu \ right) \ left (\ lambda - \ nu \ right)}} \ right] ^ {1 / 2} {\ frac {\ partial} {\ partial \ nu}} \ left [(b- \ nu) ^ {1/2} (c- \ nu) ^ {1/2} {\ frac {\ partial } {\ partial \ nu}} \ right] \\ amp; + \ left [{\ frac {\ left (b- \ lambda \ right) \ left (\ lambda -c \ right)} {\ left (\ lambda - \ nu \ right) \ left (\ mu - \ lambda \ right)}} \ right] ^ {1/2} {\ frac {\ partial} {\ partial \ lambda}} \ left [(b- \ lambda) ^ {1/2} (\ lambda -c) ^ {1/2} {\ frac {\ partial} {\ partial \ lambda}} \ right] \ end {выровнено}}}$

Параболоидальные координаты могут быть полезны для решения некоторых дифференциальных уравнений в частных производных. Например, уравнение Лапласа и уравнение Гельмгольца оба разъемные в параболоидальных координатах. Следовательно, координаты могут использоваться для решения этих уравнений в геометриях с параболоидальной симметрией, то есть с граничными условиями, заданными на сечениях параболоидов.

Уравнение Гельмгольца есть. Принимая, разделенные уравнения имеют вид ${\ displaystyle (\ nabla ^ {2} + k ^ {2}) \ psi = 0}$${\ Displaystyle \ пси = М (\ му) N (\ ню) \ лямбда (\ лямбда)}$

${\ displaystyle {\ begin {align} amp; (\ mu -b) (\ mu -c) {\ frac {d ^ {2} M} {d \ mu ^ {2}}} + {\ frac {1} {2}} \ left [2 \ mu - (b + c) \ right] {\ frac {dM} {d \ mu}} + \ left [k ^ {2} \ mu ^ {2} + \ alpha _ {3} \ mu - \ alpha _ {2} \ right] M = 0 \\ amp; (b- \ nu) (c- \ nu) {\ frac {d ^ {2} N} {d \ nu ^ { 2}}} + {\ frac {1} {2}} \ left [2 \ nu - (b + c) \ right] {\ frac {dN} {d \ nu}} + \ left [k ^ {2 } \ nu ^ {2} + \ alpha _ {3} \ nu - \ alpha _ {2} \ right] N = 0 \\ amp; (b- \ lambda) (\ lambda -c) {\ frac {d ^ {2} \ Lambda} {d \ lambda ^ {2}}} - {\ frac {1} {2}} \ left [2 \ lambda - (b + c) \ right] {\ frac {d \ Lambda} {d \ lambda}} - \ left [k ^ {2} \ lambda ^ {2} + \ alpha _ {3} \ lambda - \ alpha _ {2} \ right] \ Lambda = 0 \\\ end {выровнено }}}$

где и - две постоянные разделения. Точно так же разделенные уравнения для уравнения Лапласа могут быть получены путем установки в вышеупомянутом. ${\ displaystyle \ alpha _ {2}}$${\ displaystyle \ alpha _ {3}}$${\ displaystyle k = 0}$

Каждое из разделенных уравнений можно представить в виде уравнения Бэра. Однако прямое решение уравнений затруднено отчасти потому, что константы разделения и присутствуют одновременно во всех трех уравнениях. ${\ displaystyle \ alpha _ {2}}$${\ displaystyle \ alpha _ {3}}$

Следуя описанному выше подходу, параболоидальные координаты использовались для определения электрического поля, окружающего проводящий параболоид.

• Лью Ян Вун, LC, Willatzen M (2011). Разделимые краевые задачи в физике. Wiley-VCH. ISBN   978-3-527-41020-0.
• Морс PM, Фешбах H (1953). Методы теоретической физики, часть I. Нью-Йорк: Макгроу-Хилл. п. 664. ISBN   0-07-043316-X. LCCN   52011515.
• Маргенау Х., Мерфи GM (1956). Математика физики и химии. Нью-Йорк: Д. ван Ностранд. стр.  184 -185. LCCN   55010911.
• Корн Г.А., Корн Т.М. (1961). Математический справочник для ученых и инженеров. Нью-Йорк: Макгроу-Хилл. п.  180. LCCN   59014456. ASIN B0000CKZX7.
• Арфкен Г (1970). Математические методы для физиков (2-е изд.). Орландо, Флорида: Academic Press. С. 119–120.
• Зауэр Р., Сабо I (1967). Mathematische Hilfsmittel des Ingenieurs. Нью-Йорк: Springer Verlag. п. 98. LCCN   67025285.
• Цвиллинджер Д. (1992). Справочник по интеграции. Бостон, Массачусетс: Джонс и Бартлетт. п. 114. ISBN   0-86720-293-9. То же, что и Morse amp; Feshbach (1953), заменяя u k на ξ k.
• Мун П., Спенсер Д.Е. (1988). «Параболоидальные координаты (μ, ν, λ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд., 3-е изд.). Нью-Йорк: Springer-Verlag. С. 44–48 (Таблица 1.11). ISBN   978-0-387-18430-2.

• MathWorld описание конфокальных параболоидальных координат