Матроидный многогранник

В математике матроидный многогранник, также называемый базисным матроидным многогранником (или базисным матроидным многогранником ), чтобы отличать его от других многогранников, полученных из матроида, представляет собой многогранник, построенный с помощью баз матроида. Учитывая матроидом, матроид многогранник является выпуклой оболочкой из индикаторных векторов фундаментов. ${\ displaystyle M}$${\ displaystyle P_ {M}}$ ${\ displaystyle M}$

• 1 Определение
• 2 Примеры
• 3 свойства
• 4 Связанные многогранники
  • 4.1 Матроидный многогранник независимости
  • 4.2 Флаг матроидного многогранника
• 5 ссылки

Позвольте быть матроидом на элементах. Учитывая основу из, то индикатор вектор из IS ${\ displaystyle M}$ ${\ displaystyle n}$${\ Displaystyle B \ substeq \ {1, \ точки, п \}}$${\ displaystyle M}$${\ displaystyle B}$

${\ displaystyle \ mathbf {e} _ {B}: = \ sum _ {i \ in B} \ mathbf {e} _ {i},}$

где - стандартный й единичный вектор в. Матроидом многогранник является выпуклой оболочкой множества ${\ Displaystyle \ mathbf {е} _ {я}}$${\ displaystyle i}$${\ Displaystyle \ mathbb {R} ^ {п}}$ ${\ displaystyle P_ {M}}$

${\ displaystyle \ {\ mathbf {e} _ {B} \ mid B {\ text {является основой}} M \} \ substeq \ mathbb {R} ^ {n}.}$

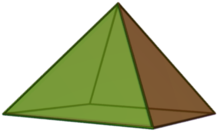
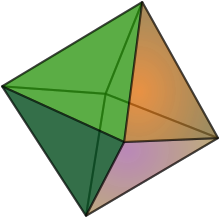
Квадратная пирамида Октаэдр

• Пусть - матроид ранга 2 на 4 элементах с базами ${\ displaystyle M}$

${\ Displaystyle {\ mathcal {B}} (М) = \ {\ {1,2 \}, \ {1,3 \}, \ {1,4 \}, \ {2,3 \}, \ { 2,4 \} \}.}$

То есть все двухэлементные подмножества за исключением. Соответствующие векторы индикатора являются ${\ displaystyle \ {1,2,3,4 \}}$${\ displaystyle \ {3,4 \}}$${\ Displaystyle {\ mathcal {B}} (М)}$

${\ Displaystyle \ {\ {1,1,0,0 \}, \ {1,0,1,0 \}, \ {1,0,0,1 \}, \ {0,1,1,0 \}, \ {0,1,0,1 \} \}.}$

Матроидом многогранник IS ${\ displaystyle M}$

${\ Displaystyle P_ {M} = {\ text {conv}} \ {\ {1,1,0,0 \}, \ {1,0,1,0 \}, \ {1,0,0,1 \}, \ {0,1,1,0 \}, \ {0,1,0,1 \} \}.}$

Эти точки образуют четыре равносторонних треугольника в точке, поэтому его выпуклая оболочка по определению является квадратной пирамидой. ${\ displaystyle \ {1,1,0,0 \}}$

• Позвольте быть матроидом ранга 2 на 4 элементах с базами, которые все 2-элементные подмножества. Соответствующий многогранник матроида - октаэдр. Обратите внимание, что многогранник из предыдущего примера содержится в. ${\ displaystyle N}$${\ displaystyle \ {1,2,3,4 \}}$${\ displaystyle P_ {N}}$ ${\ displaystyle P_ {M}}$${\ displaystyle P_ {N}}$
• Если - равномерный матроид ранга на элементах, то матроидный многогранник является гиперсимплексом. ${\ displaystyle M}$ ${\ displaystyle r}$${\ displaystyle n}$${\ displaystyle P_ {M}}$ ${\ displaystyle \ Delta _ {n} ^ {r}}$

• Многогранник матроидов содержится в гиперсимплексе, где - ранг связанного матроида, а - размер основного множества связанного матроида. Более того, вершины являются подмножеством вершин. ${\ displaystyle \ Delta _ {n} ^ {r}}$${\ displaystyle r}$${\ displaystyle n}$${\ displaystyle P_ {M}}$${\ displaystyle \ Delta _ {n} ^ {r}}$
• Каждое ребро матроидного многогранника является параллельным переносом для некоторого основного набора связанного матроида. Другими словами, ребра соответствуют в точности парам оснований, которые удовлетворяют свойству обмена базисом : для некоторых Из-за этого свойства каждая длина ребра является квадратным корнем из двух. В более общем смысле, семейства множеств, для которых выпуклая оболочка индикаторных векторов имеет длину ребер один или квадратный корень из двух, в точности являются дельта-матроидами. ${\ displaystyle P_ {M}}$${\ displaystyle e_ {i} -e_ {j}}$${\ displaystyle i, j \ in E}$${\ displaystyle P_ {M}}$${\ displaystyle B, B '}$ ${\ displaystyle B '= B \ setminus {я \ чашка j}}$${\ displaystyle i, j \ in E.}$
• Многогранники матроидов являются членами семейства обобщенных пермутоэдров.
• Позвольте быть функцией ранга матроида. Матроидом многогранник может быть однозначно записан в виде подписанной суммы Минковского из симплексов : ${\ displaystyle r: 2 ^ {E} \ rightarrow \ mathbb {Z}}$${\ displaystyle M}$${\ displaystyle P_ {M}}$

${\ Displaystyle P_ {M} = \ sum _ {A \ substeq E} {\ tilde {\ beta}} (M / A) \ Delta _ {EA}}$

где - базовый набор матроида, а - бета-инвариант со знаком: ${\ displaystyle E}$${\ displaystyle M}$${\ Displaystyle \ бета (М)}$${\ displaystyle M}$

${\ Displaystyle {\ тильда {\ бета}} (М) = (- 1) ^ {г (М) +1} \ бета (М),}$

${\ Displaystyle \ бета (M) = (- 1) ^ {r (M)} \ sum _ {X \ substeq E} (- 1) ^ {| X |} r (X).}$

${\ Displaystyle P_ {M}: = \ left \ {{\ textbf {x}} \ in \ mathbb {R} _ {+} ^ {E} ~ | ~ \ sum _ {e \ in U} {\ textbf {x}} (e) \ leq r (U), \ forall U \ substeq E \ right \}}$

Матроидный многогранник независимости

Матроид многогранник независимости или матроид независимости многогранник является выпуклой оболочкой множества

${\ displaystyle \ {\, \ mathbf {e} _ {I} \ mid I {\ text {является независимым набором}} M \, \} \ substeq \ mathbb {R} ^ {n}.}$

Матроидный (базисный) многогранник является гранью матроидного многогранника независимости. Учитывая ранг матроида, многогранник матроидов независимости равен полиматроиду, определяемому. ${\ displaystyle \ psi}$${\ displaystyle M}$ ${\ displaystyle \ psi}$

Пометить матроидный многогранник

Матроидный многогранник флагов - еще один многогранник, построенный из основ матроидов. Флаг является строго возрастающей последовательностью ${\ displaystyle {\ mathcal {F}}}$

${\ Displaystyle F ^ {1} \ подмножество F ^ {2} \ subset \ cdots \ subset F ^ {m} \,}$

конечных множеств. Позвольте быть мощность множества. Два матроида и называются согласованными, если их ранговые функции удовлетворяют ${\ displaystyle k_ {i}}$${\ displaystyle F_ {i}}$${\ displaystyle M}$${\ displaystyle N}$

${\ displaystyle r_ {M} (Y) -r_ {M} (X) \ leq r_ {N} (Y) -r_ {N} (X) {\ text {для всех}} X \ subset Y \ substeq E. \,}$

Даны попарно согласованные матроиды на основании, заданные рангами, рассмотрим набор флагов, где - основа матроида и. Такой набор флагов представляет собой матроид флагов. Матроиды называются составными частями. Для каждого флага в матроиде флагов, пусть будет сумма векторов индикаторов каждого базиса в ${\ displaystyle M_ {1}, \ dots, M_ {m}}$${\ displaystyle E}$${\ displaystyle r_ {1} lt;\ cdots lt;r_ {m}}$${\ displaystyle (B_ {1}, \ dots, B_ {m})}$${\ displaystyle B_ {i}}$${\ displaystyle M_ {i}}$${\ Displaystyle B_ {1} \ subset \ cdots \ subset B_ {m}}$ ${\ displaystyle {\ mathcal {F}}}$${\ displaystyle M_ {1}, \ dots, M_ {m}}$${\ displaystyle {\ mathcal {F}}}$${\ displaystyle B = (B_ {1}, \ dots, B_ {m})}$${\ displaystyle {\ mathcal {F}}}$${\ displaystyle v_ {B}}$${\ displaystyle B}$

${\ Displaystyle v_ {B} = v_ {B_ {1}} + \ cdots + v_ {B_ {m}}. \,}$

Учитывая флаг матроид, то флаг матроидом многогранник является выпуклой оболочкой множества ${\ displaystyle {\ mathcal {F}}}$ ${\ Displaystyle P _ {\ mathcal {F}}}$

${\ displaystyle \ {v_ {B} \ mid B {\ text {- это флаг в}} {\ mathcal {F}} \}.}$

Матроидный многогранник флага может быть записан как сумма Минковского (базисных) матроидных многогранников составляющих матроид:

${\ Displaystyle P _ {\ mathcal {F}} = P_ {M_ {1}} + \ cdots + P_ {M_ {k}}. \,}$

1. ^ Grötschel, Мартин (2004), "Системы множеств однородных множеств, циклы в матроидах и связанные многогранники", The Sharpest Cut: The Impact of Manfred Padberg и его работы, MPS / SIAM Ser. Optim., SIAM, Philadelphia, PA, стр. 99–120, MR   2077557 CS1 maint: обескураженный параметр ( ссылка ). См., В частности, примечания после предложения 8.20 на стр. 114.
2. ^ ^{а б} Гельфанд И.М.; Гореский, РМ; Макферсон, РД; Серганова, В.В. (1987). «Комбинаторные геометрии, выпуклые многогранники и клетки Шуберта». Успехи в математике. 63 (3): 301–316. DOI : 10.1016 / 0001-8708 (87) 90059-4.
3. ^ ^{a b} Ардила, Федерико; Бенедетти, Каролина; Докер, Джеффри (2010). «Матроидные многогранники и их объемы». Дискретная и вычислительная геометрия. 43 (4): 841–854. arXiv : 0810.3947. DOI : 10.1007 / s00454-009-9232-9.
4. ^ ^{a b} Боровик, Александр В.; Гельфанд И.М.; Белый, Нил (2013). "Матроиды Кокстера". Успехи в математике. 216. DOI : 10.1007 / 978-1-4612-2066-4.