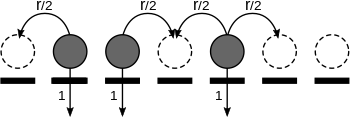
Процесс контакта (математика)

Процесс контакта (на 1-D решетке): Активен сайты обозначены серыми кружками, а неактивные - пунктирными кружками. Активные сайты могут активировать неактивные сайты по обе стороны от них со скоростью r / 2 или становиться неактивными со скоростью 1.

контактный процесс - это стохастический процесс, используемый для моделирования населения рост на множестве сайтов $S\; \{\backslash \; displaystyle\; S\}$на графике, в котором занятые сайты становятся вакантными с постоянной скоростью, а свободные сайты становятся занятыми со скоростью, пропорциональной к количеству занятых соседних участков. Следовательно, если мы обозначим через $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$константу пропорциональности, каждый сайт останется занятым в течение случайного периода времени, который равен экспоненциально распределенному параметру 1 и помещает потомков на каждом вакантном соседнем сайте во время событий пуассоновского процесса параметра $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$в течение этого периода. Все процессы независимы друг от друга и от случайного периода времени, когда узлы остаются занятыми. Процесс контакта также можно интерпретировать как модель распространения инфекции, рассматривая частицы как бактерию, распространяющуюся на людей, находящихся в местах $S\; \{\backslash \; displaystyle\; S\}$, занятых сайты соответствуют инфицированным, а свободные - здоровым.

Основное значение, представляющее интерес, - это количество частиц в процессе, скажем $N\; t\; \{\backslash \; displaystyle\; N\_\; \{t\}\}$в первой интерпретации, что соответствует количество зараженных сайтов во втором. Следовательно, этот процесс продолжается, когда число частиц всегда положительно, что соответствует случаю, когда во втором случае всегда есть инфицированные особи. Для любого бесконечного графа $S\; \{\backslash \; displaystyle\; S\}$существует положительное и конечное критическое значение $\lambda \; c\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{c\}\}$, так что если $\lambda >\lambda \; c\; \{\backslash \; displaystyle\; \backslash \; lambda>\backslash \; lambda\; \_\; \{c\}\}$тогда выживание процесса, начиная с конечного числа частиц, происходит с положительной вероятностью, а если , то их исчезновение почти наверняка. с помощью reductio ad absurdum и теоремы о бесконечной обезьяне выживание процесса эквивалентно $N\; t\; \to \; \infty \; \{\backslash \; displaystyle\; N\_\; \{t\}\; \backslash \; to\; \backslash \; infty\}$, как $t\; \to \; \infty \; \{\backslash \; displaystyle\; t\; \backslash \; to\; \backslash \; infty\}$, тогда как вымирание эквивалентно $N\; t\; \to \; 0\; \{\backslash \; displaystyle\; N\_\; \{t\}\; \backslash \; to\; 0\}$, поскольку $t\; \to \; \infty \; \{\backslash \; displaystyle\; t\; \backslash \; to\; \backslash \; infty\}$, и поэтому естественно спросить, с какой скоростью $N\; t\; \to \; \infty \; \{\backslash \; displaystyle\; N\_\; \{\; t\}\; \backslash \; to\; \backslash \; infty\}$когда процесс выживает.

.

• 1 Математическое определение
• 2 Связь с просачиванием
• 3 Закон больших чисел для целых
• 4 Отмирание при критичности
• 5 Гипотеза Дарретта и центральная предельная теорема
• 6 источников

Если состояние процесса во время $t\; \{\backslash \; displaystyle\; t\}$равно $\xi \; t\; \{\backslash \; displaystyle\; \backslash \; xi\; \_\; \{\; t\}\}$, тогда сайт $x\; \{\backslash \; displaystyle\; x\}$в $S\; \{\backslash \; displaystyle\; S\}$занят, скажем, частица, если $\xi \; t\; (x)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; xi\; \_\; \{t\}\; (x)\; =\; 1\}$, и пустая, если $\xi \; t\; (x)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; xi\; \_\; \{t\}\; (x)\; =\; 0\}$. Процесс связи - это непрерывный марковский процесс с пространством состояний $\{0,\; 1\}\; S\; \{\backslash \; displaystyle\; \backslash \; \{0,1\; \backslash \}\; ^\; \{S\}\}$, где $S\; \{\backslash \; displaystyle\; S\}$- конечный или счетный граф, обычно $Z\; d\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{Z\}\; ^\; \{d\}\}$и частный случай системы взаимодействующих частиц. В частности, динамика основного процесса контакта определяется следующими скоростями перехода: на сайте $x\; \{\backslash \; displaystyle\; x\}$,

$1\; \to \; 0\; со\; скоростью\; 1,\; \{\backslash \; displaystyle\; 1\; \backslash \; rightarrow\; 0\; \backslash \; quad\; \{\backslash \; текст\; \{со\; скоростью\}\}\; 1,\}$

$0\; \to \; 1\; со\; скоростью\; \lambda \; \sum \; y:\; y\; \sim \; x\; \xi \; t\; (y),\; \{\backslash \; displaystyle\; 0\; \backslash \; rightarrow\; 1\; \backslash \; quad\; \{\backslash \; text\; \{at\; rate\}\}\; \backslash \; lambda\; \backslash \; sum\; \_\; \{y\; \backslash ,:\; \backslash ,\; y\; \backslash ,\; \backslash \; sim\; \backslash ,\; x\}\; \backslash \; xi\; \_\; \{t\}\; (y),\}$

, где сумма берется по всем соседям $y\; \{\backslash \; displaystyle\; y\}$из $x\; \{\backslash \; displaystyle\; x\}$в $S\; \{\backslash \; displaystyle\; S\}$. Это означает, что каждый сайт ждет экспоненциальное время с соответствующей скоростью, а затем переворачивается (так что 0 становится 1 и наоборот).

.