Круговой график

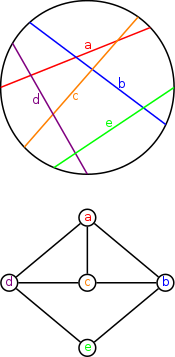
Круг с пятью хордами и соответствующий круговой график.

В теории графов круговой граф - это граф пересечений набора аккордов круга круга. То есть это неориентированный граф, вершины которого могут быть связаны с хордами окружности, так что две вершины смежны тогда и только тогда, когда соответствующие хорды пересекают друг друга.

• 1 Алгоритмическая сложность
• 2 Хроматическое число
• 3 Приложения
• 4 Связанные классы графов
• 5 Примечания
• 6 Ссылки
• 7 Внешние ссылки

Spinrad (1994) дает алгоритм времени O (n), который проверяет, является ли данный неориентированный граф с n вершинами круговым графом, и, если это так, строит набор хорд, которые его представляют.

Ряд других задач, которые NP-полны на общих графах, имеют алгоритмы с полиномиальным временем, когда они ограничены круговыми графами. Например, Kloks (1996) показал, что древовидная ширина кругового графа может быть определена и построено оптимальное разложение дерева за время O (n). Кроме того, минимальное заполнение (то есть хордовый граф с как можно меньшим количеством ребер, которое содержит данный круговой граф в качестве подграфа) может быть найдено за время O (n). Tiskin (2010) показал, что максимальная клика кругового графа может быть найдена за время O (n log n), а Nash Gregg (2010) показали, что максимальный независимый набор невзвешенного кругового графа может быть найден за время O (n min {d, α}), где d - параметр графа, известный как его плотность, а α - число независимости кругового графа.

Однако есть также проблемы, которые остаются NP-полными при ограничении круговыми графами. К ним относятся: минимальный доминирующий набор, минимальный связанный доминирующий набор и задачи минимального общего доминирующего набора.

Хорды, образующие 220-вершинный 5-хроматический круг без треугольников график Агеева (1996), нарисованный как расположение линий в гиперболической плоскости.

хроматическое число кругового графика - это минимальное количество цветов, которые можно использовать для раскраски хорд, чтобы никакие две пересекающиеся хорды не имели одинаковый цвет. Поскольку можно формировать круговые графы, в которых произвольно большие наборы хорд пересекают друг друга, хроматическое число кругового графа может быть сколь угодно большим, и определение хроматического числа кругового графа является NP-полным. Остается NP-полным, чтобы проверить, можно ли раскрасить круговой граф в четыре цвета. Унгер (1992) утверждал, что нахождение раскраски в три цвета может быть выполнено за полиномиальное время, но его описание этого результата опускает многие детали.

Несколько авторов исследовали проблемы раскраски ограниченных подклассов круговых графов в несколько цветов. В частности, для круговых графов, в которых никакие наборы из k или более хорд не пересекаются друг с другом, можно раскрасить граф всего с помощью $21\; \cdot \; 2\; k\; -\; 24\; k\; -\; 24\; \{\backslash \; displaystyle\; 21\; \backslash \; cdot\; 2\; ^\; \{k\}\; -24k-24\}$цветов. Один из способов заявить об этом состоит в том, что круговые графики являются $\chi \; \{\backslash \; displaystyle\; \backslash \; chi\}$-ограниченными. В частном случае, когда k = 3 (то есть для круговых графов без треугольников ), хроматическое число не превышает пяти, и это жестко: все круговые графы без треугольников могут быть окрашены в пять цветов., и существуют круговые графы без треугольников, требующие пяти цветов. Если круговой граф имеет обхват не менее пяти (т. Е. Он не содержит треугольников и четырехвершинных циклов), его можно раскрасить не более чем в три цвета. Проблема раскраски квадратов без треугольников эквивалентна задаче представления квадратных графов как изометрических подграфов декартовых произведений деревьев ; в этом соответствии количество цветов в раскраске соответствует количеству деревьев в представлении продукта.

Круговые графы возникают в VLSI физических дизайн как абстрактное представление для особого случая для прокладки проводов, известного как «двухконтактный». В данном случае это прямоугольник, все цепи двухполюсные, а выводы расположены по периметру прямоугольника. Легко видеть, что граф пересечений этих сетей - круговой граф. Одной из целей этапа прокладки проводов является обеспечение того, чтобы различные цепи оставались электрически отключенными, а их потенциальные пересекающиеся части должны быть разложены в разных проводящих слоях. Поэтому круговые диаграммы отражают различные аспекты этой проблемы маршрутизации.

Раскраски круговых графов также можно использовать для поиска книжных вложений произвольных графов: если вершины данного графа G расположены на окружности, а края графа G образуют хорды круг, то граф пересечений этих хорд является круговым графом, и раскраски этого кругового графа эквивалентны вложениям книг, которые соответствуют данной круговой компоновке. В этом эквиваленте количество цветов в раскраске соответствует количеству страниц во вложении книги.

Граф является круговым графом тогда и только тогда, когда он набора интервалов на линии. Это граф, в котором вершины соответствуют интервалам, а две вершины соединены ребром, если два интервала перекрываются, и ни одна из них не содержит другого.

граф пересечений набора интервалов на линии называется графом интервалов.

строковыми диаграммами, диаграммами пересечений кривые на плоскости, включая круговые графики как частный случай.

Every является круговым графом, как и каждый граф перестановок и каждый граф безразличия. Каждый внешнепланарный граф также является круговым графом.

• Агеев, А.А. (1996), «Круговой граф без треугольников с хроматическим числом 5 ", Дискретная математика, 152 (1–3): 295–298, doi : 10.1016 / 0012-365X (95) 00349-2.
• Агеев, А.А. (1999), «Каждый круговой график с обхватом не менее 5 может быть раскрашен в три цвета», Дискретная математика, 195 (1–3): 229–233, doi : 10.1016 / S0012-365X (98) 00192-7.
• Bandelt, H.-J.; Чепой, В.; Эппштейн, Д. (2010), «Комбинаторика и геометрия конечных и бесконечных квадратных графов», Журнал SIAM по дискретной математике, 24(4): 1399–1440, arXiv : 0905.4537, doi : 10.1137 / 090760301.
• Черны, Якуб (2007), «Раскрашивание круговых графиков», Электронные заметки по дискретной математике, 29 : 357–361, doi : 10.1016 / j.endm.2007.07.072.
• Гарей, MR ; Джонсон, Д.С. ; Миллер, Г. Л. ; Пападимитриу, К. (1980), «Сложность раскраски дуг окружности и хорд», Журнал SIAM по алгебраическим и дискретным методам, 1 (2): 216–227, doi : 10.1137 / 0601025.
• Гьярфас, А. (1985), «О хроматическом числе графов с несколькими интервалами и графов с перекрытием», Дискретная математика, 55(2): 161–166, doi : 10.1016 / 0012-365X (85) 90044-5. Цитируется по Агеев (1996).
• Гьярфас, А. ; Лехел, Дж. (1985), «Проблемы покрытия и раскраски для родственников интервалов», Дискретная математика, 55(2): 167–180, doi : 10.1016 / 0012- 365X (85) 90045-7. Цит. По Агеев (1996).
• Карапетян А. (1984), О графах пересечений совершенных дуг и хорд, канд. диссертация, Ин-т. математики, Новосибирск. Цитируется по Агеев (1996).
• Кейл, Дж. Марк (1993), «Сложность проблем доминирования в круговых графах», Дискретная прикладная математика, 42 (1): 51– 63, doi : 10.1016 / 0166-218X (93) 90178-Q.
• Клокс, Тон (1996), «Ширина круговых графиков по дереву», Int. J. Found. Comput. Sci., 7 (2): 111–120, doi : 10.1142 / S0129054196000099.
• Kloks, T.; Kratsch, D.; Вонг, CK (1998), «Минимальное заполнение на круговых и круговых графах», Journal of Algorithms, 28 (2): 272–289, doi : 10.1006 / jagm.1998.0936.
• Косточка А.В. (1988), «Верхние границы хроматического числа графов», Труды Института математики, 10 : 204–226, MR 0945704. Цит. По Агеев (1996).
• Косточка А.В.; Кратохвил, Дж. (1997), «Покрытие и раскраска полигонально-круговых графов», Дискретная математика, 163 (1–3): 299–305, doi : 10.1016 / S0012-365X (96) 00344-5.
• Нэш, Николас; Грегг, Дэвид (2010), «Чувствительный к выходу алгоритм для вычисления максимального независимого набора кругового графа», Письма об обработке информации, 116 (16): 630–634, doi : 10.1016 / j.ipl.2010.05.016, hdl : 10344/2228.
• Джереми Спинрад (1994), «Признание круговые графики ", Journal of Algorithms, 16 (2): 264–282, doi : 10.1006 / jagm.1994.1012.
• Тискин, Александр (2010)," Быстрое дистанционное умножение единичных матриц Монжа », Труды ACM-SIAM SODA 2010, стр. 1287–1296.
• Унгер, Вальтер (1988),« О k-раскраске круговых графов », STACS 88: 5th Ежегодный симпозиум по теоретическим аспектам компьютерных наук, Бордо, Франция, 11–13 февраля 1988 г., Proceedings, Lecture Notes in Computer Science, 294, Berlin: Springer, стр. 61–72, doi : 10.1007 / BFb0035832.
• Унгер, Уолтер (1992), «Сложность раскраски круговых графов», STACS 92: 9-й ежегодный симпозиум по теоретическим аспектам информатики, Кашан, Франция, 13–15 февраля 1992 г., Proceedings, Lecture Notes in Computer Science, 577, Berlin: Springer, pp. 389–400, doi : 10.1007 / 3- 540-55210-3_199.
• Wessel, W.; Pöschel, R. (1985), «О круговых графах», в Sachs, Horst (ed.), Graphs, Hypergraphs and Applications: Proceedings of the Conference on Graph Theory, проходившей в Eyba с 1 по 5 октября., 1984, Teubner-Texte zur Mathematik, 73, BG Teubner, стр. 207–210. Как цитирует Унгер (1988).

• Круговой график