Масштаб (карта)

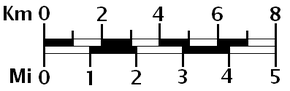
Отношение расстояния на карте к соответствующему расстоянию на земле Графическая или линейчатая шкала. На карте обычно указывается масштаб в числовом виде (например, «1: 50 000» означает, что один сантиметр на карте представляет 50 000 см реального пространства, что составляет 500 метров) Шкала шкалы с номинальным масштабом, выраженным как «1 см = 6 км »и« 1: 600 000 »(эквивалент, потому что 6 км = 600 000 см)

Масштаб карты - это соотношение расстояния на карте до расстояния на земле. Эта простая концепция усложняется из-за кривизны поверхности Земли, что приводит к изменению масштаба на карте. Из-за этого понятия приобретает смысл разными способами.

Первый способ - это отношение размера генерирующего глобуса к размеру Земли. Генерирующий глобус - это концептуальная модель, в соответствии с которой Земля сжата и на которую проецируется карта . Отношение размера Земли к размеру формирующегося земного шара называется номинальным масштабом (= ​​основным масштабом = репрезентативной долей ). На многих картах указан номинальный масштаб и может даже просто шкала (иногда «масштаб») для его представления.

Второе отличное понятие масштаба относится к варим масштаба на карте. Это отношение шкалы нанесенной точки к номинальной шкале. В данном случае «масштаб» означает масштабный коэффициент (= ​​точечная шкала = конкретный масштаб ).

Если область карты достаточно мала, чтобы игнорировать кривизну Земли, например, в качестве масштаба можно использовать одно значение, не вызывая ошибок измерения. На картах, покрывающих большие территории или Землю, масштаб карты может быть менее полезным или бесполезным для измерения расстояний. Проекция карты становится критически важной для понимания того, как масштабно меняется по всей карте. Изменяется масштабный коэффициент. Индикатриса Tissot часто используется для иллюстрации шкалы точек на карте.

Содержание

• 1 История
• 2 Терминология шкал
  • 2.1 Представление шкалы
  • 2.2 Гистограмма и лексическая шкала
  • 2.3 Крупномасштабная, средняя, ​​мелкая
  • 2.4 Изменение масштаба
• 3 Крупномасштабные карты без учета кривизны
• 4 Уменьшение высоты
• 5 Балльная шкала (или конкретный масштаб)
  • 5.1 Репрезентативная доля (RF) или основная шкала
  • 5.2 Визуализация точки шкала: индикатриса Тиссо
  • 5.3 Точечная шкала для нормальных цилиндрических проекций сферы
  • 5.4 Три примера нормальной цилиндрической проекции
    • 5.4.1 Равнопрямоугольная проекция
    • 5.4.2 Проекция Меркатора
    • 5.4. 3 Равноплоскостная проекция Ламберта
    • 5.4.4 Графики масштабных коэффициентов
  • 5.5 Изменение масштаба проекции Меркатора
  • 5.6 Секущие или модифицированные проекции
  • 5.7 Математическое приложение
• 6 Символ отношения
• 7 См.
• 8 Ссылки

История

Основы Также количественного масштабирования карты восходят к древнему Китаю с текстовыми свидетельствами что идея масштабирования карты была понята во втором веке нашей эры. Древние китайские геодезисты и картографы обладали обширными техническими средствами, которые использовались для производства карт, таких как счетные стержни, плотницкий квадрат, отвес, компасы для рисования кругов и визирных тубусов для измерения наклона. Системы отсчета, постулирующие или зарождающуюся систему координат для определения местоположения, были намекаются древними китайскими астрономами, которые обеспечивают различные сектора лунные ложи.

Китайский картограф и географ Пэй Сю из Трех Королевств. период создал набор карт большой площади, которые были нарисованы в масштабе. Он разработал набор принципов, в которых используется согласованное масштабирование измерений и корректировок в измерении земли на местности, которая была выполнена на карте.

Терминология масштабов

Представление масштаба

Масштаб карты может быть выражен словами (лексическая шкала), в виде отношений или дроби. Примеры:

«от одного сантиметра до ста метров» или 1:10 000 или 1/10 000

«от одного дюйма до одной мили» или 1: 63 360 или 1/63 360

»один сантиметр на тысячу километров, или 1: 100000000, или 1/100000000. (Соотношение обычно сокращается до 1: 100M)

Гистограмма и лексическая шкала

В дополнение к вышеперечисленному многие карты содержат одну или несколько (графических) линейных шкал. Например, на некоторых современных британских картах есть три шкалы шкалы, по одним километрам, миль и морских миль.

Лексическую шкалу на языке, известном пользователю, может быть легче визуализировать, чем соотношение: если масштаб составляет от дюйма до двух миль и пользователь карты. две деревни, которые находятся на расстоянии около двух дюймов друг от друга, то легко вычислить, что на земле эти деревни находятся на расстоянии около четырех миль друг от друга.

A лексическая шкала может вызвать проблемы, если она выражена на языке, который пользователь не понимает, или в устаревших или плохо определенныхах. Например, масштаб от одного дюйма до фарлонга (1: 7920) будет понятен многим пожилым людям в странах, где имперские единицы раньше преподавались в школах. Но масштаб от одного пула до одной лиги может составлять примерно 1: 144000, в зависимости от выбора картографом из множества различных определений лиги, и только меньшинство современных пользователей знакомы с используемыми модулями.

Крупномасштабный, средний, мелкий

Контрастность пространственного масштаба.

Карта классифицируется как мелкий масштаб или крупный масштаб или иногда средний масштаб . Малый масштаб относится к картам мира или картам больших регионов, таких как континенты или большие страны. Другими словами, они показывают большие участки земли на небольшом пространстве. Они называются мелкомасштабными, потому что репрезентативная фракция относительно мала.

Крупномасштабные карты показывают более мелкие области более подробно, например, карты округов или планы городов. Такие карты называются крупномасштабными, потому что репрезентативная доля относительно велика. Например, план города, представляет собой крупномасштабную карту, может иметь масштаб 1:10 000, тогда как карта мира представляет собой карту малого масштаба, может иметь масштаб 1: 100 000 000.

диапазоны для этих шкал, но ее следует рассматривать как авторитетные, поскольку нет стандартов:

Классификация	Диапазон	Примеры
крупномасштабный	1: 0 - 1 : 600,000	1: 0,00001 для карты вируса; 1: 5,000 для пешеходной карты города
среднего масштаба	1: 600,000 - 1: 2,000,000	Карта страны
малого масштаба	1: 2,000,000 - 1: ∞	1: 50,000,000 для карты мира; 1:10 для карты галактики

Термины иногда используются в абсолютном смысле источников, но иногда в относительном смысле. Например, картограф, чья работа относится исключительно к крупномасштабным картам (как указано в таблице выше), может называть карту размером 1: 500 000 мелкомасштабной.

На английском языке слово крупномасштабное часто используется для обозначения «обширного». Однако, как показано выше, картографы используют «крупномасштабные» для обозначения менее крупных карт - тех, которые показывают меньшую площадь. Карты, показывающие обширную территорию, используемые картами «малого масштаба». Это может вызвать недоумение.

Изменение масштаба

Нанесение на карту больших площадей вызывает заметные искажения, поскольку оно значительно выравнивает искривленную поверхность земли. Распределение искажений зависит от проекции карты . Масштабируется в зависимости от карты, и может быть карты лишь приблизительным. Это подробно обсуждается ниже.

Крупномасштабные карты без учета кривизны

Область, над которой Земля может считаться плоской, зависит от точности измерений обзора. Если измерять только с точностью до ближайшего метра, то кривизна Земли не может быть обнаружена на меридиональном расстоянии около 100 километров (62 мили) и на линии восток-запад около 80 км (на широта 45 градусов). При съемке с точностью до 1 миллиметра (0,039 дюйма) кривизна не обнаруживается на расстоянии меридиана около 10 км и на линии восток-запад около 8 км. Таким образом, план Нью-Йорка с точностью до одного метра или планочной площадки с точностью до одного миллиметра удовлетворяли бы указанные условия для пренебрежения кривизной. Их можно рассматривать с помощью съемки на плоскости и наносить на карту с помощью масштабных чертежей, на которых любые две точки на одинаковом расстоянии на чертеже находятся на одинаковом расстоянии на земле. Истинные расстояния до земли рассчитываются путем измерения расстояния на карте и последующего умножения на , обратное дробной части масштаба, что то же самое, просто с использованием разделителей для переноса расстояния между точками на карте в шкала штриха на карте.

Снижение высоты

Изменение высоты от уровня земли до поверхности сферы или эллипсоида также изменяет масштаб измерения расстояния.

Точечная шкала (или особенно масштаб)

Как доказано Гауссом Теоремой Эгрегиум, сферу (или эллипсоид) нельзя спроецировать на плоскость без искажения. Обычно это отображается невозможностью разглаживать апельсиновую корку на плоской поверхности, не деформируя ее. Единственное верное представление сферы в постоянном масштабе - это другая сфера, такая как глобус.

. Учитывая ограниченный практический размер глобусов, мы должны использовать карты для детального картирования. Карты требуют проекций. Проекция подразумевает: постоянное разделение на карте не соответствует постоянному разделу на земле. Хотя карта может отображать графическую шкалу, ее следует использовать с пониманием того, что она будет точной только на некоторых линиях карты. (Это обсуждается далее в примерах в следующих разделах.)

Пусть точка будет на широте $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$и долготе $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\; \}$на сфере (или эллипсоиде ). Пусть Q будет соседней точкой и пусть $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$будет углом между элементом PQ и меридианом в точке P: этот угол является азимутальным углом элемента PQ. Пусть P 'и Q' - соответствующие точки на проекции. Угол между направлением P'Q 'и проекцией меридиана равенство подшипнику$\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$. Обычно $\alpha \; \ne \; \beta \; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; neq\; \backslash \; beta\}$. Комментарий: это точное различие между азимутом (на поверхности Земли) и пеленгом (на карте) наблюдается не повсеместно, многие используют эти термины как синонимы.

Определение: шкала в точке P - это отношение двух расстояний P'Q 'и PQ в пределе, когда Q приближается к P. Мы записываем это как

$\mu \; (\lambda ,\; \phi ,\; \alpha )\; знак\; равно\; lim\; Q\; \to \; PP\; \prime \; Q\; \prime \; PQ,\; \{\backslash \; displaystyle\; \backslash \; mu\; (\backslash \; lambda,\; \backslash ,\; \backslash \; varphi,\; \backslash ,\; \backslash \; alpha)\; =\; \backslash \; lim\; \_\; \{Q\; \backslash \; to\; P\}\; \{\backslash \; frac\; \{P\; \text{'}Q\; \text{'}\}\; \{PQ\}\},\}$

где обозначение указывает, что шкала в пунктах является функцией положения P, а также направления элемента PQ.

Определение: если P и Q лежат на одном меридиане $(\alpha \; =\; 0)\; \{\backslash \; displaystyle\; (\backslash \; alpha\; =\; 0)\}$, шкала меридиана обозначается $час\; (\lambda ,\; \phi )\; \{\backslash \; displaystyle\; h\; (\backslash \; lambda,\; \backslash ,\; \backslash \; varphi)\}$.

Определение:, если P и Q лежат на одной параллели $(\alpha \; =\; \pi \; /\; 2)\; \{\backslash \; displaystyle\; (\backslash \; alpha\; =\; \backslash \; pi\; /\; 2)\}$, параллельная шкала обозначается $k\; (\lambda ,\; \phi )\; \{\backslash \; displaystyle\; k\; (\backslash \; lambda,\; \backslash ,\; \backslash \; varphi)\}$.

Определение: если шкала точек зависит только от положения, а не от направления, мы говорим, что она изотропна и условно обозначаем ее значение в любом направлении параллельным масштабным коэффициентом $k\; (\lambda ,\; \phi )\; \{\backslash \; displaystyle\; k\; (\backslash \; lambda,\; \backslash \; varphi)\}$.

Определение: Картографическая проекция называется конформной, если Угол между парой прямой, пересекающейся в точке P, такой же, как угол между проектируемыми линиями в спроецированной точке P 'для всех пар линий, пересекающихся в точке P. Конформная карта имеет изотропный масштабный коэффициент. И наоборот, изотропные масштабные коэффициенты на карте подразумевают конформную проекцию.

Изотропия элементы подразумевает, что маленькие растягиваются одинаково во всех направлениях, то есть форма маленького элемента сохраняется. Это свойство ортоморфизма (от греч. «Правильная форма»). Квалификация «малая» означает, что при некоторой заданной точности измерения не может быть обнаружено никаких изменений масштабного коэффициента по элементу. Конформные проекции имеют изотропный масштабный коэффициент, их также называют ортоморфными проекциями . Например, проекция Меркатора является конформной, поскольку она построена для сохранения угла, а ее масштабный коэффициент является изотопической функцией только широты: Меркатор действительно поддерживает форму в небольших регионах.

Определение: на конформной проекции с изотропным масштабом точки, которые могут быть объединены для образования линии изомасштаба . Они не являются стандартными картах для конечных пользователей. (См. Страницы Snyder 203–206.)

Репрезентативная дробь (RF) или основная шкала

При составлении уравнения любой данной проекции используются два соглашения. Например, равнопрямоугольная цилиндрическая проекция может быть записана как

картографы: $x\; =\; a\; \lambda \; \{\backslash \; displaystyle\; x\; =\; a\; \backslash \; lambda\}$$y\; =\; a\; \phi \; \{\backslash \; displaystyle\; y\; =\; a\; \backslash \; varphi\}$

математики : $x\; =\; \lambda \; \{\backslash \; displaystyle\; x\; =\; \backslash \; lambda\}$$y\; =\; \phi \; \{\backslash \; displaystyle\; y\; =\; \backslash \; varphi\}$

Здесь мы примем первое из этих соглашений (следуя использования в обзоре Снайдера). Очевидно, что приведенные выше уравнения проекции определяют положение огромного цилиндра, обернутого вокруг Земли и затем развернутого. Мы говорим, что эти координаты определяют карту, которую необходимо логически отличить от фактических напечатанных (или просматриваемых) карт. Если определение балльной шкалы в предыдущем разделе дано в терминах карты проекции, то можно ожидать, что масштабные коэффициенты будут близки к единице. Для нормальных касательных цилиндрических проекций вдоль экватора равенство k = 1, и в масштаб изменяется по мере удаления от экватора. Анализ масштаба на карте проекции - это исследование изменения k от его истинного значения единицы.

Фактические печатные карты последовательности из карты проекции постоянного масштабирования, обозначаемого обозначаемого, например 1: 100M (для карт всего мира) или 1: 10000 (для таких как планы городов)). Чтобы избежать путаницы при использовании слова «масштаб», эта доля мирового масштаба называется репрезентативной дробью (РФ) печатной карты, и ее следует идентифицировать с использованием напечатанным на карте. Фактические координаты напечатанной карты для равнопрямоугольной цилиндрической проекции:

печатная карта: $x\; =\; (RF)\; a\; \lambda \; \{\backslash \; displaystyle\; x\; =\; (RF)\; a\; \backslash \; lambda\}$$y\; =\; (RF)\; a\; \phi \; \{\backslash \; displaystyle\; y\; =\; (RF)\; a\; \backslash \; varphi\}$

Это соглашение позволяет четко различать собственное масштабирование проекции и уменьшение масштабирования.

С этого момента мы игнорируем РФ и работаем с картой проекции.

Визуализация точечной шкалы: индикатриса Тиссо

Треугольная проекция Винкеля с индикатрисой деформации Тиссо

Рассмотрим небольшой круг на поверхности Земли с центром в точке P на широте $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$и долготе $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$. Диаграмма круга на проекции будет искажена. Компания Tissot доказала, что до тех пор, пока искажение не слишком велико, круг на проекции превратится в эллипс. Обычно размер, форма и ориентация эллипса изменяются в зависимости от проекции. Наложение этих эллипсов искажения на проекцию карты передает способ изменения шкалы точек на карте. Эллипс искажения известен как индикатриса Тиссо. Показанный здесь пример - это тройная проекция Винкеля, стандартная проекция для карт мира, созданная Национальным географическим обществом. Минимальные искажения наблюдаются на центральном меридиане на 30 градусах широты (северная и южная). (Другие примеры).

Точечная шкала для нормальных цилиндрических проекций сферы

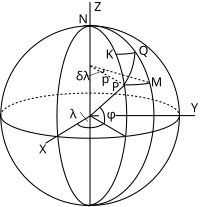
Ключом к количественному пониманию масштаба рассмотрение бесконечно малого элемента на сфере. На рисунке точка P на сфере с широтой $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$и долготой $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$. Точка Q находится на широте $\phi \; +\; \delta \; \phi \; \{\backslash \; displaystyle\; \backslash \; varphi\; +\; \backslash \; delta\; \backslash \; varphi\}$и долготе $\lambda \; +\; \delta \; \lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\; +\; \backslash \; delta\; \backslash \; lambda\}.$. Линии PK и MQ представляют собой дугами меридианов длиной $a\; \delta \; \phi \; \{\backslash \; displaystyle\; a\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\}$где $a\; \{\backslash \; displaystyle\; a\}$- радиус сферы, а $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$- в радианах. Прямые PM и KQ представляют собой дуги параллельных длин длиной $(a\; cos\; \; \phi )\; \delta \; \lambda \; \{\backslash \; displaystyle\; (a\; \backslash \; cos\; \backslash \; varphi)\; \backslash \; delta\; \backslash \; lambda\}$с $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$в радианах. При выводе точечного свойства проекции в P достаточно взять бесконечно малый элемент PMQK поверхности: в пределе Q, приближающемся к P, такой элемент стремится к бесконечно малому плоскому прямоугольнику.

Бесконечно малые элементы на сфере и нормальная цилиндрическая проекция

Нормальные цилиндрические проекции сферы имеют $x\; =\; a\; \lambda \; \{\backslash \; displaystyle\; x\; =\; a\; \backslash \; lambda\}$и $y\; \{\backslash \; displaystyle\; y\}$равно только функции широты. Следовательно, бесконечно малый элемент PMQK на сфере проецируется на бесконечно малый элемент P'M'Q'K ', который представляет собой точный прямоугольник с основанием $\delta \; x\; =\; a\; \delta \; \lambda \; \{\backslash \; displaystyle\; \backslash \; delta\; x\; =\; a\; \backslash ,\; \backslash \; дельта\; \backslash \; лямбда\}$и высота $\delta \; y\; \{\backslash \; displaystyle\; \backslash \; delta\; y\}$. Сравнивая элементы на сфере и проекции, мы можем сразу вывести выражения для масштабных коэффициентов на параллелях и меридианах. (Обработка масштаба в общем направлении может быть найдена ниже.)

параллельный масштабный коэффициент $k\; =\; \delta \; xa\; cos\; \; \phi \; \delta \; \lambda \; =\; sec\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; quad\; k\; \backslash \; ;\; =\; \backslash ;\; \{\backslash \; dfrac\; \{\backslash \; delta\; x\}\; \{a\; \backslash \; cos\; \backslash \; varphi\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\; \backslash ,\}\}\; =\; \backslash ,\; \backslash \; sec\; \backslash \; varphi\; \backslash \; qquad\; \backslash \; qquad\; \{\}\}$

масштабный коэффициент меридиана $час\; знак\; равно\; \delta \; Я.\; \delta \; \phi \; знак\; равно\; Y\; \prime \; (\phi )\; a\; \{\backslash \; displaystyle\; \backslash \; quad\; h\; \backslash ;\; =\; \backslash ;\; \{\backslash \; dfrac\; \{\backslash \; delta\; y\}\; \{a\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\; \backslash ,\}\}\; =\; \{\backslash \; dfrac\; \{\; y\; \text{'}(\backslash \; varphi)\}\; \{a\}\}\}$

Обратите внимание, что параллельный масштабный коэффициент $k\; =\; sec\; \; \phi \; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; \backslash \; varphi\}$не зависит от определения из $y\; (\phi )\; \{\backslash \; displaystyle\; y\; (\backslash \; varphi)\}$, поэтому он одинаков для всех нормальных цилиндрических проекций. Полезно отметить, что

на широте 30 градусов параллельный масштаб равен $k\; =\; sec\; \; 30\; \circ \; =\; 2/3\; =\; 1.15\; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; 30\; ^\; \{\backslash \; circ\}\; =\; 2\; /\; \{\backslash \; sqrt\; \{3\}\}\; =\; 1,15\}$

на широте 45 градусов параллельный масштаб равен $k\; =\; sec\; \; 45\; \circ \; =\; 2\; =\; 1,414\; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; 45\; ^\; \{\backslash \; circ\}\; =\; \{\backslash \; sqrt\; \{\; 2\}\}\; =\; 1.414\}$

на 60 градусах широты параллельный масштаб равен $k\; =\; sec\; \; 60\; \circ \; =\; 2\; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; 60\; ^\; \{\backslash \; circ\}\; =\; 2\}$

на 80 широте градусов, параллельный масштаб равен $k\; =\; sec\; \; 80\; \circ \; =\; 5.76\; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; 80\; ^\; \{\backslash \; circ\}\; =\; 5.76\}$

на широте 85 градусов параллельныймасштаб равенства $k\; =\; sec\; \; 85\; \circ \; =\; 11,5\; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; 85\; ^\; \{\backslash \; circ\}\; =\; 11,5\}$

Следующие примеры иллюстрируют три нормальных цилиндрических проекции, и в каждом случае изменение масштаба с положением и направлением изображения использованием Индикатриса Тиссо.

Три примера нормальной цилиндрической проекции

Равнопрямоугольная проекция

Квидистантная проекция с индикатрисой Тиссо деформации

равнопрямоугольная проекция, также известная как Plate Carrée (по-английски «плоский квадрат») или (что несколько вводит в заблуждение) эквидистантная проекция, определяется как

$x\; =\; a\; \lambda ,\; \{\backslash \; displaystyle\; x\; =\; a\; \backslash \; lambda,\; \}$$y\; =\; a\; \phi ,\; \{\backslash \; displaystyle\; y\; =\; a\; \backslash \; varphi,\}$

где $a\; \{\backslash \; displaystyle\; a\}$- это радиус сферы, $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$- долгота от центрального меридиана проекции (здесь принимается за гринвичский меридиан в $\lambda \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; 0\}$) и $\phi \; \{\backslash displaystyle\; \backslash \; varphi\}$- широта. Обратите внимание, что $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$и $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$выражены в радианах (получаются путем умножения степени на коэффициент $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$/ 180). Долгота $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$находится в диапазоне $[-\; \pi ,\; \pi ]\; \{\backslash \; displaystyle\; [-\; \backslash \; pi,\; \backslash \; pi]\}$и широта $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$находится в диапазоне $[-\; \pi \; /\; 2,\; \pi \; /\; 2]\; \{\backslash \; displaystyle\; [-\; \backslash \; pi\; /\; 2,\; \backslash \; pi\; /\; 2]\}$.

$y\; \prime \; (\phi )\; =\; 1\; \{\backslash \; displaystyle\; y\; \text{'}(\backslash \; varphi)\; =\; 1\}$, в предыдущем разделе дан

параллельный масштаб, $k\; =\; \delta \; xa\; соз\; \; \phi \; \delta \; \lambda \; знак\; равно\; сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; quad\; k\; \backslash ;\; знак\; равно\; \{\backslash \; dfrac\; \{\backslash \; delta\; x\}\; \{a\; \backslash \; cos\; \backslash \; varphi\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\; \backslash ,\}\}\; =\; \backslash ,\; \backslash \; sec\; \backslash \; varphi\; \backslash \; qquad\; \backslash \; qquad\; \{\}\}$

шкала меридиана $h\; =\; \delta \; ya\; \delta \; \phi \; знак\; равно\; 1\; \{\backslash \; Displaystyle\; \backslash \; четырехъядерный\; час\; \backslash ;\; знак\; равно\; \{\backslash \; dfrac\; \{\backslash \; delta\; y\}\; \{a\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\; \backslash ,\}\}\; =\; \backslash ,\; 1\}$

Для расчета шкалы в произвольном направлении см. приложение.

На рисунке индикатриса Tissot для этой проекции. На экваторе h = k = 1 и круговые элементы не искажены на проекции. На более высоких широтах круги искажаются, задаваемый вытягиванием только в параллельном направлении: в меридиональном направлении искажения нет. Отношение большой оси к малой оси составляет $сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$. Ясно, что площадь эллипса увеличивается во столько же раз.

Поучительно рассмотреть возможность использования линейчатых шкал, которые могут появиться в печатной версии этой проекции. Масштаб истинный (k = 1) на экваторе, так что умножение его на печатной карте на обратную вставку RF (или главный масштаб) дает фактическую длину окружности Земли. Шкала столбиков на карте также нарисована в истинном масштабе, поэтому перенос между двумя точками на экваторе на шкалу столбцов даст правильное расстояние между этими точками. То же самое и с меридианами. На параллели, отличной от экватора, масштаб составляет $сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$, поэтому, когда мы переносим разделение с параллели на шкалу столбцов, мы должны разделить расстояние шкалы столбцов с помощью этого коэффициента, чтобы получить расстояние между точками при измерении по параллели (которое не является истинным расстоянием по большому кругу). На линии с пеленгом, скажем, 45 градусов ($\beta \; =\; 45\; \circ \; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 45\; ^\; \{\backslash \; circ\}\}$) масштаб непрерывно изменяется с широтой и переносит разделение вдоль линии на шкале гистограммы не дает никакого отношения к истинному расстоянию. (Но см. приложение). Даже если бы мы могли вычислить расстояние по этой линии константы, ее актуальность сомнительна, поскольку такая линия на проекции соответствует сложной кривой на сфере. По этой причине линейчатую шкалу на мелкомасштабных картах следует использовать с особой осторожностью.

Проекция Меркатора

Проекция Меркатора с индикатрисой Тиссо деформации. (Искажение увеличенно увеличивается на более высоких широтах)

Проекция Меркатора отображает сферу в прямоугольник (бесконечной протяженности в $y\; \{\backslash \; displaystyle\; y\}$- направление) уравнениями

$Икс\; знак\; равно\; a\; \lambda \; \{\backslash \; Displaystyle\; х\; =\; а\; \backslash \; лямбда\; \backslash ,\}$

$у\; =\; а\; пер\; \; [загар\; \; (\pi \; 4\; +\; \phi \; 2)]\; \{\backslash \; Displaystyle\; у\; =\; а\; \backslash \; пер\; \backslash \; влево\; [\backslash \; загар\; \backslash \; влево\; (\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{4\}\}\; +\; \{\backslash \; frac\; \{\backslash \; varphi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right]\}$

где a, $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\; \backslash ,\}$и $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\; \backslash ,\}$такие же, как в предыдущем примере. $y\; \prime \; (\phi )\; =\; a\; sec\; \; \phi \; \{\backslash \; displaystyle\; y\; \text{'}(\backslash \; varphi)\; =\; a\; \backslash \; sec\; \backslash \; varphi\}$, коэффициенты масштабирования равны:

параллельному масштабу $k\; =\; \delta \; xa\; cos\; \; \phi \; \delta \; \lambda \; =\; sec\; \; \phi .\; \{\backslash \; Displaystyle\; к\; \backslash ;\; знак\; равно\; \{\backslash \; dfrac\; \{\backslash \; delta\; x\}\; \{a\; \backslash \; cos\; \backslash \; varphi\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\; \backslash ,\}\}\; =\; \backslash ,\; \backslash \; sec\; \backslash \; varphi.\}$

шкала меридианов $h\; =\; \delta \; ya\; \delta \; \phi \; =\; sec\; \phi .\; \{\backslash \; Displaystyle\; ч\; \backslash ;\; знак\; равно\; \{\backslash \; dfrac\; \{\backslash \; delta\; y\}\; \{a\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\; \backslash ,\}\}\; =\; \backslash ,\; \backslash \; sec\; \backslash \; varphi.\}$

В математическом приложении показано, что шкала точек в произвольном направлении также равна $сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$, шкала изотропна (одинакова во всех направлениях), величина ее увеличивается с широтой как $сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$. На диаграмме Тиссо каждый бесконечно малый круговой изменяет свою форму, но с увеличенной широты все больше и больше.

равновеликая проекция Ламберта

нормальная цилиндрическая равновеликая проекция Ламберта с индикатрисой Тиссо деформации

равновеликой проекцией Ламберта сфера отображается в конечный результат с помощью уравнений

$x\; =\; a\; \lambda \; y\; знак\; равно\; грех\; \; \phi \; \{\backslash \; displaystyle\; x\; =\; a\; \backslash \; lambda\; \backslash \; qquad\; \backslash \; qquad\; y\; =\; a\; \backslash \; sin\; \backslash \; varphi\}$

где a, $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$и $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$такие же, как в данном примере. $y\; \text{'}(\phi )\; =\; cos\; \; \phi \; \{\backslash \; displaystyle\; y\text{'}\; (\backslash \; varphi)\; =\; \backslash \; cos\; \backslash \; varphi\}$, масштабные коэффициенты равны

параллельному масштабу $k\; =\; \delta \; xa\; соз\; \; \phi \; \delta \; \lambda \; знак\; равно\; сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; quad\; k\; \backslash ;\; знак\; равно\; \{\backslash \; dfrac\; \{\backslash \; delta\; x\}\; \{a\; \backslash \; cos\; \backslash \; varphi\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\; \backslash ,\}\}\; =\; \backslash ,\; \backslash \; sec\; \backslash \; varphi\; \backslash \; qquad\; \backslash \; qquad\; \{\}\}$

шкала меридиана $h\; =\; \delta \; ya\; \delta \; \phi \; знак\; равно\; соз\; \; \phi \; \{\backslash \; Displaystyle\; \backslash \; четырехъядерный\; час\; \backslash ;\; знак\; равно\; \{\backslash \; dfrac\; \{\backslash \; delta\; y\}\; \{a\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\; \backslash ,\}\}\; =\; \backslash ,\; \backslash \; cos\; \backslash \; varphi\}$

Расчет балльной шкалы в произвольном направлении приведен ниже.

Вертикальная и горизонтальная шкалы теперь компенсируют друг друга (hk = 1), а на диаграмме Тиссо каждый бесконечно малый круговой искажен в эллипс той же площади, что и неискаженные круги на экваторе.

Графики масштабных коэффициентов

На графике показано изменение масштабных коэффициентов для трех приведенных выше примеров. На верхнем графике функции функция изотропной шкалы Меркатора: масштаб на параллели такой же, как и на шкалы меридиана. На других графиках показан масштабный коэффициент меридиана для равнопрямоугольной проекции (h = 1) и для равновеликой проекции Ламберта. Эти две проекции имеют параллельный масштаб, идентичный масштабную графику Меркатора. Что касается Ламберта, обратите внимание, что параллельный масштаб (как Меркатор A) увеличивается с широтой, масштаб меридиана (C) уменьшается с широтой таким образом, что hk = 1, что гарантирует сохранение площади.

Изменение масштаба проекции Меркатора

Шкала точек Меркатора равна единице на экваторе, потому что она такова, что вспомогательный цилиндр, используется в его конструкции, является касательной к Земле на экваторе. По этой причине обычную проекцию следует называть касательной проекцией. Масштаб изменяется в зависимости от широты как $k\; =\; sec\; \; \phi \; \{\backslash \; displaystyle\; k\; =\; \backslash \; sec\; \backslash \; varphi\}$. $sec\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$стремится к бесконечности по мере приближения к полюсам, карта Меркатора сильно искажается на высоких широтах, и по этой причине проекция совершенно не подходит для карт мира. (если мы не обсуждаем навигацию и румба ). Однако на широте около 25 градусов значение $сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$составляет около 1,1, поэтому точность Меркатора составляет 10% в полосе шириной 50 градусов. с центром на экваторе. Лучше использовать более узкие полосы: полоса шириной 16 градусов (с центром на экваторе) имеет точность в пределах 1% или 1 часть из 100.

Стандартный критерий для хороших крупномасштабных карт - точность должна быть в пределах 4 частей из 10 000, или 0,04%, что соответствует $k\; =\; 1.0004\; \{\backslash \; displaystyle\; k\; =\; 1.0004\}$. <Время $сек\; \; \phi \; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\}$достигает этого значения при $\phi \; =\; 1,62\; \{\backslash \; displaystyle\; \backslash \; varphi\; =\; 1,62\}$градусов (см. Рисунок ниже, Красная линия). Таким образом, касательная проекция Меркатора очень точна в пределах шириной 3,24 градуса с центром на экваторе. Это расстояние с севера на юг около 360 км (220 миль). Внутри этой полосы Меркатор очень хорош, очень точен и сохранен форму, потому что он конформный (центр города) угол. Эти наблюдения побудили к разработке поперечных проекций Меркатора, в которых мы получаем точную карту в пределах небольшого расстояния от этого меридиана. Такие карты подходят для стран, ориентированных почти с севера на юг (например, Великобритания ), и набор из 60 таких карт используется для универсальной поперечной проекции Меркатора (UTM). Обратите внимание, что в этих проекциях (которые основаны на различных эллипсоидах) уравнения преобразования для x и y и выражение для масштабного коэффициента используют сложные функции, такие как широты, так и долготы.

Изменение масштаба около экватора для касательной (красный) и секущей (зеленый) проекций Меркатора.

Секущие, или модифицированные, проекции

Основная идея проекции проекции заключается в том, что проекция сферы цилиндра, которая пересекает сферу в двух параллелях, скажем $\phi \; 1\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{1\}\; \}$север и юг. Ясно, что масштаб теперь верен на эти широт, тогда как параллели ниже этих широт сужаются проекцией, и их (параллельный) масштабный коэффициент должен быть меньше единицы. В результате отклонения шкалы от единицы в более широком диапазоне широт.

В примере одна возможная проекция секущей Меркатора определяется как

$x\; =\; 0,9996\; a\; \lambda \; y\; =\; 0,9996\; a\; ln\; \; (tan\; \; (\pi \; 4\; +\; \phi \; 2)).\; \{\backslash \; displaystyle\; x\; =\; 0,9996a\; \backslash \; lambda\; \backslash \; qquad\; \backslash \; qquad\; y\; =\; 0,9996a\; \backslash \; ln\; \backslash \; left\; (\backslash \; tan\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{4\}\}\; +\; \{\backslash \; frac\; \{\backslash \; varphi\}\; \{2\; \}\})\; \backslash \; right)\; \backslash \; right).\}$

Числовые множители не изменяют формуции, но это означает, что изменяются масштабные коэффициенты:

секущая шкала Меркатора, $k\; =\; 0,9996\; сек\; \; \phi .\; \{\backslash \; Displaystyle\; \backslash \; четырехъядерный\; к\; \backslash ;\; =\; 0,9996\; \backslash \; sec\; \backslash \; varphi.\}$

Таким образом,

• масштаб на экваторе равенство 0,9996,
• масштаб равен k = 1 на широте, заданной как $\phi \; 1\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{1\}\}$где $сек\; \; \phi \; 1\; =\; 1\; /\; 0,9996\; =\; 1,00004\; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\; \_\; \{1\}\; =\; 1\; /\; 0,9996\; =\; 1,00004\}$так, чтобы $\phi \; 1\; =\; 1,62\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{1\}\; =\; 1,62\}$градусов,
• k = 1.0004 в широта $\phi \; 2\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{2\}\}$, заданная как $сек\; \; \phi \; 2\; =\; 1.0004\; /\; 0.9996\; =\; 1.0008\; \{\backslash \; displaystyle\; \backslash \; sec\; \backslash \; varphi\; \_\; \{2\}\; =\; 1.0004\; /0.9996=\; 1.0008\}$, для которого $\phi \; 2\; =\; 2.29\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{2\}\; =\; 2.29\}$градусов. Следовательно, проекция имеет , то есть точность 0,04%, на более широкой полосе в 4,58 градуса (по сравнению с 3,24 градуса для касательной формы).

Это показано нижней (зеленой) кривой на рисунок из предыдущего раздела.

Такие узкие зоны высокой точности используются в UTM и британской проекции OSGB, обе из которых являются секущими, поперечными по Меркатору на эллипсоиде с масштабом постоянной центрального меридиана $k\; 0\; =\; 0,9996\; \{\backslash \; displaystyle\; k\_\; \{0\}\; =\; 0,9996\}$. Изомасштабные линии с $k\; =\; 1\; \{\backslash \; displaystyle\; k\; =\; 1\}$представляют собой слегка изогнутые линии примерно в 180 км к востоку и западу от центрального меридиана. Максимальное значение масштабного коэффициента составляет 1,001 для UTM и 1 0007 для OSGB.

Линии единичной шкалы на широте $\phi \; 1\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{1\}\}$(север и юг), где поверхность цилиндрической проекции пересекает сферу, являются стандартные параллели секущей проекции.

Пока узкая полоса с важен для высокоточного картографирования в крупном масштабе, для карт мира используются гораздо более широкие стандартные параллели, чтобы контролировать изменение масштаба. Примеры:

• Behrmann со стандартными параллелями на 30N, 30S.
• равная площадь Галла со стандартными параллелями на 45N, 45S.

Вариация шкалы для проекций равной площади Ламберта (зеленый) и Галла (красный)

Масштабные графики для последнего показаны ниже в сравнении с масштабными коэффициентами равной площади Ламберта. В последнем случае экватор представляет собой единую стандартную параллель, и параллельный масштаб увеличивается с k = 1, чтобы компенсировать уменьшение масштаба меридиана. Для Галла параллельный масштаб уменьшается на экваторе (до k = 0,707), в то время как масштаб меридиана увеличивается (до k = 1,414). Это приводит к грубому искажению формы в проекции Галла-Петерса. (На земном шаре длина Африки равна ширине). Обратите внимание, что шкала меридиана и параллели равны единице на стандартных параллелях.

Математическое приложение

Бесконечно малые элементы на сфере и нормальная цилиндрическая проекция

Для нормальных цилиндрических проекций геометрия бесконечно малых элементов дает

$(a)\; tan\; \; \alpha \; =\; a\; cos\; \; \phi \; \delta \; \lambda \; a\; \delta \; \phi ,\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{(a)\}\}\; \backslash \; quad\; \backslash \; tan\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{a\; \backslash \; cos\; \backslash \; varphi\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\}\; \{a\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\}\},\}$

$(б)\; tan\; \; \beta \; =\; \delta \; x\; \delta \; y\; =\; a\; \delta \; \lambda \; \delta \; y.\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{(b)\}\}\; \backslash \; quad\; \backslash \; tan\; \backslash \; beta\; =\; \{\backslash \; frac\; \{\backslash \; delta\; x\}\; \{\backslash \; delta\; y\}\}\; =\; \{\backslash \; frac\; \{a\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\}\; \{\backslash \; delta\; y\; \}\}.\}$

Отношение между углами $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$и $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$равно

$(\; в)\; tan\; \; \beta \; =\; a\; sec\; \; \phi \; y\; \prime \; (\phi )\; tan\; \; \alpha .\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{(c)\}\}\; \backslash \; quad\; \backslash \; tan\; \backslash \; beta\; =\; \{\backslash \; frac\; \{a\; \backslash \; sec\; \backslash \; varphi\}\; \{y\; \text{'}(\backslash \; varphi)\}\}\; \backslash \; tan\; \backslash \; alpha.\; \backslash ,\}$

Для проекции Меркатора $y\; \prime \; (\phi )\; =\; a\; sec\; \; \phi \; \{\backslash \; displaystyle\; y\; \text{'}(\backslash \; varphi)\; =\; a\; \backslash \; sec\; \backslash \; varphi\}$, что дает $\alpha \; =\; \beta \; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \backslash \; beta\}$: углы сохраняются. (Это не удивительно, поскольку это отношение используется для вывода Меркатора). Для эквидистантной проекции и проекции Ламберта имеем $y\; \prime \; (\phi )\; =\; a\; \{\backslash \; displaystyle\; y\; \text{'}(\backslash \; varphi)\; =\; a\}$и $y\; \prime \; (\phi )\; =\; a\; cos\; \; \phi \; \{\; \backslash \; displaystyle\; y\; \text{'}(\backslash \; varphi)\; =\; a\; \backslash \; cos\; \backslash \; varphi\}$, соответственно, поэтому связь между $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$и $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$зависит от широты $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$. Обозначим шкалу в P, когда бесконечно малый элемент PQ составляет угол $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash ,\}$с меридианом на $\mu \; \alpha .\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{\backslash \; alpha\}.\}$Он задается отношением расстояний:

$\mu \; \alpha \; =\; lim\; Q\; \to \; PP\; \prime \; Q\; \prime \; PQ\; =\; lim\; Q\; \to \; P\; \delta \; x\; 2\; +\; \delta \; y\; 2\; a\; 2\; \delta \; \phi \; 2\; +\; a\; 2\; соз\; 2\; \phi \; \delta \; \lambda \; 2.\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{\backslash \; alpha\}\; =\; \backslash \; lim\; \_\; \{Q\; \backslash \; to\; P\}\; \{\backslash \; frac\; \{P\text{'}Q\; \text{'}\}\; \{PQ\}\}\; =\; \backslash \; lim\; \_\; \{Q\; \backslash \; to\; P\}\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{\backslash \; delta\; x\; ^\; \{2\}\; +\; \backslash \; delta\; y\; ^\; \{2\}\}\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; \backslash ,\; \backslash \; delta\; \backslash \; varphi\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; varphi\; \backslash ,\; \backslash \; delta\; \backslash \; lambda\; ^\; \{2\}\}\}\}.\}$

Установка $\delta \; x\; =\; a\; \delta \; \lambda \; \{\backslash \; displ$