Конструкция Неймана

Конструкция Неймана - это частотный метод для построения интервала с уровнем достоверности $C,\; \{\backslash \; displaystyle\; C,\; \backslash ,\}$таким образом, что если мы повторим эксперимент много раз, интервал будет содержать истинное значение некоторого параметра в дробной части $C\; \{\backslash \; displaystyle\; C\; \backslash ,\}$времени. Он назван в честь Ежи Неймана.

• 1 Теория
• 2 Вероятность покрытия
• 3 Реализация
• 4 Классический пример
• 5 Другой пример
• 6 См. Также
• 7 Ссылки

Предположим $X\; 1,\; X\; 2,...\; X\; n\; \{\backslash \; displaystyle\; X\_\; \{1\},\; X\_\; \{2\},...\; X\_\; \{n\}\}$- случайные величины с объединенным pdf $f\; (x\; 1,\; x\; 2,...\; xn\; |\; \theta \; 1,\; \theta \; 2,...,\; \theta \; k)\; \{\backslash \; displaystyle\; f\; (x\_\; \{1\},\; x\_\; \{2\},...\; x\_\; \{n\}\; |\; \backslash \; theta\; \_\; \{1\},\; \backslash \; theta\; \_\; \{2\},...,\; \backslash \; theta\; \_\; \{k\})\}$, который зависит от k неизвестных параметров. Для удобства пусть $\Theta \; \{\backslash \; displaystyle\; \backslash \; Theta\}$будет пространством выборки, определяемым n случайными величинами, и затем определим точку выборки в пространстве выборки как $X\; =\; (X\; 1,\; X\; 2,...\; X\; n)\; \{\backslash \; displaystyle\; X\; =\; (X\_\; \{1\},\; X\_\; \{2\},...\; X\_\; \{n\})\}$. Нейман первоначально предложил определить две функции $L\; (x)\; \{\backslash \; displaystyle\; L\; (x)\}$и $U\; (x)\; \{\backslash \; displaystyle\; U\; (x)\}$так, что для любой точки выборки $X\; \{\backslash \; displaystyle\; X\}$,

• $L\; (X)\; \le \; U\; (X)\; \{\backslash \; displaystyle\; L\; (X)\; \backslash \; leq\; U\; (X)\}$$\forall \; X\; \in \; \Theta \; \{\backslash \; displaystyle\; \backslash \; forall\; X\; \backslash \; in\; \backslash \; Theta\}$
• L и U однозначны и определены.

Учитывая наблюдение, $X\; \prime \; \{\backslash \; displaystyle\; X\; ^\; \{\text{'}\}\}$, вероятность того, что $\theta \; 1\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\}$находится между $L\; (X\; \prime )\; \{\backslash \; displaystyle\; L\; (X\; ^\; \{\text{'}\})\}$и $U\; (X\; \prime )\; \{\backslash \; displaystyle\; U\; (X\; ^\; \{\text{'}\})\}$определяется как $P\; (L\; (X\; \prime )\; \le \; \theta \; 1\; \le \; U\; (X\; \prime )\; |\; X\; \prime )\; \{\backslash \; displaystyle\; P\; (L\; (X\; ^\; \{\text{'}\})\; \backslash \; leq\; \backslash \; theta\; \_\; \{1\}\; \backslash \; leq\; U\; (X\; ^\; \{\text{'}\})\; |\; X\; ^\; \{\text{'}\})\}$с вероятностью Только $0\; \{\backslash \; displaystyle\; 0\}$или $1\; \{\backslash \; displaystyle\; 1\}$. Эти вычисленные вероятности не позволяют сделать значимый вывод о $\theta \; 1\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\}$, поскольку вероятность равна нулю или единице. Кроме того, в соответствии с частотной конструкцией параметры модели являются неизвестными константами и не могут быть случайными величинами. Например, если $\theta \; 1\; =\; 5\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\; =\; 5\}$, то $P\; (2\; \le \; 5\; \le \; 10)\; =\; 1\; \{\backslash \; displaystyle\; P\; (2\; \backslash \; leq\; 5\; \backslash \; leq\; 10)\; =\; 1\}$. Аналогично, если $\theta \; 1\; =\; 11\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\; =\; 11\}$, то $P\; (2\; \le \; 11\; \le \; 10)\; =\; 0\; \{\backslash \; displaystyle\; P\; (2\; \backslash \; leq\; 11\; \backslash \; leq\; 10)\; =\; 0\}$

Как описывает Нейман в своей статье 1937 года, предположим, что мы рассматриваем все точки в пространстве выборки, то есть $\forall \; X\; \in \; \Theta \; \{\backslash \; displaystyle\; \backslash \; forall\; X\; \backslash \; in\; \backslash \; Theta\}$, которые представляют собой систему случайных величин, определяемую объединенным PDF-файлом, описанным выше. Поскольку $L\; \{\backslash \; displaystyle\; L\}$и $U\; \{\backslash \; displaystyle\; U\}$являются функциями $X\; \{\backslash \; displaystyle\; X\}$они тоже являются случайными величинами, и можно исследовать значение следующего утверждения вероятности:.

В рамках частотной конструкции параметры модели являются неизвестными константами и не могут быть случайными величинами. Рассматривая все точки выборки в пространстве выборки как случайные величины, определенные вышеупомянутым объединенным PDF-файлом, то есть все $X\; \in \; \Theta \; \{\backslash \; displaystyle\; X\; \backslash \; in\; \backslash \; Theta\}$можно показать, что $L\; \{\backslash \; displaystyle\; L\}$и $U\; \{\backslash \; displaystyle\; U\}$являются функциями случайных величин и, следовательно, случайных величин. Следовательно, можно посмотреть на вероятность $L\; (X)\; \{\backslash \; displaystyle\; L\; (X)\}$и $U\; (X)\; \{\backslash \; displaystyle\; U\; (X)\}$для некоторых $X\; \in \; \Theta \; \{\backslash \; displaystyle\; X\; \backslash \; in\; \backslash \; Theta\}$. Если $\theta \; 1\; \prime \; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\; ^\; \{\text{'}\}\}$- истинное значение $\theta \; 1\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\}$, мы можем определить $L\; \{\backslash \; displaystyle\; L\}$и $U\; \{\backslash \; displaystyle\; U\}$так, чтобы вероятность $L\; (X)\; \le \; \theta \; 1\; \prime \; \{\backslash \; displaystyle\; L\; (X)\; \backslash \; leq\; \backslash \; theta\; \_\; \{1\}\; ^\; \{\text{'}\}\}$и $\theta \; 1\; \prime \; \le \; U\; (X)\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\; ^\; \{\text{'}\}\; \backslash \; leq\; U\; (X)\}$равно предварительно заданному уровню достоверности $,\; C\; \{\backslash \; displaystyle,\; C\}$.

То есть $П\; (L\; (Икс)\; \le \; \theta \; 1\; \prime \; \le \; U\; (X)\; |\; \theta \; 1\; \prime )\; =\; С\; \{\backslash \; Displaystyle\; P\; (L\; (X)\; \backslash \; leq\; \backslash \; theta\; \_\; \{1\}\; ^\; \{\text{'}\}\; \backslash \; Leq\; U\; (X)\; |\; \backslash \; theta\; \_\; \{1\}\; ^\; \{\text{'}\})\; =\; C\}$где $0\; \le \; C\; \le \; 1\; \{\backslash \; displaystyle\; 0\; \backslash \; leq\; C\; \backslash \; leq\; 1\}$где $L\; (X)\; \{\backslash \; displaystyle\; L\; (X)\}$и $U\; (X)\; \{\backslash \; displaystyle\; U\; (X)\}$верхний и нижний доверительные границы для $\theta \; 1\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{1\}\}$

Вероятность охвата, $C\; \{\backslash \; displaystyle\; C\}$, для конструкции Неймана - частота расчетов Предполагается, что доверительный интервал содержит фактическое интересующее значение. Обычно вероятность охвата устанавливается равной $95\%\; \{\backslash \; displaystyle\; 95\; \backslash \%\}$достоверности. Для построения Неймана вероятность покрытия устанавливается равной некоторому значению $C\; \{\backslash \; displaystyle\; C\}$, где . Это значение $C\; \{\backslash \; displaystyle\; C\}$говорит о том, насколько уверенно истинное значение содержится в интервале.

Конструкция Неймана может быть выполнена путем выполнения нескольких экспериментов, которые создают наборы данных, соответствующие заданному значению параметра. Эксперименты проводятся с использованием традиционных методов, а пространство подобранных значений параметров составляет полосу, из которой может быть выбран доверительный интервал.

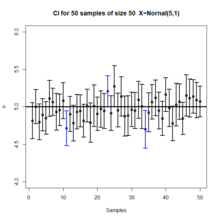
График 50 доверительных интервалов из 50 выборок, созданных из нормального распределения.

Предположим, $X\; \{\backslash \; displaystyle\; X\}$~$N\; (\theta ,\; \sigma \; 2)\; \{\backslash \; displaystyle\; N\; (\backslash \; theta,\; \backslash \; sigma\; ^\; \{2\})\}$, где $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$и $\sigma \; 2\; \{\backslash \; displaystyle\; \backslash \; sigma\; ^\; \{2\}\}$- неизвестные константы, для которых мы хотим оценить $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$. Мы можем определить (2) функции с одним значением, $L\; \{\backslash \; displaystyle\; L\}$и $U\; \{\backslash \; displaystyle\; U\}$, которые определены описанным выше процессом, так что заранее заданный уровень достоверности $C\; \{\backslash \; displaystyle\; C\}$и случайная выборка $X\; \ast \; \{\backslash \; displaystyle\; X\; ^\; \{*\}\}$=($x\; 1,\; x\; 2,...\; xn\; \{\backslash \; displaystyle\; x\_\; \{1\},\; x\_\; \{2\},...\; x\_\; \{n\}\}$)

$L\; (X\; \ast )\; =\; x\; ¯\; -\; tsn\; \{\backslash \; displaystyle\; L\; (X\; ^\; \{*\})\; =\; \{\backslash \; бар\; \{x\}\}\; -\; \{\backslash \; frac\; \{ts\}\; \{\backslash \; sqrt\; \{n\}\}\}\}$

$U\; (X\; \ast )\; =\; x\; ¯\; +\; tsn\; \{\backslash \; displaystyle\; U\; (X\; ^\; \{*\})\; =\; \{\backslash \; bar\; \{x\; \}\}\; +\; \{\backslash \; frac\; \{ts\}\; \{\backslash \; sqrt\; \{n\}\}\}\}$

где $x\; ¯\; =\; 1\; n\; \sum \; i\; =\; 1\; nxi\; =\; 1\; n\; (x\; 1,\; x\; 2,...\; xn)\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{x\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; x\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; (x\_\; \{1\},\; x\_\; \{2\},...\; x\_\; \{n\})\}$, $s\; =\; 1\; n\; -\; 1\; \sum \; i\; =\; 1\; n\; (xi\; -\; x\; ¯)\; 2\; \{\backslash \; displaystyle\; s\; =\; \{\backslash \; sqrt\; \{\{\backslash \; гидроразрыв\; \{1\}\; \{n-1\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; (x\_\; \{i\}\; -\; \{\backslash \; bar\; \{x\}\})\; ^\; \{2\}\}\}\}$

и $t\; \{\backslash \; displaystyle\; t\}$следует в распределении с (n-1) степенями свободы. $t\; \{\backslash \; displaystyle\; t\}$~t$(1\; -\; C\; /\; 2,\; n\; -\; 1)\; \{\backslash \; displaystyle\; (\{1-C\}\; /\; 2,\; n-1)\}$

$X\; 1,\; X\; 2,...,\; X\; n\; \{\backslash \; displaystyle\; X\_\; \{1\},\; X\_\; \{2\},...,\; X\_\; \{n\}\}$- случайные переменные iid, и пусть $T\; =\; (X\; 1,\; X\; 2,...,\; XZ\; n)\; \{\backslash \; displaystyle\; T\; =\; (X\_\; \{1\},\; X\_\; \{2\},...,\; XZ\_\; \{n\})\}$. Предположим, $T\; \sim \; N\; (\mu ,\; \sigma \; 2)\; \{\backslash \; displaystyle\; T\; \backslash \; sim\; N\; (\backslash \; mu,\; \backslash \; sigma\; ^\; \{2\})\}$. Теперь построим доверительный интервал с уровнем достоверности $C\; \{\backslash \; displaystyle\; C\}$. Мы знаем, что $x\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{x\}\}\}$достаточно для $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$. Итак,

$p\; (-\; Z\; \alpha \; 2\; \le \; x\; ¯\; -\; \mu \; \sigma \; 2\; \le \; Z\; \alpha \; 2)\; =\; C\; \{\backslash \; displaystyle\; p\; (-Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; leq\; \{\backslash \; frac\; \{\{\; \backslash \; bar\; \{x\}\}\; -\; \backslash \; mu\}\; \{\backslash \; sigma\; ^\; \{2\}\}\}\; \backslash \; leq\; Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\})\; =\; C\}$

$p\; (-\; Z\; \alpha \; 2\; \sigma \; 2\; \le \; x\; ¯\; -\; \mu \; \le \; Z\; \alpha \; 2\; \sigma \; 2)\; знак\; равно\; C\; \{\backslash \; displaystyle\; p\; (-Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\}\; \backslash \; leq\; \{\backslash \; bar\; \{x\}\}\; -\; \backslash \; mu\; \backslash \; leq\; Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\})\; =\; C\}$

$p\; (x\; ¯\; -\; Z\; \alpha \; 2\; \sigma \; 2\; \le \; \mu \; \le \; x\; ¯\; +\; Z\; \alpha \; 2\; \sigma \; 2)\; =\; C\; \{\; \backslash \; displaystyle\; p\; (\{\backslash \; bar\; \{x\}\}\; -\; Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\}\; \backslash \; leq\; \backslash \; mu\; \backslash \; leq\; \{\backslash \; bar\; \{x\}\}\; +\; Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\})\; =\; C\}$

Это дает $100\; (C)\%\; \{\backslash \; displaystyle\; 100\; (C)\; \backslash \%\}$доверительный интервал для $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$где,

$L\; (T)\; =\; x\; ¯\; -\; Z\; \alpha \; 2\; \sigma \; 2\; \{\backslash \; displaystyle\; L\; (T)\; =\; \{\backslash \; bar\; \{x\}\}\; -\; Z\_\; \{\backslash \; гидроразрыва\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\}\}$

$U\; (T)\; =\; x\; ¯\; +\; Z\; \alpha \; 2\; \sigma \; 2\; \{\backslash \; displaystyle\; U\; (T)\; =\; \{\backslash \; bar\; \{x\}\}\; +\; Z\; \_\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\}\}$.

• Вероятностные интерпретации