Войти
члены первого порядка (или поправки ) в математическом уравнении, выражении или модель - это термины с наибольшим порядком величины. Размеры различных членов в уравнении (ах) будут изменяться по мере изменения переменных, и, следовательно, какие члены в ведущем порядке также могут измениться.
Распространенный и эффективный способ упрощения и понимания большого количества сложных математических моделей - исследовать, какие термины являются наибольшими (и, следовательно, наиболее важными) для конкретных размеров переменных и параметров, и анализировать поведение производятся только этими терминами (остальные меньшие термины считаются незначительными). Это дает основное поведение - истинное поведение находится лишь в небольших отклонениях от него. Это основное поведение может быть достаточно хорошо отражено только терминами строго ведущего порядка, или может быть решено, что также следует включить несколько меньшие члены. В этом случае фраза в начальном порядке может использоваться неформально для обозначения всей этой группы терминов. Поведение, производимое только группой терминов ведущего порядка, называется поведением ведущего порядка модели.
| x | 0.001 | 0.1 | 0.5 | 2 | 10 |
|---|---|---|---|---|---|
| x | 0.000000001 | 0.001 | 0,125 | 8 | 1000 |
| 5x | 0,005 | 0,5 | 2,5 | 10 | 50 |
| 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| y | 0,105000001 | 0.601 | 2,725 | 18,1 | 1050,1 |
Рассмотрим уравнение y = x + 5x + 0,1. Для пяти различных значений x в таблице показаны размеры четырех членов в этом уравнении и какие члены являются ведущими. При дальнейшем увеличении x члены ведущего порядка остаются как x и y, но по мере того, как x уменьшается и затем становится все более и более отрицательным, какие члены ведущего порядка снова изменяются.
Не существует строгого ограничения для случаев, когда два члена должны или не должны рассматриваться как приблизительно один и тот же порядок или величина. Одно из возможных практических правил состоит в том, что два члена, которые находятся в пределах 10 (один порядок) друг от друга, должны рассматриваться как примерно одного порядка, а два члена, которые не находятся в пределах одного множителя. на 100 (два порядка) друг друга не должно. Однако между ними находится серая область, поэтому нет фиксированных границ, где термины следует рассматривать как приблизительно ведущие, а где нет. Вместо этого термины постепенно появляются и исчезают по мере изменения переменных. Решение о том, являются ли термины в модели ведущими (или приблизительно ведущими), а если нет, достаточно ли они малы, чтобы их можно было рассматривать как незначительные (два разных вопроса), часто является вопросом исследования и суждения, и будет зависят от контекста.
Уравнения только с одним членом ведущего порядка возможны, но редко. Например, уравнение 100 = 1 + 1 + 1 +... + 1 (где правая часть состоит из ста единиц). Для любой конкретной комбинации значений переменных и параметров уравнение обычно будет содержать по меньшей мере два члена старшего порядка и другие члены младшего порядка . В этом случае, делая предположение, что члены более низкого порядка и части членов высшего порядка, которые имеют тот же размер, что и члены более низкого порядка (возможно, вторая или третья значащая цифра и далее), пренебрежимо малы, новое уравнение можно сформировать, отбросив все эти члены более низкого порядка и части членов старшего порядка. Остальные члены образуют уравнение первого порядка, или баланс ведущего порядка, или доминирующий баланс, и создание нового уравнения, включающего только эти члены, известно как перевод уравнения в ведущий порядок. Решения этого нового уравнения называются решениями первого порядка исходного уравнения. Анализ поведения, задаваемого этим новым уравнением, дает поведение ведущего порядка модели для этих значений переменных и параметров. Размер ошибки при получении этого приближения обычно примерно равен размеру наибольшего игнорируемого члена.
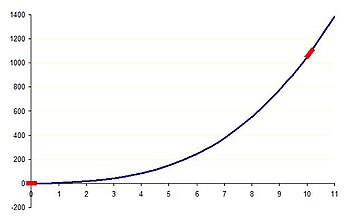y = x + 5x + 0,1. Ведущее или основное поведение при x = 0,001 - это постоянство y, а при x = 10 - кубическое увеличение y с увеличением x. Предположим, мы хотим понять поведение ведущего порядка в примере выше.
Таким образом, основное поведение y может быть исследовано при любом значении x. Поведение в ведущем порядке усложняется, когда в ведущем порядке больше терминов. При x = 2 существует баланс первого порядка между кубической и линейной зависимостями y от x.
Обратите внимание, что это описание поиска балансов и поведения ведущего порядка дает только общее описание процесса - оно не является математически строгим.
Конечно, y на самом деле не является полностью постоянным при x = 0,001 - это просто его основное поведение в окрестности этой точки. Может случиться так, что сохранение только членов первого порядка (или приблизительно ведущего порядка) и рассмотрение всех других более мелких членов как незначительных недостаточно (например, при использовании модели для будущего прогнозирования), и поэтому может потребоваться также сохранить набор следующих по величине условий. Их можно назвать условиями или исправлениями следующего за ведущим порядком (NLO). Следующий набор терминов после этого может называться условиями или поправками в порядке «следующий за следующим за ведущим» (NNLO).
Методы упрощения ведущего порядка используются вместе с методом согласованных асимптотических разложений, когда точное приближенное решение в каждой подобласти является решением ведущего порядка.
Для конкретных сценариев потока жидкости (очень общие) уравнения Навье – Стокса можно значительно упростить, рассматривая только компоненты старшего порядка. Например, уравнения потока Стокса. Кроме того, уравнения тонкой пленки теории смазки.
