Джет Ландау – Сквайра

В гидродинамике, Джет Ландау-Сквайра или Под водой Струя Ландау описывает затопленную круглую струю, исходящую от точечного источника импульса в бесконечную текучую среду того же типа. Это точное решение уравнений Навье-Стокса, которое впервые было открыто Львом Ландау в 1944 году, а затем Гербертом Сквайром в 1951 году. Фактически, автомодельное уравнение было первым. выведен Н. А. Слезкиным в 1934 г., но никогда не применялся к реактивному. Следуя работам Ландау, В.И. Яцеев получил общее решение уравнения в 1950 г.

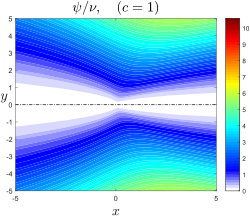
Линии тока струи Ландау-Сквайра для c = 0,01 Линии тока струи Ландау-Сквайра для c = 0,1 Линии тока струи Ландау-Сквайра для c = 1

Проблема описывается в сферических координатах $(r,\; \theta ,\; \varphi )\; \{\backslash \; displaystyle\; (r,\; \backslash \; theta,\; \backslash \; phi)\}$с компонентами скорости $(u,\; v,\; 0)\; \{\backslash \; displaystyle\; (u,\; v,\; 0)\}$. Поток осесимметричен, то есть не зависит от $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$. Тогда уравнение неразрывности и несжимаемая уравнения Навье – Стокса сводятся к

$1 r 2 ∂ ∂ r (r 2 u) + 1 r sin ⁡ θ ∂ ∂ θ (v sin ⁡ θ) = 0 u ∂ u ∂ r + vr ∂ u ∂ θ - v 2 r = - 1 ρ ∂ p ∂ r + ν (∇ 2 u - 2 ur 2-2 r 2 ∂ v ∂ θ - 2 v детская кроватка ⁡ θ r 2) u ∂ v ∂ r + vr ∂ v ∂ θ + uvr = - 1 ρ r ∂ p ∂ θ + ν (∇ 2 v + 2 r 2 ∂ u ∂ θ - vr 2 sin 2 ⁡ θ) {\ displaystyle {\ begin {выровнено} {\ frac {1} {r ^ {2}}} {\ frac {\ partial} {\ partial r}} (r ^ {2} u) + {\ frac {1} {r \ sin \ theta}} {\ frac {\ partial} {\ partial \ theta}} (v \ sin \ theta) = 0 \\ [8pt] u {\ frac {\ partial u} {\ partial r}} + {\ frac {v} {r}} {\ frac {\ partial u} {\ partial \ theta}} - {\ frac {v ^ {2}} {r}} = - {\ frac {1} {\ rho} } {\ frac {\ partial p} {\ partial r}} + \ nu \ left (\ nabla ^ {2} u - {\ frac {2u} {r ^ {2}}} - {\ frac {2} {r ^ {2}}} {\ frac {\ partial v} {\ partial \ theta}} - {\ frac {2v \ cot \ theta} {r ^ {2}}} \ right) \\ [8pt] u {\ frac {\ partial v} {\ partial r}} + {\ frac {v} {r}} {\ frac {\ partial v} {\ partial \ theta}} + {\ frac {uv} {r }} = - {\ frac {1} {\ rho r}} {\ frac {\ partial p} {\ partial \ the ta}} + \ nu \ left (\ nabla ^ {2} v + {\ frac {2} {r ^ {2}}} {\ frac {\ partial u} {\ partial \ theta}} - {\ frac { v} {r ^ {2} \ sin ^ {2} \ theta}} \ right) \ end {align}}}$

где

$\nabla \; 2\; =\; 1\; r\; 2\; \partial \; \partial \; r\; (r\; 2\; \partial \; \partial \; r)\; +\; 1\; г\; 2\; грех\; \; \theta \; \partial \; \partial \; \theta \; (грех\; \; \theta \; \partial \; \partial \; \theta ).\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; r\}\}\; \backslash \; left\; (r\; ^\; \{2\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; r\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\; \backslash \; sin\; \backslash \; theta\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; \backslash \; left\; (\backslash \; sin\; \backslash \; theta\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; \backslash \; right).\}$

Самоподобное описание решения доступно в следующей форме:

$u\; =\; \nu \; r\; sin\; \; \theta \; f\; \prime \; (\theta ),\; v\; =\; -\; \nu \; r\; sin\; \; \theta \; f\; (\theta ).\; \{\backslash \; displaystyle\; u\; =\; \{\backslash \; frac\; \{\backslash \; nu\}\; \{r\; \backslash \; sin\; \backslash \; theta\}\}\; f\; \text{'}(\backslash \; theta),\; \backslash \; quad\; v\; =\; -\; \{\backslash \; frac\; \{\backslash \; nu\}\; \{r\; \backslash \; sin\; \backslash \; theta\}\}\; f\; (\backslash \; theta).\}$

Подставив вышеуказанную автомодельную форму в основные уравнения и используя граничные условия $u\; =\; v\; =\; p\; -\; p\; \infty \; =\; 0\; \{\backslash \; displaystyle\; u\; =\; v\; =\; p-p\; \_\; \{\backslash \; infty\}\; =\; 0\}$на бесконечности, можно найти форму для давления как

$p\; -\; p\; \infty \; \rho \; =\; -\; v\; 2\; 2\; +\; \nu \; ur\; +\; c\; 1\; r\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{p-p\_\; \{\backslash \; infty\}\}\; \{\backslash \; rho\}\}\; =\; -\; \{\backslash \; frac\; \{v\; ^\; \{2\}\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{\backslash \; nu\; u\}\; \{r\}\}\; +\; \{\backslash \; frac\; \{c\_\; \{1\}\}\; \{\; r\; ^\; \{2\}\}\}\}$

где $c\; 1\; \{\backslash \; displaystyle\; c\_\; \{1\}\}$- константа. Используя это давление, мы снова находим из уравнения количества движения,

$-\; u\; 2\; r\; +\; vr\; \partial \; u\; \partial \; \theta \; =\; \nu \; r\; 2\; [2\; u\; +\; 1\; sin\; \; \theta \; \partial \; \partial \; \theta \; (sin\; \; \theta \; \partial \; u\; \partial \; \theta )]\; +\; 2\; в\; 1\; п\; 3.\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{u\; ^\; \{2\}\}\; \{r\}\}\; +\; \{\backslash \; frac\; \{v\}\; \{r\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; u\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; =\; \{\backslash \; frac\; \{\backslash \; nu\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; left\; [2u\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sin\; \backslash \; theta\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; \backslash \; left\; (\backslash \; sin\; \backslash \; theta\; \{\backslash \; frac\; \{\backslash \; partial\; u\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; \backslash \; right)\; \backslash \; right]\; +\; \{\backslash \; frac\; \{2c\_\; \{1\}\}\; \{r\; ^\; \{3\}\}\}.\}$

Замена $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$на $\mu \; =\; cos\; \; \theta \; \{\backslash \; displaystyle\; \backslash \; mu\; =\; \backslash \; cos\; \backslash \; theta\}$в качестве независимой переменной, скорости становятся

$u\; =\; -\; \nu \; rf\; \prime \; ({\rm M}),\; v\; =\; -\; \nu \; rf\; (\mu )\; 1\; -\; \mu \; 2\; \{\backslash \; displaystyle\; u\; =\; -\; \{\backslash \; frac\; \{\backslash \; nu\}\; \{r\}\}\; f\; \text{'}(\backslash \; mu),\; \backslash \; quad\; v\; =\; -\; \{\backslash \; frac\; \{\; \backslash \; nu\}\; \{r\}\}\; \{\backslash \; frac\; \{f\; (\backslash \; mu)\}\; \{\backslash \; sqrt\; \{1-\; \backslash \; mu\; ^\; \{2\}\}\}\}\}$

(для краткости тот же символ используется для $f\; (\theta )\; \{\backslash \; displaystyle\; f\; (\backslash \; theta)\}$и $f\; (\mu )\; \{\backslash \; displaystyle\; f\; (\backslash \; mu)\}$хотя функционально они одинаковы, но принимает разные числовые значения), и уравнение принимает вид

$f\; \prime \; 2\; +\; ff\; ″\; =\; 2\; f\; \prime \; +\; [(1\; -\; \mu \; 2)\; f\; ″]\; \prime \; -\; 2\; c\; 1.\; \{\backslash \; displaystyle\; f\; \text{'}^\; \{2\}\; +\; ff\text{'}\; \text{'}=\; 2f\text{'}\; +\; [(1-\; \backslash \; mu\; ^\; \{2\})\; f\; \text{'}\text{'}]\; \text{'}-\; 2c\_\; \{1\}.\}$

После двух интегрирований уравнение сокращается к

$е\; 2\; знак\; равно\; 4\; \mu \; е\; +\; 2\; (1\; -\; \mu \; 2)\; f\; \prime \; -\; 2\; (c\; 1\; \mu \; 2\; +\; c\; 2\; \mu \; +\; c\; 3),\; \{\backslash \; displaystyle\; f\; ^\; \{2\}\; =\; 4\; \backslash \; mu\; f\; +\; 2\; (1-\; \backslash \; mu\; ^\; \{2\})\; f\text{'}-2\; (c\_\; \{1\}\; \backslash \; mu\; ^\; \{2\}\; +\; c\_\; \{2\}\; \backslash \; mu\; +\; c\_\; \{3\}),\}$

где $c\; 2\; \{\backslash \; displaystyle\; c\_\; \{2\}\}$и $c\; 3\; \{\backslash \; displaystyle\; c\_\; \{3\}\}$- константы интегрирования. Вышеприведенное уравнение представляет собой уравнение Риккати. После некоторых вычислений общее решение может быть показано как

$f\; =\; \alpha \; (1\; +\; \mu )\; +\; \beta \; (1\; -\; \mu )\; +\; 2\; (1\; -\; \mu \; 2)\; (1\; +\; \mu )\; \beta \; (1\; -\; \mu )\; \alpha \; [с\; -\; \int \; 1\; \mu \; (1\; +\; \mu )\; \beta \; (1\; -\; \mu )\; \alpha ]\; -\; 1,\; \{\backslash \; displaystyle\; f\; =\; \backslash \; alpha\; (1+\; \backslash \; mu)\; +\; \backslash \; beta\; (1-\; \backslash \; mu)\; +\; \{\backslash \; frac\; \{2\; (1-\; \backslash \; mu\; ^\; \{2\})\; (1+\; \backslash \; mu)\; ^\; \{\backslash \; beta\}\}\; \{(1-\; \backslash \; mu)\; ^\; \{\backslash \; alpha\}\}\}\; \backslash \; left\; [c-\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; mu\}\; \{\backslash \; frac\; \{(1+\; \backslash \; mu)\; ^\; \{\backslash \; beta\}\}\; \{(1-\; \backslash \; mu)\; ^\; \{\backslash \; alpha\}\}\}\; \backslash \; right]\; ^\; \{-\; 1\},\}$

где $\alpha ,\; \beta ,\; c\; \{\backslash \; displaystyle\; \backslash \; alpha,\; \backslash \; \backslash \; beta,\; \backslash \; c\}$- константы. Физически релевантное решение для струи соответствует случаю $\alpha \; =\; \beta \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \backslash \; beta\; =\; 0\}$(эквивалентно, мы говорим, что $c\; 1\; =\; c\; 2\; =\; c\; 3\; =\; 0\; \{\backslash \; displaystyle\; c\_\; \{1\}\; =\; c\_\; \{2\}\; =\; c\_\; \{3\}\; =\; 0\}$, так что решение не имеет сингулярностей на оси симметрии, за исключением начала координат). Следовательно,

$f\; =\; 2\; (1\; -\; \mu \; 2)\; c\; +\; 1\; -\; \mu \; =\; 2\; sin\; 2\; \; \theta \; c\; +\; 1\; -\; cos\; \; \theta .\; \{\backslash \; displaystyle\; f\; =\; \{\backslash \; frac\; \{2\; (1-\; \backslash \; mu\; ^\; \{2\})\}\; \{c\; +\; 1-\; \backslash \; mu\}\}\; =\; \{\backslash \; frac\; \{2\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\; \{c\; +\; 1-\; \backslash \; cos\; \backslash \; theta\}\}.\}$

Функция $f\; \{\backslash \; displaystyle\; f\}$связана с функцией потока как $\psi \; =\; \nu \; rf\; \{\backslash \; displaystyle\; \backslash \; psi\; =\; \backslash \; nu\; rf\}$, таким образом, контуры $f\; \{\backslash \; displaystyle\; f\}$для разных значений $c\; \{\backslash \; displaystyle\; c\}$обеспечивает оптимизацию. Константа $c\; \{\backslash \; displaystyle\; c\}$описывает силу в начале координат, действующую в направлении струи (эта сила равна скорости передачи импульса через любую сферу вокруг начала координат плюс сила в направлении струи, создаваемой сферой из-за давления и сил вязкости), точное соотношение между силой и константой определяется выражением

$F\; 2\; \pi \; \nu \; 2\; =\; 32\; (c\; +\; 1)\; 3\; c\; (c\; +\; 2)\; +\; 8\; (c\; +\; 1)\; -\; 4\; (c\; +\; 1)\; 2\; ln\; \; c\; +\; 2\; c.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{F\}\; \{2\; \backslash \; pi\; \backslash \; nu\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{32\; (c\; +\; 1)\}\; \{3c\; (c\; +\; 2)\}\}\; +\; 8\; (c\; +\; 1)\; -\; 4\; (c\; +\; 1)\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; frac\; \{c\; +\; 2\}\; \{c\}\}.\}$

Решение описывает струю жидкости, быстро удаляющуюся от начала координат и увлекающую медленно движущуюся жидкость за пределы струя. Край струи можно определить как место, где линии тока находятся на минимальном расстоянии от оси, то есть e край задается как

$\theta \; o\; =\; cos\; -\; 1\; \; (1\; 1\; +\; c).\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{o\}\; =\; \backslash \; cos\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{1\; +\; c\}\}\; \backslash \; right).\}$

Следовательно, сила может быть выражена альтернативно, используя это полуугол конической границы струи,

$F\; 2\; \pi \; \nu \; 2\; =\; 32\; 3\; cos\; \; \theta \; o\; sin\; 2\; \; \theta \; o\; +\; 4\; cos\; \; \theta \; o\; ln\; \; 1\; -\; cos\; \; \theta \; o\; 1\; +\; cos\; \; \theta \; o\; +\; 8\; cos\; \; \theta \; o.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{F\}\; \{2\; \backslash \; pi\; \backslash \; nu\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{32\}\; \{3\}\}\; \{\backslash \; frac\; \{\backslash \; cos\; \backslash \; theta\; \_\; \{o\}\}\; \{\backslash \; sin\; ^\; \{\; 2\}\; \backslash \; theta\; \_\; \{o\}\}\}\; +\; \{\backslash \; frac\; \{4\}\; \{\backslash \; cos\; \backslash \; theta\; \_\; \{o\}\}\}\; \backslash \; ln\; \{\backslash \; frac\; \{1-\; \backslash \; cos\; \backslash \; theta\; \_\; \{o\}\}\; \{1+\; \backslash \; cos\; \backslash \; theta\; \_\; \{o\}\}\}\; +\; \{\backslash \; frac\; \{8\}\; \{\backslash \; cos\; \backslash \; theta\; \_\; \{o\}\}\}.\}$

Когда сила становится большой, полуугол струи становится малым, и в этом случае

$F\; 2\; \pi \; \nu \; 2\; \sim \; 32\; 3\; \theta \; o\; 2\; \ll \; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{F\}\; \{2\; \backslash \; pi\; \backslash \; nu\; ^\; \{2\}\}\}\; \backslash \; sim\; \{\backslash \; frac\; \{32\}\; \{3\; \backslash \; theta\; \_\; \{o\}\; ^\; \{2\}\}\}\; \backslash \; ll\; 1\}$

и решение внутри и снаружи струи принимает вид

В этом предельном случае струя называется струей Schlichting 88>. С другой стороны, когда сила мала,

$F\; 2\; \pi \; \nu \; 2\; \sim \; 8\; c\; \gg \; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{F\}\; \{2\; \backslash \; pi\; \backslash \; nu\; ^\; \{2\}\}\}\; \backslash \; sim\; \{\backslash \; frac\; \{8\}\; \{c\}\}\; \backslash \; gg\; 1\}$

полуугол приближается к 90 градусам (нет внутренней и внешней области, вся область рассматривается как одна область), само решение переходит к

$f\; (\theta )\; \sim \; 2\; c\; sin\; 2\; \; \theta .\; \{\backslash \; displaystyle\; f\; (\backslash \; theta)\; \backslash \; sim\; \{\backslash \; frac\; \{2\}\; \{c\}\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta.\}$

• Schlichting jet
• Schneider flow