В математике, концепция графических динамических систем может использоваться для захвата широкого спектра процессов, происходящих в графах или сетях. Основная тема математического и вычислительного анализа GDS состоит в том, чтобы связать их структурные свойства (например, возможность подключения к сети) и возникающую в результате глобальную динамику.
В работе над GDS рассматриваются конечные графы и пространства конечных состояний. Таким образом, исследование обычно включает методы, например, из теории графов, комбинаторики, алгебры и динамических систем, а не дифференциальной геометрии.. В принципе, можно определить и изучить GDS на бесконечном графе (например, клеточные автоматы или вероятностные клеточные автоматы на 

Графическая динамическая система состоит из следующих компонентов:
Фазовое пространство, ассоциированное с динамической системой с отображением F: K → K, представляет собой конечный ориентированный граф с множеством вершин K и ориентированными ребрами (x, F (x)). Структура фазового пространства определяется свойствами графа Y, вершинными функциями (f i)iи схемой обновления. Исследования в этой области направлены на то, чтобы вывести свойства фазового пространства на основе структуры компонентов системы. Анализ носит локально-глобальный характер.
Если, например, схема обновления состоит из синхронного применения вершинных функций, получается класс обобщенных клеточные автоматы (CA). В этом случае глобальное отображение F: K → K задается формулой
Этот класс называется обобщенными клеточными автоматами, поскольку классические или стандартные клеточные автоматы обычно определяются и изучаются над регулярными графами или сетками, и вершинные функции обычно считаются идентичными.
Пример: Пусть Y - круговой граф на вершинах {1,2,3,4} с ребрами {1,2}, {2,3}, {3,4} и {1,4}, обозначенные Circ. 4. Пусть K = {0,1} будет пространством состояний для каждой вершины и использовать функцию nor 3 : K → K, определенную формулой nor 3 (x, y, z) = ( 1 + x) (1 + y) (1 + z) с арифметикой по модулю 2 для всех вершинных функций. Затем, например, состояние системы (0,1,0,0) отображается в (0, 0, 0, 1) с использованием синхронного обновления. Все переходы показаны в фазовом пространстве ниже.
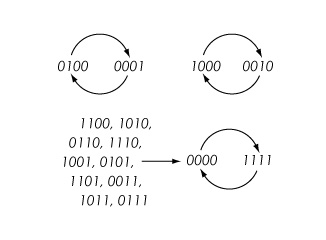 326
326 Если вершинные функции применяются асинхронно в последовательности, указанной словом w = (w 1, w 2,..., w m) или перестановка 


![F_ {i} (x) = (x_ {1}, x_ {2}, \ ldots, x _ {{i-1}}, f_ {i} (x [i]), x _ {{i + 1}}, \ ldots, x_ {n}) \ ;.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0297cda06442aa0a2bb3a1835cf94c5e8011fba)
Карта SDS F = [F Y, w]: K → K - это композиция функций
![[ F_ {Y}, w] = F _ {{w (m)}} \ circ F _ {{w (m-1)}} \ circ \ cdots \ circ F _ {{w (2)}} \ circ F _ {{ w (1)}} \ ;.](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca42ec3794afcdf858b2c72b17b1c5d18f8c90cc)
Если последовательность обновления представляет собой перестановку, часто говорят о SDS перестановки, чтобы подчеркнуть этот момент.
Пример: Пусть Y - круговой граф на вершинах {1,2,3,4} с ребрами {1,2}, {2,3}, {3,4} и {1,4}, обозначенный Circ 4. Пусть K = {0,1} будет пространством состояний для каждой вершины и использовать функцию nor 3 : K → K, определенную формулой nor 3 (x, y, z) = ( 1 + x) (1 + y) (1 + z) с арифметикой по модулю 2 для всех вершинных функций. Используя последовательность обновления (1,2,3,4), состояние системы (0, 1, 0, 0) отображается в (0, 0, 1, 0). Все переходы состояний системы для этой последовательной динамической системы показаны в фазовом пространстве ниже.
 326
326 Например, с точки зрения приложений интересно рассмотреть случай, когда один или несколько компонентов GDS содержат стохастические элементы. Мотивационные приложения могут включать в себя процессы, которые не до конца поняты (например, динамика внутри ячейки), и где определенные аспекты для всех практических целей, похоже, ведут себя в соответствии с некоторым распределением вероятностей. Существуют также приложения, управляемые детерминированными принципами, описание которых настолько сложно или громоздко, что имеет смысл рассматривать вероятностные приближения.
Каждый элемент графической динамической системы можно сделать стохастическим несколькими способами. Например, в последовательной динамической системе последовательность обновления может быть сделана стохастической. На каждом шаге итерации можно выбрать последовательность обновления w случайным образом из заданного распределения последовательностей обновления с соответствующими вероятностями. Соответствующее вероятностное пространство обновленных последовательностей порождает вероятностное пространство SDS-карт. Естественным объектом для изучения в этом отношении является цепь Маркова в пространстве состояний, индуцированная этим набором SDS-отображений. Этот случай упоминается как стохастический GDS последовательности обновления и мотивируется, например, процессами, в которых «события» происходят случайным образом в соответствии с определенными скоростями (например, химические реакции), синхронизацией в параллельных вычислениях / симуляциях дискретных событий и в вычислительных парадигмах, описанных ниже..
Этот конкретный пример со стохастической последовательностью обновления иллюстрирует два общих факта для таких систем: переход к динамической системе со стохастическим графом обычно приводит к (1) изучению цепей Маркова (с конкретной структурой, управляемой составляющими GDS) и (2) результирующие цепи Маркова имеют тенденцию быть большими и иметь экспоненциальное число состояний. Центральная цель исследования стохастической GDS - создание редуцированных моделей.
Можно также рассмотреть случай, когда вершинные функции являются стохастическими, т.е. функция стохастическая GDS. Например, случайные логические сети являются примерами стохастической GDS функции, использующей схему синхронного обновления и где пространство состояний равно K = {0, 1}. Конечные вероятностные клеточные автоматы (PCA) - еще один пример функции стохастической GDS. В принципе, класс систем взаимодействующих частиц (IPS) охватывает конечные и бесконечные PCA, но на практике работа над IPS в значительной степени связана с бесконечным случаем, поскольку это позволяет вводить более интересные топологии в пространстве состояний.
Графические динамические системы составляют естественную основу для описания распределенных систем, таких как биологические сети и эпидемии, в социальных сетях, многие из которых часто называют сложными системами.