Динамический механический анализ

редактировать

Динамический механический анализ
Другие методы
Акроним	DMA
Классификация	Термический анализ
Связанные	Изотермическая калориметрия титрования. Динамический механический анализ. Термомеханический анализ. Термогравиметрический анализ. Дифференциальный термический анализ. Диэлектрический термический анализ

Динамический механический анализ (сокращенно DMA ) - это метод, используемый для изучения и определения характеристик материалов. Это наиболее полезно для изучения вязкоупругого поведения полимеров. Применяется синусоидальное напряжение и измеряется деформация в материале, что позволяет определить комплексный модуль. температура образца или частота напряжения часто изменяются, что приводит к изменениям комплексного модуля; этот подход можно использовать для определения местоположения температуры стеклования материала, а также для идентификации переходов, соответствующих другим молекулярным движениям.

Содержание

1 Теория
- 1.1 Вязкоупругие свойства материалов
- 1.2 Динамические модули полимеров
  - 1.2.1 Определение динамических модулей
2 Области применения
- 2.1 Измерение температуры стеклования
- 2.2 Полимерный состав
3 Аппаратура
- 3.1 Типы анализаторов
- 3.2 Режимы испытаний
  - 3.2.1 Температурная развертка
  - 3.2.2 Развертка по частоте
  - 3.2.3 Исследования динамического напряжения-деформации
  - 3.2.4 Комбинированная развертка
4 См. Также
5 Ссылки
6 Внешние ссылки

Теория

Вязкоупругие свойства материалов

Рис. 1. Типичный тестер прямого доступа к памяти с захватами для хранения образца и камеры окружающей среды для обеспечения различных температурных режимов. Образец устанавливается на захватах, и камера окружающей среды может сдвигаться, закрывая образец.

Полимеры, состоящие из длинных молекулярных цепочек, обладают уникальными вязкоупругими свойствами, которые сочетают в себе характеристики эластичных твердых тел и Ньютоновские жидкости. Классическая теория упругости описывает механические свойства упругого твердого тела, где напряжение пропорционально деформации при малых деформациях. Такая реакция на напряжение не зависит от скорости деформации. Классическая теория гидродинамики описывает свойства вязкой жидкости, для которой реакция на напряжение зависит от скорости деформации. Такое твердое и жидкое поведение полимеров можно моделировать механически с помощью комбинации пружин и дроссельных заслонок.

Динамические модули полимеров

Вязкоупругие свойства полимера изучаются с помощью динамического механического анализа, в котором синусоидальная сила (напряжение σ) прикладывается к материалу и измеряется результирующее смещение (деформация). Для идеально эластичного твердого тела результирующая деформация и напряжение будут идеально совпадать по фазе. Для чисто вязкой жидкости фазовая задержка деформации по отношению к напряжению будет составлять 90 градусов. Вязкоупругие полимеры обладают промежуточными характеристиками, при которых во время испытаний прямого доступа к памяти возникает некоторое отставание фазы . Когда прилагается деформация и напряжение отстает, выполняются следующие уравнения:

Напряжение: $σ = σ 0 sin ⁡ (t ω + δ) {\ displaystyle \ sigma = \ sigma _ {0} \ sin (T \ omega + \ delta) \,}$ $\ сигма = \ сигма _ {0} \ sin (t \ omega + \ delta) \,$
Напряжение: $ε = ε 0 sin ⁡ (t ω) {\ displaystyle \ varepsilon = \ varepsilon _ {0} \ sin (t \ omega)}$ $\ varepsilon = \ varepsilon _ {0} \ sin (т \ omega)$

где

ω {\ displaystyle \ omega}

\ omega

- частота колебаний деформации,

t {\ displaystyle t}

t

- время,

δ {\ displaystyle \ delta}

\ delta

- фазовая задержка между напряжением и деформацией.

Рассмотрим чисто упругий случай, когда напряжение пропорционально деформации. Имеем. $σ (t) = E ϵ (t) ⟹ σ 0 грех ⁡ (ω t + δ) = E sin 0 sin t ω t = δ = 0 {\ displaystyle \ sigma (t) = E \ epsilon (t) \ подразумевает \ sigma _ {0} \ sin {(\ omega t + \ delta)} = E \ epsilon _ {0} \ sin {\ omega t} \ implies \ delta = 0}$ ${\ displaystyle \ sigma (t) = E \ epsilon (t) \ implies \ sigma _ {0} \ sin {(\ omega t + \ delta)} = E \ epsilon _ {0 } \ sin {\ omega t} \ подразумевает \ delta = 0}$

Теперь для чисто вязкого случая, когда напряжение пропорционально скорости деформации.. $σ (t) = K d ϵ dt ⟹ σ 0 sin ⁡ (ω t + δ) = K ϵ 0 ω cos ⁡ ω t ⟹ δ знак равно π 2 {\ displaystyle \ sigma (t) = K {\ frac {d \ epsilon} {dt}} \ подразумевает \ sigma _ {0} \ sin {(\ omega t + \ delta)} = K \ epsilon _ {0} \ omega \ cos {\ omega t} \ подразумевает \ delta = {\ frac {\ pi} {2}}}$ ${\ displaystyle \ sigma (t) = K {\ frac {d \ epsilon} {dt}} \ подразумевает \ sigma _ {0} \ sin {(\ omega t + \ delta)} = K \ epsilon _ {0} \ omega \ cos {\ omega t} \ подразумевает \ delta = {\ frac {\ pi} {2}}}$

Модуль накопления измеряет накопленную энергию, представляющую упругую часть, и модуль потерь измеряет энергию, рассеиваемую как тепло, представляющую вязкую часть. Модули накопления при растяжении и потерь определяются следующим образом:

Модуль упругости: $E '= σ 0 ε 0 cos ⁡ δ {\ displaystyle E' = {\ frac {\ sigma _ {0}} {\ varepsilon _ {0}}} \ cos \ delta}$ $E'={\frac {\sigma _{0}}{\varepsilon _{0}}}\cos \delta$
Модуль потерь: $E ″ = σ 0 ε 0 sin ⁡ δ {\ displaystyle E '' = {\ frac {\ sigma _ {0}} {\ varepsilon _ {0}}} \ sin \ delta}$ $E''={\frac {\sigma _{0}}{\varepsilon _{0}}}\sin \delta$
Фазовый угол: $δ = arctan ⁡ E ″ E ′ {\ displaystyle \ delta = \ arctan {\ frac {E ''} {E '}} }$ $\delta =\arctan {\frac {E''}{E'}}$

Аналогичным образом мы также определяем накопление при сдвиге и модули потерь, $G ′ {\ displaystyle G '}$ $G'$ и $G ″ {\ displaystyle G' '}$ $G''$ .

Сложные переменные могут использоваться для выражения модулей $E ∗ {\ displaystyle E ^ {*}}$ $E ^ {*}$ и $G ∗ {\ displaystyle G ^ {*}}$ $G ^ *$ следующим образом:

E ∗ = E ′ + i E ″ {\ displaystyle E ^ {*} = E '+ iE' '\,}

E^{*}=E'+iE''\,

G ∗ = G ′ + i G ″ {\ displaystyle G ^ {*} = G '+ iG' '\,}

G^{*}=G'+iG''\,

где

i 2 = - 1 {\ displaystyle {i} ^ {2} = - 1 \,}

{\ displaystyle {i} ^ {2} = - 1 \,}

Вывод динамического модули

Напряжение сдвига $σ (t) = ∫ - ∞ t G (t - t ′) γ ˙ (t ′) dt ′ {\ displaystyle \ sigma (t) = \ int _ {- \ inft y} ^ {t} G (t-t ') {\ dot {\ gamma}} (t') dt '}$ $\sigma (t)=\int _{-\infty }^{t}G(t-t'){\dot {\gamma }}(t')dt'$ конечного элемента в одном направлении можно выразить с помощью модуля релаксации $G (t - t ′) {\ displaystyle G (t-t ')}$ $G(t-t')$ и скорость деформации, интегрированные за все прошлые времена $t ′ {\ displaystyle t'}$ $t'$ до текущего времени $t {\ displaystyle t}$ $t$ . Со скоростью деформации $γ (t) ˙ знак равно ω ⋅ γ 0 ⋅ cos ⁡ (ω t) {\ displaystyle {\ dot {\ gamma (t)}} = \ omega \ cdot \ gamma _ {0} \ cdot \ cos (\ omega t)}$ ${\ displaystyle {\ dot {\ gamma (t)}} = \ omega \ cdot \ gamma _ {0} \ cdot \ cos (\ omega t)}$ и замена $ξ (t ′) = t - t ′ = s {\ displaystyle \ xi (t ') = t-t' = s}$ $\xi (t')=t-t'=s$ получаем $σ (t) = ∫ ξ (- ∞) = t - (- ∞) ξ (t) = t - t G (s) ω γ 0 ⋅ cos ⁡ (ω (t - s)) (- ds) знак равно γ 0 ∫ 0 ∞ ω G (s) соз ⁡ (ω (t - s)) ds {\ displaystyle \ sigma (t) = \ int _ {\ xi (- \ infty) = t - (- \ infty)} ^ {\ xi (t) = tt} G (s) \ omega \ gamma _ {0} \ cdot \ cos (\ omega (ts)) (- ds) = \ gamma _ { 0} \ int _ {0} ^ {\ infty} \ omega G (s) \ cos (\ omega (ts)) ds}$ ${\ displaystyle \ sigma (t) = \ int _ {\ xi (- \ infty) = t - (- \ infty)} ^ {\ xi (t) = tt} G (s) \ omega \ gamma _ {0} \ cdot \ cos (\ omega (ts)) (-ds) = \ гамма _ {0} \ int _ {0} ^ {\ infty} \ omega G (s) \ cos (\ omega (ts)) ds}$ . Применение тригонометрической теоремы сложения $cos ⁡ (x ± y) = cos ⁡ (x) cos ⁡ (y) ∓ sin ⁡ (x) sin ⁡ (y) {\ displaystyle \ cos (x \ pm y) = \ cos (x) \ cos (y) \ mp \ sin (x) \ sin (y)}$ ${\ displaystyle \ соз (x \ pm y) = \ соз (x) \ cos (y) \ mp \ sin (x) \ sin (y)}$ приводят к выражению

σ (t) γ (t) = [ω ∫ o ∞ G (s) sin ⁡ (ω s) ds] ⏟ модуль накопления сдвига G ′ sin ⁡ (ω t) + [ω ∫ o ∞ G (s) cos ⁡ (ω s) ds] ⏟ модуль сдвиговых потерь G ″ cos ⁡ (ω t). {\ displaystyle {\ frac {\ sigma (t)} {\ gamma (t)}} = \ underbrace {[\ omega \ int _ {o} ^ {\ infty} G (s) \ sin (\ omega s) ds]} _ {{\ text {модуль упругости при сдвиге}} G '} \ sin (\ omega t) + \ underbrace {[\ omega \ int _ {o} ^ {\ infty} G (s) \ cos (\ omega s) ds]} _ {{\ text {модуль потерь на сдвиг}} G ''} \ cos (\ omega t). \,}

{\frac {\sigma (t)}{\gamma (t)}}=\underbrace {[\omega \int _{o}^{\infty }G(s)\sin(\omega s)ds]} _{{\text{shear storage modulus }}G'}\sin(\omega t)+\underbrace {[\omega \int _{o}^{\infty }G(s)\cos(\omega s)ds]} _{{\text{shear loss modulus }}G''}\cos(\omega t).\,

со сходящимися интегралами, если $G (s) → 0 { \ displaystyle G (s) \ rightarrow 0}$ ${\ displaystyle G ( s) \ rightarrow 0}$ для $s → ∞ {\ displaystyle s \ rightarrow \ infty}$ ${\ displaystyle s \ rightarrow \ infty}$ , которые зависят от частоты, но не от времени. Расширение $σ (T) знак равно σ 0 ⋅ грех ⁡ (ω ⋅ T + Δ φ) {\ displaystyle \ sigma (t) = \ sigma _ {0} \ cdot \ sin (\ omega \ cdot t + \ Delta \ varphi)}$ ${\ displaystyle \ sigma (t) = \ sigma _ {0} \ cdot \ sin (\ omega \ cdot t + \ Delta \ varphi)}$ с тригонометрическим тождеством $sin ⁡ (x ± y) = sin ⁡ (x) ⋅ cos ⁡ (y) ± cos ⁡ (x) ⋅ sin ⁡ (y) {\ displaystyle \ sin (x \ pm y) = \ sin (x) \ cdot \ cos (y) \ pm \ cos (x) \ cdot \ sin (y)}$ ${\ Displaystyle \ грех (х \ пм у) = \ грех (х) \ CDOT \ соз (у) \ пм \ соз (х) \ CDOT \ грех (у)}$ приводит к

σ (t) γ (t) = σ 0 γ 0 ⋅ cos ⁡ (Δ φ) ⏟ G ′ ⋅ sin ⁡ (ω ⋅ t) + σ 0 γ 0 ⋅ sin ⁡ (Δ φ) ⏟ G ″ ⋅ cos ⁡ (ω ⋅ t) {\ displaystyle {\ frac {\ sigma (t)} {\ gamma (t)}} = \ underbrace {{\ frac {\ sigma _ {0}} {\ gamma _ {0}}} \ cdot \ cos (\ Delta \ varphi)} _ {G '} \ cdot \ sin (\ omega \ cdot t) + \ underbrace {{\ frac {\ sigma _ {0}} {\ gamma _ {0}}} \ cdot \ грех (\ Delta \ varphi)} _ {G ''} \ cdot \ cos (\ omega \ cdot t) \,}

{\frac {\sigma (t)}{\gamma (t)}}=\underbrace {{\frac {\sigma _{0}}{\gamma _{0}}}\cdot \cos(\Delta \varphi)} _{G'}\cdot \sin(\omega \cdot t)+\underbrace {{\frac {\sigma _{0}}{\gamma _{0}}}\cdot \sin(\Delta \varphi)} _{G''}\cdot \cos(\omega \cdot t)\,

Сравнение двух $σ (t) γ (t) {\ displaystyle { \ frac {\ sigma (t)} {\ gamma (t)}}}$ ${\ displaystyle {\ frac {\ sigma (t)} {\ gamma (t)}}}$ уравнения приводят к определению $G ′ {\ displaystyle G '}$ $G'$ и $G ″ {\ displaystyle G ''}$ $G''$ .

Приложения

Измерение стеклования te Температура

Одним из важных приложений прямого доступа к памяти является измерение температуры стеклования полимеров. Аморфные полимеры имеют разные температуры стеклования, выше которых материал будет иметь каучукоподобные свойства вместо стекловидного поведения, и жесткость материала будет резко падать вместе со снижением его вязкости. При стекловании модуль накопления резко уменьшается, а модуль потерь достигает максимума. DMA с динамической температурой часто используется для характеристики температуры стеклования материала.

Рис. 2. Типичная термограмма DMA аморфного термопласта (поликарбоната). Модуль упругости (E ’), модуль потерь (E’ ’) и коэффициент потерь tan (дельта) нанесены на график как функция температуры. Было обнаружено, что температура стеклования поликарбоната составляет около 151 ° C (оценка в соответствии с ISO 6721-11)

Полимерный состав

Изменение состава мономеров и сшивание может добавить или изменить функциональность полимера, что может изменить результаты, полученные от DMA. Пример таких изменений можно увидеть при смешивании этилен-пропилендиенового мономера (EPDM) с стирол-бутадиеновым каучуком (SBR) и различными системами сшивания или отверждения. Наир и др. сокращенно смеси обозначают E 0 S, E 20 S и т. д., где E 0 S равно массовому проценту EPDM в смеси, а S обозначает серу как отвердитель.

Увеличение количества SBR в смеси снижает модуль упругости из-за межмолекулярного и внутримолекулярного взаимодействий, которые могут изменять физическое состояние полимера. В стеклообразной области EPDM показывает самый высокий модуль упругости из-за более сильных межмолекулярных взаимодействий (SBR имеет более стерические препятствия, что делает его менее кристаллическим). В каучуковой области SBR показывает самый высокий модуль упругости, обусловленный его способностью противостоять межмолекулярному проскальзыванию.

По сравнению с серой, более высокий модуль упругости наблюдается для смесей, отвержденных дикумилпероксидом (DCP) из-за относительной прочности облигаций СС и НЦБ.

Включение усиливающих наполнителей в полимерные смеси также увеличивает модуль накопления за счет ограничения высоты пика тангенса угла потерь.

ДМА также можно использовать для эффективной оценки смешиваемости полимеров. Смесь E 40 S имела гораздо более широкий переход с уступом вместо крутого спада на графике накопительного модуля при различных соотношениях смеси, что указывает на то, что есть области, которые не являются однородными.

Инструментарий

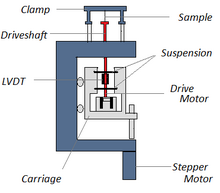Рисунок 3. Общая схема инструмента прямого доступа к памяти.

Инструментарий прямого доступа к памяти состоит из датчика смещения, такого как линейный переменный дифференциальный трансформатор, который измеряет изменение напряжения как результат движения измерительного зонда через магнитный сердечник, систему контроля температуры или печь, приводной двигатель (линейный двигатель для нагружения зонда, который обеспечивает нагрузку для приложенной силы), опору приводного вала и систему направления, которые действуют как направляющие для силы, прилагаемой двигателем к образцу, и зажимы для образцов, чтобы удерживать испытуемый образец. В зависимости от того, что измеряется, образцы будут готовиться и обрабатываться по-разному. Общая схема основных компонентов инструмента прямого доступа к памяти показана на рисунке 3.

Типы анализаторов

В настоящее время используются два основных типа анализаторов прямого доступа к памяти: анализаторы принудительного резонанса и анализаторы свободного резонанса.. Анализаторы свободного резонанса измеряют свободные колебания демпфирования испытуемого образца путем подвешивания и качания образца. Ограничение для анализаторов свободного резонанса состоит в том, что они ограничиваются образцами стержневой или прямоугольной формы, но также применимы образцы, которые можно плести / плести. Анализаторы принудительного резонанса - наиболее распространенный тип анализаторов, доступных сегодня в приборостроении. Эти типы анализаторов заставляют образец колебаться с определенной частотой и надежны для выполнения температурной развертки.

Рисунок 4. Крутильные и осевые движения.

Анализаторы предназначены как для контроля напряжения (силы), так и деформации (смещения). При контроле деформации зонд смещается, и результирующее напряжение образца измеряется с помощью датчика баланса сил, который использует разные валы. К преимуществам контроля деформации относится более короткое время отклика для материалов с низкой вязкостью, а эксперименты по снятию напряжения проводятся с относительной легкостью. При контроле напряжения к образцу прикладывается заданная сила, и можно изменять несколько других экспериментальных условий (температура, частота или время). Контроль напряжения обычно дешевле, чем контроль деформации, потому что нужен только один вал, но это также затрудняет его использование. Некоторые преимущества контроля напряжения включают тот факт, что структура образца с меньшей вероятностью будет разрушена, и более длительное время релаксации / более длительные исследования ползучести могут быть выполнены с гораздо большей легкостью. Недостатком характеристики материалов с низкой вязкостью является короткое время отклика, ограниченное инерцией. Анализаторы контроля напряжения и деформации дают примерно одинаковые результаты, если характеристика находится в пределах линейной области рассматриваемого полимера. Однако контроль напряжения дает более реалистичный отклик, потому что полимеры имеют тенденцию противостоять нагрузке.

Напряжение и деформация можно прикладывать с помощью крутильных или осевых анализаторов. Анализаторы крутильных колебаний в основном используются для жидкостей или расплавов, но также могут применяться для некоторых твердых образцов, поскольку сила прикладывается в виде вращательного движения. Инструмент может проводить эксперименты по восстановлению ползучести, релаксации напряжений и напряжений-деформаций. Осевые анализаторы используются для твердых или полутвердых материалов. Он может проводить испытания на изгиб, растяжение и сжатие (при желании даже образцы на сдвиг и жидкие образцы). Эти анализаторы могут тестировать материалы с более высоким модулем упругости, чем анализаторы крутильных колебаний. Прибор может выполнять термомеханический анализ (ТМА) в дополнение к экспериментам, которые могут выполнять анализаторы крутильных колебаний. На рисунке 4 показано общее различие между двумя приложениями напряжения и деформации.

Изменение геометрии образца и креплений может сделать анализаторы напряжения и деформации практически безразличными друг к другу, за исключением крайних концов фаз образца, т.е. жесткие материалы. Общие геометрические формы и приспособления для аксиальных анализаторов включают трехточечный и четырехточечный изгиб, двойную и одинарную консоль, параллельную пластину и варианты, объемные, растягивающие / растягивающие и сдвиговые пластины и многослойные конструкции. Геометрия и приспособления для анализаторов крутильных колебаний состоят из параллельных пластин, конуса и пластины, куэта, а также торсионной балки и оплетки. Чтобы использовать прямой доступ к памяти для характеристики материалов, необходимо обратить внимание на тот факт, что небольшие размерные изменения могут также привести к большим неточностям в определенных тестах. Инерционный и сдвиговый нагрев могут повлиять на результаты работы анализаторов принудительного или свободного резонанса, особенно в пробах жидкости.

Режимы испытаний

Для исследования вязкоупругих свойств жидкости можно использовать два основных режима испытаний. полимеры: тесты на изменение температуры и частоты. Третий, менее изучаемый режим испытаний - это динамическое испытание на нагрузку и деформацию.

Температурная развертка

Обычный метод испытаний включает измерение комплексного модуля упругости на низкой постоянной частоте при изменении температуры образца. Выраженный пик в $tan ⁡ (δ) {\ displaystyle \ tan (\ delta)}$ ${\ displaystyle \ tan (\ delta)}$ появляется при температуре стеклования полимера. Также могут наблюдаться вторичные переходы, которые можно объяснить зависимой от температуры активацией широкого спектра цепных движений. В полукристаллических полимерах можно наблюдать отдельные переходы для кристаллических и аморфных участков. Точно так же множественные переходы часто встречаются в смесях полимеров.

Например, смеси поликарбоната и поли (акрилонитрил-бутадиен-стирол ) были изучены с целью разработки материала на основе поликарбоната без тенденции поликарбоната к хрупкое разрушение. DMA смесей с динамической температурной разверткой показал два сильных перехода, совпадающих с температурами стеклования ПК и PABS, что согласуется с выводом о том, что два полимера не смешивались.

Развертка по частоте

Рисунок 5. Развертка по частоте испытание на поликарбонате при комнатной температуре (25 ° C). Модуль упругости (E ’) и модуль потерь (E’ ’) наносили на график в зависимости от частоты. Увеличение частоты «замораживает» движения цепи, и наблюдается более жесткое поведение.

Образец можно выдерживать при фиксированной температуре и тестировать с различной частотой. Пики в $tan ⁡ (δ) {\ displaystyle \ tan (\ delta)}$ ${\ displaystyle \ tan (\ delta)}$ и в E '' относительно частоты могут быть связаны со стеклованием, что соответствует способности цепей проходить друг мимо друга. Обратите внимание, что это означает, что стеклование зависит не только от температуры, но и от скорости деформации. Также могут наблюдаться вторичные переходы.

Модель Максвелла обеспечивает удобное, если не строго точное, описание вязкоупругих материалов. Применение синусоидального напряжения к модели Максвелла дает: $E ″ = E τ 0 ω τ 0 2 ω 2 + 1, {\ displaystyle E '' = {\ frac {E \ tau _ {0} \ omega} { \ tau _ {0} ^ {2} \ omega ^ {2} +1}},}$ $E''={\frac {E\tau _{0}\omega }{\tau _{0}^{2}\omega ^{2}+1}},$ где $τ 0 = η / E {\ displaystyle \ tau _ {0} = \ eta / E}$ ${\ displaystyle \ tau _ {0} = \ eta / E}$ - время релаксации Максвелла. Таким образом, пик E ’’ наблюдается на частоте $1 / τ 0 {\ displaystyle 1 / \ tau _ {0}}$ ${\ displaystyle 1 / \ tau _ { 0}}$ . Реальный полимер может иметь несколько разных времен релаксации, связанных с разными молекулярными движениями.

Исследование динамического напряжения-деформации

Постепенно увеличивая амплитуду колебаний, можно выполнять динамическое измерение напряжения-деформации. Изменение модулей накопления и потерь с увеличением напряжения можно использовать для характеристики материалов и для определения верхней границы линейного режима напряжения-деформации материала.

Комбинированная развертка

Поскольку стеклование и вторичные переходы наблюдаются как в частотных исследованиях, так и в исследованиях температуры, есть интерес к многомерным исследованиям, когда температурные колебания проводятся на различных частотах или частотные колебания проводятся при различных температурах. Такого рода исследования дают богатую характеристику материала и могут предоставить информацию о природе молекулярного движения, ответственного за переход.

Например, исследования полистирола (Tg≈110 ° C) отметили вторичный переход около комнатной температуры. Температурно-частотные исследования показали, что температура перехода в значительной степени не зависит от частоты, предполагая, что этот переход является результатом движения небольшого числа атомов; было высказано предположение, что это результат вращения фенильной группы вокруг основной цепи.

См. также

Ссылки

Внешние ссылки

KBDF в FCC База данных FM-станций
KBDF на Radio-Locator
KBDF в Nielsen Audio База данных FM-станций

Dynamical Mechanical Analysis Получено 21 мая 2019 г.