 A многопоточное дерево со специальными связями потоков, показанными пунктирными стрелками
A многопоточное дерево со специальными связями потоков, показанными пунктирными стрелками В вычислениях, многопоточное двоичное дерево - это вариант двоичного дерева, который упрощает обход в определенном порядке (часто в том же порядке, который уже определен для дерева).
Все двоичное дерево сортировки можно легко обойти в порядке основного ключа, но при наличии только указателя на узел поиск следующего узла может быть медленным или невозможным. Например, листовые узлы по определению не имеют потомков, поэтому ни один другой узел не может быть достигнут при наличии только указателя на листовой узел - конечно, который включает желаемый «следующий» узел. Многопоточное дерево добавляет дополнительную информацию в некоторые или все узлы, поэтому «следующий» узел может быть найден быстро. Его также можно пройти без рекурсии и без дополнительной памяти (пропорциональной глубине дерева), которая требуется.
Определено многопоточное двоичное дерево следующим образом:
«Бинарное дерево распределяется по потокам, делая все правые дочерние указатели, которые обычно были бы нулевыми точками для упорядоченного преемника узла (, если он существует), и все левые дочерние указатели это обычно будет нулевой точкой для упорядоченного предшественника узла. "
Это определение предполагает, что порядок обхода такой же, как и обход дерева по порядку. Однако указатели могут вместо этого (или в дополнение) быть добавлены к узлам дерева, вместо того, чтобы заменять связанные списки., определенные таким образом, также обычно называются "потоками" и могут использоваться для включения обхода в любом порядке (ах). желанный. Например, дерево, узлы которого представляют информацию о людях, может быть отсортировано по имени, но иметь дополнительные потоки, позволяющие быстро перемещаться по дате рождения, весу или любой другой известной характеристике.
Деревья, включая (но не ограничиваясь) деревья двоичного поиска, могут использоваться для хранения элементов в определенном порядке, например значения некоторого свойства хранится в каждом узле, часто называется ключом . Одна из полезных операций в таком дереве - обход: просмотр всех элементов в порядке ключа.
Ниже приводится алгоритм простого рекурсивного обхода, который посещает каждый узел двоичного дерева поиска. Предположим, что t - указатель на узел, или ноль. «Посещение» t может означать выполнение любого действия с узлом t или его содержимым.
Перемещение алгоритма (t):
Одна проблема с этим алгоритмом состоит в том, что из-за его рекурсии он использует пространство стека, пропорциональное высоте дерева. Если дерево достаточно сбалансировано, это составляет O (log n) пространства для дерева, содержащего n элементов. В худшем случае, когда дерево принимает форму цепочки , высота дерева равна n, поэтому алгоритм занимает O (n) пространства. Вторая проблема заключается в том, что все обходы должны начинаться с корня, если узлы имеют указатели только на своих дочерних узлов. Обычно имеется указатель на конкретный узел, но этого недостаточно для возврата к остальной части дерева, если не добавлена дополнительная информация, например указатели потоков.
В этом подходе может быть невозможно определить, действительно ли левый и / или правый указатели в данном узле указывают на дочерние элементы или являются следствием многопоточности. Если различение необходимо, для его записи достаточно добавить по одному биту к каждому узлу.
В учебнике 1968 года Дональд Кнут спросил, существует ли нерекурсивный алгоритм обхода по порядку, который не использует стек и оставляет дерево неизмененным. Одно из решений этой проблемы - распараллеливание дерева, представленное Дж. Х. Моррис в 1979 году. В последующем издании 1969 года Кнут приписал представление дерева с нитями Перлису и Торнтону (1960).
Другой способ достичь аналогичных целей - включить в каждый узел указатель на родительский узел этого узла. При этом «следующий» узел всегда доступен. "правильные" указатели по-прежнему равны нулю, если нет правильных потомков. Чтобы найти «следующий» узел от узла, правый указатель которого равен нулю, пройдите через «родительские» указатели до тех пор, пока не дойдете до узла, правый указатель которого не равен нулю и не является потомком, из которого вы только что вышли. Этот узел является «следующим» узлом, а после него идут его потомки справа.
Также возможно обнаружить родительский узел из многопоточного двоичного дерева, без явного использования родительских указателей или стека, хотя это медленнее. Чтобы убедиться в этом, рассмотрим узел k с правым дочерним элементом r. Тогда левый указатель r должен быть либо потомком, либо потоком, возвращающимся к k. В случае, если у r есть левый дочерний элемент, этот левый дочерний элемент должен, в свою очередь, иметь либо собственный левый дочерний элемент, либо поток, возвращающийся к k, и так далее для всех последующих левых дочерних элементов. Таким образом, следуя цепочке левых указателей от r, мы в конечном итоге найдем поток, указывающий обратно на k. Ситуация симметрично аналогична, когда q является левым потомком p - мы можем проследить за правыми потомками q до нити, указывающей вперед на p.
В Python :
def parent (node): если node - это node.tree.root: return None else: x = node y = node while True: if is_thread (y): p = y.right если p равно None или p.left не является узлом: p = x, а не is_thread (p.left): p = p.left p = p.left return p elif is_thread (x): p = x.left, если p равно None или p.right не является узлом: p = y, а не is_thread (p.right): p = p.right p = p.right return px = x.left y = y.right
Потоки - это ссылки на предшественников и последователей узла в соответствии с обходом без порядка.
В порядке обход дерева потоков: A, B, C, D, E, F, G, H, I, предшественником Eявляется D, преемником Eявляется F.


Давайте сделаем многопоточное двоичное дерево из обычного двоичного дерева:
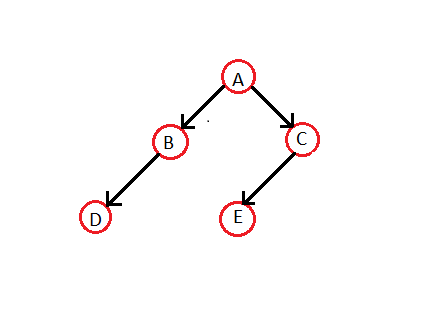
в порядке обход для приведенного выше дерева - DBAE C. Таким образом, соответствующее многопоточное двоичное дерево будет -

В многопоточном двоичном дереве с n узлами имеется n * m - (n-1) недействительные ссылки.
Поскольку это нерекурсивный метод обхода, он должен быть итеративной процедурой; Это означает, что все шаги для обхода узла должны выполняться в цикле, чтобы то же самое можно было применить ко всем узлам в дереве.
Мы снова рассмотрим обход IN-ORDER. Здесь для каждого узла мы сначала посетим левое поддерево (если оно существует) (если и только если мы не посещали его ранее); затем мы посещаем (т.е. печатаем его значение, в нашем случае) сам узел, а затем правое поддерево (если оно существует). Если правого поддерева нет, мы проверяем наличие многопоточной ссылки и делаем узел с резьбой текущим рассматриваемым узлом. Пожалуйста, следуйте примеру, приведенному ниже.

| Li | ||||
|---|---|---|---|---|
| шаг-1 | 'A' имеет левый дочерний элемент, то есть B, который не был посещен. Итак, мы помещаем B в наш «список посещенных узлов», и B становится нашим текущим узлом. | B | ||
| step-2 | 'B' также имеет левый дочерний элемент 'D', который не является есть в нашем списке посещенных узлов. Итак, мы помещаем «D» в этот список и рассматриваем его как текущий узел. | BD | ||
| step-3 | «D» не имеет левого дочернего элемента, поэтому мы печатаем « D '. Затем мы проверяем его правого ребенка. «D» не имеет правого потомка, поэтому мы проверяем его ссылку на поток. У него есть поток, идущий до узла «B». Итак, мы рассматриваем в качестве текущего узла 'B'. | BD | D | |
| step-4 | 'B' определенно имеет левый дочерний элемент, но он уже в нашем списке посещенных узлов. Итак, печатаем "B". Затем мы проверяем его правого дочернего элемента, но его не существует. Итак, мы рассматриваем его многопоточный узел (то есть 'A') в качестве текущего. | BD | DB | |
| step-5 | 'A' имеет левый дочерний элемент «B», но он уже присутствует в списке посещенных узлов. Итак, печатаем «А». Затем мы проверяем его правого ребенка. «A» имеет правильный дочерний элемент «C», и его нет в нашем списке посещенных узлов. Итак, мы добавляем его в этот список и рассматриваем как текущий узел. | BDC | DBA | |
| step-6 | 'C' имеет 'E 'как левый дочерний элемент, и его даже нет в нашем списке посещенных узлов. Итак, мы добавляем его в этот список и делаем его нашим текущим узлом. | BDCE | DBA | |
| step-7 | и, наконец,..... | DBAEC |