Алгоритм спиральной оптимизации

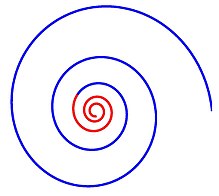
Спираль разделяет глобальное (синий) и интенсивный (красный) поведение

спиральная оптимизация (SPO) Алгоритм - это несложная концепция поиска, вдохновленная спиральными явлениями в природе. Первый алгоритм SPO был предложен для двумерной безусловной оптимизации на основе двумерных спиральных моделей. Это было распространено на n-мерные проблемы путем обобщения двумерной спиральной модели на n-мерную спиральную модель. Существуют эффективные настройки для алгоритма SPO: настройка направления периодического спуска и настройка сходимости.

• 1 Метафора
• 2 Алгоритм
• 3 Настройка
  • 3.1 Настройка 1 (Настройка направления периодического спуска)
  • 3.2 Настройка 2 (Настройка конвергенции)
• 4 Будущие работы
• 5 Расширенные работы
• 6 Ссылки

Мотивация для сосредоточения внимания на спиральных явлениях было связано с пониманием того, что динамика, порождающая логарифмические спирали, разделяет поведение диверсификации и интенсификации. Поведение диверсификации может работать для глобального поиска (исследования), а поведение интенсификации позволяет интенсивный поиск текущего найденного хорошего решения (эксплуатация).

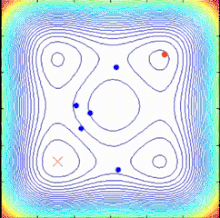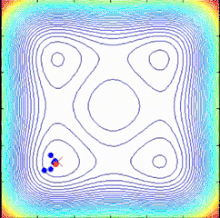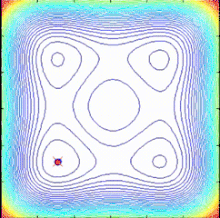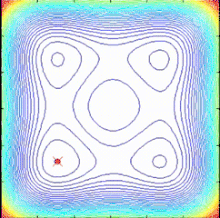
Алгоритм спиральной оптимизации (SPO)

Алгоритм SPO - это алгоритм многоточечного поиска, не имеющий градиента целевой функции, который использует несколько спиральных моделей, которые могут быть описаны как детерминированные динамические системы. Поскольку точки поиска следуют по логарифмическим спиральным траекториям к общему центру, определяемому как текущая лучшая точка, могут быть найдены лучшие решения и общий центр может быть обновлен. Общий алгоритм SPO для задачи минимизации при максимальной итерации $k\; max\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; max\}\}$(критерий завершения) выглядит следующим образом:

0) Установите количество точек поиска $m\; \ge \; 2\; \{\backslash \; displaystyle\; m\; \backslash \; geq\; 2\}$и максимальное количество итераций $k\; max\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; max\}\}$. 1) Поместите начальные точки поиска $xi\; (0)\; \in \; R\; n\; (i\; =\; 1,\dots ,\; m)\; \{\backslash \; displaystyle\; x\_\; \{i\}\; (0)\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\; ~\; (i\; =\; 1,\; \backslash \; ldots,\; m)\}$и определите центр $x\; \star \; (0)\; =\; xib\; (0)\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; star\}\; (0)\; =\; x\_\; \{i\; \_\; \{\backslash \; текст\; \{b\}\}\}\; (0)\}$, $ib\; =\; argmin\; i\; =\; 1,\dots ,\; m\; \; \{f\; (xi\; (0))\}\; \{\backslash \; displaystyle\; \backslash \; displaystyle\; i\; \_\; \{\backslash \; text\; \{b\}\}\; =\; \backslash \; mathop\; \{\; \backslash \; text\; \{argmin\}\}\; \_\; \{i\; =\; 1,\; \backslash \; ldots,\; m\}\; \backslash \; \{f\; (x\_\; \{i\}\; (0))\; \backslash \}\}$, а затем установите $k\; =\; 0\; \{\backslash \; стиль\; отображения\; k\; =\; 0\}$. 2) Определите скорость шага $r\; (k)\; \{\backslash \; displaystyle\; r\; (k)\}$с помощью правила. 3) Обновите точки поиска: $xi\; (k\; +\; 1)\; =\; x\; \star \; (k)\; +\; r\; (k)\; R\; (\theta )\; (xi\; (k)\; -\; x\; \star \; (k))\; (i\; =\; 1,\dots ,\; м).\; \{\backslash \; Displaystyle\; х\_\; \{я\}\; (к\; +\; 1)\; =\; х\; ^\; \{\backslash \; звезда\}\; (к)\; +\; г\; (к)\; р\; (\backslash \; тета)\; (х\_\; \{я\}\; (к)\; -x\; ^\; \{\backslash \; звезда\}\; (к))\; \backslash \; quad\; (i\; =\; 1,\; \backslash \; ldots,\; m).\}$4) Обновить центр: где $ib\; =\; argmin\; i\; =\; 1,\dots ,\; m\; \; \{f\; (xi\; (k\; +\; 1))\}\; \{\backslash \; displaystyle\; \backslash \; displaystyle\; i\; \_\; \{\backslash \; text\; \{b\}\}\; =\; \backslash \; mathop\; \{\backslash \; text\; \{argmin\}\}\; \_\; \{i\; =\; 1,\; \backslash \; ldots,\; m\}\; \backslash \; \{f\; (x\_\; \{i\}\; (k\; +\; 1))\; \backslash \}\}$. 5) Установить $k\; :\; знак\; равно\; к\; +\; 1\; \{\backslash \; Displaystyle\; к:\; =\; к\; +\; 1\}$. Если $k\; =\; k\; max\; \{\backslash \; displaystyle\; k\; =\; k\; \_\; \{\backslash \; max\}\}$выполнено, завершите работу и выведите $x\; \star \; (k)\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; star\}\; (k)\}$. В противном случае вернитесь к шагу 2).

Эффективность поиска зависит от настройки составной матрицы вращения $R\; (\theta )\; \{\backslash \; displaystyle\; R\; (\backslash \; theta)\}$, скорости шага $r\; (k)\; \{\backslash \; displaystyle\; r\; (k)\}$, и начальные точки $xi\; (0)\; (i\; =\; 1,\dots ,\; m)\; \{\backslash \; displaystyle\; x\_\; \{i\}\; (0)\; ~\; (i\; =\; 1,\; \backslash \; ldots,\; m)\}$. Следующие настройки являются новыми и эффективными.

Настройка 1 (настройка направления периодического спуска)

Эта настройка является эффективной настройкой для задач большого размера при максимальной итерации $k\; max\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; max\}\}$. Условия для $R\; (\theta )\; \{\backslash \; displaystyle\; R\; (\backslash \; theta)\}$и $xi\; (0)\; (i\; =\; 1,\dots ,\; m)\; \{\backslash \; displaystyle\; x\_\; \{i\}\; (\; 0)\; ~\; (i\; =\; 1,\; \backslash \; ldots,\; m)\}$вместе гарантируют, что спиральные модели периодически генерируют направления спуска. Условие $r\; (k)\; \{\backslash \; displaystyle\; r\; (k)\}$работает для использования периодических направлений спуска при завершении поиска $k\; max\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; max\}\}$.

• Установите $R\; (\theta )\; \{\backslash \; displaystyle\; R\; (\backslash \; theta)\}$следующим образом: $R\; (\theta )\; =\; [0\; n\; -\; 1\; \top \; -\; 1\; I\; n\; -\; 1\; 0\; n\; -\; 1]\; \{\backslash \; Displaystyle\; R\; (\backslash \; theta)\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\_\; \{n-1\}\; ^\; \{\backslash \; top\}\; -\; 1\; \backslash \backslash \; I\_\; \{n-1\}\; 0\_\; \{n-1\}\; \backslash \backslash \backslash \; конец\; \{bmatrix\}\}\}$где $I\; n\; -\; 1\; \{\backslash \; displaystyle\; I\_\; \{n-1\}\}$- это $(n\; -\; 1)\; \times \; (n\; -\; 1)\; \{\backslash \; displaystyle\; (n-1)\; \backslash \; times\; (n-1)\}$единичная матрица и $0\; n\; -\; 1\; \{\backslash \; displaystyle\; 0\_\; \{n-1\}\}$- $(n\; -\; 1)\; \times \; 1\; \{\backslash \; displaystyle\; (n-1)\; \backslash \; times\; 1\}$нулевой вектор.
• Поместите начальные точки $xi\; (0)\; \in \; Р\; n\; \{\backslash \; displaystyle\; x\_\; \{i\}\; (0)\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\}$$(i\; =\; 1,\dots ,\; m)\; \{\backslash \; displaystyle\; (i\; =\; 1,\; \backslash \; ldots,\; m)\}$произвольно, чтобы удовлетворить следующему условию:

$min\; i\; =\; 1,\dots ,\; m\; \{max\; j\; =\; 1,\dots ,\; m\; \{rank\; [dj,\; i\; (0)\; R\; (\theta )\; dj,\; i\; (0)\; \cdots \; R\; (\theta )\; 2\; n\; -\; 1\; dj,\; i\; (0)]\}\}\; =\; n\; \{\backslash \; disp\; Laystyle\; \backslash \; min\; \_\; \{я\; =\; 1,\; \backslash \; ldots,\; m\}\; \backslash \; \{\backslash \; max\; \_\; \{j\; =\; 1,\; \backslash \; ldots,\; m\}\; \{\backslash \; bigl\; \backslash \; \{\}\; \{\backslash \; text\; \{rank\}\}\; \{\backslash \; bigl\; [\}\; d\_\; \{j,\; i\}\; (0)\; ~\; R\; (\backslash \; theta)\; d\_\; \{j,\; i\}\; (0)\; ~~\; \backslash \; cdots\; ~~\; R\; (\backslash \; theta)\; ^\; \{2n-1\}\; d\_\; \{j,\; i\}\; (0)\; \{\backslash \; bigr\; ]\}\; \{\backslash \; bigr\; \backslash \}\}\; \{\backslash \; bigr\; \backslash \}\}\; =\; n\}$где $dj,\; i\; (0)\; =\; xj\; (0)\; -\; xi\; (0)\; \{\backslash \; displaystyle\; d\_\; \{j,\; i\}\; (0)\; =\; x\_\; \{j\}\; (0)\; -x\_\; \{i\}\; (0)\}$. Обратите внимание, что это условие почти полностью удовлетворяется случайным размещением, и поэтому никакая проверка на самом деле не подходит.

• Задайте $r\; (k)\; \{\backslash \; displaystyle\; r\; (k)\}$на этапе 2) следующим образом: $r\; (k)\; =\; r\; =\; \delta \; k\; max\; (постоянное\; значение)\; \{\; \backslash \; displaystyle\; r\; (k)\; =\; r\; =\; \{\backslash \; sqrt\; [\{k\; \_\; \{\backslash \; max\}\}]\; \{\backslash \; delta\}\}\; ~~~~\; \{\backslash \; text\; \{(постоянное\; значение)\}\}\}$где достаточно small $\delta >0\; \{\backslash \; displaystyle\; \backslash \; delta>0\}$, например $\delta \; =\; 1\; /\; k\; max\; \{\backslash \; displaystyle\; \backslash \; delta\; =\; 1\; /\; k\; \_\; \{\backslash \; max\}\}$или $\delta \; =\; 10\; -\; 3\; \{\backslash \; displaystyle\; \backslash \; delta\; =\; 10\; ^\; \{-\; 3\}\}$.

Настройка 2 (настройка сходимости)

Эта настройка гарантирует, что алгоритм SPO сходится к стационарной точке при максимальной итерации $k\; max\; =\; \infty \; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; max\}\; =\; \backslash \; infty\}$. Параметры $R\; (\theta )\; \{\backslash \; displaystyle\; R\; (\backslash \; theta)\}$и начальные точки $xi\; (0)\; (i\; =\; 1,\dots ,\; m)\; \{\backslash \; displaystyle\; x\_\; \{i\}\; (0)\; ~\; (i\; =\; 1,\; \backslash \; ldots,\; m)\}$совпадают с указанная выше настройка 1. Настройка $r\; (k)\; \{\backslash \; displaystyle\; r\; (\; k)\}$выглядит следующим образом.

• Задайте $r\; (k)\; \{\backslash \; displaystyle\; r\; (k)\}$на шаге 2) следующим образом: $r\; (k)\; =\; \{1\; (k\; \star \; \leqq \; k\; \leqq \; k\; \star \; +\; 2\; N\; -\; 1)\; час\; (К\; \geqq \; К\; \star \; +\; 2\; N),\; \{\backslash \; Displaystyle\; г\; (к)\; =\; \{\backslash \; begin\; \{case\}\; 1\; (k\; ^\; \{\backslash \; star\}\; \backslash \; leqq\; k\; \backslash \; leqq\; k\; ^\; \{\backslash \; star\; \}\; +\; 2n-1),\; \backslash \backslash \; h\; (k\; \backslash \; geqq\; k\; ^\; \{\backslash \; star\}\; +\; 2n),\; \backslash \; end\; \{cases\}\}\}$где $k\; \star \; \{\backslash \; displaystyle\; k\; ^\; \{\backslash \; star\}\}$- это итерация, когда центр обновляется заново на шаге 4) и $h\; =\; \delta \; 2\; n,\; \delta \; \in \; (0,\; 1)\; \{\backslash \; displaystyle\; h\; =\; \{\backslash \; sqrt\; [\{2n\; \}]\; \{\backslash \; delta\}\},\; \backslash \; delta\; \backslash \; in\; (0,1)\}$, например, $\delta \; =\; 0,5\; \{\backslash \; displaystyle\; \backslash \; delta\; =\; 0,5\}$. Таким образом, мы должны добавить в алгоритм следующие правила о $k\; \star \; \{\backslash \; displaystyle\; k\; ^\; \{\backslash \; star\}\}$:

• (Шаг 1) $k\; \star \; =\; 0\; \{\; \backslash \; displaystyle\; k\; ^\; \{\backslash \; star\}\; =\; 0\}$.

• (Шаг 4) Если $x\; \star \; (k\; +\; 1)\; \ne \; x\; \star \; (k)\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; star\}\; (k\; +\; 1)\; \backslash \; neq\; x\; ^\; \{\backslash \; star\}\; (k)\}$, затем $k\; \star \; =\; k\; +\; 1\; \{\backslash \; displaystyle\; k\; ^\; \{\backslash \; star\}\; =\; k\; +\; 1\}$.

• Алгоритмы с указанными выше настройками детерминированы. Таким образом, включение некоторых случайных операций делает этот алгоритм мощным для глобальной оптимизации. Cruz-Duarte et al. продемонстрировал это, включив в спиральные поисковые траектории стохастические возмущения. Однако эта дверь остается открытой для дальнейших исследований.
• Чтобы найти подходящий баланс между спиралями диверсификации и интенсификации в зависимости от целевого класса задачи (включая $k\; max\; \{\backslash \; displaystyle\; k\; \_\; \{\backslash \; max\}\}$) важен для повышения производительности.

Много расширенных исследований было проведено на SPO из-за его простой структуры и концепции; эти исследования помогли повысить эффективность глобального поиска и предложили новые приложения.