Тета-функции Невилла

редактировать

В математике тета-функции Невилла, названные в честь Эрика Гарольда Невилла, определены следующим образом:

θ c (z, m) = 2 π q (m) 1/4 m 1/4 K (m) ∑ k = 0 ∞ (q (m)) k (k + 1) соз ⁡ ((2 К + 1) π Z 2 К (м)) {\ displaystyle \ theta _ {c} (z, m) = {\ frac {{\ sqrt {2 \ pi}} \, q (m) ^ {1/4}} {m ^ {1/4} {\ sqrt {K (m)}}}} \, \, \ sum _ {k = 0} ^ {\ infty} (q (m)) ^ {k (k + 1)} \ cos \ left ({\ frac {(2k + 1) \ pi z} {2K (m)}} \ right)}

{\ displaystyle \ theta _ {c} (z, m) = {\ frac {{\ sqrt {2 \ pi}} \, q (m) ^ {1/4}} {m ^ {1/4} {\ sqrt { K (m)}}}} \, \, \ sum _ {k = 0} ^ {\ infty} (q (m)) ^ {k (k + 1)} \ cos \ left ({\ frac {( 2k + 1) \ pi z} {2K (m)}} \ right)}

θ d (z, m) = 2 π 2 К (м) (1 + 2 ∑ К знак равно 1 ∞ (q (м)) К 2 соз ⁡ (π zk К (м))) {\ Displaystyle \ theta _ {d} (г, м) = {\ frac {\ sqrt {2 \ pi}} {2 {\ sqrt {K (m)}}}} \, \, \ left (1 + 2 \, \ sum _ {k = 1} ^ {\ infty } (q (m)) ^ {k ^ {2}} \ cos \ left ({\ frac {\ pi zk} {K (m)}} \ right) \ right)}

{\ displaystyle \ theta _ {d} (z, m) = {\ frac {\ sqrt {2 \ pi}} {2 {\ sqrt {K (m)}}} } \, \, \ left (1 + 2 \, \ sum _ {k = 1} ^ {\ infty} (q (m)) ^ {k ^ { 2}} \ cos \ left ({\ frac {\ pi zk} {K (m)}} \ right) \ right)}

θ n (z, m) = 2 π 2 (1 - m) 1/4 K (m) (1 + 2 ∑ k = 1 ∞ (- 1) k (q (m)) k 2 cos ⁡ (π zk K (m))) {\ displaystyle \ theta _ {n} (z, m) = {\ frac {\ sqrt {2 \ pi}} {2 (1-m) ^ {1/4} {\ sqrt {K (m)} }}} \, \, \ left (1 + 2 \ sum _ {k = 1} ^ {\ inf ty} (- 1) ^ {k} (q (m)) ^ {k ^ {2}} \ cos \ left ({\ frac {\ pi zk} {K (m)}} \ right) \ right) }

{\ displaystyle \ theta _ {n} (z, m) = {\ frac {\ sqrt {2 \ pi}} {2 (1-м) ^ {1/4} {\ sqrt {K (m)}}}} \, \, \ left (1 + 2 \ sum _ {k = 1} ^ {\ infty} (- 1) ^ {k} (q (m)) ^ {k ^ {2}} \ cos \ left ({\ frac {\ pi zk} {K (m)}} \ right) \ справа)}

θ s (z, m) = 2 π q (m) 1/4 m 1/4 (1 - m) 1/4 K (m) ∑ k = 0 ∞ (- 1) k (q ( м)) К (К + 1) грех ⁡ ((2 К + 1) π Z 2 К (м)) {\ Displaystyle \ theta _ {s} (г, м) = {\ гидроразрыва {{\ sqrt {2 \ pi}} \, q (m) ^ {1/4}} {m ^ {1/4} (1-m) ^ {1/4} {\ sqrt {K (m)}}}} \, \, \ sum _ {k = 0} ^ {\ infty} (- 1) ^ {k} (q (m)) ^ {k (k + 1)} \ sin \ left ({\ frac {(2k + 1) \ pi z} {2K (m)}} \ right)}

{\ displaystyle \ theta _ {s} (z, m) = {\ frac {{\ sqrt {2 \ pi}} \, q (м) ^ {1/4}} {m ^ {1/4} (1-м) ^ {1/4} {\ sqrt {K (м) }}}} \, \, \ sum _ {k = 0} ^ {\ infty} (- 1) ^ {k} (q (m)) ^ {k (k + 1)} \ sin \ left ({ \ frac {(2k + 1) \ pi z} {2K (m)}} \ right)}

где: K (m) - полный эллиптический интеграл первого рода, K '(m) = K ( 1-m), и $q (m) = e - π K '(m) / K (m) {\ displaystyle q (m) = e ^ {- \ pi K' (m) / K (m)}}$ $q(m)=e^{-\pi K'(m)/K(m)}$ - эллиптический ном.

Обратите внимание, что функции θ p (z, m) иногда определяются в терминах числа q (m) и записываются как θ p (z, q) (например, NIST). Функции также могут быть записаны в терминах параметра τ θ p (z | τ), где $q = ei π τ {\ displaystyle q = e ^ {i \ pi \ tau}}$ $q = e ^ {{i \ pi \ tau}}$ .

Содержание

1 Связь с другими функциями
2 Примеры
3 Симметрия
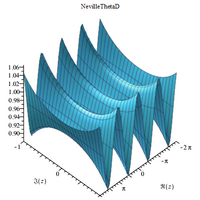
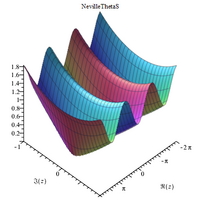
4 Сложные трехмерные графики
5 Реализация
6 Примечания
7 Ссылки

Связь с другими функциями

Тета-функции Невилля могут быть выражены через тета-функции Якоби

θ s (z | τ) = θ 23 (0 | τ) θ 1 (z ′ | τ) / θ 1 ′ (0 | τ) {\ displaystyle \ theta _ {s} (z | \ tau) = \ theta _ {23} (0 | \ tau) \ theta _ {1} (z '| \ tau) / \ theta' _ {1} (0 | \ тау)}

\theta _{s}(z|\tau)=\theta _{23}(0|\tau)\theta _{1}(z'|\tau)/\theta '_{1}(0|\tau)

θ c (z | τ) = θ 2 (z ′ | τ) / θ 2 (0 | τ) {\ displaystyle \ theta _ {c} (z | \ tau) = \ theta _ {2} (z '| \ tau) / \ theta _ {2} (0 | \ tau)}

\theta _{c}(z|\tau)=\theta _{2}(z'|\tau)/\theta _{2}(0|\tau)

θ n (z | τ) = θ 4 (z ′ | τ) / θ 4 (0 | τ) {\ displaystyle \ theta _ {n} (z | \ tau) = \ theta _ {4} (z '| \ tau) / \ theta _ {4} (0 | \ tau) }

\theta _{n}(z|\tau)=\theta _{4}(z'|\tau)/\theta _{4}(0|\tau)

θ d (z | τ) = θ 3 (z ′ | τ) / θ 3 (0 | τ) {\ displaystyle \ theta _ {d} (z | \ tau) = \ theta _ {3} (z '| \ tau) / \ theta _ {3} (0 | \ tau)}

\theta _{d}(z|\tau)=\theta _{3}(z'|\tau)/\theta _{3}(0|\tau)

где $z ′ = z / θ 3 (0 | τ) 2 {\ displaystyle z '= z / \ theta _ {3} (0 | \ tau) ^ {2}}$ $z'=z/\theta _{3}(0|\tau)^{2}$ .

Тэта-функции Невилля связаны с эллиптическими функциями Якоби. Если pq (u, m) - эллиптическая функция Якоби (p и q - одно из s, c, n, d), то

pq ⁡ (u, m) = θ p (u, m) θ q ( u, m) {\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {p} (u, m)} {\ theta _ {q} (u, m)}}}

{\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {p} (u, m)} {\ theta _ {q} (u, m)}}}

Примеры

Подставьте z = 2,5, m = 0,3 в приведенные выше определения тета-функций Невилля (используя Maple ), как только получите следующее (в соответствии с результатами математики вольфрамма).

$θ c (2,5, 0,3) = - 0,65900466676738154967 {\ displaystyle \ theta _ {c} (2.5,0.3) = - 0,65900466676738154967}$ $\ theta _ {c} (2.5,0.3) = - 0,65900466676738154967$
$θ d (2,5, 0,3) = 0,95182196661267561994 {\ displaystyle \ theta _ { d} (2.5,0.3) = 0.95182196661267561994}$ $\ theta _ {d} (2.5,0.3) = 0.95182196661267561994$
$θ n (2.5, 0.3) = 1.0526693354651613637 {\ displaystyle \ theta _ {n} (2.5,0.3) = 1.0526693354651613637}$ $\ theta _ {n} (2.5,0.3) = 1.0526693354651613637$
$θ s (2.5, 0.3) = 0.82086879524530400536 {\ displaystyle \ theta _ {s} (2.5,0.3) = 0.82086879524530400536}$ $\ theta _ {s} (2.5,0.3) = 0.82086879524530400536$

Симметрия

$θ c (z, m) = θ c (- z, m) {\ displaystyle \ theta _ {c} (z, m) = \ theta _ {c} (- z, m)}$ $\ theta _ {c} (z, m) = \ theta _ {c} (- z, m)$
$θ d (z, m) = θ d (- z, m) {\ displaystyle \ theta _ {d} (z, m) = \ theta _ {d} (- z, m)}$ $\ theta _ {d} (z, m) = \ theta _ {d} (- z, m)$
$θ n (z, m) = θ n (- z, m) {\ displaystyle \ theta _ {N} (z, m) = \ theta _ {n} (- z, m)}$ $\ theta _ {n} (z, m) = \ theta _ {n} (- z, m)$
$θ s (z, m) = - θ s (- z, m) {\ displaystyle \ theta _ {s } (z, m) = - \ theta _ {s} (- z, m)}$ $\ theta _ {s} (z, m) = - \ theta _ {s} ( -z, m)$

Сложные трехмерные графики

Реализация

NetvilleThetaC [z, m], NevilleThetaD [z, m], NevilleThetaN [z, m] и NevilleThetaS [z, m] - встроенные функции Mathematica В Maple таких функций нет.

Примечания

Ссылки

Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
Невилл, Э. Х. (Эрик Гарольд) (1944). Эллиптические функции Якоби. Oxford Clarendon Press.
Вайсштейн, Эрик У. «Невилль Тета-функции». MathWorld.