Войти
Алгоритмы слияния - это семейство алгоритмов, которые принимают несколько отсортированных списков в качестве входных данных и создают один список в качестве выходных данных, содержащий все элементы входных списков в отсортированном порядке. Эти алгоритмы используются в качестве подпрограмм в различных алгоритмах сортировки, наиболее известный из которых - сортировка слиянием.
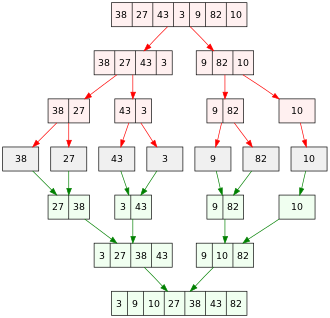Пример сортировки слиянием Алгоритм слияния играет решающую роль в алгоритме сортировки слиянием, алгоритме сортировки на основе сравнения. Концептуально алгоритм сортировки слиянием состоит из двух шагов:
Алгоритм слияния многократно используется в алгоритме сортировки слиянием.
Пример сортировки слиянием приведен на иллюстрации. Он начинается с несортированного массива из 7 целых чисел. Массив разделен на 7 разделов; каждый раздел содержит 1 элемент и сортируется. Затем отсортированные разделы объединяются для создания более крупных отсортированных разделов, пока не останется 1 раздел, отсортированный массив.
Объединение двух отсортированных списков в один может быть выполнено за линейное время и линейное или постоянное пространство (в зависимости от модели доступа к данным). Следующий псевдокод демонстрирует алгоритм, который сливается входные списки (либо связанные списки или массивы ) и Б в новый список C. Функция головки дает первый элемент списка; «удаление» элемента означает удаление его из списка, обычно путем увеличения указателя или индекса.
algorithm merge(A, B) is inputs A, B : list returns list C := new empty list while A is not empty and B is not empty do if head(A) ≤ head(B) then append head(A) to C drop the head of A else append head(B) to C drop the head of B // By now, either A or B is empty. It remains to empty the other input list. while A is not empty do append head(A) to C drop the head of A while B is not empty do append head(B) to C drop the head of B return C
Когда входы представляют собой связанные списки, этот алгоритм может быть реализован для использования только постоянного количества рабочего пространства; указатели в узлах списков могут быть повторно использованы для бухгалтерского учета и для построения окончательного объединенного списка.
В алгоритме сортировки слиянием, эта подпрограмма, как правило, используется для объединения двух суб-массивов A [lo..mid], А [середина + 1..hi] из одного массива A. Это можно сделать, скопировав подмассивы во временный массив, а затем применив алгоритм слияния, описанный выше. Выделения временного массива можно избежать, но за счет скорости и простоты программирования. Были разработаны различные алгоритмы слияния на месте, иногда приносящие в жертву линейную привязку по времени для создания алгоритма O ( n log n) ; см. Сортировку слиянием § Варианты для обсуждения.
k -way слияние обобщает двоичное слияние для произвольного числа k отсортированных входных списков. Приложения k- way слияния возникают в различных алгоритмах сортировки, включая сортировку по терпению и внешний алгоритм сортировки, который делит входные данные на k = 1/M- 1 блок, который помещается в памяти, сортирует их один за другим, а затем объединяет эти блоки.
Существует несколько решений этой проблемы. Наивное решение - сделать цикл по k спискам, чтобы каждый раз выбирать минимальный элемент, и повторять этот цикл, пока все списки не станут пустыми:
В худшем случае этот алгоритм выполняет ( k −1) ( n -k/2) сравнения элементов для выполнения своей работы, если в списках всего n элементов. Его можно улучшить, сохранив списки в очереди приоритетов ( min-heap ) с ключом их первого элемента:
Поиск следующего наименьшего элемента для вывода (find-min) и восстановление порядка кучи теперь можно выполнить за время O (log k) (точнее, 2⌊log k ⌋ сравнений), а полную проблему можно решить за O ( п лог к) время (приблизительно 2 л ⌊log K ⌋ сравнения).
Третий алгоритм решения проблемы - это решение « разделяй и властвуй», основанное на алгоритме двоичного слияния:
Когда входные списки для этого алгоритма упорядочены по длине, сначала самые короткие, для этого требуется меньше n log k ⌉ сравнений, т. Е. Меньше половины числа, используемого алгоритмом на основе кучи; на практике он может быть таким же быстрым или медленным, как алгоритм на основе кучи.
Параллельная версия алгоритма двоичного слияния может служить в качестве строительного блока в параллельной сортировки слиянием. Следующий псевдокод демонстрирует этот алгоритм в параллельном стиле « разделяй и властвуй» (адаптированный из Кормена и др.). Он работает на двух отсортированных массивов A и B и записывает отсортированный вывод в массив C. Обозначение A [i... j] обозначает часть A от индекса i до j, исключая.
algorithm merge(A[i...j], B[k...ℓ], C[p...q]) is inputs A, B, C : array i, j, k, ℓ, p, q : indices let m = j - i, n = ℓ - k if m lt; n then swap A and B // ensure that A is the larger array: i, j still belong to A; k, ℓ to B swap m and n if m ≤ 0 then return // base case, nothing to merge let r = ⌊(i + j)/2⌋ let s = binary-search(A[r], B[k...ℓ]) let t = p + (r - i) + (s - k) C[t] = A[r] in parallel do merge(A[i...r], B[k...s], C[p...t]) merge(A[r+1...j], B[s...ℓ], C[t+1...q])
Алгоритм работает путем разделения A или B, в зависимости от того, что больше, на (почти) равные половины. Затем он разбивает другой массив на часть со значениями, меньшими, чем средняя точка первого, и часть с большими или равными значениями. (В бинарном поиске возвращается подпрограмма индекс в B, где [ г ] был бы, если бы это было в B, что это всегда число между к и л.) Наконец, каждая пара половинок сливается рекурсивно, и поскольку рекурсивные вызовы независимы друг от друга, их можно делать параллельно. Гибридный подход, в котором для базового случая рекурсии используется последовательный алгоритм, на практике показывает хорошие результаты.
Работа выполняется с помощью алгоритма для двух массивов, занимающих в общей сложности п элементов, то есть, время работы в серийную версию этого, является О ( п). Это является оптимальным, так как п элементы должны быть скопированы в C. Чтобы вычислить диапазон алгоритма, необходимо вывести отношение повторяемости. Поскольку два рекурсивных вызова слияния выполняются параллельно, необходимо учитывать только более затратный из двух вызовов. В худшем случае максимальное количество элементов в одном из рекурсивных вызовов не превышает максимума, поскольку массив с большим количеством элементов идеально разделяется пополам. Добавляя стоимость двоичного поиска, мы получаем это повторение как верхнюю границу:
Решение состоит в том, что на идеальной машине с неограниченным количеством процессоров требуется столько времени.
Примечание. Процедура нестабильна : если равные элементы разделены разделением A и B, они будут чередоваться в C ; также обмен местами A и B уничтожит порядок, если одинаковые элементы распределены между обоими входными массивами. В результате при использовании для сортировки этот алгоритм производит нестабильную сортировку.
Некоторые компьютерные языки предоставляют встроенную или библиотечную поддержку для объединения отсортированных коллекций.
В C ++ «сек Стандартная библиотека шаблонов имеет функцию зЬй:: слияния, который объединяет два сортируются диапазоны итераторы и зЬй:: inplace_merge, который объединяет два последовательных отсортированных диапазонов в месте. Кроме того, класс std:: list (связанный список) имеет собственный метод слияния, который объединяет другой список в себя. Тип объединяемых элементов должен поддерживать оператор «меньше» ( lt;) или должен быть предоставлен с настраиваемым компаратором.
C ++ 17 допускает различные политики выполнения, а именно последовательное, параллельное и неупорядоченное параллельное выполнение.
Python «s стандартная библиотека (с 2.6) также имеет слияние функцию в heapq модуле, который принимает несколько отсортированных итерируемый, и объединяют их в один итератор.
