Янга – Лапласа uation

Оптические тензиометры используют уравнение Юнга-Лапласа для автоматического определения поверхностного натяжения жидкости на основе формы висячей капли.

В физике, уравнение Юнга – Лапласа () является нелинейным уравнением в частных производных, которое описывает капиллярное давление разница между двумя статическими жидкостями, такими как вода и воздух на границе раздела фаз, из-за явления поверхностного натяжения или натяжение стенки, хотя использование последнего применимо только в том случае, если предполагается, что стена очень тонкая. Уравнение Юнга – Лапласа связывает перепад давления с формой поверхности или стенки, и это фундаментально важно при изучении статических капиллярных поверхностей. Это утверждение баланса нормального напряжения для статических жидкостей, встречающихся на границе раздела, где граница раздела рассматривается как поверхность (нулевая толщина):

$\Delta \; p\; =\; -\; \gamma \; \nabla \; \cdot \; N\; ^\; знак\; равно\; -\; \gamma \; H\; е\; знак\; равно\; -\; \gamma \; (1\; R\; 1\; +\; 1\; R\; 2)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; Delta\; p\; =\; -\; \backslash \; gamma\; \backslash \; nabla\; \backslash \; cdot\; \{\backslash \; hat\; \{n\}\}\; \backslash \backslash \; =\; -\; \backslash \; gamma\; H\_\; \{f\}\; \backslash \backslash \; =\; -\; \backslash \; gamma\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{R\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{2\}\}\}\; \backslash \; right)\; \backslash \; end\; \{выровнено\}\}\}$

где $\Delta \; p\; \{\backslash \; displaystyle\; \backslash \; Delta\; p\}$- это давление Лапласа, разность давлений на границе раздела текучей среды (внешнее давление минус внутреннее давление), $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$- это поверхностное натяжение (или натяжение стенки ), $n\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{n\}\}\}$- нормаль, указывающая на поверхность, $H\; f\; \{\backslash \; displaystyle\; H\_\; \{f\}\}$- среднее значение кривизна (определена в разделе «Средняя кривизна в гидромеханике») и $R\; 1\; \{\backslash \; displaystyle\; R\_\; \{1\}\}$и $R\; 2\; \{\backslash \; displaystyle\; R\_\; \{\; 2\}\}$- главные радиусы кривизны. Обратите внимание, что учитывается только нормальное напряжение, поскольку было показано, что статическая граница раздела возможна только при отсутствии касательного напряжения.

Уравнение названо в честь Томаса Янга, который разработал качественную теорию поверхностного натяжения в 1805 году, и Пьера-Симона Лапласа, завершившего математическое описание следующим образом год. Иногда его также называют уравнением Юнга – Лапласа – Гаусса, поскольку Карл Фридрих Гаусс объединил работы Юнга и Лапласа в 1830 году, выведя как дифференциальное уравнение, так и граничные условия с использованием Иоганна Бернулли принципы виртуальной работы.

• 1 Мыльные пленки
• 2 Эмульсии
• 3 Капиллярное давление в трубке
• 4 Капиллярное действие в целом
  • 4.1 Осесимметричные уравнения
• 5 Применение в медицине
• 6 История
• 7 Ссылки
• 8 Библиография
• 9 Внешние ссылки

Если разница давлений равна нулю, как в мыле пленка без силы тяжести, граница раздела примет форму минимальной поверхности.

Уравнение также объясняет энергию, необходимую для создания эмульсии. Чтобы сформировать маленькие, сильно изогнутые капли эмульсии, требуется дополнительная энергия, чтобы преодолеть большое давление, возникающее из-за их малого радиуса.

Давление Лапласа, которое больше для более мелких капель, вызывает диффузию молекул из мельчайших капель в эмульсии и вызывает укрупнение эмульсии за счет созревания Оствальда.

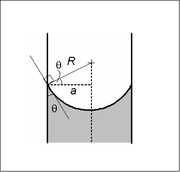Сферический мениск с углом смачивания менее 90 °

В достаточно узкой (т. Е. С низким числом Бонда ) трубке круглого сечения (радиус а) граница раздела между двумя жидкостями образует мениск, который является частью поверхности сферы с радиусом R. Скачок давления на этой поверхности связан с радиусом и поверхностным натяжением γ соотношением

$\Delta \; p\; =\; 2\; \gamma \; R.\; \{\backslash \; displaystyle\; \backslash \; Delta\; p\; =\; \{\backslash \; frac\; \{2\; \backslash \; gamma\}\; \{R\}\}.\}$

Это можно показать, записав уравнение Юнга – Лапласа в сферической форме с граничным условием краевого угла а также заданное граничное условие по высоте, скажем, на дне мениска. Решение представляет собой часть сферы, и решение будет существовать только для указанной выше разницы давлений. Это важно, потому что нет другого уравнения или закона для определения разности давлений; наличие решения для одного конкретного значения перепада давления предписывает это.

Радиус сферы будет зависеть только от угла контакта, θ, который, в свою очередь, зависит от точных свойств жидкостей и материала контейнера, с которым эти жидкости контактируют / взаимодействуют:

$R\; =\; a\; cos\; \; \theta \; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{a\}\; \{\backslash \; cos\; \backslash \; theta\}\}\}$

, так что перепад давления может быть записан как:

$\Delta \; p\; =\; 2\; \gamma \; cos\; \; \theta \; a.\; \{\backslash \; displaystyle\; \backslash \; Delta\; p\; =\; \{\backslash \; frac\; \{2\; \backslash \; gamma\; \backslash \; cos\; \backslash \; theta\}\; \{a\}\}.\}$

Иллюстрация капиллярного подъема. Красный = угол контакта менее 90 °; синий = угол контакта больше 90 °

Для поддержания гидростатического равновесия индуцированное капиллярное давление уравновешивается изменением высоты h, которое может быть положительным или отрицательным. в зависимости от того, меньше или больше угол смачивания 90 °. Для жидкости с плотностью ρ:

$h\; =\; 2\; \gamma \; cos\; \; \theta \; \rho \; g\; a.\; \{\backslash \; displaystyle\; h\; =\; \{\backslash \; frac\; \{2\; \backslash \; gamma\; \backslash \; cos\; \backslash \; theta\}\; \{\backslash \; rho\; ga\}\}.\}$

- где g - ускорение свободного падения. Это иногда называют законом Джурина или высотой Джурина в честь Джеймса Джурина, изучавшего эффект в 1718 году.

Для наполненной водой стеклянной трубки в воздухе на уровне моря :

γ = 0,0728 Дж / м при 20 ° C	θ = 20 ° (0,35 рад )
ρ = 1000 кг / м	g = 9,8 м / с

- поэтому высота водяного столба определяется по формуле:

$h\; \approx \; 1,4\; \times \; 10\; -\; 5\; a\; \{\backslash \; displaystyle\; h\; \backslash \; приблизительно\; \{\{1,4\; \backslash \; times\; 10\; ^\; \{-\; 5\}\}\; \backslash \; over\; a\}\}$m.

Таким образом, для трубки шириной 2 мм (радиус 1 мм) вода поднимется на 14 мм. Однако для капиллярной трубки с радиусом 0,1 мм, вода поднимется на 14 см (около 6 дюймов ).

В общем случае для свободной поверхности и там, где имеется приложенное «избыточное давление», Δp, на границе раздела в равновесии, существует баланс между приложенным давлением, гидростатическим давлением и эффектами поверхностного натяжения. Уравнение Юнга – Лапласа принимает следующий вид:

$\Delta \; p\; =\; \rho \; gh\; -\; \gamma \; (1\; R\; 1\; +\; 1\; R\; 2)\; \{\backslash \; displaystyle\; \backslash \; Delta\; p\; =\; \backslash \; rho\; gh-\; \backslash \; gamma\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{R\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{2\}\}\}\; \backslash \; right)\}$

Уравнение может быть безразмерным с точки зрения его характерного масштаба длины, длины капилляра :

$L\; c\; =\; \gamma \; \rho \; g,\; \{\backslash \; displaystyle\; L\_\; \{c\}\; =\; \{\backslash \; sqrt\; \{\; \backslash \; frac\; \{\backslash \; gamma\}\; \{\backslash \; rho\; g\}\}\},\}$

- и характеристическое давление :

$pc\; =\; \gamma \; L\; c\; =\; \gamma \; \rho \; g.\; \{\backslash \; displaystyle\; p\_\; \{c\}\; =\; \{\backslash \; frac\; \{\backslash \; gamma\}\; \{L\_\; \{c\}\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; gamma\; \backslash \; rho\; g\}\}.\}$

Для чистой воды при стандартной температуре и давлении, длина капилляра составляет ~ 2 mm.

Безразмерное уравнение тогда принимает следующий вид:

$h\; \ast \; -\; \Delta \; p\; \ast \; =\; (1\; R\; 1\; \ast \; +\; 1\; R\; 2\; \ast ).\; \{\backslash \; displaystyle\; h\; ^\; \{*\}\; -\; \backslash \; Delta\; p\; ^\; \{*\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{\{R\_\; \{1\}\}\; ^\; \{*\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{\{R\_\; \{\; 2\}\}\; ^\; \{*\}\}\}\; \backslash \; right).\}$

Таким образом, форма поверхности определяется только одним параметром: избыточное давление жидкости Δp, а масштаб поверхности определяется значением длина капилляра . Решение уравнения требует начального условия для положения и уклона поверхности в начальной точке.

Висячая капля образуется при избыточном давлении Δp = 3 и начальном состоянии r 0 = 10, z 0 = 0, dz / dr = 0 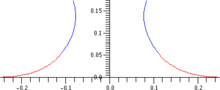A жидкий мостик создается для избыточного давления Δp = 3,5 и начальных условий r 0 = 0,25, z 0 = 0, dz / dr = 0

Осесимметричные уравнения

(безразмерная) форма r (z) осесимметричной поверхности может быть найдена путем замены общих выражений для кривизны, чтобы получить гидростатический Уравнения Юнга – Лапласа :

$r\; ″\; (1\; +\; r\; \prime \; 2)\; 3\; 2\; -\; 1\; r\; (z)\; 1\; +\; r\; \prime \; 2\; =\; z\; -\; \Delta \; p\; \ast \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{r\; \text{'}\text{'}\}\; \{(1\; +\; r\; \text{'}^\; \{2\})\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{r\; (z)\; \{\backslash \; sqrt\; \{1\; +\; r\text{'}\; ^\; \{2\}\}\}\}\}\; =\; z-\; \backslash \; Delta\; p\; ^\; \{*\}\}$

$z\; ″\; (1\; +\; z\; \prime \; 2)\; 3\; 2\; +\; z\; \prime \; r\; (1\; +\; z\; \prime \; 2)\; 1\; 2\; =\; \Delta \; p\; \ast \; -\; z\; (r).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{z\; \text{'}\text{'}\}\; \{(1\; +\; z\; \text{'}^\; \{2\})\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\}\; +\; \{\backslash \; frac\; \{z\text{'}\}\; \{r\; (1\; +\; z\; \text{'}\; ^\; \{2\})\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}\; =\; \backslash \; Delta\; p\; ^\; \{*\}\; -\; z\; (r).\}$

В медицине его часто называют законом Лапласа, используемым в контексте физиологии сердечно-сосудистой системы, а также физиологии дыхания, хотя последнее использование часто ошибочны.

Фрэнсис Хоксби провел некоторые из самых ранних наблюдений и экспериментов в 1709 году, и они были повторены в 1718 году Джеймсом Юрином, который заметил, что высота жидкости в капиллярной колонке зависела только от площади поперечного сечения на поверхности, а не от любых других размеров колонки.

Томас Янг заложил основы уравнения в своей статье 1804 года An Essay on the Cohesion of Fluids, где он описал принципы, управляющие контактом между жидкостями (наряду со многими другими аспектами поведения жидкости). Пьер Симон Лаплас продолжил это в Mécanique Céleste с формальным математическим описанием, приведенным выше, которое воспроизводило в символических терминах отношения, описанные ранее Янгом.

Лаплас принял идею, предложенную Хоксби в его книге «Физико-механические эксперименты» (1709 г.), о том, что это явление возникло из-за силы притяжения, незаметной на ощутимых расстояниях. Часть, которая касается действия твердого вещества на жидкость и взаимного действия двух жидкостей, не была полностью проработана, но в конечном итоге была завершена Карлом Фридрихом Гауссом. Франц Эрнст Нойман (1798-1895) позже внес несколько подробностей.

• Максвелл, Джеймс Клерк ; Стратт, Джон Уильям (1911). «Капиллярное действие». В Чисхолме, Хью (ред.). Британская энциклопедия. 5(11-е изд.). Издательство Кембриджского университета. С. 256–275.
• Бэтчелор, Г. К. (1967) Введение в динамику жидкости, Cambridge University Press
• Джурин, Дж. (1716). «Отчет о некоторых экспериментах, показанных Королевскому обществу; с исследованием причины подъема и суспендирования воды в капиллярных трубках». Философские труды Королевского общества. 30 (351–363): 739–747. doi : 10.1098 / rstl.1717.0026. S2CID 186211806.
• Тадрос Т.Ф. (1995) Поверхностно-активные вещества в агрохимикатах, серия Surfactant Science, том 54, Деккер

Измерение поверхностного натяжения с помощью уравнения Юнга-Лапласа