Скорость

Вектор, измеряющий скорость изменения положения с течением времени движущейся точки

Скорость
При изменении направления пока гоночные автомобили едут по кривой трассе, их скорость не постоянна.
Общие символы	v, v, v →
Другие единицы	миль / ч, фут / с
В базовых единицах СИ	m /s
Размер	LT

скорость объекта - это скорость изменения его положения по отношению к системе отсчета и является функцией времени. Скорость эквивалентна заданию скорости объекта и направления движения (например, 60 км / ч на север). Скорость - это фундаментальное понятие в кинематике, ветви классической механики, которая описывает движение тел.

Скорость - это физический вектор величина ; для его определения необходимы и величина, и направление. scalar абсолютное значение (величина ) скорости называется скоростью, являясь согласованной производной единицей, величина которой измеряется в SI (метрической системе ) как метров в секунду (м / с) или как базовая единица СИ (м⋅с). Например, «5 метров в секунду» - это скаляр, а «5 метров в секунду на восток» - это вектор. Если есть изменение скорости, направления или и того, и другого, то объект имеет изменяющуюся скорость и считается, что он испытывает ускорение.

Содержание

• 1 Постоянная скорость в зависимости от ускорения
• 2 Разница между скоростью и скорость
• 3 Уравнение движения
  • 3.1 Средняя скорость
  • 3.2 Мгновенная скорость
  • 3.3 Связь с ускорением
    • 3.3.1 Постоянное ускорение
  • 3.4 Величины, зависящие от скорости
• 4 Относительные скорость
  • 4.1 Скалярные скорости
• 5 Полярные координаты
• 6 См. также
• 7 Примечания
• 8 Ссылки
• 9 Внешние ссылки

Постоянная скорость в зависимости от ускорения

Чтобы иметь постоянная скорость, объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление заставляет объект двигаться по прямой траектории, поэтому постоянная скорость означает движение по прямой с постоянной скоростью.

Например, автомобиль, движущийся со скоростью 20 километров в час по круговой траектории, имеет постоянную скорость, но не имеет постоянной скорости, потому что его направление меняется. Следовательно, считается, что автомобиль испытывает ускорение.

Разница между скоростью и скоростью

Кинематические величины классической частицы: масса m, положение r, скорость v, ускорение a.

Скорость, скаляр величина вектора скорости, обозначает только скорость движения объекта.

Уравнение движения

Средняя скорость

Скорость определяется как скорость изменения положения относительно времени, которое также может называться мгновенной скоростью, чтобы подчеркнуть отличие от средней скорости. В некоторых приложениях может потребоваться «средняя скорость» объекта, то есть постоянная скорость, которая обеспечит такое же результирующее смещение, что и переменная скорость в том же интервале времени, v (t), за некоторый промежуток времени Δt. Среднюю скорость можно рассчитать как:

$v\; ¯\; =\; \Delta \; x\; \Delta \; t.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; bar\; \{v\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; Delta\; \{\backslash \; boldsymbol\; \{x\}\}\}\; \{\backslash \; Delta\; \{\backslash \; mathit\; \{t\}\}\}\}.\}$

Средняя скорость всегда меньше или равна средней скорости объекта. Это можно увидеть, осознав, что, хотя расстояние всегда строго увеличивается, смещение может увеличиваться или уменьшаться по величине, а также изменять направление.

В терминах графика смещения-времени (x в зависимости от t) мгновенную скорость (или просто скорость) можно представить как наклон касательной к кривой в любом точка, а средняя скорость - как наклон секущей линии между двумя точками с координатами t, равными границам периода времени для средней скорости.

Средняя скорость такая же, как и скорость, усредненная по времени, то есть ее средневзвешенное значение по времени, которое может быть вычислено как интеграл скорости от времени:

$v\; ¯\; =\; 1\; t\; 1\; -\; t\; 0\; \int \; t\; 0\; t\; 1\; v\; (t)\; dt,\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; bar\; \{v\}\}\}\; =\; \{1\; \backslash \; over\; t\_\; \{1\}\; -t\_\; \{0\}\}\; \backslash \; int\; \_\; \{t\_\; \{\; 0\}\}\; ^\; \{t\_\; \{1\}\}\; \{\backslash \; boldsymbol\; \{v\}\}\; (t)\; \backslash \; dt,\}$

где мы можем идентифицировать

$\Delta \; x\; =\; \int \; t\; 0\; t\; 1\; v\; (t)\; dt\; \{\backslash \; displaystyle\; \backslash \; Delta\; \{\backslash \; boldsymbol\; \{x\}\}\; =\; \backslash \; int\; \_\; \{t\_\; \{0\}\}\; ^\; \{t\_\; \{1\}\}\; \{\backslash \; boldsymbol\; \{v\}\}\; (t)\; \backslash \; dt\}$

и

$\Delta \; t\; =\; t\; 1\; -\; т\; 0.\; \{\backslash \; displaystyle\; \backslash \; Delta\; t\; =\; t\_\; \{1\}\; -t\_\; \{0\}.\}$

Мгновенная скорость

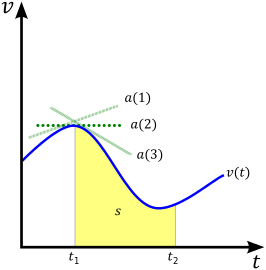Пример графика зависимости скорости от времени и взаимосвязь между скоростью v на оси y -ось, ускорение a (три зеленые касательные линии представляют значения ускорения в разных точках вдоль кривой) и смещение s (желтый площадь под кривой.)

Если мы рассматриваем v как скорость и x как вектор смещения (изменения положения), то мы можем выразить (мгновенное) скорость частицы или объекта в любой конкретный момент времени t как производная положения по времени:

$v\; =\; lim\; \Delta \; t\; \to \; 0\; \Delta \; x\; \Delta \; t\; =\; dxdt.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; =\; \backslash \; lim\; \_\; \{\{\backslash \; Delta\; t\}\; \backslash \; to\; 0\}\; \{\backslash \; frac\; \{\backslash \; Delta\; \{\backslash \; boldsymbol\; \{x\}\}\}\; \{\backslash \; Delta\; t\}\}\; =\; \{\backslash \; frac\; \{d\; \{\backslash \; boldsymbol\; \{x\}\}\}\; \{d\; \{\backslash \; mathit\; \{t\}\}\}\}.\}$

Из этого производного уравнения в одномерном случае видно, что площадь под действием скорости в зависимости от времени (v в зависимости от графика t) - смещение, x . С точки зрения вычислений, интеграл функции скорости v (t) является функцией смещения x (t). На рисунке это соответствует желтой области под кривой, обозначенной s(s(альтернативное обозначение смещения).

$х\; =\; \int \; v\; d\; t.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{x\}\}\; =\; \backslash \; int\; \{\backslash \; boldsymbol\; \{v\}\}\; \backslash \; d\; \{\backslash \; mathit\; \{t\}\}.\}$

Поскольку производная позиции по времени дает изменение позиции ( в метрах ), разделенных на изменение во времени (в секундах ), скорость измеряется в метрах в секунду (м / с). Хотя концепция мгновенной скорости на первый взгляд может показаться нелогичной, ее можно рассматривать как скорость, с которой объект продолжал бы двигаться, если бы в этот момент он прекратил ускоряться.

Связь с ускорением

Хотя скорость определяется как скорость изменения положения, часто обычно начинают с выражения для ускорения объекта. Как видно из трех зеленых касательных линий на рисунке, мгновенное ускорение объекта в определенный момент времени представляет собой угол наклона касательной линии к кривой v (t) график в этой точке. Другими словами, ускорение определяется как производная скорости по времени:

$a\; =\; d\; v\; d\; t.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{a\}\}\; =\; \{\backslash \; frac\; \{d\; \{\backslash \; boldsymbol\; \{v\}\}\}\; \{d\; \{\backslash \; mathit\; \{t\}\}\}\}.\}$

Отсюда мы можем получить выражение для скорости как площадь под графиком зависимости ускорения от времени a (t). Как и выше, это делается с использованием концепции интеграла:

$v\; =\; \int \; a\; d\; t.\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; =\; \backslash \; int\; \{\backslash \; boldsymbol\; \{a\}\}\; \backslash \; d\; \{\backslash \; mathit\; \{t\}\}.\}$

Постоянное ускорение

В особом случае постоянного ускорения Скорость может быть изучена с помощью уравнений сувата. Считая a равным некоторому произвольному постоянному вектору, легко показать, что

$v\; =\; u\; +\; at\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; =\; \{\backslash \; boldsymbol\; \{u\}\}\; +\; \{\backslash \; boldsymbol\; \{a\}\}\; t\}$

с v в качестве скорости в момент времени t и u в качестве скорости в момент времени t = 0. Комбинируя это уравнение с уравнение Сувата x= ut + a t / 2, можно связать смещение и среднюю скорость как

$x\; =\; (u\; +\; v)\; 2\; t\; =\; v\; ¯\; t\; \{\backslash \; displaystyle\; \{\; \backslash \; boldsymbol\; \{x\}\}\; =\; \{\backslash \; frac\; \{(\{\backslash \; boldsymbol\; \{u\}\}\; +\; \{\backslash \; boldsymbol\; \{v\}\})\}\; \{2\}\}\; \{\backslash \; mathit\; \{t\}\}\; =\; \{\backslash \; boldsymbol\; \{\backslash \; bar\; \{v\}\; \}\}\; \{\backslash \; mathit\; \{t\}\}\}$.

Также можно вывести выражение для скорости, не зависящее от времени, известное как уравнение Торричелли, следующим образом:

$v\; 2\; =\; v\; \cdot \; v\; знак\; равно\; (u\; +\; at)\; \cdot \; (u\; +\; at)\; =\; u\; 2\; +\; 2\; t\; (a\; \cdot \; u)\; +\; a\; 2\; t\; 2\; \{\backslash \; displaystyle\; v\; ^\; \{2\}\; =\; \{\backslash \; boldsymbol\; \{v\}\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{v\}\}\; =\; (\{\backslash \; boldsymbol\; \{u\}\}\; +\; \{\backslash \; boldsymbol\; \{a\}\}\; t)\; \backslash \; cdot\; (\{\backslash \; boldsymbol\; \{u\}\}\; +\; \{\backslash \; boldsymbol\; \{a\}\}\; t)\; =\; u\; ^\; \{2\}\; +\; 2t\; (\{\backslash \; boldsymbol\; \{a\}\}\; \backslash \; cdot\; \{\backslash \; bolds\; ymbol\; \{u\}\})\; +\; a\; ^\; \{2\}\; t\; ^\; \{2\}\}$

$(2\; a)\; \cdot \; x\; =\; (2\; a)\; \cdot \; (ut\; +\; 1\; 2\; at\; 2)\; =\; 2\; t\; (a\; \cdot \; u)\; +\; a\; 2\; T\; 2\; =\; v\; 2\; -\; U\; 2\; \{\backslash \; displaystyle\; (2\; \{\backslash \; boldsymbol\; \{a\}\})\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{x\}\}\; =\; (2\; \{\backslash \; boldsymbol\; \{a\}\})\; \backslash \; cdot\; (\{\backslash \; boldsymbol\; \{\; u\}\}\; t\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; boldsymbol\; \{a\}\}\; t\; ^\; \{2\})\; =\; 2t\; (\{\backslash \; boldsymbol\; \{a\}\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{u\}\})\; +\; a\; ^\; \{2\}\; t\; ^\; \{2\}\; =\; v\; ^\; \{2\}\; -u\; ^\; \{2\}\}$

$\therefore \; v\; 2\; =\; u\; 2\; +\; 2\; (a\; \cdot \; x)\; \{\backslash \; displaystyle\; \backslash ,\; следовательно,\; v\; ^\; \{2\}\; =\; u\; ^\; \{2\}\; +2\; (\{\backslash \; boldsymbol\; \{a\}\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{x\}\})\}$

, где v = | v | и т. д.

Приведенные выше уравнения справедливы как для механики Ньютона, так и для специальной теории относительности. Отличия ньютоновской механики и специальной теории относительности заключаются в том, как разные наблюдатели описывают одну и ту же ситуацию. В частности, в механике Ньютона все наблюдатели соглашаются относительно значения t, а правила преобразования положения создают ситуацию, в которой все не ускоряющиеся наблюдатели описывают ускорение объекта с одинаковыми значениями. То же самое нельзя сказать о специальной теории относительности. Другими словами, можно рассчитать только относительную скорость.

Величины, которые зависят от скорости

кинетическая энергия движущегося объекта зависит от его скорости и определяется уравнением

$E\; k\; =\; 1\; 2\; mv\; 2\; \{\backslash \; displaystyle\; E\; \_\; \{\backslash \; text\; \{k\}\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; mv\; ^\; \{2\}\}$

без учета специальной теории относительности, где E k - кинетическая энергия, m - масса. Кинетическая энергия - это скалярная величина, поскольку она зависит от квадрата скорости, однако связанная с ней величина, импульс, является вектором и определяется как

$p\; =\; mv\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{p\}\; \}\; =\; m\; \{\backslash \; boldsymbol\; \{v\}\}\}$

В специальной теории относительности безразмерный фактор Лоренца появляется часто и выражается как

$\gamma \; =\; 1\; 1\; -\; v\; 2\; c\; 2\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{v\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\}\}\}\}$

где γ - Фактор Лоренца, а c - скорость света.

Скорость убегания - это минимальная скорость, необходимая баллистическому объекту для вылета из массивного тела, такого как Земля. Он представляет собой кинетическую энергию, которая при добавлении к гравитационной потенциальной энергии объекта (которая всегда отрицательна) равна нулю. Общая формула для космической скорости объекта на расстоянии r от центра планеты с массой M:

$ve\; =\; 2\; GM\; r\; =\; 2\; gr,\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; text\; \{e\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2GM\}\; \{r\}\}\}\; =\; \{\backslash \; sqrt\; \{2gr\}\},\}$

где G - Гравитационная постоянная, а g - Ускорение свободного падения. Скорость убегания от поверхности Земли составляет около 11 200 м / с, независимо от направления объекта. Это делает термин «космическая скорость» несколько неправильным, поскольку более правильным термином будет «космическая скорость»: любой объект, достигающий скорости такой величины, независимо от атмосферы, будет покидать окрестности основного тела, пока он этого не делает. t пересекаются с чем-то на своем пути.

Относительная скорость

Относительная скорость - это измерение скорости между двумя объектами, определенное в единой системе координат. Относительная скорость является фундаментальной как в классической, так и в современной физике, поскольку многие системы в физике имеют дело с относительным движением двух или более частиц. В механике Ньютона относительная скорость не зависит от выбранной инерциальной системы отсчета. Это больше не относится к специальной теории относительности, в которой скорости зависят от выбора системы отсчета.

Если объект A движется с вектором скорости v, а объект B с вектором скорости w, то скорость объекта A относительно объекта B определяется как разность двух векторов скорости:

$v\; A\; относительно\; B\; =\; v\; -\; w\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{A\; \{\backslash \; text\; \{относительно\}\}\; B\}\; =\; \{\backslash \; boldsymbol\; \{v\}\}\; -\; \{\backslash \; boldsymbol\; \{w\}\}\}$

Аналогично, относительная скорость объекта B, движущегося со скоростью w, относительно объекта A, движущегося со скоростью v, составляет:

$v\; B\; относительно\; A\; =\; w\; -\; v\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{B\; \{\backslash \; text\; \{относительно\}\}\; A\}\; =\; \{\backslash \; boldsymbol\; \{w\}\}\; -\; \{\backslash \; boldsymbol\; \{v\}\}\}$

Обычно выбирается инерциальная система отсчета, в которой последний из двух упомянутых объектов находится в покое.

Скалярные скорости

В одномерном случае скорости являются скалярами, а уравнение имеет вид:

$vrel\; =\; v\; -\; (-\; w)\; \{\backslash \; displaystyle\; \backslash ,\; v\_\; \{rel\; \}\; =\; v\; -\; (-\; w)\}$, если два объекта движутся в противоположных направлениях, или:

$vrel\; =\; v\; -\; (+\; w)\; \{\backslash \; displaystyle\; \backslash ,\; v\_\; \{rel\}\; =\; v\; -\; (+\; w)\}$, если два объекта движутся в одном направлении.

Полярные координаты

В полярных координатах двумерная скорость описывается радиальной скоростью, определяемой как составляющая скорости в направлении от или к источнику (также известная как исправленная скорость), и угловой скоростью, которая является скоростью вращение вокруг начала координат (положительные величины представляют вращение против часовой стрелки, а отрицательные величины представляют вращение по часовой стрелке в правой системе координат).

Радиальная и угловая скорости могут быть получены из декартовых векторов скорости и смещения путем разложения вектора скорости на радиальную и поперечную составляющие. Поперечная скорость - это составляющая скорости вдоль окружности с центром в начале координат.

$v\; =\; v\; T\; +\; v\; R\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; =\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{T\}\; +\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{R\}\}$

где

$v\; T\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{T\}\}$- поперечная скорость

$v\; R\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{R\}\}$- радиальная скорость.

Величина радиальной скорости - это скалярное произведение вектора скорости и единичного вектора в направлении смещения.

$v\; R\; =\; v\; \cdot \; r\; |\; г\; |\; \{\backslash \; displaystyle\; v\_\; \{R\}\; =\; \{\backslash \; frac\; \{\{\backslash \; boldsymbol\; \{v\}\}\; \backslash \; cdot\; \{\backslash \; boldsymbol\; \{r\}\}\}\; \{\backslash \; left\; |\; \{\backslash \; boldsymbol\; \{r\}\}\; \backslash \; right\; |\}\}\}$

где

$r\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{r\}\}\}$- смещение.

Величина поперечной скорости равна перекрестному произведению единичного вектора в направление смещения и вектор скорости. Это также произведение угловой скорости $\omega \; \{\backslash \; displaystyle\; \backslash \; omega\}$и величины смещения.

$v\; T\; =\; |\; r\; \times \; v\; |\; |\; г\; |\; =\; \omega \; |\; г\; |\; \{\backslash \; displaystyle\; v\_\; \{T\}\; =\; \{\backslash \; frac\; \{|\; \{\backslash \; boldsymbol\; \{r\}\}\; \backslash \; times\; \{\backslash \; boldsymbol\; \{v\}\}\; |\}\; \{|\; \{\backslash \; boldsymbol\; \{r\}\}\; |\}\}\; =\; \backslash \; omega\; |\; \{\backslash \; boldsymbol\; \{r\}\}\; |\}$

такие, что

$\omega \; =\; |\; r\; \times \; v\; |\; |\; г\; |\; 2.\; \{\backslash \; displaystyle\; \backslash \; omega\; =\; \{\backslash \; frac\; \{|\; \{\backslash \; boldsymbol\; \{r\}\}\; \backslash \; times\; \{\backslash \; boldsymbol\; \{v\}\}\; |\}\; \{|\; \{\backslash \; boldsymbol\; \{r\}\}\; |\; ^\; \{2\}\}\}.\}$

Угловой момент в скалярной форме равен массе, умноженной на расстояние до начала координат, умноженной на поперечную скорость, или, что эквивалентно, масса, умноженная на квадрат расстояния, умноженная на угловую скорость. Знаки для углового момента такие же, как и для угловой скорости.

$L\; =\; mrv\; T\; =\; mr\; 2\; \omega \; \{\backslash \; displaystyle\; L\; =\; mrv\_\; \{T\}\; =\; mr\; ^\; \{2\}\; \backslash \; omega\; \backslash ,\}$

где

$m\; \{\backslash \; displaystyle\; m\; \backslash ,\}$- масса

$r\; =\; \Vert \; r\; \Vert .\; \{\backslash \; displaystyle\; r\; =\; \backslash \; |\; \{\backslash \; boldsymbol\; \{r\}\}\; \backslash \; |.\}$

Выражение $mr\; 2\; \{\backslash \; displaystyle\; mr\; ^\; \{2\}\}$известно как момент инерции. Если силы действуют только в радиальном направлении с обратной квадратичной зависимостью, как в случае гравитационной орбиты, угловой момент постоянен, а поперечная скорость обратно пропорциональна расстоянию, угловая скорость обратно пропорциональна квадрат расстояния и скорость выметания площади постоянны. Эти отношения известны как законы движения планет Кеплера.

См. Также

• Четыре скорости (релятивистская версия скорости для пространства-времени Минковского )
• Групповая скорость
• Гиперскорость
• Фазовая скорость
• Собственная скорость (в теории относительности, с использованием времени путешественника вместо времени наблюдателя)
• Скорость (версия аддитивной скорости при релятивистских скоростях)
• Конечная скорость
• Зависимость скорости от скорости график времени

Примечания

Ссылки

• Роберт Резник и Джерл Уокер, «Основы физики», Wiley; 7-е издание (16 июня 2004 г.). ISBN 0-471-23231-9.

Внешние ссылки

Викискладе есть материалы, связанные с Velocity.

• Physicsabout.com, Speed ​​and Velocity
• Velocity and Acceleration
• Введение в механизмы (Университет Карнеги-Меллона )