Действительность (логика)

редактировать

Аргумент, вывод которого должен быть истинным, если его предпосылки

В логике, точнее в дедуктивном рассуждении, аргумент является действительным тогда и только тогда, когда он принимает форму, которая делает невозможным для посылок быть правдой, а вывод все же ложным. Для действительного аргумента не требуется иметь посылки, которые на самом деле истинны, но необходимо наличие посылок, которые, если бы они были истинными, гарантировали бы истинность вывода аргумента. Действительные аргументы должны быть четко выражены с помощью предложений, называемых правильно построенными формулами (также называемых wffs или просто формулами). достоверность аргумента - его действительность - можно проверить, доказать или опровергнуть и зависит от его логической формы .

Содержание

1 Аргументы
2 Действительная формула
3 Утверждения
4 Обоснованность
5 Удовлетворенность
6 Сохранение
7 См. Также
8 Ссылки
9 Дополнительная литература

Аргументы

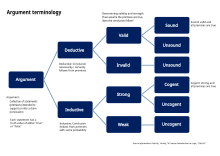Терминология аргументов, используемая в логике

В логике аргумент - это набор утверждений, выражающих предпосылки (все, что состоит из эмпирических свидетельств и аксиоматических истин) и вывод, основанный на свидетельствах.

Аргумент действителен тогда и только тогда, когда он противоречит тому, что вывод будет ложным, если все предпосылки верны. Валидность не требует истинности посылок, вместо этого она просто требует, чтобы вывод вытекал из форм, не нарушая правильности логической формы. Если также доказана истинность посылок действительного аргумента, это называется здравым.

соответствующее условное допустимого аргумента является логической истиной, а отрицание соответствующего ему условного выражения является противоречием. Заключение является логическим следствием его посылок.

Недействительный аргумент считается «недопустимым».

Пример действительного аргумента дает следующий хорошо известный силлогизм :

Все люди смертны.

Сократ - человек.

Следовательно, Сократ смертен.

Этот аргумент является достоверным не потому, что он имеет истинные посылки и истинный вывод, а из-за логической необходимости заключения, учитывая эти две посылки. Аргумент был бы столь же верным, если бы посылки и заключение были ложными. Следующий аргумент имеет ту же логическую форму, но с ложными предпосылками и ложным выводом, и он одинаково верен:

Все чашки зеленые.

Сократ - это чашка.

Следовательно, Сократ зеленый.

Независимо от того, как Вселенная могла быть построена, ни в коем случае не могло быть случая, чтобы эти аргументы имели одновременно истинные посылки, но ложное заключение. Приведенным выше аргументам можно противопоставить следующий неверный:

Все люди бессмертны.

Сократ - человек.

Следовательно, Сократ смертен.

В данном случае вывод противоречит дедуктивной логике предыдущих посылок, а не вытекает из нее. Следовательно, этот аргумент является логически «недействительным», даже если вывод можно считать «истинным» в общих чертах. Предпосылка «Все люди бессмертны» также была бы признана ложной вне рамок классической логики. Однако внутри этой системы «истина» и «ложь» по существу функционируют больше как математические состояния, такие как двоичные единицы и нули, чем как философские концепции, обычно связанные с этими терминами.

Стандартное представление состоит в том, что допустимость аргумента зависит от его логической формы . Логики используют множество техник для представления логической формы аргумента. Простой пример, примененный к двум из приведенных выше иллюстраций, следующий: пусть буквы «P», «Q» и «S» обозначают, соответственно, множество людей, множество смертных и Сократа. Используя эти символы, первый аргумент может быть сокращен как:

Все P - это Q.

S - это P.

Следовательно, S - это Q.

Аналогично, второй аргумент принимает следующий вид:

Все P не являются Q.

S является P.

Следовательно, S является Q.

Аргумент называется формально действительным, если он имеет структурную самосогласованность, то есть, если все операнды между предпосылками верны, полученный вывод всегда также верен. В третьем примере исходные посылки не могут логически привести к заключению и поэтому классифицируются как неверный аргумент.

Действительная формула

Формула формального языка является допустимой формулой тогда и только тогда, когда она верна при каждой возможной интерпретации языка. В логике высказываний это тавтологии.

Утверждения

Утверждение можно назвать действительным, то есть логической истиной, если оно истинно во всех интерпретациях.

Обоснованность

Действительность вывода не зависит от истинности посылки или истинности вывода. Следующий вывод совершенно верен:

Все животные живут на Марсе.

Все люди - животные.

Следовательно, все люди живут на Марсе.

Проблема с аргументом заключается в том, что что это не звук. Для того, чтобы дедуктивный аргумент был верным, аргумент должен быть верным и все предпосылки должны быть верными.

Выполнимость

Теория моделей анализирует формулы относительно определенных классов интерпретации в подходящей математической конструкции. При таком прочтении формула действительна, если все такие интерпретации подтверждают ее. Вывод действителен, если все интерпретации, подтверждающие предположения, подтверждают вывод. Это известно как семантическая достоверность.

Сохранение

При сохранении истины интерпретация, при которой всем переменным присваивается значение истинности «истина», дает истину значение «истина».

В действии с сохранением ложности интерпретация, при которой всем переменным присваивается значение истинности «ложь», дает значение истинности «ложь».

Свойства сохранения	Логическая связка предложения
Истинное и ложное сохранение:	Предложение • Логическая конъюнкция (И, $∧ {\ displaystyle \ land}$ $\ land$ ) • Логическая дизъюнкция (OR, $∨ {\ displaystyle \ lor}$ $\ lor$ )
Только истинное сохранение:	Тавтология ( $⊤ {\ displaystyle \ top}$ $\ top$ ) • Biconditional (XNOR, $↔ {\ displaystyle \ leftrightarrow}$ $\ leftrightarrow$ ) • Implication ( $→ {\ displaystyle \ rightarrow}$ $\ rightarrow$ ) • Обратное значение ( $← {\ displaystyle \ leftarrow}$ $\ leftarrow$ )
Только ложное сохранение:	Противоречие ( $⊥ {\ displaystyle \ bot}$ $\ bot$ ) • Исключительная дизъюнкция (XOR, $⊕ {\ displaystyle \ oplus}$ $\ oplus$ ) • Без импликации ( $↛ {\ displaystyle \ nrightarrow}$ $\ nrightarrow$ ) • Converse без импликации ( $↚ {\ displaystyle \ nleftarrow}$ $\ nleftarrow$ )
без сохранения) :	Отрицание ( $¬ {\ displaystyle \ neg}$ $\ neg$ ) • Альтернатива отрицание (NAND, $↑ {\ displaystyle \ uparrow}$ $\ uparrow$ ) • Совместное отрицание (NOR, $↓ {\ displaystyle \ downarrow}$ $\ downarrow$ )

См. также

Философский портал

Ссылки

Дополнительная литература

Барвайз, Джон ; Этчменди, Джон. Язык, доказательство и логика (1999): 42.
Бир, Фрэнсис А. «Достоверность: перспектива политической науки », Социальная эпистемология 7, 1 (1993): 85-105.