Квантовая система с двумя состояниями

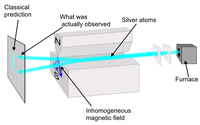
Пучок электрически нейтральных атомов серебра через неоднородное магнитное поле эксперимента Штерна-Герлаха разделяется на два, каждое из которых соответствует одному возможному значению спина самого дальнего электрона атома серебра.

В квантовой механике система с двумя состояниями (также известная как двухуровневая система) - это квантовая система, которая может существовать в любой квантовой суперпозиции двух независимых (физически различимых) квантовых состояний. Гильбертово пространство описания такой системы является двух- мерным. Следовательно, полный базис, охватывающий пространство, будет состоять из двух независимых состояний. Любую систему с двумя состояниями также можно рассматривать как кубит.

Системы с двумя состояниями - это простейшие квантовые системы, которые представляют интерес, поскольку динамика системы с одним состоянием тривиальна (поскольку нет других состояний, в которых система может существовать). Математическая основа, необходимая для анализа систем с двумя состояниями, - это линейные дифференциальные уравнения и линейная алгебра двумерных пространств. В результате динамика системы с двумя состояниями может быть решена аналитически без какого-либо приближения. Общее поведение системы состоит в том, что амплитуда волновой функции колеблется между двумя состояниями.

Очень хорошо известным примером двух состояний системы является спин из спин-1/2 частицы, такие как электрон, чей спин может иметь значения + ħ / 2 или - ħ / 2, где ħ является приведенная постоянная Планка.

Система с двумя состояниями не может использоваться для описания поглощения или распада, потому что такие процессы требуют связи с континуумом. Такие процессы будут включать экспоненциальное затухание амплитуд, но решения системы с двумя состояниями являются колебательными.

• 1 Аналитические решения для энергий стационарного состояния и зависимости от времени
  • 1.1 Представление
  • 1.2 Собственные значения гамильтониана
  • 1.3 Временная зависимость
  • 1.4 Формула Раби для статического возмущения
• 2 Некоторые важные системы с двумя состояниями
  • 2.1 Прецессия в поле
  • 2.2 Эволюция в поле, зависящем от времени: ядерный магнитный резонанс
  • 2.3 Связь с уравнениями Блоха
• 3 Срок действия
• 4 Значение и другие примеры
• 5 Дальнейшее чтение
• 6 См. Также
• 7 ссылки

Представление

Предположим, что двумя доступными базисными состояниями системы являются и, в общем, состояние можно записать как суперпозицию этих двух состояний с амплитудами вероятности, ${\ displaystyle | 1 \ rangle}$${\ displaystyle | 2 \ rangle}$ ${\ displaystyle c_ {1}, c_ {2}}$

${\ displaystyle | \ psi \ rangle = c_ {1} | 1 \ rangle + c_ {2} | 2 \ rangle.}$

Поскольку базисные состояния ортонормированы, где и - дельта Кронекера, поэтому. Эти два комплексных числа можно рассматривать как координаты в двумерном комплексном гильбертовом пространстве. Таким образом, вектор состояния, соответствующий состоянию, равен ${\ displaystyle \ langle i | j \ rangle = \ delta _ {ij}}$${\ displaystyle i, j \ in {1,2}}$${\ displaystyle \ delta _ {ij}}$ ${\ displaystyle c_ {i} = \ langle i | \ psi \ rangle}$ ${\ displaystyle | \ psi \ rangle}$

${\ displaystyle | \ psi \ rangle \ Equiv {\ begin {pmatrix} \ langle 1 | \ psi \ rangle \\\ langle 2 | \ psi \ rangle \ end {pmatrix}} = {\ begin {pmatrix} c_ {1 } \\ c_ {2} \ end {pmatrix}} = c_ {1} {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}} + c_ {2} {\ begin {pmatrix} 0 \\ 1 \ конец {pmatrix}} = \ mathbf {c},}$

а базисные состояния соответствуют базисным векторам, и. ${\ Displaystyle | 1 \ rangle \ Equiv {\ begin {pmatrix} \ langle 1 | 1 \ rangle \\\ langle 2 | 1 \ rangle \ end {pmatrix}} = {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}}}$${\ Displaystyle | 2 \ rangle \ Equiv {\ begin {pmatrix} \ langle 1 | 2 \ rangle \\\ langle 2 | 2 \ rangle \ end {pmatrix}} = {\ begin {pmatrix} 0 \\ 1 \ end {pmatrix}}}$

Если состояние будет нормализована, то норма о statevector равна единице, то есть. ${\ displaystyle | \ psi \ rangle}$ ${\ Displaystyle {| c_ {1} |} ^ {2} + {| c_ {2} |} ^ {2} = 1}$

Все наблюдаемые физические величины, такие как энергия, связаны с эрмитовыми операторами. В случае энергии и соответствующего гамильтонова, H, это означает,

${\ Displaystyle H_ {ij} = \ langle i | H | j \ rangle = \ langle j | H | i \ rangle ^ {*} = H_ {ji} ^ {*},}$

т.е. и реальны, и. Таким образом, эти четыре матричных элемента образуют эрмитову матрицу 2 × 2, ${\ displaystyle H_ {11}}$${\ displaystyle H_ {22}}$${\ displaystyle H_ {12} = H_ {21} ^ {*}}$${\ displaystyle H_ {ij}}$

${\ displaystyle \ mathbf {H} = {\ begin {pmatrix} \ langle 1 | H | 1 \ rangle amp; \ langle 1 | H | 2 \ rangle \\\ langle 2 | H | 1 \ rangle amp; \ langle 2 | H | 2 \ rangle \ end {pmatrix}} = {\ begin {pmatrix} H_ {11} amp; H_ {12} \\ H_ {12} ^ {*} amp; H_ {22} \ end {pmatrix}}.}$

Не зависящее от времени уравнение Шредингера утверждает, что ; замена на в терминах базисных состояний сверху и предварительное умножение обеих сторон на или дает систему двух линейных уравнений, которые могут быть записаны в матричной форме, ${\ Displaystyle H | \ psi \ rangle = E | \ psi \ rangle}$${\ displaystyle | \ psi \ rangle}$${\ displaystyle \ langle 1 |}$${\ displaystyle \ langle 2 |}$

${\ displaystyle {\ begin {pmatrix} H_ {11} amp; H_ {12} \\ H_ {12} ^ {*} amp; H_ {22} \ end {pmatrix}} {\ begin {pmatrix} c_ {1} \\ c_ {2} \ end {pmatrix}} = E {\ begin {pmatrix} c_ {1} \\ c_ {2} \ end {pmatrix}},}$

или которая является проблемой собственных значений матрицы 2 × 2 и собственных векторов. ${\ Displaystyle \ mathbf {Hc} = E \ mathbf {c}}$

Из-за скрытности собственные значения действительны; или, скорее, наоборот, это требование, чтобы энергии были реальными, что подразумевает отшельничность. Собственные векторы представляют собой стационарные состояния, т. Е. Такие, для которых абсолютная величина квадратов амплитуд вероятностей не меняется со временем. ${\ displaystyle \ mathbf {H}}$${\ displaystyle \ mathbf {H}}$

Собственные значения гамильтониана

Наиболее общий вид эрмитовой матрицы 2 × 2, такой как гамильтониан системы с двумя состояниями, имеет вид

${\ displaystyle \ mathbf {H} = {\ begin {pmatrix} \ epsilon _ {1} amp; \ beta -i \ gamma \\\ beta + i \ gamma amp; \ epsilon _ {2} \ end {pmatrix}}, }$

где и γ - действительные числа с единицами энергии. Разрешенные уровни энергии системы, а именно собственные значения матрицы гамильтониана, можно найти обычным способом. ${\ displaystyle \ epsilon _ {1}, \ epsilon _ {2}, \ beta}$

Эквивалентно эту матрицу можно разложить как,

${\ displaystyle \ mathbf {H} = \ alpha \ cdot \ sigma _ {0} + \ beta \ cdot \ sigma _ {1} + \ gamma \ cdot \ sigma _ {2} + \ delta \ cdot \ sigma _ { 3} = {\ begin {pmatrix} \ alpha + \ delta amp; \ beta -i \ gamma \\\ beta + i \ gamma amp; \ alpha - \ delta \ end {pmatrix}}.}$

Вот и настоящие числа. Матрица - это единичная матрица 2 × 2, а матрицы - это матрицы Паули. Это разложение упрощает анализ системы, особенно в случае, когда значения и являются постоянными. ${\ Displaystyle \ альфа = {\ гидроразрыва {(\ эпсилон _ {1} + \ эпсилон _ {2})} {2}}}$${\ displaystyle \ delta = {\ frac {(\ epsilon _ {1} - \ epsilon _ {2})} {2}}}$${\ displaystyle \ sigma _ {0}}$${\ displaystyle \ sigma _ {k}}$ ${\ Displaystyle (к = 1,2,3)}$ ${\ Displaystyle \ альфа, \ бета, \ гамма}$${\ displaystyle \ delta}$

Далее гамильтониан можно сжать как

${\ displaystyle \ mathbf {H} = \ alpha \ cdot \ sigma _ {0} + \ mathbf {r} \ cdot \ mathbf {\ sigma}.}$

Вектор задается как и задается как. Это представление упрощает анализ эволюции системы во времени и его легче использовать с другими специализированными представлениями, такими как сфера Блоха. ${\ displaystyle \ mathbf {r}}$${\ Displaystyle (\ бета, \ гамма, \ дельта)}$${\ displaystyle \ sigma}$${\ Displaystyle (\ sigma _ {1}, \ sigma _ {2}, \ sigma _ {3})}$

Если независимый от времени гамильтониан H системы с двумя состояниями определяется, как указано выше, то его собственные значения задаются выражением. Очевидно, что α средняя энергия двух уровней, а норма в это расщепление между ними. Соответствующие собственные векторы обозначены как и. ${\ Displaystyle E _ {\ pm} = \ альфа \ pm | \ mathbf {r} |}$ ${\ displaystyle \ mathbf {r}}$${\ displaystyle | + \ rangle}$${\ displaystyle | - \ rangle}$

Зависимость от времени

Теперь предположим, что амплитуды вероятностей зависят от времени, а базисные состояния - нет. Уравнение Шредингера, зависящее от времени, устанавливает и действует, как и раньше (замена и предварительное умножение на снова дает пару связанных линейных уравнений, но на этот раз они являются уравнениями в частных производных первого порядка:. Если не зависит от времени, существует несколько подходов к нахождению зависимость от времени, например нормальные режимы. В результате ${\ displaystyle i \ hbar {\ frac {\ partial} {\ partial t}} | \ psi \ rangle = H | \ psi \ rangle}$${\ displaystyle | \ psi \ rangle}$${\ Displaystyle \ langle 1 |, \ langle 2 |}$${\ displaystyle i \ hbar {\ frac {\ partial} {\ partial t}} \ mathbf {c} = \ mathbf {Hc}}$${\ displaystyle \ mathbf {H}}$${\ displaystyle c_ {1}, c_ {2}}$

${\ displaystyle \ mathbf {c} (t) = e ^ {- i \ mathbf {H} t / \ hbar} \ mathbf {c} _ {0} = \ mathbf {U} (t) \ mathbf {c} _ {0}.}$

где находится вектор состояний. Здесь экспоненту матрицы можно найти из разложения в ряд. Матрица называется матрицей временной эволюции (которая включает матричные элементы соответствующего оператора временной эволюции). Легко доказать, что он унитарен, а это значит, что. ${\ Displaystyle \ mathbf {c} _ {0} = \ mathbf {c} (0)}$${\ displaystyle t = 0}$ ${\ Displaystyle \ mathbf {U} (т)}$${\ Displaystyle U (т)}$${\ Displaystyle \ mathbf {U} (т)}$ ${\ Displaystyle \ mathbf {U} ^ {\ dagger} \ mathbf {U} = 1}$

Можно показать, что

${\ displaystyle \ mathbf {U} (t) = e ^ {- i \ mathbf {H} t / \ hbar} = e ^ {- i \ alpha t / \ hbar} (\ cos (| \ mathbf {r}) | t / \ hbar) \ sigma _ {0} -i \ sin (| \ mathbf {r} | t / \ hbar) {\ hat {r}} \ cdot \ mathbf {\ sigma}),}$

где ${\ displaystyle {\ hat {r}} = {\ frac {\ mathbf {r}} {| \ mathbf {r} |}}.}$

Когда один изменяет основу для собственных векторов гамильтониана, иными словами, если базисные состояния выбираются собственные векторы, то и поэтому гамильтониан диагоналей, то есть и формы, ${\ displaystyle | 1 \ rangle, | 2 \ rangle}$${\ displaystyle \ epsilon _ {1} = H_ {11} = \ langle 1 | H | 1 \ rangle = E_ {1} \ langle 1 | 1 \ rangle = E_ {1}}$${\ Displaystyle \ бета + я \ гамма = H_ {21} = \ langle 2 | H | 1 \ rangle = E_ {1} \ langle 2 | 1 \ rangle = 0}$${\ displaystyle | \ mathbf {r} | = \ delta}$

${\ displaystyle \ mathbf {H} = {\ begin {pmatrix} E_ {1} amp; 0 \\ 0 amp; E_ {2} \ end {pmatrix}}.}$

Теперь легко увидеть, что оператор унитарной временной эволюции задается следующим образом: ${\ displaystyle U}$

${\ displaystyle \ mathbf {U} (t) = e ^ {- i \ mathbf {H} t / \ hbar} = {\ begin {pmatrix} e ^ {- iE_ {1} t / \ hbar} amp; 0 \\ 0 amp; e ^ {- iE_ {2} t / \ hbar} \ end {pmatrix}} = e ^ {- i \ alpha t / \ hbar} {\ begin {pmatrix} e ^ {- i \ delta t / \ hbar} amp; 0 \\ 0 amp; e ^ {i \ delta t / \ hbar} \ end {pmatrix}} = e ^ {- i \ alpha t / \ hbar} (\ cos (\ delta t / \ hbar) \ sigma _ {0} -i \ sin (\ delta t / \ hbar) \ mathbf {\ sigma} _ {3}).}$

Фактор только способствует общей фазе оператора, и, как правило, можно пренебречь, чтобы получить новый временный оператор эволюции, который физически неотличим от исходного оператора. Более того, любое возмущение системы (которое будет иметь ту же форму, что и гамильтониан) может быть добавлено к системе в собственном базисе невозмущенного гамильтониана и проанализировано так же, как и выше. Следовательно, для любого возмущения новые собственные векторы возмущенной системы могут быть решены точно, как упомянуто во введении. ${\ Displaystyle е ^ {- я \ альфа т / \ hbar}}$

Формула Раби для статического возмущения

Предположим, что система начинается в одном из базовых состояний, скажем так, и нас интересует вероятность заполнения каждого из базовых состояний как функция времени, когда является независимым от времени гамильтонианом. ${\ displaystyle t = 0}$${\ displaystyle | 1 \ rangle}$${\ displaystyle \ mathbf {c} _ {0} = {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}}}$${\ displaystyle \ mathbf {H}}$

${\ displaystyle \ mathbf {c} (t) = \ mathbf {U} (t) \ mathbf {c} _ {0} = {\ begin {pmatrix} U_ {11} (t) amp; U_ {12} (t) \\ U_ {21} (t) amp; U_ {22} (t) \ end {pmatrix}} {\ begin {pmatrix} 1 \\ 0 \ end {pmatrix}} = {\ begin {pmatrix} U_ {11} ( t) \\ U_ {21} (t) \ end {pmatrix}}.}$

Вероятность оккупации государства i равна. В случае исходного состояния, и сверху,. Следовательно, ${\ Displaystyle P_ {i} (t) = | c_ {i} (t) | ^ {2} = | U_ {i1} (t) | ^ {2}}$${\ Displaystyle P_ {1} (t) = | c_ {1} (t) | ^ {2} = | U_ {11} (t) | ^ {2}}$${\ displaystyle U_ {11} (t) = e ^ {\ frac {-i \ alpha t} {\ hbar}} (\ cos (| \ mathbf {r} | t / \ hbar) -i \ sin (| \ mathbf {r} | t / \ hbar) {\ frac {\ delta} {| \ mathbf {r} |}})}$

${\ displaystyle P_ {1} (t) = \ cos ^ {2} (\ Omega t) + \ sin ^ {2} (\ Omega t) {\ frac {\ Delta ^ {2}} {\ Omega ^ { 2}}}.}$

Очевидно, из-за начального состояния. Частота называется обобщенной частотой Раби, называется частотой Раби и называется расстройкой. ${\ Displaystyle P_ {1} (0) = 1}$${\ displaystyle \ Omega = | \ mathbf {r} | / \ hbar = {\ sqrt {\ beta ^ {2} + \ gamma ^ {2} + \ delta ^ {2}}} / \ hbar = {\ sqrt {| \ Omega _ {R} | ^ {2} + \ Delta ^ {2}}}}$${\ Displaystyle \ Omega _ {R} = (\ бета + я \ гамма) / \ hbar}$${\ displaystyle \ Delta = \ delta / \ hbar}$

При нулевой расстройке, т. Е. Происходит переход Раби от гарантированного занятия состояния 1 к гарантированному заполнению состояния 2 и обратно в состояние 1 и т. Д. С частотой. По мере увеличения отстройки от нуля частота флопа увеличивается (до Ω), а амплитуда уменьшается до. ${\ Displaystyle P_ {1} (t) = \ cos ^ {2} (| \ Omega _ {R} | t)}$${\ displaystyle | \ Omega _ {R} |}$${\ Displaystyle 1- \ Delta ^ {2} / \ Omega ^ {2}}$

Для зависящих от времени гамильтонианов, индуцированных световыми волнами,

Смотрите также: цикл Раби и приближение вращающейся волны

Прецессия в поле

Рассмотрим случай частицы со спином 1/2 в магнитном поле. Гамильтониан взаимодействия для этой системы равен ${\ Displaystyle \ mathbf {B} = B \ mathbf {\ шляпа {п}}}$

${\ displaystyle H = - {\ boldsymbol {\ mu}} \ cdot \ mathbf {B} = - \ mu {\ boldsymbol {\ sigma}} \ cdot \ mathbf {B},}$

где это величина частицы магнитного момента и представляет собой вектор матриц Паули. Решение зависящего от времени уравнения Шредингера дает ${\ displaystyle \ mu}$ ${\ displaystyle {\ boldsymbol {\ sigma}}}$ ${\ Displaystyle H \ psi = я \ hbar \ partial _ {t} \ psi}$

${\ displaystyle \ psi (t) = e ^ {я \ omega t {\ boldsymbol {\ sigma}} \ cdot \ mathbf {\ hat {n}}} \ psi (0),}$

где и. Физически это соответствует прецессии вектора Блоха с угловой частотой. Без ограничения общности предположим, что поле однородно в точках, так что оператор временной эволюции задается как ${\ displaystyle \ omega = \ mu B / \ hbar}$${\ displaystyle e ^ {я \ omega t {\ boldsymbol {\ sigma}} \ cdot \ mathbf {\ hat {n}}} = \ cos {\ left (\ omega t \ right)} I + i \; \ mathbf {\ hat {n}} \ cdot {\ boldsymbol {\ sigma}} \ sin {\ left (\ omega t \ right)}}$ ${\ Displaystyle \ mathbf {\ шляпа {п}}}$${\ displaystyle 2 \ omega}$${\ displaystyle \ mathbf {\ hat {z}}}$

${\ displaystyle e ^ {я \ omega t {\ boldsymbol {\ sigma}} \ cdot \ mathbf {\ hat {n}}} = {\ begin {pmatrix} e ^ {i \ omega t} amp; 0 \\ 0 amp; e ^ {-i \ omega t} \ end {pmatrix}}.}$

Можно видеть, что такой оператор временной эволюции, действующий на общее состояние спина частицы со спином 1/2, приведет к прецессии вокруг оси, определяемой приложенным магнитным полем (это квантово-механический эквивалент ларморовской прецессии ).

Вышеупомянутый метод может быть применен к анализу любой типовой системы с двумя состояниями, которая взаимодействует с некоторым полем (эквивалентным магнитному полю в предыдущем случае), если взаимодействие задается подходящим членом связи, аналогичным магнитному моменту. Прецессию вектора состояния (которая не обязательно должна быть физическим вращением, как в предыдущем случае) можно рассматривать как прецессию вектора состояния на сфере Блоха.

Представление на сфере Блоха для вектора состояния будет просто вектором ожидаемых значений. В качестве примера рассмотрим вектор состояния, который является нормализованной суперпозицией и, то есть вектор, который может быть представлен в базисе как ${\ displaystyle \ psi (0)}$${\ displaystyle \ mathbf {R} = \ left (\ langle \ sigma _ {x} \ rangle, \ langle \ sigma _ {y} \ rangle, \ langle \ sigma _ {z} \ rangle \ right)}$${\ displaystyle \ psi (0)}$${\ Displaystyle \ влево | \ вверх \ вправо \ rangle}$${\ displaystyle \ left | \ downarrow \ right \ rangle}$${\ displaystyle \ sigma _ {z}}$

${\ displaystyle \ psi (0) = {\ frac {1} {\ sqrt {2}}} {\ begin {pmatrix} 1 \\ 1 \ end {pmatrix}}}$

Компоненты на сфере Блоха будут просто. Это единичный вектор, который начинает указывать и прецессирует в левом направлении. В общем, вращением вокруг любой вектор состояния может быть представлен как с действительными коэффициентами и. Такой вектор состояния соответствует вектору Блоха в плоскости xz, составляющему угол с осью z. Этот вектор продолжит прецессию вокруг. Теоретически, позволяя системе взаимодействовать с полем определенного направления и силы в течение определенных промежутков времени, можно получить любую ориентацию вектора Блоха, что эквивалентно получению любой сложной суперпозиции. Это основа для множества технологий, включая квантовые вычисления и МРТ. ${\ Displaystyle \ psi (т)}$${\ displaystyle \ mathbf {R} = \ left (\ cos {2 \ omega t}, - \ sin {2 \ omega t}, 0 \ right)}$${\ displaystyle \ mathbf {\ hat {x}}}$${\ displaystyle \ mathbf {\ hat {z}}}$${\ displaystyle \ mathbf {\ hat {z}}}$${\ displaystyle \ psi (0)}$${\ displaystyle a \ left | \ uparrow \ right \ rangle + b \ left | \ downarrow \ right \ rangle}$${\ displaystyle a}$${\ displaystyle b}$ ${\ Displaystyle \ загар (\ тета / 2) = б / а}$${\ displaystyle \ mathbf {\ hat {z}}}$

Эволюция в поле, зависящее от времени: ядерный магнитный резонанс

Ядерный магнитный резонанс (ЯМР) является важным примером динамики систем с двумя состояниями, поскольку он включает точное решение зависящего от времени гамильтониана. Явление ЯМР достигается помещением ядра в сильное статическое поле B 0 («удерживающее поле») и последующим приложением слабого поперечного поля B 1, которое колеблется на некоторой радиочастоте ω r. Явно рассмотрим частицу со спином 1/2 в удерживающем поле и поперечное высокочастотное поле B 1, вращающееся в плоскости xy вправо вокруг B 0: ${\ displaystyle B_ {0} \ mathbf {\ hat {z}}}$

${\ displaystyle \ mathbf {B} = {\ begin {pmatrix} B_ {1} \ cos \ omega _ {\ mathrm {r}} t \\ B_ {1} \ sin \ omega _ {\ mathrm {r}} t \\ B_ {0} \ end {pmatrix}}.}$

Как и в случае свободной прецессии, гамильтониан равен, а эволюция вектора состояния находится путем решения нестационарного уравнения Шредингера. После некоторых манипуляций (приведенных в свернутом разделе ниже) можно показать, что уравнение Шредингера принимает вид ${\ displaystyle H = - \ mu {\ boldsymbol {\ sigma}} \ cdot \ mathbf {B}}$${\ Displaystyle \ psi (т)}$${\ Displaystyle H \ psi = я \ hbar \, \ partial \ psi / \ partial t}$

${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = я \ left (\ omega _ {1} \ sigma _ {x} + \ left (w_ {0} + {\ frac {\ omega _ {r}} {2}} \ right) \ sigma _ {z} \ right) \ psi,}$

где и. ${\ displaystyle \ omega _ {0} = \ mu B_ {0} / \ hbar}$${\ displaystyle \ omega _ {1} = \ mu B_ {1} / \ hbar}$

Как и в предыдущем разделе, решение этого уравнения имеет прецессию вектора Блоха с частотой, в два раза превышающей величину вектора. Если он достаточно сильный, некоторая часть спинов будет направлена ​​прямо вниз до введения вращающегося поля. Если угловая частота вращающегося магнитного поля выбрана так, что во вращающейся системе координат вектор состояния будет прецессировать с частотой и, таким образом, будет переключаться с вниз на вверх, высвобождая энергию в виде детектируемых фотонов. Это фундаментальная основа ЯМР, и на практике это достигается сканированием до тех пор, пока не будет найдена резонансная частота, при которой образец будет излучать свет. Подобные расчеты проводятся в атомной физике, и в случае, когда поле не вращается, а колеблется с комплексной амплитудой, для получения таких результатов используется приближение вращающейся волны. ${\ displaystyle (\ omega _ {1}, 0, \ omega _ {0} + \ omega _ {r} / 2)}$${\ displaystyle \ omega _ {0}}$${\ displaystyle \ omega _ {r} = - 2 \ omega _ {0}}$${\ displaystyle {\ hat {x}}}$${\ displaystyle 2 \ omega _ {1}}$ ${\ displaystyle \ omega _ {r}}$

Вывод приведенного выше выражения для уравнения Шредингера ЯМР

Здесь уравнение Шредингера имеет вид ${\ displaystyle - \ mu {\ boldsymbol {\ sigma}} \ cdot \ mathbf {B} \ psi = i \ hbar {\ frac {\ partial \ psi} {\ partial t}}.}$ Расширение скалярного произведения и деление на урожайность ${\ displaystyle i \ hbar}$ ${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = я \ влево (\ omega _ {1} \ sigma _ {x} \ cos {\ omega _ {r} t} + \ omega _ {1} \ sigma _ {y} \ sin {\ omega _ {r} t} + \ omega _ {0} \ sigma _ {z} \ right) \ psi.}$ Чтобы исключить зависимость от времени из задачи, волновая функция преобразуется в соответствии с. Уравнение Шредингера, зависящее от времени, принимает вид ${\ displaystyle \ psi \ rightarrow e ^ {- я \ sigma _ {z} \ omega _ {r} t / 2} \ psi}$ ${\ displaystyle -i \ sigma _ {z} {\ frac {\ omega _ {r}} {2}} e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} \ psi + e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} {\ frac {\ partial \ psi} {\ partial t}} = i \ left (\ omega _ {1} \ sigma _ {x} \ cos {\ omega _ {r} t} + \ omega _ {1} \ sigma _ {y} \ sin {\ omega _ {r} t} + \ omega _ {0} \ sigma _ {z } \ right) e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} \ psi,}$ который после некоторой перестановки дает ${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = т.е. ^ {я \ sigma _ {z} \ omega _ {r} t / 2} \ left (\ omega _ {1} \ sigma _ {x} \ cos {\ omega _ {r} t} + \ omega _ {1} \ sigma _ {y} \ sin {\ omega _ {r} t} + \ left (\ omega _ {0} + {\ frac {\ omega _ {r}} {2}} \ right) \ sigma _ {z} \ right) e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} \ psi }$ Оценивая каждый член в правой части уравнения ${\ displaystyle e ^ {я \ sigma _ {z} \ omega _ {r} t / 2} \ sigma _ {x} e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} = {\ begin {pmatrix} e ^ {i \ omega _ {r} t / 2} amp; 0 \\ 0 amp; e ^ {- i \ omega _ {r} t / 2} \ end {pmatrix}} {\ begin {pmatrix } 0 amp; 1 \\ 1 amp; 0 \ end {pmatrix}} {\ begin {pmatrix} e ^ {- i \ omega _ {r} t / 2} amp; 0 \\ 0 amp; e ^ {i \ omega _ {r} t / 2} \ конец {pmatrix}} = {\ begin {pmatrix} 0 amp; e ^ {i \ omega _ {r} t} \\ e ^ {- i \ omega _ {r} t} amp; 0 \ end {pmatrix}}}$ ${\ displaystyle e ^ {я \ sigma _ {z} \ omega _ {r} t / 2} \ sigma _ {y} e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} = {\ begin {pmatrix} e ^ {i \ omega _ {r} t / 2} amp; 0 \\ 0 amp; e ^ {- i \ omega _ {r} t / 2} \ end {pmatrix}} {\ begin {pmatrix } 0 amp; -i \\ i amp; 0 \ end {pmatrix}} {\ begin {pmatrix} e ^ {- i \ omega _ {r} t / 2} amp; 0 \\ 0 amp; e ^ {i \ omega _ {r} t / 2 } \ end {pmatrix}} = {\ begin {pmatrix} 0 amp; -ie ^ {i \ omega _ {r} t} \\ ie ^ {- i \ omega _ {r} t} amp; 0 \ end {pmatrix}} }$ ${\ displaystyle e ^ {я \ sigma _ {z} \ omega _ {r} t / 2} \ sigma _ {z} e ^ {- i \ sigma _ {z} \ omega _ {r} t / 2} = {\ begin {pmatrix} e ^ {i \ omega _ {r} t / 2} amp; 0 \\ 0 amp; e ^ {- i \ omega _ {r} t / 2} \ end {pmatrix}} {\ begin {pmatrix } 1 amp; 0 \\ 0 amp; -1 \ end {pmatrix}} {\ begin {pmatrix} e ^ {- i \ omega _ {r} t / 2} amp; 0 \\ 0 amp; e ^ {i \ omega _ {r} t / 2 } \ end {pmatrix}} = \ sigma _ {z}}$ Теперь уравнение выглядит следующим образом: ${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = i \ left (\ omega _ {1} {\ begin {pmatrix} 0 amp; e ^ {i \ omega _ {r} t} \ left ( \ cos {\ omega _ {r} t} -i \ sin {\ omega _ {r} t} \ right) \\ e ^ {- i \ omega _ {r} t} \ left (\ cos {\ omega _ {r} t} + i \ sin {\ omega _ {r} t} \ right) amp; 0 \ end {pmatrix}} + \ left (w_ {0} + {\ frac {\ omega _ {r}} { 2}} \ right) \ sigma _ {z} \ right) \ psi,}$ который по тождеству Эйлера становится ${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = я \ left (\ omega _ {1} \ sigma _ {x} + \ left (w_ {0} + {\ frac {\ omega _ {r}} {2}} \ right) \ sigma _ {z} \ right) \ psi}$

Связь с уравнениями Блоха

Эти оптические уравнения Блоха для сбора спина-1/2 частиц могут быть получены из уравнения времени зависит Шредингер для системы из двух уровней. Исходя из ранее сформулированного гамильтониана, его можно записать в суммирующих обозначениях после некоторой перестановки как ${\ displaystyle i \ hbar \ partial _ {t} \ psi = - \ mu {\ vec {\ sigma}} \ cdot {\ vec {B}} \ psi}$

${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = i {\ frac {\ mu} {\ hbar}} \ sigma _ {i} B_ {i} \ psi}$

Умножение на матрицу Паули и сопряженное транспонирование волновой функции с последующим разложением произведения двух матриц Паули дает ${\ displaystyle \ sigma _ {я}}$

${\ displaystyle \ psi ^ {\ dagger} \ sigma _ {j} {\ frac {\ partial \ psi} {\ partial t}} = i {\ frac {\ mu} {\ hbar}} \ psi ^ {\ dagger} \ sigma _ {j} \ sigma _ {i} B_ {i} \ psi = i {\ frac {\ mu} {\ hbar}} \ psi ^ {\ dagger} \ left (I \ delta _ {ij } -i \ sigma _ {k} \ varepsilon _ {ijk} \ right) B_ {i} \ psi = {\ frac {\ mu} {\ hbar}} \ psi ^ {\ dagger} \ left (iI \ delta _ {ij} + \ sigma _ {k} \ varepsilon _ {ijk} \ right) B_ {i} \ psi}$

Добавление этого уравнения к его собственному сопряженному транспонированию дает левую часть формы

${\ displaystyle \ psi ^ {\ dagger} \ sigma _ {j} {\ frac {\ partial \ psi} {\ partial t}} + {\ frac {\ partial \ psi ^ {\ dagger}} {\ partial t }} \ sigma _ {j} \ psi = {\ frac {\ partial \ left (\ psi ^ {\ dagger} \ sigma _ {j} \ psi \ right)} {\ partial t}}}$

И правая часть формы

${\ displaystyle {\ frac {\ mu} {\ hbar}} \ psi ^ {\ dagger} \ left (iI \ delta _ {ij} + \ sigma _ {k} \ varepsilon _ {ijk} \ right) B_ { i} \ psi + {\ frac {\ mu} {\ hbar}} \ psi ^ {\ dagger} \ left (-iI \ delta _ {ij} + \ sigma _ {k} \ varepsilon _ {ijk} \ right) B_ {i} \ psi = {\ frac {2 \ mu} {\ hbar}} \ left (\ psi ^ {\ dagger} \ sigma _ {k} \ psi \ right) B_ {i} \ varepsilon _ { ijk}}$

Как упоминалось выше, среднее значение каждой матрицы Паули является компонентом вектора Блоха,. Приравнивая левую и правую части и учитывая, что это гиромагнитное отношение, получаем другую форму для уравнений движения вектора Блоха ${\ displaystyle \ langle \ sigma _ {i} \ rangle = \ psi ^ {\ dagger} \ sigma _ {i} \ psi = R_ {i}}$${\ displaystyle {\ frac {2 \ mu} {\ hbar}}}$ ${\ displaystyle \ gamma}$

${\ displaystyle {\ frac {\ partial R_ {j}} {\ partial t}} = \ gamma R_ {k} B_ {i} \ varepsilon _ {kij}}$

где то что было использовано. В векторной форме эти три уравнения могут быть выражены через перекрестное произведение ${\ Displaystyle \ varepsilon _ {ijk} = \ varepsilon _ {kij}}$

${\ displaystyle {\ frac {\ partial {\ vec {R}}} {\ partial t}} = \ gamma {\ vec {R}} \ times {\ vec {B}}}$

Классически это уравнение описывает динамику спина в магнитном поле. Идеальный магнит состоит из набора идентичных спинов, ведущих себя независимо, и, таким образом, общая намагниченность пропорциональна вектору Блоха. Все, что осталось для получения окончательной формы оптических уравнений Блоха, - это учет феноменологических релаксационных членов. ${\ displaystyle {\ vec {M}}}$ ${\ displaystyle {\ vec {R}}}$

В заключение, приведенное выше уравнение может быть получено путем рассмотрения временной эволюции оператора углового момента в картине Гейзенберга.

${\ displaystyle i \ hbar {\ frac {d \ sigma _ {j}} {dt}} = [\ sigma _ {j}, H] = [\ sigma _ {j}, - \ mu \ sigma _ {i } B_ {i}] = - \ mu \ left (\ sigma _ {j} \ sigma _ {i} B_ {i} - \ sigma _ {i} \ sigma _ {j} B_ {i} \ right) = \ mu [\ sigma _ {i}, \ sigma _ {j}] B_ {i} = 2 \ mu i \ varepsilon _ {ijk} \ sigma _ {k} B_ {i}}$

В сочетании с тем, что это уравнение является тем же уравнением, что и раньше. ${\ displaystyle {\ vec {R_ {i}}} = \ langle \ sigma _ {i} \ rangle}$

Системы с двумя состояниями - это простейшие нетривиальные квантовые системы, встречающиеся в природе, но вышеупомянутые методы анализа применимы не только для простых систем с двумя состояниями. Любую общую квантовую систему с несколькими состояниями можно рассматривать как систему с двумя состояниями, если наблюдаемая система имеет два собственных значения. Например, частица со спином 1/2 в действительности может иметь дополнительные поступательные или даже вращательные степени свободы, но эти степени свободы не имеют отношения к предыдущему анализу. Математически неучтенные степени свободы соответствуют вырождению собственных значений спина.

Другой случай, когда применим эффективный формализм двух состояний, - это когда рассматриваемая система имеет два уровня, которые эффективно отделены от системы. Так обстоит дело при анализе спонтанного или вынужденного излучения света атомами и зарядовых кубитов. В этом случае следует иметь в виду, что возмущения (взаимодействия с внешним полем) находятся в нужном диапазоне и не вызывают переходов в состояния, отличные от тех, которые представляют интерес.

С педагогической точки зрения формализм двух состояний является одним из простейших математических методов, используемых для анализа квантовых систем. Его можно использовать для иллюстрации фундаментальных квантово-механических явлений, таких как интерференция, проявляемая частицами состояний поляризации фотона, а также более сложных явлений, таких как осцилляция нейтрино или осцилляция нейтрального K-мезона.

Формализм двух состояний может использоваться для описания простого смешивания состояний, которое приводит к таким явлениям, как стабилизация резонанса и другие симметрии, связанные с пересечением уровней. Подобные явления находят широкое применение в химии. Явления с огромными промышленными применениями, такими как мазеры и лазеры, можно объяснить с помощью формализма двух состояний.

Формализм двух состояний также составляет основу квантовых вычислений. Кубиты, которые являются строительными блоками квантового компьютера, представляют собой не что иное, как системы с двумя состояниями. Любая квантовая вычислительная операция - это унитарная операция, которая вращает вектор состояния на сфере Блоха.

• Прекрасное описание формализма двух состояний и его применение почти ко всем приложениям, упомянутым в этой статье, представлено в третьем томе Лекций Фейнмана по физике.
• Следующий набор лекций охватывает необходимую математику, а также более подробно рассматривает несколько примеров:
  • из курса квантовой механики II, предлагаемого в Массачусетском технологическом институте, http://web.mit.edu/8.05/handouts/Twostates_03.pdf
  • из того же курса, посвященного колебаниям нейтральных частиц, http://web.mit.edu/8.05/handouts/nukaon_07.pdf
  • из курса квантовой механики I, предлагаемого в TIFR, http://theory.tifr.res.in/~sgupta/courses/qm2013/hand4.pdf охватывает основы математики
  • http://theory.tifr.res.in/~sgupta/courses/qm2013/hand5.pdf  ; из того же курса рассматриваются некоторые физические системы с двумя состояниями и другие важные аспекты формализма.
  • математика в начальном разделе выполняется аналогично этим заметкам http://www.math.columbia.edu/~woit/QM/qubit.pdf, которые взяты из курса « Квантовая механика для математиков», предлагаемого в Колумбийском университете..
  • книжная версия того же; http://www.math.columbia.edu/~woit/QM/qmbook.pdf
  • Системы с двумя состояниями и сфера, RJ Plymen, Il Nuovo Cimento B 13 (1973) 55-58

• Цикл Раби
• Дублет
• Ядерный магнитный резонанс
• Квантовая оптика