Топологическая сортировка

редактировать

В информатике используется топологическая сортировка или топологический порядок ориентированного графа - это линейный порядок его вершин, такой, что для каждого направленного ребра uv от вершины u до вершины v u стоит перед v в заказ. Например, вершины графа могут представлять задачи, которые должны быть выполнены, а ребра могут представлять ограничения, согласно которым одна задача должна быть выполнена раньше другой; в этом приложении топологический порядок - это просто допустимая последовательность для задач. Топологическое упорядочение возможно тогда и только тогда, когда граф не имеет направленных циклов, то есть если это ориентированный ациклический граф (DAG). Любой DAG имеет по крайней мере одно топологическое упорядочение, и известны алгоритмы для построения топологического упорядочения любого DAG за линейное время. Топологическая сортировка имеет множество приложений, особенно в задачах ранжирования, таких как набор дуг обратной связи.

Содержание

1 Примеры
2 Алгоритмы
- 2.1 Алгоритм Кана
- 2.2 Поиск в глубину
- 2.3 Параллельный алгоритмы
3 Применение для поиска кратчайшего пути
4 Уникальность
5 Отношение к частичным порядкам
6 См. также
7 Примечания
8 Ссылки
9 Дополнительная литература
10 Внешние ссылки

Примеры

Каноническое применение топологической сортировки - это планирование последовательности заданий или задач на основе их зависимостей. Задания представлены вершинами, и есть ребро от x до y, если задание x должно быть завершено до начала задания y (например, при стирке одежды стиральная машина должна закончить, прежде чем мы поместим одежду в сушилку). Затем топологическая сортировка задает порядок выполнения работ. Тесно родственное применение алгоритмов топологической сортировки было впервые изучено в начале 1960-х годов в контексте метода PERT для планирования в управлении проектами. В этом приложении вершины графа представляют вехи проекта, а ребра представляют задачи, которые необходимо выполнить между одним этапом и другим. Топологическая сортировка формирует основу алгоритмов линейного времени для поиска критического пути проекта, последовательности этапов и задач, которые контролируют продолжительность общего расписания проекта.

В информатике приложения этого типа возникают в планировании инструкций, упорядочивании вычисления ячеек формулы при пересчете значений формулы в электронных таблицах, логическом синтезе, определение порядка выполнения задач компиляции в make-файлах, сериализация данных и разрешение символьных зависимостей в компоновщиках. Он также используется, чтобы решить, в каком порядке загружать таблицы с внешними ключами в базы данных.

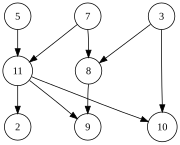График, показанный слева, имеет много допустимых топологических типов, включая:

5, 7, 3, 11, 8, 2, 9, 10 (визуально сверху вниз, слева направо). справа)
3, 5, 7, 8, 11, 2, 9, 10 (первая имеющаяся вершина с наименьшим номером)
5, 7, 3, 8, 11, 10, 9, 2 (сначала наименьшее количество ребер)
7, 5, 11, 3, 10, 8, 9, 2 (первая доступная вершина с наибольшим номером)
5, 7, 11, 2, 3, 8, 9, 10 (попытки сверху вниз, слева направо)
3, 7, 8, 5, 11, 10, 2, 9 (произвольно)

Алгоритмы

Обычные алгоритмы топологической сортировки имеют время работы, линейное по количеству узлов плюс количество ребер, асимптотически $O (| V | + | E |). {\ displaystyle O (\ left | {V} \ right | + \ left | {E} \ right |).}$ ${\ displaystyle O (\ left | {V} \ right | + \ left | {E} \ right |).}$

Алгоритм Кана

Один из этих алгоритмов, впервые описанный Каном (1962), работает, выбирая вершины в том же порядке, что и конечная топологическая сортировка. Сначала найдите список «начальных узлов», у которых нет входящих ребер, и вставьте их в набор S; хотя бы один такой узел должен существовать в непустом ациклическом графе. Затем:

L ← Пустой список, который будет содержать отсортированные элементы S ← Набор всех узлов без входящего ребра, в то время как S не пусто do удалить узел n из S добавить n к L для каждого узла m с ребром e от n до m do удалить ребро e из графа, если m не имеет других входящих ребер, затем вставьте m в S, если граф имеет ребра, затемверните ошибку (граф имеет хотя бы один цикл) elsereturn L (топологически отсортированный порядок)

Если график является DAG, решение будет содержаться в списке L ( решение не обязательно уникальное). В противном случае в графе должен быть хотя бы один цикл, поэтому топологическая сортировка невозможна.

Отражая неединственность результирующей сортировки, структура S может быть просто набором, очередью или стеком. В зависимости от порядка удаления узлов n из набора S создается другое решение. Вариант алгоритма Кана, который разрывает связи лексикографически, образует ключевой компонент алгоритма Коффмана – Грэма для параллельного планирования и рисования многоуровневого графа.

Поиск в глубину

Альтернативный алгоритм топологической сортировки основан на поиске в глубину. Алгоритм проходит через каждый узел графа в произвольном порядке, инициируя поиск в глубину, который завершается, когда он попадает в любой узел, который уже был посещен с начала топологической сортировки или у узла нет исходящих ребер (т. Е. листовой узел):

L ← Пустой список, который будет содержать отсортированные узлы, в то время как существуют узлы без постоянной метки do выбрать немаркированный узел n посещение (n) функция визит (узел n) если n имеет постоянную метку, тогдаreturn ifn имеет временную метку, затем stop (не DAG) отметка n с временной отметкой для каждого узла m с ребром от n до m do visit (m) удалить временную отметку из n отметить n постоянной меткой добавить n в начало L

Каждый узел n добавляется к выходному списку L только после рассмотрения всех других узлов, которые зависят от n (всех потомков n в графе). В частности, когда алгоритм добавляет узел n, мы гарантируем, что все узлы, зависящие от n, уже находятся в выходном списке L: они были добавлены в L либо рекурсивным вызовом visit (), который завершился перед вызовом visit n, или вызовом visit (), который начался еще до вызова visit n. Поскольку каждое ребро и узел посещаются один раз, алгоритм работает за линейное время. Этот алгоритм, основанный на поиске в глубину, описан Cormen et al. (2001) ; кажется, что он был впервые описан в печати Tarjan (1976).

Параллельные алгоритмы

На параллельной машине с произвольным доступом топологическое упорядочение может быть построено за O (log n) время с использованием полиномиального числа процессоров, помещая задачу в класс сложности NC. Один из способов сделать это - многократно возводить в квадрат матрицу смежности данного графа, логарифмически много раз, используя умножение матрицы мин-плюс с максимизацией вместо минимизации. Результирующая матрица описывает самый длинный путь расстояний на графике. Сортировка вершин по длинам их самых длинных входящих путей приводит к топологическому упорядочиванию.

Алгоритм параллельной топологической сортировки на машинах с распределенной памятью распараллеливает алгоритм Кана для DAG $G = (V, E) {\ displaystyle G = (V, E)}$ $G = ( V, E)$ . На высоком уровне алгоритм Кана многократно удаляет вершины степени 0 и добавляет их к топологической сортировке в том порядке, в котором они были удалены. Поскольку исходящие ребра удаленных вершин также удаляются, будет новый набор вершин степени 0, в котором процедура повторяется до тех пор, пока не останется ни одной вершины. Этот алгоритм выполняет $D + 1 {\ displaystyle D + 1}$ ${\ displaystyle D + 1}$ итераций, где D - самый длинный путь в G. Каждую итерацию можно распараллелить, что является идеей следующего алгоритма.

Далее предполагается, что раздел графа хранится на p обрабатывающих элементах (PE), которые помечены $0,…, p - 1 {\ displaystyle 0, \ dots, p-1}$ ${\ displaystyle 0, \ dots, p-1}$ . Каждый PE i инициализирует набор локальных вершин $Q i 1 {\ displaystyle Q_ {i} ^ {1}}$ ${\ displaystyle Q_ {i} ^ {1}}$ с степенью 0, где верхний индекс представляет текущий итерация. Поскольку все вершины в локальных множествах $Q 0 1,…, Q p - 1 1 {\ displaystyle Q_ {0} ^ {1}, \ dots, Q_ {p-1} ^ {1}}$ ${\ displaystyle Q_ {0} ^ {1}, \ точки, Q_ {p-1} ^ {1}}$ имеют степень 0, т. Е. Они не являются смежными, они могут быть указаны в произвольном порядке для правильной топологической сортировки. Чтобы присвоить глобальный индекс каждой вершине, сумма префикса вычисляется по размерам $Q 0 1,…, Q p - 1 1 {\ displaystyle Q_ {0} ^ {1}, \ точки, Q_ {p-1} ^ {1}}$ ${\ displaystyle Q_ {0} ^ {1}, \ точки, Q_ {p-1} ^ {1}}$ . Итак, на каждом шаге существует $∑ i = 0 p - 1 | Q i | В топологическую сортировку добавлены вершины {\ displaystyle \ sum _ {i = 0} ^ {p-1} | Q_ {i} |}$ ${\ displaystyle \ sum _ {i = 0} ^ {p-1} | Q_ {i} |}$ .

Выполнение параллельного алгоритма топологической сортировки на DAG с двумя элементами обработки.

На первом этапе PE j присваивает индексы $∑ i = 0 j - 1 | Q i 1 |,…, (∑ я знак равно 0 J | Q я 1 |) - 1 {\ displaystyle \ sum _ {я = 0} ^ {j-1} | Q_ {i} ^ {1} |, \ точки, \ влево (\ sum _ {i = 0} ^ {j} | Q_ {i} ^ {1} | \ right) -1}$ ${\ displaystyle \ sum _ {i = 0} ^ {j-1} | Q_ {i} ^ {1} |, \ dots, \ left (\ sum _ {i = 0} ^ {j} | Q_ { я} ^ {1} | \ right) -1}$ к локальным вершинам в $Q j 1 {\ displaystyle Q_ {j} ^ {1}}$ ${\ displaystyle Q_ {j} ^ {1}}$ . Эти вершины в $Q j 1 {\ displaystyle Q_ {j} ^ {1}}$ ${\ displaystyle Q_ {j} ^ {1}}$ удаляются вместе с соответствующими им исходящими ребрами. Для каждого исходящего ребра $(u, v) {\ displaystyle (u, v)}$ $(u, v)$ с конечной точкой v в другом PE $l, j ≠ l {\ displaystyle l, j \ neq l }$ ${\ displaystyle l, j \ neq l}$ , сообщение $(u, v) {\ displaystyle (u, v)}$ $(u, v)$ отправляется в PE l. После удаления всех вершин в $Q j 1 {\ displaystyle Q_ {j} ^ {1}}$ ${\ displaystyle Q_ {j} ^ {1}}$ опубликованные сообщения отправляются в соответствующий PE. Каждое полученное сообщение $(u, v) {\ displaystyle (u, v)}$ $(u, v)$ обновляет степень локальной вершины v. Если степень падает до нуля, v добавляется к $Q j 2 {\ displaystyle Q_ {j} ^ {2}}$ ${\ displaystyle Q_ {j} ^ {2}}$ . Затем начинается следующая итерация.

На этапе k PE j присваивает индексы $a k - 1 + ∑ i = 0 j - 1 | Q i k |,…, Ak - 1 + (∑ я = 0 j | Q ik |) - 1 {\ displaystyle a_ {k-1} + \ sum _ {i = 0} ^ {j-1} | Q_ {i} ^ {k} |, \ dots, a_ {k-1} + \ left (\ sum _ {i = 0} ^ {j} | Q_ {i} ^ {k} | \ right) -1}$ ${\ displaystyle a_ {k-1} + \ sum _ {i = 0} ^ {j-1} | Q_ {i} ^ {k} |, \ dots, a_ {k-1} + \ left (\ sum _ {i = 0} ^ {j} | Q_ {i} ^ {k} | \ right) -1}$ , где $ak - 1 {\ displaystyle a_ {k-1}}$ $a _ {{k-1}}$ - общее количество обработанных вершин после шага $k - 1 {\ displaystyle k-1}$ $k-1$ . Эта процедура повторяется до тех пор, пока не останется обработанных вершин, поэтому $∑ i = 0 p - 1 | Q i D + 1 | Знак равно 0 {\ displaystyle \ sum _ {i = 0} ^ {p-1} | Q_ {i} ^ {D + 1} | = 0}$ ${\ displaystyle \ sum _ {i = 0} ^ {p-1} | Q_ { i} ^ {D + 1} | = 0}$ . Ниже приведен общий обзор этого алгоритма, единственная программа, несколько данных псевдокода.

Обратите внимание, что префикс sum для локальных смещений $a k - 1 + ∑ i = 0 j - 1 | Q i k |,…, Ak - 1 + (∑ я = 0 j | Q ik |) - 1 {\ displaystyle a_ {k-1} + \ sum _ {i = 0} ^ {j-1} | Q_ {i} ^ {k} |, \ dots, a_ {k-1} + \ left (\ sum _ {i = 0} ^ {j} | Q_ {i} ^ {k} | \ right) -1}$ ${\ displaystyle a_ {k-1} + \ sum _ {i = 0} ^ {j-1} | Q_ {i} ^ {k} |, \ dots, a_ {k-1} + \ left (\ sum _ {i = 0} ^ {j} | Q_ {i} ^ {k} | \ right) -1}$ можно эффективно рассчитывать параллельно.

pэлементы обработки с идентификаторами от 0 до p-1 Input: $G = (V, E) {\ displaystyle G = (V, E)}$  $G = ( V, E)$ DAG, распределен между PE, индекс PE  $j ∈ {0,…, p - 1} {\ displaystyle j \ in \ {0, \ dots, p-1 \}}$  ${\ displaystyle j \ in \ {0, \ dots, p-1 \}}$ Вывод: топологическая сортировка G

функция traverseDAG Распределенная δ входящая степень локальных вершин VQ = {v ∈ V | δ [v] = 0} // Все вершины с степенью 0 nrOfVerticesProcessed = 0 doglobal строим сумму префикса по размеру Q // получаем смещения и общее количество вершин в этот шаг смещение = nrOfVerticesProcessed +  $∑ i = 0 j - 1 | Q i | {\ displaystyle \ sum _ {i = 0} ^ {j-1} | Q_ {i} |}$  ${\ displaystyle \ sum _ {i = 0} ^ {j-1} | Q_ {i} |}$ // j - индекс процессора foreach u ∈ Q localOrder [u ] = index ++; foreach (u, v) ∈ E do отправить сообщение (u, v) PE, владеющему вершиной v nrOfVerticesProcessed + =  $∑ i = 0 p - 1 | Q i | {\ displaystyle \ sum _ {i = 0} ^ {p-1} | Q_ {i} |}$  ${\ displaystyle \ sum _ {i = 0} ^ {p-1} | Q_ {i} |}$ доставить все сообщения соседям вершин в Q получить сообщения для локальных вершин V удалить все вершины в Q foreach получено сообщение (u, v): если --δ [v] = 0, добавить v к Q, а глобальный размер Q>0 return localOrder

Стоимость связи сильно зависит от данного раздела графа. Что касается времени выполнения, то в модели CRCW-PRAM, которая допускает выборку и декремент за постоянное время, этот алгоритм работает в $O (m + np + D (Δ + log ⁡ n)) { \ displaystyle {\ mathcal {O}} \ left ({\ frac {m + n} {p}} + D (\ Delta + \ log n) \ right)}$ ${\ displaystyle {\ mathcal {O}} \ left ({\ гидроразрыв {m + n} {p}} + D (\ Delta + \ log n) \ right)}$ , где D - снова самый длинный путь в G и Δ максимальная степень.

Приложение для поиска кратчайшего пути

Топологическое упорядочение также может использоваться для быстрого вычисления кратчайших путей через взвешенный ориентированный ациклический граф. Пусть V - список вершин такого графа в топологическом порядке. Затем следующий алгоритм вычисляет кратчайший путь от некоторой исходной вершины s ко всем остальным вершинам:

Пусть d будет массивом той же длины, что и V; это будет содержать кратчайшие расстояния от s. Установите d [s] = 0, все остальные d [u] = ∞.
Пусть p будет массивом той же длины, что и V, со всеми элементами, инициализированными равными нулю. Каждый p [u] будет содержать предшественника u на кратчайшем пути от s до u.
Цикл по вершинам u, как упорядочено в V, начиная с s:
- Для каждой вершины v непосредственно следующее за u (т.е. существует ребро от u до v):
  - Пусть w - вес ребра от u до v.
  - Ослабьте ребро: if d [v]>d [u] + w, положим
    - d [v] ← d [u] + w,
    - p [v] ← u.

На графе из n вершин и m ребер, этот алгоритм занимает Θ (n + m), т. е. линейное, время.

Уникальность

Если топологическая сортировка обладает тем свойством, что все пары последовательных вершины в отсортированном порядке соединяются ребрами, затем эти ребра образуют направленный гамильтонов путь в DAG. Если гамильтонов путь существует, топологический порядок сортировки уникален; никакой другой порядок не учитывает края пути. И наоборот, если топологическая сортировка не образует гамильтонов путь, DAG будет иметь два или более допустимых топологического порядка, поскольку в этом случае всегда можно сформировать второй допустимый порядок, поменяв местами две последовательные вершины, которые не соединены ребром. друг другу. Следовательно, можно проверить за линейное время, существует ли уникальный порядок и существует ли гамильтонов путь, несмотря на NP-трудность проблемы гамильтонова пути для более общих ориентированных графов.

Отношение к частичным порядкам

Топологические порядки также тесно связаны с концепцией линейного расширения частичного порядка в математике. В терминах высокого уровня существует присоединение между ориентированными графами и частичными порядками.

Частично упорядоченный набор - это просто набор объектов вместе с определением отношения неравенства «≤», удовлетворяющие аксиомам рефлексивности (x ≤ x), антисимметрии (если x ≤ y и y ≤ x, то x = y) и транзитивности (если x ≤ y и y ≤ z, то x ≤ z). Общий порядок - это частичный порядок, в котором для каждых двух объектов x и y в наборе либо x ≤ y, либо y ≤ x. Общие заказы известны в информатике как операторы сравнения, необходимые для выполнения алгоритмов сортировки сравнения. Для конечных наборов общие порядки могут быть идентифицированы с линейными последовательностями объектов, где отношение «≤» истинно всякий раз, когда первый объект предшествует второму объекту в порядке; для преобразования общего порядка в последовательность таким образом может использоваться алгоритм сортировки сравнения. Линейное расширение частичного порядка - это общий порядок, совместимый с ним, в том смысле, что если x ≤ y в частичном порядке, то x ≤ y также и в полном порядке.

Можно определить частичный порядок из любого DAG, позволив набору объектов быть вершинами DAG и определив x ≤ y как истинное для любых двух вершин x и y, если существует направленный путь от x до y; то есть всякий раз, когда y достижим из x. С этими определениями топологический порядок DAG - это то же самое, что и линейное расширение этого частичного порядка. И наоборот, любой частичный порядок на конечном множестве можно определить как отношение достижимости в DAG. Один из способов сделать это - определить группу DAG, которая имеет вершину для каждого объекта в частично упорядоченном наборе и ребро xy для каждой пары объектов, для которых x ≤ y. Альтернативный способ сделать это - использовать транзитивную редукцию частичного упорядочения; как правило, это создает группы DAG с меньшим количеством ребер, но отношение достижимости в этих группах DAG остается тем же частичным порядком. Используя эти конструкции, можно использовать алгоритмы топологического упорядочения для поиска линейных расширений частичных порядков.

См. Также

tsort, Unix-программу для топологической сортировки
Набор дуг обратной связи, набор ребер, удаление которых позволяет топологически отсортировать оставшийся подграф
алгоритм сильносвязных компонентов, алгоритм, который выдает топологически отсортированный список сильно связанных компонентов в графе
Предпотопологический порядок

Примечания

Ссылки

Кук, Стивен А. (1985), «Таксономия проблем с быстрыми параллельными алгоритмами», Информация и управление, 64 (1–3): 2–22, doi : 10.1016 / S0019-9958 (85) 80041-3.
Кормен, Томас Х. ; Лейзерсон, Чарльз Э. ; Ривест, Рональд Л. ; Стейн, Клиффорд (2001), «Раздел 22.4: Топологическая сортировка», Введение в алгоритмы (2-е изд.), MIT Press and McGraw-Hill, pp. 549–552, ISBN 0-262-03293-7.
Декель, Элиэзер; Нассими, Дэвид; Сахни, Сартадж (1981), «Параллельные алгоритмы матриц и графов», SIAM Journal on Computing, 10 (4): 657–675, doi : 10.1137 / 0210049, MR 0635424.
Ярнагин, MP (1960), Автоматические методы тестирования сетей PERT на непротиворечивость, Технический меморандум № K-24/60, Дальгрен, Вирджиния: Лаборатория военно-морского вооружения США.
Кан, Артур Б. ( 1962), «Топологическая сортировка больших сетей», Коммуникации ACM, 5 (11): 558–562, doi : 10.1145 / 368996.369025, S2CID 16728233.
Сандерс, Питер; Мельхорн, Курт; Дицфельбингер, Мартин; Дементьев, Роман (2019), Последовательные и параллельные алгоритмы и структуры данных: The Basic Toolbox, Springer International Publishing, ISBN 978-3-030-25208-3.
Спивак, Дэвид И. (2014), Теория категорий для наук, MIT Press.
Тарьян, Роберт Э. (1976), «Остовные деревья с непересекающимися краями и поиск в глубину», Acta Informatica, 6 (2): 171–185, doi : 10.1007 / BF00268499, S2CID 12044793.
Вернет, Освальдо; Маркензон, Лилиан (1997), "Гамильтоновы задачи для приводимых потоков-графов", Proc. 17-я Международная конференция Чилийского общества компьютерных наук (SCCC '97) (PDF), стр. 264–267, doi : 10.1109 / SCCC.1997.637099, hdl : 11422/2585, S2CID 206554481.

Дополнительная литература

D. Э. Кнут, Искусство компьютерного программирования, Том 1, раздел 2.2.3, в котором дается алгоритм топологической сортировки частичного упорядочения и краткая история.