Конечная скорость

редактировать

Сила тяжести, направленная вниз (F g), равна сдерживающей силе сопротивления (F d) плюс плавучесть. Чистая сила, действующая на объект, равна нулю, и в результате скорость объекта остается постоянной.

Конечная скорость - это максимальная скорость, достигаемая объектом при падении через жидкость (air - самый распространенный пример). Это происходит, когда сумма силы сопротивления (F d) и плавучести равна направляемой вниз силе силы тяжести (FG), действующей на объекте. Поскольку чистая сила на объекте равна нулю, объект имеет нулевое ускорение.

В гидродинамике объект движется со своей конечной скоростью, если его скорость постоянна из-за сдерживающей силы, оказываемой жидкостью, в которой она движется.

С увеличением скорости объекта увеличивается и сила сопротивления, действующая на него, которая также зависит от вещества, через которое он проходит (например, воздуха или воды). На некоторой скорости сопротивление или сила сопротивления будут равны гравитационному притяжению объекта (плавучесть рассматривается ниже). В этот момент объект перестает ускоряться и продолжает падать с постоянной скоростью, называемой конечной скоростью (также называемой скоростью установления). Объект, движущийся вниз со скоростью, превышающей предельную (например, потому что он был брошен вниз, упал из более тонкой части атмосферы или изменил форму), будет замедляться, пока не достигнет предельной скорости. Перетаскивание зависит от области проекции, в данном случае от поперечного сечения или силуэта объекта в горизонтальной плоскости. Объект с большой площадью проецирования относительно его массы, например парашют, имеет меньшую конечную скорость, чем объект с небольшой площадью проецирования относительно его массы, например дротик. В общем, для той же формы и материала конечная скорость объекта увеличивается с размером. Это потому, что направленная вниз сила (вес) пропорциональна кубу линейного размера, но сопротивление воздуха приблизительно пропорционально площади поперечного сечения, которая увеличивается только как квадрат линейного размера. Для очень маленьких объектов, таких как пыль и туман, конечная скорость легко преодолевается конвекционными потоками, которые не позволяют им достигать земли, и, следовательно, они остаются в воздухе в течение неопределенного времени. Загрязнение воздуха и туман являются примерами этого.

Содержание

1 Примеры
2 Физика
- 2.1 Вывод для конечной скорости
- 2.2 Конечная скорость в ползущем потоке
  - 2.2.1 Приложения
3 Конечная скорость при наличии плавучести force
4 См. также
5 Ссылки
6 Внешние ссылки

Примеры

График зависимости скорости парашютиста от времени, достигающего предельной скорости.

На основе сопротивления ветра, например, Предельная скорость парашютиста в положении «живот к земле» (т. е. лицом вниз) свободное падение составляет около 195 км / ч (120 миль / ч ; 54 м / с ). Эта скорость является асимптотическим предельным значением скорости, и силы, действующие на тело, уравновешивают друг друга все более и более по мере приближения к конечной скорости. В этом примере скорость 50% от скорости терминала достигается всего за 3 секунды, в то время как для достижения 90% требуется 8 секунд, для достижения 99% - 15 секунд и так далее.

Более высокая скорость может быть достигнута, если парашютист тянет свои конечности (см. Также свободный полет ). В этом случае конечная скорость увеличивается примерно до 320 км / ч (200 миль / ч или 90 м / с), что почти равно конечной скорости сапсана, ныряющего на свою добычу. Такая же конечная скорость достигается для типичной пули .30-06, падающей вниз - когда она возвращается на землю после выстрела вверх или падения с башни - согласно исследованию артиллерийского вооружения армии США 1920 года.

Соревнования парашютисты-парашютисты летают вниз головой и могут развивать скорость 530 км / ч (330 миль / ч; 150 м / с); текущий рекорд принадлежит Феликсу Баумгартнеру, который прыгнул с высоты 128 100 футов (39 000 м) и достиг 1357,6 км / ч (840 миль / ч; 380 м / с), хотя он достиг этой скорости на большой высоте. где плотность воздуха намного ниже, чем у поверхности Земли, поэтому создается низкая сила сопротивления.

Биолог Дж. Б. С. Холдейн писал:

Для мыши и любого более мелкого животного [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий шок и уходит. Убита крыса, сломан человек, брызжет конь. Поскольку сопротивление, оказываемое движению воздуха, пропорционально поверхности движущегося объекта.

Физика

Используя математические термины, конечная скорость - без учета эффектов плавучести - определяется выражением

V t = 2 мг ρ AC d {\ displaystyle V_ {t} = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}}}

{\ displaystyle V_ {t} = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}}}

где

$V t {\ displaystyle V_ {t}}$ $V_ {t}$ представляет конечную скорость,
$m {\ displaystyle m}$ $m$ - масса падающего объекта,
$g { \ displaystyle g}$ $g$ - это ускорение свободного падения,
$C d {\ displaystyle C_ {d}}$ $C_ {d}$ - коэффициент сопротивления,
$ρ { \ displaystyle \ rho}$ $\ rho$ - плотность жидкости, через которую падает объект, а
$A {\ displaystyle A}$ $A$ - площадь проецирования объекта.

В действительности объект приближается к своей конечной скорости асимптотически.

Эффекты плавучести из-за направленной вверх силы, действующей на объект окружающей жидкостью, могут быть приняты во внимание используя Arc Принцип Химеда : масса $m {\ displaystyle m}$ $m$ должна быть уменьшена на массу вытесненной жидкости $ρ V {\ displaystyle \ rho V}$ $\ rho V$ с $V {\ displaystyle V}$ $V$ объемом объекта. Поэтому вместо $m {\ displaystyle m}$ $m$ используйте приведенную массу $mr = m - ρ V {\ displaystyle m_ {r} = m- \ rho V}$ ${\ displaystyle m_ {r} = m- \ rho V}$ в этой и последующих формулах.

Конечная скорость объекта изменяется из-за свойств жидкости, массы объекта и его проекции поперечного сечения площадь поверхности.

Плотность воздуха увеличивается с уменьшением высоты, примерно на 1 % на 80 метров (260 футов) (см. барометрическую формулу ). Для объектов, падающих через атмосферу, на каждые 160 метров (520 футов) падения конечная скорость уменьшается на 1%. После достижения локальной конечной скорости, продолжая падение, скорость уменьшается, чтобы измениться с локальной конечной скоростью.

Вывод для предельной скорости

Используя математические термины, определяя вниз как положительное, результирующая сила, действующая на объект, падающий вблизи поверхности Земли, равна (согласно уравнению сопротивления ):

F net = ma = mg - 1 2 ρ v 2 AC d, {\ displaystyle F_ {net} = ma = mg- {1 \ over 2} \ rho v ^ {2} AC_ {d },}

{\ displaystyle F_ {net} = ma = mg- {1 \ over 2} \ rho v ^ {2} AC_ {d},}

с v (t) скорость объекта как функция времени t.

В равновесии, чистая сила равна нулю (F net = 0), и скорость становится конечной скоростью. t → ∞ v (t) = V t:

мг - 1 2 ρ V t 2 AC d = 0. {\ displaystyle mg- {1 \ over 2} \ rho V_ {t} ^ {2} AC_ {d} = 0.}

{\ displaystyle mg- {1 \ over 2} \ rho V_ {t} ^ {2} AC_ {d} = 0.}

Решение для V t дает

(5)

V t = 2 мг ρ AC d. {\ displaystyle V_ {t} = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}}.}

{\ displaystyle V_ {t} = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}}.}

Вывод решения для скорости v как функции времени t
Уравнение сопротивления - при условии, что ρ, g и C d являются постоянными: $ma = mdvdt = mg - 1 2 ρ v 2 AC d. {\ displaystyle ma = m {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = mg - {\ frac {1} {2}} \ rho v ^ {2} AC_ {d}.}$ ${\ displaystyle ma = m {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = mg - {\ frac {1} {2}} \ rho v ^ {2} AC_ {d}.}$ Хотя это уравнение Риккати, которое может быть решено путем сведения к линейному дифференциальному уравнению второго порядка, легче разделить переменные. Более практичная форма этого Уравнение может быть получено заменой α = ρAC d / 2mg. Деление обеих сторон на m дает $d v d t = g (1 - α 2 v 2). {\ displaystyle {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = g \ left (1- \ alpha ^ {2} v ^ {2} \ right).}$ ${\ displaystyle {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = g \ left (1- \ alpha ^ {2} v ^ {2} \ right).}$ уравнение может быть преобразовано в $dt = dvg (1 - α 2 v 2). {\ displaystyle \ mathrm {d} t = {\ frac {\ mathrm {d} v} {g (1- \ alpha ^ {2} v ^ {2})}}.}$ ${ \ displaystyle \ mathrm {d} t = {\ frac {\ mathrm {d} v} {g (1- \ alpha ^ {2} v ^ {2})}}.}$ Взяв интеграл от обоих сторон дает $∫ 0 tdt ′ = 1 g ∫ 0 vdv ′ 1 - α 2 v ′ 2. {\ displaystyle \ int _ {0} ^ {t} {\ mathrm {d} t ^ {\ prime}} = {1 \ over g} \ int _ {0} ^ {v} {\ frac {\ mathrm { d} v ^ {\ prime}} {1- \ alpha ^ {2} v ^ {\ prime 2}}}.}$ ${ \ displaystyle \ int _ {0} ^ {t} {\ mathrm {d} t ^ {\ prime}} = {1 \ over g} \ int _ {0} ^ {v} {\ frac {\ mathrm {d } v ^ {\ prime}} {1- \ alpha ^ {2} v ^ {\ prime 2}}}.}$ После интегрирования это становится $t - 0 = 1 g [ln ⁡ ( 1 + α v ′) 2 α - ln ⁡ (1 - α v ′) 2 α + C] v ′ = 0 v ′ = v = 1 g [ln ⁡ 1 + α v ′ 1 - α v ′ 2 α + C] v '= 0 v' = v {\ displaystyle t-0 = {1 \ over g} \ left [{\ ln (1+ \ alpha v ^ {\ prime}) \ over 2 \ alpha} - {\ гидроразрыв {\ ln (1- \ alpha v ^ {\ prime})} {2 \ alpha}} + C \ right] _ {v ^ {\ prime} = 0} ^ {v ^ {\ prime} = v} = {1 \ over g} \ left [{\ ln {\ frac {1+ \ alpha v ^ {\ prime}} {1- \ alpha v ^ {\ prime}}} \ over 2 \ alpha} + C \ справа] _ {v ^ {\ prime} = 0} ^ {v ^ {\ prime} = v}}$ $t-0 = {1 \ над g} \ left [{\ ln (1+ \ alpha v ^ {\ prime}) \ over 2 \ alpha} - {\ frac {\ ln (1- \ alpha v ^ {\ prime})} {2 \ alpha}} + C \ right] _ {{v ^ {\ prime} = 0}} ^ {{v ^ {\ prime} = v}} = {1 \ over g} \ left [{\ ln {\ frac {1+ \ alpha v ^ {\ prime}} {1- \ alpha v ^ {\ prime}}} \ over 2 \ alpha} + C \ right] _ {{v ^ {\ prime} = 0}} ^ {{v ^ {\ prime} = v}}$ или в более простой форме $t = 1 2 α g ln ⁡ 1 + α v 1 - α v знак равно arctanh (α v) α g, {\ displaystyle t = {1 \ over 2 \ alpha g} \ ln {\ frac {1+ \ alpha v} {1- \ alpha v}} = {\ frac { \ mathrm {arctanh} (\ alpha v)} {\ alpha g}},}$ ${\ displaystyle t = {1 \ over 2 \ alpha g} \ ln {\ frac {1+ \ alpha v} {1- \ alpha v}} = {\ frac {\ mathrm {arctanh} (\ alpha v)} {\ alpha g}},}$ с arctanh функция обратного гиперболического тангенса. В качестве альтернативы $1 α tanh ⁡ (α gt) = v, {\ displaystyle {\ frac {1} {\ alpha}} \ tanh (\ alpha gt) = v,}$ ${\ displaystyle {\ гидроразрыв {1} {\ alpha}} \ tanh (\ alpha gt) = v,}$ с tanh функция гиперболический тангенс. Предполагая, что g положительно (что было определено как), и подставляя обратно α, скорость v становится $v = 2 m g ρ A C d tanh ⁡ (t g ρ A C d 2 m). {\ displaystyle v = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}} \ tanh \ left (t {\ sqrt {\ frac {g \ rho AC_ {d}} {2m}}}) \ right).}$ ${\ displaystyle v = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}} \ tanh \ left (t {\ sqrt {\ frac {g \ rho AC_ {d}} {2m}}} \ right).}$ Когда время стремится к бесконечности (t → ∞), гиперболический тангенс стремится к 1, в результате чего конечная скорость $V t = lim t → ∞ v (t) = 2 mg ρ AC d. {\ displaystyle V_ {t} = \ lim _ {t \ to \ infty} v (t) = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}}.}$ ${\ displaystyle V_ {t} = \ lim _ {t \ to \ infty} v (t) = {\ sqrt {\ frac {2mg} {\ rho AC_ { d}}}}.}$

Вывод решения для скорости v как функции времени t

Уравнение сопротивления - при условии, что ρ, g и C d являются постоянными:

ma = mdvdt = mg - 1 2 ρ v 2 AC d. {\ displaystyle ma = m {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = mg - {\ frac {1} {2}} \ rho v ^ {2} AC_ {d}.}

{\ displaystyle ma = m {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = mg - {\ frac {1} {2}} \ rho v ^ {2} AC_ {d}.}

Хотя это уравнение Риккати, которое может быть решено путем сведения к линейному дифференциальному уравнению второго порядка, легче разделить переменные.

Более практичная форма этого Уравнение может быть получено заменой α = ρAC d / 2mg.

Деление обеих сторон на m дает

d v d t = g (1 - α 2 v 2). {\ displaystyle {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = g \ left (1- \ alpha ^ {2} v ^ {2} \ right).}

{\ displaystyle {\ frac {\ mathrm {d} v} {\ mathrm {d} t}} = g \ left (1- \ alpha ^ {2} v ^ {2} \ right).}

уравнение может быть преобразовано в

dt = dvg (1 - α 2 v 2). {\ displaystyle \ mathrm {d} t = {\ frac {\ mathrm {d} v} {g (1- \ alpha ^ {2} v ^ {2})}}.}

{ \ displaystyle \ mathrm {d} t = {\ frac {\ mathrm {d} v} {g (1- \ alpha ^ {2} v ^ {2})}}.}

Взяв интеграл от обоих сторон дает

∫ 0 tdt ′ = 1 g ∫ 0 vdv ′ 1 - α 2 v ′ 2. {\ displaystyle \ int _ {0} ^ {t} {\ mathrm {d} t ^ {\ prime}} = {1 \ over g} \ int _ {0} ^ {v} {\ frac {\ mathrm { d} v ^ {\ prime}} {1- \ alpha ^ {2} v ^ {\ prime 2}}}.}

{ \ displaystyle \ int _ {0} ^ {t} {\ mathrm {d} t ^ {\ prime}} = {1 \ over g} \ int _ {0} ^ {v} {\ frac {\ mathrm {d } v ^ {\ prime}} {1- \ alpha ^ {2} v ^ {\ prime 2}}}.}

После интегрирования это становится

t - 0 = 1 g [ln ⁡ ( 1 + α v ′) 2 α - ln ⁡ (1 - α v ′) 2 α + C] v ′ = 0 v ′ = v = 1 g [ln ⁡ 1 + α v ′ 1 - α v ′ 2 α + C] v '= 0 v' = v {\ displaystyle t-0 = {1 \ over g} \ left [{\ ln (1+ \ alpha v ^ {\ prime}) \ over 2 \ alpha} - {\ гидроразрыв {\ ln (1- \ alpha v ^ {\ prime})} {2 \ alpha}} + C \ right] _ {v ^ {\ prime} = 0} ^ {v ^ {\ prime} = v} = {1 \ over g} \ left [{\ ln {\ frac {1+ \ alpha v ^ {\ prime}} {1- \ alpha v ^ {\ prime}}} \ over 2 \ alpha} + C \ справа] _ {v ^ {\ prime} = 0} ^ {v ^ {\ prime} = v}}

t-0 = {1 \ над g} \ left [{\ ln (1+ \ alpha v ^ {\ prime}) \ over 2 \ alpha} - {\ frac {\ ln (1- \ alpha v ^ {\ prime})} {2 \ alpha}} + C \ right] _ {{v ^ {\ prime} = 0}} ^ {{v ^ {\ prime} = v}} = {1 \ over g} \ left [{\ ln {\ frac {1+ \ alpha v ^ {\ prime}} {1- \ alpha v ^ {\ prime}}} \ over 2 \ alpha} + C \ right] _ {{v ^ {\ prime} = 0}} ^ {{v ^ {\ prime} = v}}

или в более простой форме

t = 1 2 α g ln ⁡ 1 + α v 1 - α v знак равно arctanh (α v) α g, {\ displaystyle t = {1 \ over 2 \ alpha g} \ ln {\ frac {1+ \ alpha v} {1- \ alpha v}} = {\ frac { \ mathrm {arctanh} (\ alpha v)} {\ alpha g}},}

{\ displaystyle t = {1 \ over 2 \ alpha g} \ ln {\ frac {1+ \ alpha v} {1- \ alpha v}} = {\ frac {\ mathrm {arctanh} (\ alpha v)} {\ alpha g}},}

с arctanh функция обратного гиперболического тангенса.

В качестве альтернативы

1 α tanh ⁡ (α gt) = v, {\ displaystyle {\ frac {1} {\ alpha}} \ tanh (\ alpha gt) = v,}

{\ displaystyle {\ гидроразрыв {1} {\ alpha}} \ tanh (\ alpha gt) = v,}

с tanh функция гиперболический тангенс. Предполагая, что g положительно (что было определено как), и подставляя обратно α, скорость v становится

v = 2 m g ρ A C d tanh ⁡ (t g ρ A C d 2 m). {\ displaystyle v = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}} \ tanh \ left (t {\ sqrt {\ frac {g \ rho AC_ {d}} {2m}}}) \ right).}

{\ displaystyle v = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}} \ tanh \ left (t {\ sqrt {\ frac {g \ rho AC_ {d}} {2m}}} \ right).}

Когда время стремится к бесконечности (t → ∞), гиперболический тангенс стремится к 1, в результате чего конечная скорость

V t = lim t → ∞ v (t) = 2 mg ρ AC d. {\ displaystyle V_ {t} = \ lim _ {t \ to \ infty} v (t) = {\ sqrt {\ frac {2mg} {\ rho AC_ {d}}}}.}

{\ displaystyle V_ {t} = \ lim _ {t \ to \ infty} v (t) = {\ sqrt {\ frac {2mg} {\ rho AC_ { d}}}}.}

Конечная скорость в ползущий поток

ползущий поток мимо сферы: линии тока, сила сопротивления F d и сила тяжести F g

Для очень медленного движения жидкости силы инерции жидкости незначительны (предположение безмассовой жидкости) по сравнению с другими силами. Такие потоки называются ползущими потоками, и условие, которое должно выполняться для потоков, которые должны быть ползучими потоками, - это число Рейнольдса, $R e ≪ 1 {\ displaystyle Re \ ll 1 }$ $Re \ ll 1$ . Уравнение движения для ползучего потока (упрощенное уравнение Навье – Стокса ) задается следующим образом:

∇ p = μ ∇ 2 v {\ displaystyle {\ mathbf {\ nabla}} p = \ mu \ nabla ^ {2} {\ mathbf {v}}}

{\ displaystyle {\ mathbf {\ nabla}} p = \ mu \ nabla ^ {2} {\ mathbf {v}}}

где

$v {\ displaystyle {\ mathbf {v}}}$ ${\ mathbf {v}}$ - векторное поле скорости жидкости,
$p {\ displaystyle p}$ $p$ - поле давления жидкости,
$μ {\ displaystyle \ mu}$ $\ mu$ - жидкость \ жидкость вязкость.

Аналитическое решение для ползучего потока вокруг сферы был впервые дан Стокса в 1851 году. Из решения Стокса сила сопротивления, действующая на сферу, может быть получена как

(6) D = 3 π μ d V или C d = 24 R е {\ Displaystyle \ quad (6) \ qquad D = 3 \ pi \ mu dV \ qquad \ qquad {\ text {или}} \ qquad \ qquad C_ {d} = {\ frac {24} {Re} }}

\ quad (6) \ qquad D = 3 \ pi \ mu dV \ qquad \ qquad {\ text {или}} \ qquad \ qquad C_ {d} = {\ frac {24} {Re}}

где число Рейнольдса, $R e = 1 μ ρ d V {\ displaystyle Re = {\ frac {1} {\ mu}} \ rho dV}$ $Re = {\ frac {1} { \ mu}} \ rho dV$ . Выражение для силы лобового сопротивления, задаваемое уравнением (6), называется законом Стокса.

, когда значение $C d {\ displaystyle C_ {d}}$ $C_ {d}$ подставляется в уравнение (5), мы получаем выражение для предельной скорости сферического объекта, движущегося в условиях ползучего потока:

V t = gd 2 18 μ (ρ s - ρ), {\ displaystyle V_ {t} = {\ frac {gd ^ {2}} {18 \ mu}} \ left (\ rho _ {s} - \ rho \ right),}

{\ displaystyle V_ {t} = {\ frac {gd ^ {2}} {18 \ mu}} \ left (\ rho _ {s} - \ rho \ right),}

где $ρ s {\ displaystyle \ rho _ {s}}$ $\ rho_s$ - плотность объекта.

Приложения

Результаты ползучего потока могут применяться для изучения осаждения отложений у дна океана и падения капель влаги в атмосфере. Этот принцип также применяется в вискозиметре с падающей сферой, экспериментальном устройстве, используемом для измерения вязкости высоковязких жидкостей, например нефти, парафина, гудрона и т. Д.

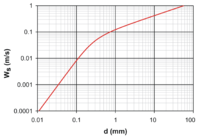Конечная скорость в присутствии выталкивающей силы

Скорость оседания W s песчинки (диаметр d, плотность 2650 кг / м) в воде при 20 ° C, вычисленная по формуле Soulsby (1997).

Если принять во внимание эффекты плавучести, объект, падающий через жидкость под собственным весом, может достичь предельной скорости (скорости оседания), если результирующая сила, действующая на объект, станет равной нулю. Когда достигается предельная скорость, вес объекта точно уравновешивается восходящей силой плавучести и силой сопротивления. То есть

(1) W = F b + D {\ displaystyle \ quad (1) \ qquad W = F_ {b} + D}

\ quad (1) \ qquad W = F_ {b} + D

, где

$W {\ displaystyle W}$ $W$ = вес объекта,
$F b {\ displaystyle F_ {b}}$ $F_{b}$ = сила плавучести, действующая на объект, и
$D {\ displaystyle D}$ $D$ = сила сопротивления, действующая на объект.

Если падающий объект имеет сферическую форму, выражения для трех сил приведены ниже:

(2) W = π 6 d 3 ρ sg, (3) F б знак равно π 6 d 3 ρ г, (4) D знак равно C d 1 2 ρ V 2 A, {\ Displaystyle {\ begin {align} \ quad (2) \ qquad W = {\ frac {\ pi} { 6}} d ^ {3} \ rho _ {s} g, \\\ quad (3) \ qquad F_ {b} = {\ frac {\ pi} {6}} d ^ {3} \ rho g, \\\ quad (4) \ qquad D = C_ {d} {\ frac {1} {2}} \ rho V ^ {2} A, \ end {align}}}

{ \ Displaystyle {\ begin {align} \ quad (2) \ qquad W = {\ frac {\ pi} {6}} d ^ {3} \ rho _ {s} g, \\ \ quad (3) \ qquad F_ {b} = {\ frac {\ pi} {6}} d ^ {3} \ rho g, \\\ quad (4) \ qquad D = C_ {d} {\ frac {1} {2}} \ rho V ^ {2} A, \ end {align}}}

где

$d {\ displaystyle d}$ $d$ - диаметр сферического объекта,
$g {\ displaystyle g}$ $g$ - ускорение свободного падения,
$ρ {\ displaystyle \ rho }$ $\ rho$ - плотность жидкости,
$ρ s {\ displaystyle \ rho _ {s}}$ $\ rho_s$ - плотность объекта,
$A = 1 4 π d 2 {\ displaystyle A = {\ frac {1} {4}} \ pi d ^ {2}}$ $A = {\ frac {1} {4}} \ pi d ^ {2}$ - площадь проекции сферы,
$C d {\ displaystyle C_ { d}}$ $C_ {d}$ - коэффициент лобового сопротивления, а
$V {\ displaystyle V}$ $V$ - характеристическая скорость (принятая как конечная скорость, $V t {\ displaystyle V_ { t}}$ $V_ {t}$ ).

Подстановка уравнений (2–4) в уравнение (1) и решение для конечной скорости, $V t {\ displaystyle V_ {t}}$ $V_ {t}$ , чтобы получить следующее выражение

(5) V t = 4 gd 3 C d (ρ s - ρ ρ). {\ displaystyle \ quad (5) \ qquad V_ {t} = {\ sqrt {{\ frac {4gd} {3C_ {d}}} \ left ({\ frac {\ rho _ {s} - \ rho} { \ rho}} \ right)}}.}

{\ displaystyle \ quad (5) \ qquad V_ {t} = {\ sqrt {{\ frac {4gd} {3C_ {d}}} \ left ({\ frac {\ rho _ {s} - \ rho} {\ rho}} \ right)}}.}

В уравнении (1) предполагается, что объект более плотный, чем жидкость. В противном случае знак силы сопротивления следует сделать отрицательным, поскольку объект будет двигаться вверх против силы тяжести. Примерами являются пузырьки, образующиеся на дне бокала с шампанским, и воздушные шары с гелием. Конечная скорость в таких случаях будет иметь отрицательное значение, соответствующее скорости подъема.

См. Также

Ссылки

Внешние ссылки

Конечная скорость - сайт НАСА
Бортовое видео Space Shuttle Solid Ракетные ускорители быстро замедляются до предельной скорости при входе в более плотную атмосферу, с 2900 миль в час (3,8 Маха) в 5:15 на видео до 220 миль в час в 6:45, когда парашюты раскрываются через 90 секунд - Видео и звук НАСА, @ io9.com.