Войти
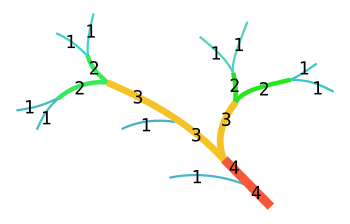
Диаграмма, показывающая порядок потоков Strahler В математике число Стрелера или число Хортона – Стрелера математического дерева является числовой мерой его сложности ветвления.
Эти цифры были впервые разработаны в гидрология по Роберту Хортон ( 1945) и Артур Newell Strahler ( 1952, 1957); в этой заявке, они упоминаются как для того поток Strahler и используются для определения размера потока на основе иерархии притоков. Они также возникают при анализе L-систем и иерархических биологических структур, таких как (биологические) деревья, дыхательные и кровеносные системы животных, при распределении регистров для компиляции языков программирования высокого уровня и при анализе социальных сетей. Альтернативные системы упорядочивания потоков были разработаны Shreve и Hodgkinson et al. Смарт дает статистическое сравнение систем Strahler и Shreve, а также анализ длин потоков / каналов.
Все деревья в этом контексте являются ориентированными графами, ориентированными от корня к листьям; другими словами, это древовидные растения. Степень узла в дереве только его количество детей. Можно присвоить номер Strahler всем узлам дерева в восходящем порядке следующим образом:
Число Стрелера дерева - это номер его корневого узла.
Алгоритмически эти номера могут быть присвоены путем выполнения поиска в глубину и присвоения номера каждого узла в поступорядочении. Те же числа могут также быть сгенерированы посредством процесса отсечения, в котором дерево упрощается в последовательности этапов, где на каждом этапе удаляются все конечные узлы и все пути узлов первой степени, ведущие к листьям: число Стрелера для узел - это этап, на котором он будет удален этим процессом, а число Стрелера дерева - это количество этапов, необходимых для удаления всех его узлов. Другое эквивалентное определение числа Стрелера дерева состоит в том, что это высота наибольшего полного двоичного дерева, которое может быть гомеоморфно вложено в данное дерево; Число Стрелера узла в дереве аналогично высоте самого большого полного двоичного дерева, которое может быть встроено под этот узел.
Любой узел с номером Strahler i должен иметь не менее двух потомков с номером Strahler i - 1, не менее четырех потомков с номером Strahler i - 2 и т. Д. И не менее 2 i - 1 листовых потомков. Следовательно, в дереве с n узлами максимально возможное число Стрелера равно log 2 n + 1. Однако, если дерево не образует полное двоичное дерево, его число Стрелера будет меньше этой границы. В двоичном дереве с n узлами, выбранном равномерно случайным образом среди всех возможных двоичных деревьев, ожидаемый индекс корня с высокой вероятностью очень близок к log 4 n.
В применении к гидрологии порядка потока Стрелера каждый сегмент потока или реки в речной сети рассматривается как узел в дереве, а следующий сегмент ниже по течению является его родительским. Когда два потока первого порядка объединяются, они образуют поток второго порядка. Когда два потока второго порядка объединяются, они образуют поток третьего порядка. Потоки более низкого порядка, присоединяющиеся к потоку более высокого порядка, не изменяют порядок потока более высокого порядка. Таким образом, если поток первого порядка присоединяется к потоку второго порядка, он остается потоком второго порядка. Только когда поток второго порядка объединяется с другим потоком второго порядка, он становится потоком третьего порядка. Как и в случае с математическими деревьями, сегмент с индексом i должен питаться по крайней мере 2 i - 1 различными притоками индекса 1. Шрив заметил, что законы Хортона и Стрелера следует ожидать от любого топологически случайного распределения. Более поздний обзор взаимосвязей подтвердил этот аргумент, установив, что из свойств, описываемых законами, нельзя сделать никаких выводов, объясняющих структуру или происхождение потоковой сети.
Чтобы считаться ручьем, гидрологический объект должен быть либо повторяющимся, либо постоянным. Регулярные (или «прерывистые») ручьи имеют воду в русле, по крайней мере, часть года. Индекс потока или реки может варьироваться от 1 (ручей без притоков) до 12 (самая мощная река в мире, Амазонка, в ее устье). Река Огайо имеет восьмой порядок, а река Миссисипи - десятого порядка. По оценкам, 80% водотоков на планете являются верховьями от первого до третьего порядка.
Если коэффициент бифуркации речной сети низкий, то вероятность наводнения выше, поскольку вода будет концентрироваться в одном русле, а не распространяться, как указывает более высокий коэффициент бифуркации. Соотношение бифуркации также может показать, какие части водосборного бассейна с большей вероятностью будут затоплены, сравнительно, если посмотреть на отдельные коэффициенты. У большинства британских рек коэффициент бифуркации составляет от 3 до 5.
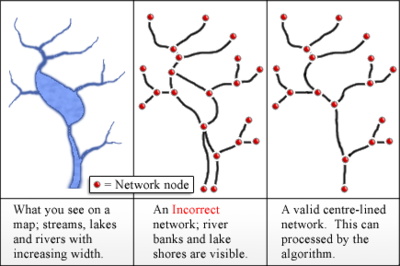Сравнение неправильного и правильного преобразования водоемов в древовидную сеть Gleyzer et al. (2004) описывают, как вычислить значения порядка потока Strahler в приложении ГИС. Этот алгоритм реализован RivEX, инструментом ESRI ArcGIS 10.6.1. Входом в их алгоритм является сеть осевых линий водоемов, представленных в виде дуг (или ребер), соединенных в узлах. Границы озер и берега рек не следует использовать в качестве дуг, так как они обычно образуют сеть без деревьев с неправильной топологией.
Нумерация Strahler может применяться при статистическом анализе любой иерархической системы, а не только рек.
При переводе языка программирования высокого уровня на ассемблере минимальное количество регистров необходимо оценить выражение дерева именно его номер Strahler. В этом контексте номер Strahler также может называться номером регистра.
Для деревьев выражений, требующих большего количества регистров, чем доступно, алгоритм Сетхи-Уллмана может использоваться для преобразования дерева выражений в последовательность машинных инструкций, которые максимально эффективно используют регистры, сводя к минимуму количество раз, когда промежуточные значения выводятся из регистров. в основную память и общее количество инструкций в результирующем скомпилированном коде.
С числами Стрелера дерева связаны коэффициенты бифуркации, числа, описывающие, насколько дерево близко к сбалансированному. Для каждого порядка i в иерархии коэффициент бифуркации i равен
где n i обозначает количество узлов с порядком i.
Коэффициент бифуркации всей иерархии может быть получен путем усреднения коэффициентов бифуркации в различных порядках. В полном двоичном дереве коэффициент бифуркации будет равен 2, в то время как другие деревья будут иметь более высокие коэффициенты бифуркации. Это безразмерное число.
Pathwidth произвольного неориентированного графа G может быть определена как наименьшее число ш такое, что существует интервал графа H, содержащий G в качестве подграфа, с наибольшей клики в H, имеющей ш + 1 вершин. Для деревьев (рассматриваемых как неориентированные графы, забывая об их ориентации и корне) ширина пути отличается от числа Стрелера, но тесно связана с ним: в дереве с шириной пути w и числом Стрелера s эти два числа связаны между собой неравенствами
Возможность обрабатывать графы с циклами, а не только с деревьями, дает дополнительную гибкость по сравнению с числом Стрелера. Однако, в отличие от числа Strahler, ширина пути определяется только для всего графа, а не отдельно для каждого узла в графе.
