Сферичность

Схематическое изображение разницы в форме зерна. Показаны два параметра: сферичность (по вертикали) и округление (по горизонтали).

Сферичность - это мера того, насколько близко форма объекта напоминает форму идеальной сферы . Например, сферичность шариков внутри шарикового подшипника определяет качество подшипника, такое как нагрузка, которую он может выдержать, или скорость, с которой он может повернуть без сбоев. Сферичность - это конкретный пример меры компактности формы. Определенная Уоделлом в 1935 году сферичность, $\Psi \; \{\backslash \; displaystyle\; \backslash \; Psi\}$, частицы - это отношение площади поверхности сферы того же объема, что и от данной частицы к площади поверхности частицы:

$\Psi \; =\; \pi \; 1\; 3\; (6\; V\; p)\; 2\; 3\; A\; p\; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\; \}\; (6V\_\; \{p\})\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}\; \{A\_\; \{p\}\}\}\}$

где $V\; p\; \{\backslash \; displaystyle\; V\_\; \{p\}\}$- объем частицы, а $A\; p\; \{\backslash \; displaystyle\; A\_\; \{p\}\}$- площадь поверхности частицы. Сферичность сферы по определению равна единице, и в соответствии с изопериметрическим неравенством любая частица, не являющаяся сферой, будет иметь сферичность меньше 1.

Применяется сферичность в трех измерениях ; его аналог в двухмерном, такой как поперечное сечение окружностей вдоль цилиндрического объекта, такого как вал, называется округлость.

• 1 Эллипсоидальные объекты
• 2 Получение
• 3 Сферичность общих объектов
• 4 См. также
• 5 Ссылки
• 6 Внешние ссылки

Сферичность, $\Psi \; \{\backslash \; displaystyle\; \backslash \; Psi\}$, сплющенного сфероида (похожего на форму планеты Земля ):

$\Psi \; знак\; равно\; \pi \; 1\; 3\; (6\; V\; p)\; 2\; 3\; A\; p\; =\; 2\; ab\; 2\; 3\; a\; +\; b\; 2\; a\; 2\; -\; b\; 2\; ln\; \; (a\; +\; a\; 2\; -\; b\; 2\; b),\; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; (6V\_\; \{p\})\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}\; \{A\_\; \{p\}\}\}\; =\; \{\backslash \; frac\; \{2\; \{\backslash \; sqrt\; [\{3\}]\; \{ab\; ^\; \{2\}\}\}\}\; \{a\; +\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\}\}\; \backslash \; ln\; \{\backslash \; left\; (\{\backslash \; frac\; \{a\; +\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\}\}\; \{b\}\}\; \backslash \; right)\}\}\},\}$

где a и b - полу- основная и малая полуоси соответственно.

Хакон Уоделл определил сферичность как площадь поверхности сферы того же объема, что и частица, деленная на фактическую площадь поверхности частицы.

Сначала нам нужно записать площадь поверхности сферы, $A\; s\; \{\backslash \; displaystyle\; A\_\; \{s\}\}$в единицах объема частицы, $V\; p\; \{\backslash \; displaystyle\; V\_\; \{p\}\}$

$A\; s\; 3\; =\; (4\; \pi \; r\; 2)\; 3\; =\; 4\; 3\; \pi \; 3\; r\; 6\; =\; 4\; \pi \; (4\; 2\; \pi \; 2\; r\; 6)\; =\; 4\; \pi \; \cdot \; 3\; 2\; (4\; 2\; \pi \; 2\; 3\; 2\; р\; 6)\; знак\; равно\; 36\; \pi \; (4\; \pi \; 3\; р\; 3)\; 2\; =\; 36\; \pi \; V\; p\; 2\; \{\backslash \; displaystyle\; A\_\; \{s\}\; ^\; \{3\}\; =\; \backslash \; left\; (4\; \backslash \; pi\; r\; ^\; \{2\}\; \backslash \; right)\; ^\; \{3\}\; =\; 4\; ^\; \{3\}\; \backslash \; pi\; ^\; \{3\}\; r\; ^\; \{6\}\; =\; 4\; \backslash \; pi\; \backslash \; left\; (4\; ^\; \{2\}\; \backslash \; pi\; ^\; \{2\}\; r\; ^\; \{6\}\; \backslash \; right)\; =\; 4\; \backslash \; pi\; \backslash \; cdot\; 3\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{4\; ^\; \{2\}\; \backslash \; pi\; ^\; \{2\}\}\; \{3\; ^\; \{2\}\}\}\; r\; ^\; \{6\}\; \backslash \; right)\; =\; 36\; \backslash \; pi\; \backslash \; left\; (\{\; \backslash \; frac\; \{4\; \backslash \; pi\}\; \{3\}\}\; r\; ^\; \{3\}\; \backslash \; right)\; ^\; \{2\}\; =\; 36\; \backslash ,\; \backslash \; pi\; V\_\; \{p\}\; ^\; \{2\}\}$

поэтому

$A\; s\; =\; (36\; \pi \; В\; п\; 2)\; 1\; 3\; =\; 36\; 1\; 3\; \pi \; 1\; 3\; В\; п\; 2\; 3\; =\; 6\; 2\; 3\; \pi \; 1\; 3\; В\; п\; 2\; 3\; =\; \pi \; 1\; 3\; (6\; В\; п)\; 2\; 3\; \{\backslash \; Displaystyle\; A\_\; \{s\}\; =\; \backslash \; left\; (36\; \backslash ,\; \backslash \; pi\; V\_\; \{p\}\; ^\; \{2\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; =\; 36\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; pi\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; V\_\; \{p\}\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; =\; 6\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; pi\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; V\_\; \{p\}\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; =\; \backslash \; pi\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; left\; (6V\_\; \{p\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}$

отсюда мы определяем $\Psi \; \{\backslash \; displaystyle\; \backslash \; Psi\}$как:

$\Psi \; =\; A\; s\; A\; p\; =\; \pi \; 1\; 3\; (6\; V\; p)\; 2\; 3\; A\; p\; \{\backslash \; dis\; playstyle\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{A\_\; \{s\}\}\; \{A\_\; \{p\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; left\; (6V\_\; \{p\}\; \backslash \; right)\; ^\; \{\; \backslash \; frac\; \{2\}\; \{3\}\}\}\; \{A\_\; \{p\}\}\}\}$

Имя	Изображение	Объем	Поверхность Площадь	Сферичность
Платоновы тела
тетраэдр		$2\; 12\; s\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\}\}\; \{12\}\}\; \backslash ,\; s\; ^\; \{3\}\}$	$3\; s\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{3\}\}\; \backslash ,\; s\; ^\; \{2\}\}$	$(\pi \; 6\; 3)\; 1\; 3\; \approx \; 0,671\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{6\; \{\backslash \; sqrt\; \{3\}\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,671\}$
куб (шестигранник)		$s\; 3\; \{\backslash \; displaystyle\; \backslash ,\; s\; ^\; \{\; 3\}\}$	$6\; s\; 2\; \{\backslash \; displaystyle\; 6\; \backslash ,\; s\; ^\; \{2\}\}$	$(\pi \; 6)\; 1\; 3\; \approx \; 0.806\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{6\}\}\; \backslash \; справа)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0.806\}$
октаэдр		$1\; 3\; 2\; s\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; \{2\}\}\; \backslash ,\; s\; ^\; \{3\}\}$	$2\; 3\; s\; 2\; \{\backslash \; displaystyle\; 2\; \{\backslash \; sqrt\; \{3\}\}\; \backslash ,\; s\; ^\; \{2\}\}$	$(\pi \; 3\; 3)\; 1\; 3\; \approx \; 0,846\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{3\; \{\backslash \; sqrt\; \{3\}\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,846\}$
додекаэдр		$1\; 4\; (15\; +\; 7\; 5)\; s\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; \backslash \; влево\; (15\; +\; 7\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\; \backslash ,\; s\; ^\; \{3\}\}$	$3\; 25\; +\; 10\; 5\; s\; 2\; \{\backslash \; displaystyle\; 3\; \{\backslash \; sqrt\; \{25\; +\; 10\; \{\backslash \; sqrt\; \{5\}\; \}\}\}\; \backslash ,\; s\; ^\; \{2\}\}$	$((15\; +\; 7\; 5)\; 2\; \pi \; 12\; (25\; +\; 10\; 5)\; 3\; 2)\; 1\; 3\; \approx \; 0,910\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; left\; (\; 15\; +\; 7\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; pi\}\; \{12\; \backslash \; left\; (25\; +\; 10\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\; \}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,910\}$
икосаэдр		$5\; 12\; (3\; +\; 5)\; s\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{5\}\; \{12\}\}\; \backslash \; left\; (3\; +\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\; \backslash ,\; s\; ^\; \{3\}\}$	$5\; 3\; s\; 2\; \{\backslash \; displaystyle\; 5\; \{\backslash \; sqrt\; \{3\}\}\; \backslash ,\; s\; ^\; \{2\}\}$	$((3\; +\; 5)\; 2\; \pi \; 60\; 3)\; 1\; 3\; \approx \; 0,939\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; left\; (3\; +\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; pi\}\; \{60\; \{\; \backslash \; sqrt\; \{3\}\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,939\}$
Круглые формы
идеальный конус. $(h\; =\; 2\; 2\; r)\; \{\; \backslash \; displaystyle\; (h\; =\; 2\; \{\backslash \; sqrt\; \{2\}\}\; r)\}$		$1\; 3\; \pi \; r\; 2\; h\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; pi\; \backslash ,\; r\; ^\; \{2\}\; h\}$. $=\; 2\; 2\; 3\; \pi \; r\; 3\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{2\; \{\backslash \; sqrt\; \{2\}\}\}\; \{3\}\}\; \backslash \; pi\; \backslash ,\; r\; ^\; \{3\}\}$	$\pi \; r\; (r\; +\; r\; 2\; +\; час\; 2)\; \{\backslash \; displaystyle\; \backslash \; pi\; \backslash ,\; r\; (r\; +\; \{\backslash \; sqrt\; \{r\; ^\; \{2\}\; +\; h\; ^\; \{2\}\}\})\}$. $=\; 4\; \pi \; r\; 2\; \{\backslash \; displaystyle\; =\; 4\; \backslash \; pi\; \backslash ,\; r\; ^\; \{2\}\}$	$(1\; 2)\; 1\; 3\; \approx \; 0,794\; \{\; \backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,794\}$
полусфера. (полусфера)		$2\; 3\; \pi \; р\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; pi\; \backslash ,\; r\; ^\; \{3\}\}$	$3\; \pi \; r\; 2\; \{\backslash \; displaystyle\; 3\; \backslash \; pi\; \backslash ,\; r\; ^\; \{2\}\}$	$(\; 16\; 27)\; 1\; 3\; \approx \; 0,840\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{16\}\; \{27\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,840\}$
идеальный цилиндр. 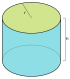$(час\; =\; 2\; р)\; \{\backslash \; displaystyle\; (час\; =\; 2\; \backslash ,\; r)\}$		$\pi \; r\; 2\; час\; =\; 2\; \pi \; r\; 3\; \{\backslash \; displaystyle\; \backslash \; pi\; r\; ^\; \{2\}\; h\; =\; 2\; \backslash \; pi\; \backslash ,\; r\; ^\; \{3\}\}$	$2\; \pi \; r\; (r\; +\; h)\; =\; 6\; \pi \; r\; 2\; \{\backslash \; displaystyle\; 2\; \backslash \; pi\; r\; (r\; +\; h)\; =\; 6\; \backslash \; pi\; \backslash ,\; r\; ^\; \{2\}\}$	$(2\; 3)\; 1\; 3\; \approx \; 0,874\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,874\}$
идеальный тор. $(R\; =\; r)\; \{\backslash \; displaystyle\; (R\; =\; r)\}$		$2\; \pi \; 2\; R\; r\; 2\; =\; 2\; \pi \; 2\; r\; 3\; \{\backslash \; displaystyle\; 2\; \backslash \; pi\; ^\; \{2\}\; Rr\; ^\; \{2\}\; =\; 2\; \backslash \; pi\; ^\; \{2\}\; \backslash ,\; r\; ^\; \{3\}\}$	$4\; \pi \; 2\; R\; r\; =\; 4\; \pi \; 2\; r\; 2\; \{\backslash \; displaystyle\; 4\; \backslash \; pi\; ^\; \{2\}\; Rr\; =\; 4\; \backslash \; pi\; ^\; \{2\}\; \backslash ,\; r\; ^\; \{2\; \}\}$	$(9\; 4\; \pi )\; 1\; 3\; \approx \; 0,894\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{9\}\; \{4\; \backslash \; pi\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 0,894\}$
сфера		$4\; 3\; \pi \; r\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash \; pi\; r\; ^\; \{3\}\}$	$4\; \pi \; r\; 2\; \{\backslash \; displ\; aystyle\; 4\; \backslash \; pi\; \backslash ,\; r\; ^\; \{2\}\}$	$1\; \{\backslash \; displaystyle\; 1\; \backslash ,\}$
Other Shapes
disdyakis triacontahedron		$180\; 11\; 179\; -\; 24\; 5\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{180\; \}\; \{11\}\}\; \{\backslash \; sqrt\; \{179-24\; \{\backslash \; sqrt\; \{5\}\}\}\}\}$	$180\; 11\; (5\; +\; 4\; 5)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{180\}\; \{11\}\}\; \backslash \; left\; (5\; +4\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\}$	$((5\; +\; 4\; 5)\; 2\; 11\; \pi \; 5)\; 1\; 3\; 179\; -\; 24\; 5\; \approx \; 0,986\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; left\; (\backslash \; left\; (5\; +4\; \{\backslash \; sqrt\; \{5\}\}\; \backslash \; right)\; ^\; \{2\}\; \{\backslash \; frac\; \{11\; \backslash \; pi\}\; \{5\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\}\; \{\backslash \; sqrt\; \{179-24\; \{\backslash \; sqrt\; \{5\}\}\}\}\}\; \backslash \; приблизительно\; 0,986\}$

• Эквивалентный сферический диаметр
• Сплющивание
• Изопериметрическое соотношение
• Округление (осадок)
• Willmore Energy

Поищите сферичность в Викисловаре, бесплатном словаре.

• Морфология зерен: округлость, особенности поверхности и сферичность зерен