Теорема оболочек

Утверждение о гравитационном притяжении сферических тел.

В классической механике, теорема оболочек дает гравитационные упрощения, которые могут применяться к объектам внутри или снаружи сферически симметричного тела. Эта теорема имеет особое приложение к астрономии.

Исаак Ньютон доказал теорему об оболочке и заявил, что:

1. A сферически симметричное тело воздействует на внешние объекты гравитационно, как если бы все его масса была сосредоточена в точке в ее центре.
2. Если тело представляет собой сферически-симметричную оболочку (т.е. полый шар), то нет гравитационной сила действует оболочкой на любой объект внутри, независимо от местоположения объекта внутри оболочки.

Следствием этого является то, что внутри твердой сферы постоянной плотности гравитационная сила внутри объекта изменяется линейно с расстоянием от центр, становящийся нулевым из-за симметрии в центре массы. Это можно увидеть следующим образом: возьмите точку внутри такой сферы на расстоянии $r\; \{\backslash \; displaystyle\; r\}$от центра сферы. Тогда вы можете игнорировать все оболочки большего радиуса, согласно теореме об оболочках. Таким образом, оставшаяся масса $m\; \{\backslash \; displaystyle\; m\}$пропорциональна $r\; 3\; \{\backslash \; displaystyle\; r\; ^\; \{3\}\}$(потому что она основана на объеме), а сила гравитации, действующая на него, пропорциональна $mr\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{m\}\; \{r\; ^\; \{2\}\}\}\}$(закон обратных квадратов ), поэтому общий гравитационный эффект пропорционален $r\; 3\; r\; 2\; =\; r\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{r\; ^\; \{3\}\}\; \{r\; ^\; \{2\}\}\}\; =\; r\}$, поэтому линейно в $r\; \{\backslash \; displaystyle\; r\}$.

Эти результаты были важны для ньютоновского анализа движения планет; они не очевидны сразу, но могут быть доказаны с помощью исчисления. (В качестве альтернативы, закон Гаусса для гравитации предлагает гораздо более простой способ доказать те же результаты.)

В дополнение к гравитации теорема оболочек также может быть использована для описывают электрическое поле, генерируемое статической сферически-симметричной плотностью заряда, или аналогично для любого другого явления, которое следует закону обратных квадратов. Приведенные ниже выводы сосредоточены на гравитации, но результаты могут быть легко обобщены на электростатическую силу.

• 1 Получение гравитационного поля вне твердой сферы
• 2 Вне оболочки
• 3 Внутри оболочка
• 4 Вывод с использованием закона Гаусса
• 5 Конверсии и обобщения
• 6 Доказательства Ньютона
  • 6.1 Введение
  • 6.2 Сила, действующая на точку внутри полой сферы
  • 6.3 Сила, действующая на точку вне полая сфера
• 7 Теорема оболочек в общей теории относительности
• 8 См. также
• 9 Ссылки

Есть три шага к доказательству теоремы Ньютона об оболочке. Сначала будет выведено уравнение для гравитационного поля, обусловленного кольцом масс. Собирая бесконечное количество бесконечно тонких колец для создания диска, это уравнение, включающее кольцо, будет использоваться для нахождения гравитационного поля, создаваемого диском. Наконец, собрав бесконечное количество бесконечно тонких дисков в сферу, это уравнение, включающее диск, будет использоваться для нахождения гравитационного поля, создаваемого сферой.

Гравитационное поле $E\; \{\backslash \; displaystyle\; E\}$в позиции с названием $P\; \{\backslash \; displaystyle\; P\}$в $(x,\; y)\; =\; (-\; p,\; 0)\; \{\backslash \; displaystyle\; (x,\; y)\; =\; (-\; p,\; 0)\}$на оси x из-за точки массы $M\; \{\backslash \; displaystyle\; M\; \}$в начале координат

$E\; point\; =\; GM\; p\; 2\; \{\backslash \; displaystyle\; E\_\; \{point\}\; =\; \{\backslash \; frac\; \{GM\}\; \{p\; ^\; \{2\}\}\}\}$

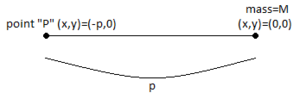
Предположим, что эта масса перемещается вверх по оси Y до точки $(0,\; R)\; \{\backslash \; displaystyle\; (0,\; R)\}$. Расстояние между $P\; \{\backslash \; displaystyle\; P\}$и массой точки теперь больше, чем раньше; Он становится гипотенузой прямоугольного треугольника с катетами $p\; \{\backslash \; displaystyle\; p\}$и $R\; \{\backslash \; displaystyle\; R\}$, что равно $p\; 2\; +\; R\; 2\; \{\backslash \; textstyle\; \{\backslash \; sqrt\; \{p\; ^\; \{2\}\; +\; R\; ^\; \{2\}\}\}\}$. Следовательно, гравитационное поле возвышенной точки:

$E\; elevatedpoint\; =\; GM\; p\; 2\; +\; R\; 2\; \{\backslash \; displaystyle\; E\_\; \{elevatedpoint\}\; =\; \{\backslash \; frac\; \{GM\}\; \{p\; ^\; \{2\}\; +\; R\; ^\; \{2\}\}\; \}\}$

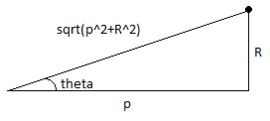
Величина гравитационного поля, которое притягивает частицу в точке $P\; \{\backslash \; displaystyle\; P\}$в направлении x, представляет собой гравитационное поле, умноженное на $cos\; \; (\; \theta )\; \{\backslash \; displaystyle\; \backslash \; cos\; (\backslash \; theta)\}$, где $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$- угол, примыкающий к оси x. В этом случае $cos\; \; (\theta )\; =\; pp\; 2\; +\; R\; 2\; \{\backslash \; displaystyle\; \backslash \; cos\; (\backslash \; theta)\; =\; \{\backslash \; frac\; \{p\}\; \{\backslash \; sqrt\; \{p\; ^\; \{2\}\; +\; R\; ^\; \{2\}\}\; \}\}\}$. Следовательно, величина гравитационного поля в направлении x, $E\; x\; \{\backslash \; displaystyle\; E\_\; \{x\}\}$равна:

$E\; x\; =\; GM\; cos\; \; \theta \; p\; 2\; +\; R\; 2\; \{\backslash \; displaystyle\; E\_\; \{x\}\; =\; \{\backslash \; frac\; \{GM\; \backslash \; cos\; \{\backslash \; theta\}\}\; \{p\; ^\; \{2\}\; +\; R\; ^\; \{2\}\}\}\}$

Подставляем в $cos\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; cos\; (\backslash \; theta)\}$дает

$E\; x\; =\; GM\; p\; (p\; 2\; +\; R\; 2)\; 3\; 2\; \{\backslash \; displaystyle\; E\_\; \{x\}\; =\; \{\backslash \; frac\; \{GMp\}\; \{(p\; ^\; \{2\}\; +\; R\; ^\; \{2\})\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\}\}$

Предположим, что эта масса равномерно распределена в кольце с центром в начале координат и обращенным к точке $P\; \{\backslash \; displaystyle\; P\}$с тем же радиусом $R\; \{\backslash \; displaystyle\; R\}$. Поскольку вся масса расположена под одним углом по отношению к оси x, а расстояние между точками на кольце такое же, как и раньше, гравитационное поле в направлении x в точке $P\; \{\; \backslash \; displaystyle\; P\}$из-за кольца совпадает с точечной массой, расположенной в точке $R\; \{\backslash \; displaystyle\; R\}$единиц выше оси y:

$E\; кольцо\; =\; GM\; p\; (p\; 2\; +\; R\; 2)\; 3\; 2\; \{\backslash \; displaystyle\; E\_\; \{ring\}\; =\; \{\backslash \; frac\; \{GMp\}\; \{(p\; ^\; \{2\}\; +\; R\; ^\; \{2\})\; ^\; \{\backslash \; frac\; \{3\}\; \{\; 2\}\}\}\}\}$

Чтобы найти гравитационное поле в точке $P\; \{\backslash \; displaystyle\; P\}$, создаваемое диском, бесконечное количество бесконечно тонких колец, обращенных к $P\; \{\backslash \; displaystyle\; P\}$, каждый с радиусом $y\; \{\backslash \; displaystyle\; y\}$, шириной $dy\; \{\backslash \; displaystyle\; dy\}$и массой of $d\; M\; \{\backslash \; displaystyle\; dM\}$могут быть помещены друг в друга для образования диска. Масса любого из колец $d\; M\; \{\backslash \; displaystyle\; dM\}$- это масса диска, умноженная на отношение площади кольца $2\; \pi \; ydy\; \{\backslash \; displaystyle\; 2\; \backslash \; pi\; y\; \backslash ,\; dy\}$к общей площади диска $\pi \; R\; 2\; \{\backslash \; displaystyle\; \backslash \; pi\; R\; ^\; \{2\}\}$. Итак, $d\; M\; =\; M\; \cdot \; 2\; y\; d\; y\; R\; 2\; \{\backslash \; displaystyle\; dM\; =\; \{\backslash \; frac\; \{M\; \backslash \; cdot\; 2y\; \backslash ,\; dy\}\; \{R\; ^\; \{2\}\}\}\}$. Следовательно, небольшое изменение гравитационного поля, $E\; \{\backslash \; displaystyle\; E\}$равно:

$d\; E\; =\; G\; pd\; M\; (p\; 2\; +\; y\; 2)\; 3\; 2\; \{\backslash \; displaystyle\; dE\; =\; \{\backslash \; frac\; \{Gp\; \backslash \; dM\}\; \{(p\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\}\}$

Подстановка в $d\; M\; \{\backslash \; displaystyle\; dM\; \}$и интегрирование обеих сторон дает гравитационное поле диска:

$E\; =\; \int \; GM\; p\; \cdot \; 2\; ydy\; R\; 2\; (p\; 2\; +\; y\; 2)\; 3\; 2\; \{\backslash \; displaystyle\; E\; =\; \backslash \; int\; \{\backslash \; гидроразрыв\; \{GMp\; \backslash \; \backslash \; cdot\; \{\backslash \; frac\; \{2y\; \backslash \; dy\}\; \{R\; ^\; \{2\}\}\}\}\; \{(p\; ^\; \{2\}\; +\; y\; ^\; \{2\})\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}\}\; \}$

Суммирование вклада в гравитационное поле от каждого из этих колец даст выражение для гравитационного поля, создаваемого диском. Это эквивалентно интегрированию указанного выше выражения от $y\; =\; 0\; \{\backslash \; displaystyle\; y\; =\; 0\}$до $y\; =\; R\; \{\backslash \; displaystyle\; y\; =\; R\}$, в результате чего в:

$E\; disc\; =\; 2\; GMR\; 2\; (1\; -\; pp\; 2\; +\; R\; 2)\; \{\backslash \; displaystyle\; E\_\; \{disc\}\; =\; \{\backslash \; frac\; \{2GM\}\; \{R\; ^\; \{2\}\}\}\; (1\; -\; \{\backslash \; frac\; \{p\; \}\; \{\backslash \; sqrt\; \{p\; ^\; \{2\}\; +\; R\; ^\; \{2\}\}\}\})\}$

Чтобы найти гравитационное поле в точке $P\; \{\backslash \; displaystyle\; P\}$, создаваемое сферой с центром в начале координат, бесконечное количество бесконечно тонких дисков, обращенных к $P\; \{\backslash \; displaystyle\; P\}$, каждый с радиусом $R\; \{\backslash \; displaystyle\; R\}$, шириной $dx\; \{\backslash \; displaystyle\; dx\}$и масса $d\; M\; \{\backslash \; displaystyle\; dM\}$могут быть помещены вместе.

Радиусы этих дисков $R\; \{\backslash \; displaystyle\; R\}$соответствуют высоте поперечного сечения сферы (с постоянным радиусом "$a\; \{\backslash \; displaystyle\; a\}$"), который представляет собой уравнение полукруга: $R\; =\; a\; 2\; -\; x\; 2\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -x\; ^\; \{2\}\}\}\}$. $x\; \{\backslash \; displaystyle\; x\}$варьируется от $-\; a\; \{\backslash \; displaystyle\; -a\}$до $a\; \{\backslash \; displaystyle\; a\}$.

Масса любой из дисков $d\; M\; \{\backslash \; displaystyle\; dM\}$- масса сферы $M\; \{\backslash \; displaystyle\; M\}$, умноженная на отношение объема бесконечно тонкий диск, деленный на объем сферы (с постоянным радиусом $a\; \{\backslash \; displaystyle\; a\}$). Объем бесконечно тонкого диска равен $\pi \; R\; 2\; dx\; \{\backslash \; displaystyle\; \backslash \; pi\; R\; ^\; \{2\}\; \backslash \; dx\}$или $\pi \; (a\; 2\; -\; x\; 2)\; dx\; \{\backslash \; displaystyle\; \backslash \; pi\; (a\; ^\; \{2\}\; -x\; ^\; \{2\})\; \backslash \; dx\}$. Итак, $d\; M\; =\; \pi \; M\; (a\; 2\; -\; x\; 2)\; dx\; 4\; 3\; \pi \; a\; 3\; \{\backslash \; displaystyle\; dM\; =\; \{\backslash \; frac\; \{\backslash \; pi\; M\; (a\; ^\; \{2\}\; -x\; ^\; \{2\})\; \backslash \; dx\; \}\; \{\{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash \; pi\; a\; ^\; \{3\}\}\}\}$. Упрощение дает $d\; M\; =\; 3\; M\; (a\; 2\; -\; x\; 2)\; dx\; 4\; a\; 3\; \{\backslash \; displaystyle\; dM\; =\; \{\backslash \; frac\; \{3M\; (a\; ^\; \{2\}\; -x\; ^\; \{2\})\; \backslash \; dx\}\; \{4a\; ^\; \{3\}\}\}\}$. Опять же, $x\; \{\backslash \; displaystyle\; x\}$изменяется от $-\; a\; \{\backslash \; displaystyle\; -a\}$до $a\; \{\backslash \; displaystyle\; a\}$.

Каждый положение дисков вдали от $P\; \{\backslash \; displaystyle\; P\}$будет варьироваться в зависимости от его положения в «сфере», состоящей из дисков, поэтому $p\; \{\backslash \; displaystyle\; p\}$необходимо заменить на $p\; +\; x\; \{\backslash \; displaystyle\; p\; +\; x\}$. $x\; \{\backslash \; displaystyle\; x\}$по-прежнему изменяется от $-\; a\; \{\backslash \; displaystyle\; -a\}$- $a\; \{\backslash \; displaystyle\; a\}$.

.

Замена $M\; \{\backslash \; displaystyle\; M\}$на $d\; M\; \{\backslash \; displaystyle\; dM\}$, $R\; \{\backslash \; displaystyle\; R\}$с $a\; 2\; -\; x\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -x\; ^\; \{2\}\}\}\}$и $p\; \{\backslash \; displaystyle\; p\}$с $p\; +\; x\; \{\backslash \; displaystyle\; p\; +\; x\}$в уравнении «диска» дает:

$d\; E\; =\; 2\; G\; [3\; M\; (a\; 2\; -\; x\; 2)]\; 4\; a\; 3\; (a\; 2\; -\; x\; 2)\; 2\; \cdot \; (1\; -\; p\; +\; x\; (p\; +\; x)\; 2\; +\; (a\; 2\; -\; x\; 2)\; 2)\; dx\; \{\backslash \; displaystyle\; dE\; =\; \{\backslash \; frac\; \{\backslash \; frac\; \{2G\; [3M\; (a\; ^\; \{2\}\; -x\; ^\; \{2\})]\}\; \{4a\; ^\; \{3\}\}\}\; \{(\{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -x\; ^\; \{2\}\}\})\; ^\; \{2\}\}\}\; \backslash \; cdot\; (1\; -\; \{\backslash \; frac\; \{p\; +\; x\}\; \{\backslash \; sqrt\; \{(p\; +\; x)\; ^\; \{2\}\; +\; (\{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -x\; ^\; \{2\}\}\})\; ^\; \{2\}\}\}\})\; \backslash \; dx\}$

Упрощение,

$\int \; d\; E\; =\; \int \; -\; aa\; 3\; GM\; 2\; a\; 3\; (1\; -\; p\; +\; xp\; 2\; +\; a\; 2\; +\; 2\; px)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; dE\; =\; \backslash \; int\; \_\; \{-\; a\}\; ^\; \{a\}\; \{\backslash \; frac\; \{3GM\}\; \{2a\; ^\; \{3\}\}\}\; (1\; -\; \{\backslash \; frac\; \{p\; +\; x\}\; \{\backslash \; sqrt\; \{p\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; +\; 2px\}\}\})\; \backslash \; dx\}$

Интегрирование гравитационного поля каждого тонкого диска от $x\; =\; -\; a\; \{\backslash \; displaystyle\; x\; =\; -a\}$до $x\; =\; +\; a\; \{\backslash \; displaystyle\; x\; =\; +\; a\}$с учетом на $x\; \{\backslash \; displaystyle\; x\}$, и, проделав некоторую осторожную алгебру, прекрасно дает теорему Ньютона об оболочке:

$E\; =\; GM\; p\; 2\; \{\backslash \; displaystyle\; E\; =\; \{\backslash \; frac\; \{GM\}\; \{p\; ^\; \{2\}\}\}\}$

где $p\; \{\backslash \; displaystyle\; p\}$- это расстояние между центром сферической массы и произвольной точкой $P\; \{\backslash \; displaystyle\; P\}$. Гравитационное поле сферической массы можно рассчитать, рассматривая всю массу как точечную частицу в центре сферы.

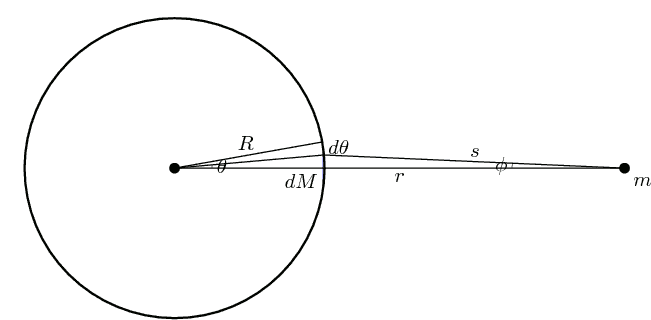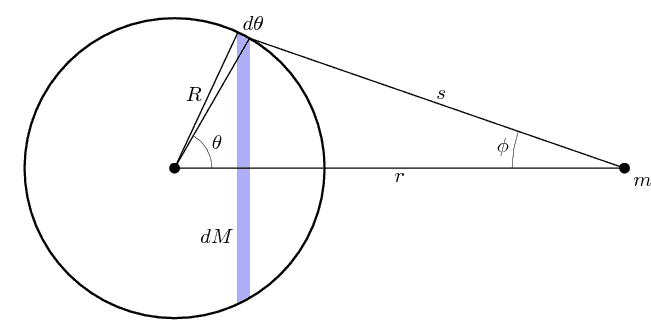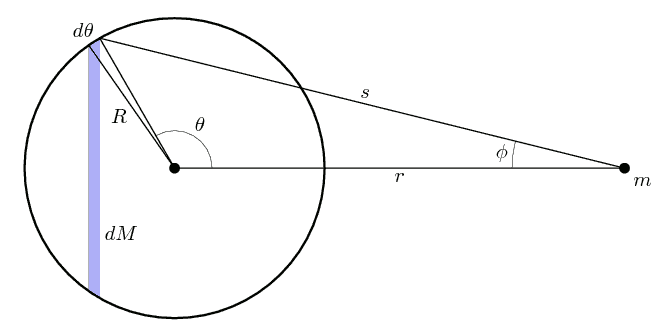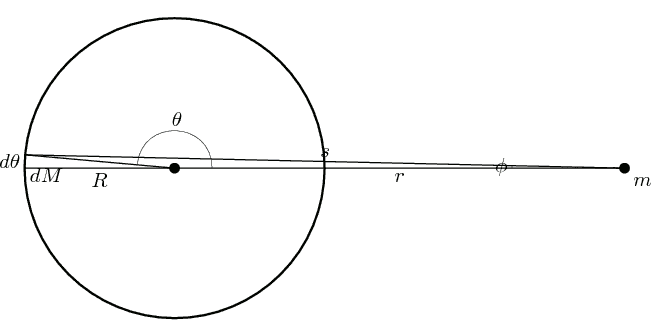
Твердое, сферически симметричное тело может быть смоделировано как бесконечное число концентрических бесконечно малых размеров. тонкие сферические оболочки. Если одну из этих оболочек можно рассматривать как точечную массу, то систему оболочек (то есть сферу) также можно рассматривать как точечную массу. Рассмотрим одну такую ​​оболочку (на схеме показано поперечное сечение):

(Примечание: $d\; \theta \; \{\backslash \; displaystyle\; d\; \backslash \; theta\}$на диаграмме относится к малому углу, а не к длина дуги. Длина дуги составляет $R\; d\; \theta \; \{\backslash \; textstyle\; R\; \backslash \; d\; \backslash \; theta\}$.)

Применение Универсального закона Ньютона Гравитация, сумма сил, создаваемых элементами массы в заштрихованной полосе, равна

$d\; F\; =\; G\; md\; M\; s\; 2\; \{\backslash \; displaystyle\; dF\; =\; \{\backslash \; frac\; \{Gm\; \backslash ;\; dM\}\; \{s\; ^\; \{2\; \}\}\}\}$

Однако, поскольку существует частичная компенсация из-за векторной природы силы в сочетании с симметрией круговой ленты, оставшаяся составляющая (в направлении, указывающем в направлении $m\; \{\backslash \; displaystyle\; m\}$) задается как

$d\; F\; r\; =\; G\; md\; M\; s\; 2\; cos\; \; \varphi \; \{\backslash \; displaystyle\; dF\_\; \{r\}\; =\; \{\backslash \; frac\; \{Gm\; \backslash ;\; dM\}\; \{s\; ^\; \{2\}\}\}\; \backslash \; cos\; \backslash \; phi\}$

Таким образом, общая сила, действующая на $m\; \{\backslash \; displaystyle\; m\}$, представляет собой просто сумму сил, прилагаемых всеми полосы. Уменьшая ширину каждой полосы и увеличивая количество полос, сумма становится интегральным выражением:

$F\; r\; =\; \int \; d\; F\; r\; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; \backslash \; int\; dF\_\; \{r\}\}$

Поскольку $G\; \{\backslash \; displaystyle\; G\}$и $m\; \{\backslash \; displaystyle\; m\}$являются константами, их можно вынести из интеграла:

$F\; r\; =\; G\; m\; \int \; cos\; \; \varphi \; d\; M\; s\; 2.\; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; Gm\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; cos\; \backslash \; phi\; \backslash \; dM\}\; \{s\; ^\; \{2\}\}\}.\}$

Чтобы вычислить этот интеграл, нужно сначала выразить $d\; M\; \{\; \backslash \; displaystyle\; dM\}$как функция от $d\; \theta \; \{\backslash \; displaystyle\; d\; \backslash \; theta\}$

Общая поверхность сферической оболочки составляет

$4\; \pi \; R\; 2\; \{\backslash \; displaystyle\; 4\; \backslash \; pi\; R\; ^\; \{2\}\}$

, а площадь поверхности тонкого среза между $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$и $\theta \; +\; d\; \theta \; \{\backslash \; displaystyle\; \backslash \; theta\; +\; d\; \backslash \; theta\}$is

$2\; \pi \; R\; грех\; \; \theta \; \cdot \; R\; d\; \theta \; =\; 2\; \pi \; R\; 2\; sin\; \; \theta \; d\; \theta \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\; R\; \backslash \; sin\; \backslash \; theta\; \backslash \; cdot\; R\; \backslash ,\; d\; \backslash \; theta\; =\; 2\; \backslash \; pi\; R\; ^\; \{2\}\; \backslash \; sin\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\}$

Если масса снаряда $M\; \{\backslash \; displaystyle\; M\}$, значит,

$d\; M\; =\; 2\; \pi \; R\; 2\; грех\; \; \theta \; 4\; \pi \; R\; 2\; M\; d\; \theta \; =\; 1\; 2\; M\; sin\; \; \theta \; d\; \theta \; \{\backslash \; displaystyle\; dM\; =\; \{\backslash \; frac\; \{2\; \backslash \; pi\; R\; ^\; \{2\}\; \backslash \; sin\; \backslash \; theta\}\; \{4\; \backslash \; pi\; R\; ^\; \{2\}\}\}\; M\; \backslash ,\; d\; \backslash \; theta\; =\; \backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; M\; \backslash \; sin\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\}$

и

$F\; r\; =\; GM\; m\; 2\; \int \; sin\; \; \theta \; соз\; \; \varphi \; s\; 2\; d\; \theta \; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; \{\backslash \; frac\; \{GMm\}\; \{2\}\}\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; sin\; \backslash \; theta\; \backslash \; cos\; \backslash \; phi\}\; \{s\; ^\; \{2\}\}\}\; \backslash ,\; d\; \backslash \; theta\}$

По закону косинусов ,

$cos\; \; \varphi \; =\; r\; 2\; +\; s\; 2\; -\; R\; 2\; 2\; rs\; \{\backslash \; displaystyle\; \backslash \; cos\; \backslash \; phi\; =\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; +\; s\; ^\; \{2\}\; -R\; ^\; \{2\}\}\; \{2rs\}\}\}$

и

$cos\; \; \theta \; =\; r\; 2\; +\; R\; 2\; -\; s\; 2\; 2\; r\; R.\; \{\backslash \; displaystyle\; \backslash \; cos\; \backslash \; theta\; =\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; +\; R\; ^\; \{2\}\; -s\; ^\; \{2\}\}\; \{2rR\}\}.\}$

Эти два отношения связывают три параметра $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$и $s\; \{\backslash \; displaystyle\; s\}$, которые вместе входят в интеграл. Поскольку $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$увеличивается с $0\; \{\backslash \; displaystyle\; 0\}$до $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$радианы, $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$изменяется от начального значения 0 до максимального значения, прежде чем окончательно вернуться к нулю при $\theta \; =\; \pi \; \{\backslash \; displaystyle\; \backslash \; theta\; =\; \backslash \; pi\}$. В то же время $s\; \{\backslash \; displaystyle\; s\}$увеличивается от начального значения $r\; -\; R\; \{\backslash \; displaystyle\; rR\}$до конечного значения $r\; +\; R\; \{\backslash \; displaystyle\; r\; +\; R\}$как $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$увеличивается с 0 до $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$радианы. Это показано на следующей анимации:

(Примечание: если смотреть с $m\; \{\backslash \; displaystyle\; m\}$, заштрихованная синяя полоса выглядит как тонкое кольцо, внутреннее и внешние радиусы сходятся к $R\; sin\; \; \theta \; \{\backslash \; displaystyle\; R\; \backslash \; \backslash \; sin\; \backslash \; theta\}$, поскольку $d\; \theta \; \{\backslash \; displaystyle\; d\; \backslash \; theta\}$исчезает.)

Чтобы найти примитивную функцию подынтегральной функции, нужно сделать $s\; \{\backslash \; displaystyle\; s\}$независимой переменной интегрирования вместо $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$.

Выполнение неявного дифференцирования второго из приведенных выше выражений "закона косинуса" дает

$-\; sin\; \; \theta \; d\; \theta \; =\; -\; 2\; s\; 2\; r\; R\; ds\; \{\backslash \; displaystyle\; -\; \backslash \; sin\; \backslash \; theta\; \backslash ;\; d\; \backslash \; theta\; =\; \{\backslash \; frac\; \{-2s\}\; \{2rR\}\}\; ds\}$

и, следовательно,

$sin\; \; \theta \; d\; \theta \; =\; sr\; R\; ds.\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; theta\; \backslash ;\; d\; \backslash \; theta\; =\; \{\backslash \; frac\; \{s\}\; \{rR\}\}\; ds.\}$

Отсюда следует, что

$F\; r\; =\; GM\; m\; 2\; 1\; r\; R\; \int \; s\; cos\; \; \varphi \; s\; 2\; ds\; знак\; равно\; GM\; м\; 2\; р\; р\; \int \; соз\; \; \varphi \; sds\; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; \{\backslash \; frac\; \{GMm\}\; \{2\}\}\; \{\backslash \; frac\; \{1\}\; \{rR\}\}\; \backslash \; int\; \{\backslash \; frac\; \{s\; \backslash \; cos\; \backslash \; phi\}\; \{s\; ^\; \{2\}\}\}\; \backslash ,\; ds\; =\; \{\backslash \; frac\; \{GMm\}\; \{2rR\}\}\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; cos\; \backslash \; phi\}\; \{s\}\}\; \backslash ,\; ds\}$

где новый переменная интегрирования $s\; \{\backslash \; displaystyle\; s\}$увеличивается с $r\; -\; R\; \{\backslash \; displaystyle\; rR\}$до $r\; +\; R\; \{\backslash \; displaystyle\; r\; +\; R\}$.

Вставив выражение для $cos\; \; \varphi \; \{\backslash \; displaystyle\; \backslash \; cos\; \backslash \; phi\}$с использованием первого из приведенных выше выражений «закона косинуса», мы наконец получаем, что

$F\; r\; =\; GM\; м\; 4\; р\; 2\; R\; \int \; (1\; +\; r\; 2\; -\; R\; 2\; s\; 2)\; дс.\; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; \{\backslash \; frac\; \{GMm\}\; \{4r\; ^\; \{2\}\; R\}\}\; \backslash \; int\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; -R\; ^\; \{2\}\}\; \{s\; ^\; \{\; 2\}\}\}\; \backslash \; right)\; \backslash \; ds\; \backslash .\}$

A примитивная функция для подынтегрального выражения

$s\; -\; r\; 2\; -\; R\; 2\; s,\; \{\backslash \; displaystyle\; s\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; -R\; ^\; \{2\}\}\; \{s\}\}\; \backslash ,\}$

и вставка границ $r\; -\; R\; \{\backslash \; displaystyle\; rR\}$и $r\; +\; R\; \{\backslash \; displaystyle\; r\; +\; R\}$для переменной интегрирования $s\; \{\backslash \; displaystyle\; s\}$в этой примитивной функции получается, что

$F\; r\; =\; GM\; mr\; 2\; \{\backslash \; displaystyle\; F\_\; \{r\; \}\; =\; \{\backslash \; frac\; \{GMm\}\; \{r\; ^\; \{2\}\}\}\}$,

говоря, что гравитационная сила такая же, как у точечной массы в центре оболочки с такой же массой.

Наконец, объедините всю бесконечно тонкую сферическую оболочку с массой $d\; M\; \{\backslash \; displaystyle\; dM\}$, и мы сможем получить общий гравитационный вклад твердого шара в объект снаружи мяч

$F\; total\; =\; \int \; d\; F\; r\; =\; G\; mr\; 2\; \int \; d\; M.\; \{\backslash \; displaystyle\; F\_\; \{total\}\; =\; \backslash \; int\; dF\_\; \{r\}\; =\; \{\backslash \; frac\; \{Gm\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; int\; dM.\}$

Между радиусом $x\; \{\backslash \; displaystyle\; x\}$- $x\; +\; dx\; \{\backslash \; displaystyle\; x\; +\; dx\}$, $d\; M\; \{\backslash \; displaystyle\; dM\}$может быть выражено как функция от $x\; \{\backslash \; displaystyle\; x\}$, т. е.

$d\; M\; =\; 4\; \pi \; x\; 2\; dx\; 4\; 3\; \pi \; R\; 3\; M\; =\; 3\; M\; x\; 2\; dx\; R\; 3\; \{\backslash \; displaystyle\; dM\; =\; \{\backslash \; frac\; \{4\; \backslash \; pi\; x\; ^\; \{2\}\; dx\}\; \{\{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash \; pi\; R\; ^\; \{3\}\}\}\; M\; =\; \{\backslash \; frac\; \{3Mx\; ^\; \{2\}\; dx\}\; \{R\; ^\; \{3\}\}\}\}$

Следовательно, общая гравитация

$F\; total\; =\; 3\; GM\; mr\; 2\; R\; 3\; \int \; 0\; R\; x\; 2\; dx\; =\; GM\; mr\; 2\; \{\backslash \; displaystyle\; F\_\; \{total\}\; =\; \{\backslash \; frac\; \{3GMm\}\; \{r\; ^\; \{2\}\; R\; ^\; \{3\}\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{R\}\; x\; ^\; \{2\}\; dx\; =\; \{\backslash \; frac\; \{GMm\}\; \{r\; ^\; \{2\}\}\}\}$

, что предполагает, что сила тяжести твердого сферического шара к внешнему объекту можно упростить как точечную массу в центре шара с той же массой.

Для точки внутри оболочки разница заключается в том, что, когда θ равно нулю, ϕ принимает значение π радиан, а s - значение R - r. Когда θ увеличивается от 0 до π радиан, ϕ уменьшается от начального значения π радиан до нуля, а s увеличивается от начального значения R - r до значения R + r.

Все это можно увидеть на следующем рисунке

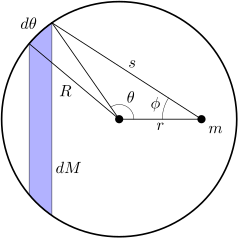
Вставка этих границ в примитивную функцию

$s\; -\; r\; 2\; -\; R\; 2\; s\; \{\backslash \; displaystyle\; s\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; -R\; ^\; \{2\}\}\; \{s\}\}\}$

получается, что в данном случае

$F\; r\; =\; 0,\; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; 0\; \backslash ,\}$

говоря, что чистые гравитационные силы, действующие на точечную массу со стороны элементов массы оболочки за пределами точки измерения, компенсируются.

Обобщение: Если $f\; =\; krp\; \{\backslash \; displaystyle\; f\; =\; \{\backslash \; frac\; \{k\}\; \{r\; ^\; \{p\}\}\}\}$, результирующая сила внутри оболочки равна:

$F\; (r)\; =\; GM\; m\; 4\; r\; 2\; R\; \int \; R\; -\; r\; R\; +\; r\; (1\; sp\; -\; 2\; +\; r\; 2\; -\; R\; 2\; sp)\; ds\; \{\backslash \; displaystyle\; F\; (r)\; =\; \{\backslash \; frac\; \{GMm\}\; \{\; 4r\; ^\; \{2\}\; R\}\}\; \backslash \; int\; \_\; \{Rr\}\; ^\; \{R\; +\; r\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{s\; ^\; \{p-2\}\}\}\; +\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; -\; R\; ^\; \{2\}\}\; \{s\; ^\; \{p\}\}\}\; \backslash \; right)\; \backslash ,\; ds\}$

Результатом выше является $F\; (r)\; \{\backslash \; displaystyle\; F\; (r)\}$идентично нулю тогда и только тогда, когда $p\; =\; 2\; \{\backslash \; displaystyle\; p\; =\; 2\}$

вне оболочки (т.е. $r>R\; \{\backslash \; displaystyle\; r>R\}$или ):

$F\; (\; г)\; знак\; равно\; GM\; м\; 4\; р\; 2\; р\; \int \; р\; -\; р\; р\; +\; R\; (1\; sp\; -\; 2\; +\; r\; 2\; -\; R\; 2\; sp)\; ds\; \{\backslash \; displaystyle\; F\; (r)\; =\; \{\backslash \; frac\; \{GMm\}\; \{4r\; ^\; \{2\}\; R\}\}\; \backslash \; int\; \_\; \{rR\}\; ^\; \{r\; +\; R\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{s\; ^\; \{p-2\}\}\}\; +\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; -R\; ^\; \{2\})\; \}\; \{s\; ^\; \{p\}\}\}\; \backslash \; right)\; \backslash ,\; ds\}$

Теорема оболочек является непосредственным следствием f закон Гаусса для гравитации, согласно которому

$\int \; S\; g\; \cdot \; d\; S\; =\; -\; 4\; \pi \; GM\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{S\}\; \{\backslash \; mathbf\; \{g\}\}\; \backslash \; cdot\; \backslash ,\; d\; \{\backslash \; mathbf\; \{S\}\}\; =\; -\; 4\; \backslash \; pi\; GM\}$

где M - масса части сферически-симметричного распределения массы, которая находится внутри сферы с радиусом r, и

$\int \; S\; g\; \cdot \; d\; S\; =\; \int \; S\; г\; \cdot \; N\; ^\; d\; S\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{S\}\; \{\backslash \; mathbf\; \{g\}\}\; \backslash \; cdot\; \backslash ,\; d\; \{\backslash \; mathbf\; \{S\}\}\; =\; \backslash \; int\; \_\; \{S\}\; \{\backslash \; mathbf\; \{g\}\}\; \backslash \; cdot\; \{\backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}\; \backslash ,\; dS\}$

- это поверхностный интеграл гравитационного поля gнад любой замкнутой поверхностью, внутри которой общая масса равна M, единичный вектор $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$, являющийся внешней нормалью к поверхности.

Гравитационное поле сферически-симметричного распределения массы, такого как материальная точка, сферическая оболочка или однородная сфера, также должно быть сферически симметричным. Если $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$является единичным вектором в направлении от точки симметрии к другой точке, гравитационное поле в этой другой точке должно быть

$g\; =\; g\; (r)\; n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{g\}\; =\; g\; (r)\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$

где g (r) зависит только от расстояния r до точка симметрии

Выбор замкнутой поверхности как сферы с радиусом r с центром в точке симметрии, являющейся внешней нормалью к точке на поверхности, $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{\; n\}\}\}$, это в точности направление, указывающее от точки симметрии распределения массы.

Следовательно, у одного есть это

$g\; =\; g\; (r)\; n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{g\}\; =\; g\; (r)\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$

и

$\int \; S\; г\; \cdot \; d\; S\; знак\; равно\; г\; (г)\; \int \; S\; d\; S\; знак\; равно\; г\; (г)\; 4\; \pi \; р\; 2\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{S\}\; \backslash \; mathbf\; \{g\}\; \backslash \; cdot\; \backslash ,\; d\; \{\backslash \; mathbf\; \{\; S\}\}\; =\; g\; (r)\; \backslash \; int\; \_\; \{S\}\; \backslash ,\; d\; \{S\}\; =\; g\; (r)\; 4\; \backslash \; pi\; r\; ^\; \{2\}\}$

, поскольку площадь сферы равна 4πr.

Из закона Гаусса следует, что

$g\; (r)\; 4\; \pi \; r\; 2\; =\; -\; 4\; \pi \; GM\; \{\backslash \; displaystyle\; g\; (r)\; 4\; \backslash \; pi\; r\; ^\; \{2\}\; =\; -\; 4\; \backslash \; pi\; GM\; \}$

т.е. что

$g\; (r)\; =\; -\; G\; M\; r\; 2.\; \{\backslash \; displaystyle\; g\; (r)\; =\; -\; \{\backslash \; frac\; \{GM\}\; \{r\; ^\; \{2\}\}\}.\}$

Естественно спросить, обратится ли теоремы об оболочке верна, а именно, следует ли из результата теоремы закон всемирного тяготения, или существует более общий закон силы, для которого теорема верна. Более конкретно, можно задать вопрос:

Предположим, существует сила $F\; \{\backslash \; displaystyle\; F\}$между массами M и m, разделенными расстоянием r вида $F\; =\; M\; mf\; (r)\; \{\backslash \; displaystyle\; F\; =\; Mmf\; (r)\}$так, что любое сферически симметричное теловоздействует на внешние тела, как если бы его масса была сосредоточена в его центре. Тогда какую форму может принимать функцию $f\; \{\backslash \; displaystyle\; f\}$?

Фактически, это допускает ровно на один класс силы больше, чем (ньютоновский) обратный квадрат. Наиболее общая сила, полученная в:

$F\; =\; -\; GM\; mr\; 2\; -\; \Lambda \; M\; mr\; 3\; \{\backslash \; displaystyle\; F\; =\; -\; \{\backslash \; frac\; \{GMm\}\; \{r\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; Lambda\; Mmr\}\; \{3\}\}\}$

где $G\; \{\backslash \; displaystyle\; G\}$и $\Lambda \; \{\backslash \; displaystyle\; \backslash \; Lambda\}$могут быть константами, принимающими любое значение. Первый член - это всемирный законного тяготения; вторая - дополнительная сила, аналогичная члену космологическая постоянная в общей теории относительности.

Если мы дополнительно ограничим силу потребовав, чтобы вторая часть теоремы также выполнялась, а именно, что существует отсутствие силы внутри полого шара, мы исключаем возможность дополнительного члена, и закон обратных квадратов действительно является единственным силовым, удовлетворяющим теореме.

С другой стороны, если мы ослабим условия и потребуем только, чтобы поле везде за пределами сферически симметричного тела было таким же, как поле некоторой точечной массы в центре (любой массы), мы допускаем новый класс решений, задаваемый потенциалом Юкавы, частным случаем которого является закон обратных квадратов.

Другое обобщение можно сделать для диска, заметив, что

$d\; M\; =\; R\; 2\; 2\; d\; \theta \; sin\; 2\; \; \theta \; \pi \; R\; 2\; M\; =\; sin\; 2\; \; \theta \; 2\; \pi \; M\; d\; \theta \; \{\backslash \; displaystyle\; dM\; =\; \{\backslash \; frac\; \{R\; ^\; \{2\}\}\; \{2\}\}\; \{\backslash \; frac\; \{d\; \backslash \; theta\; \backslash \; sin\; ^\; \{2\}\; \{\backslash \; theta\}\}\; \{\backslash \; pi\; R\; ^\; \{2\}\}\}\; M\; =\; \{\backslash \; frac\; \{\backslash \; sin\; ^\; \{2\}\; \{\backslash \; theta\}\}\; \{2\; \backslash \; pi\}\}\; Md\; \backslash \; theta\}$

так:

$F\; r\; =\; GM\; m\; 2\; \pi \; \int \; sin\; 2\; \; \theta \; cos\; \; \varphi \; s\; 2\; d\; \theta ,\; \{\backslash \; displaystyle\; F\_\; \{r\}\; =\; \{\backslash \; frac\; \{GMm\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; sin\; ^\; \{2\}\; \{\backslash \; theta\}\; \backslash \; cos\; \backslash \; phi\}\; \{s\; ^\; \{2\}\}\}\; d\; \backslash \; theta,\; \}$

где $M\; =\; \pi \; R\; 2\; \rho \; \{\backslash \; displaystyle\; M\; =\; \backslash \; pi\; R\; ^\; \{2\}\; \backslash \; rho\}$и $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$- плотность тела.

Выполняя все промежуточные вычисления, получаем:

$F\; (r)\; =\; G\; m\; \rho \; 8\; r\; 3\; \int \; R\; -\; r\; R\; +\; r\; (r\; 2\; +\; s\; 2\; -\; R\; 2)\; 2\; (r\; 2\; R\; 2\; +\; r\; 2\; s\; 2\; +\; R\; 2\; s\; 2)\; -\; s\; 4\; -\; r\; 4\; -\; R\; 4\; s\; 2\; ds\; \{\backslash \; displaystyle\; F\; (r)\; =\; \{\backslash \; frac\; \{Gm\; \backslash \; rho\}\; \{8r\; ^\; \{3\}\}\}\; \backslash \; int\; \_\; \{Rr\}\; ^\; \{R\; +\; r\}\; \{\backslash \; frac\; \{(r\; ^\; \{2\}\; +\; s\; ^\; \{2\}\; -R\; ^\; \{2\})\; \{\backslash \; sqrt\; \{2\; (r\; ^\; \{2\}\; R\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; s\; ^\; \{2\}\; +\; R\; ^\; \{2\}\; s\; ^\; \{2\})\; -\; s\; ^\; \{4\}\; -r\; ^\; \{4\}\; -R\; ^\; \{4\}\}\}\}\; \{s\; ^\; \{2\}\}\}\; \backslash ,\; ds\}$

Введение

В предложениях 70 и 71 рассматривается сила, действующая на частицу со стороны полой поверхности с бесконечно тонкой поверхности, массовая плотность постоянной поверхности. Сила, действующая на частицу со стороны небольшого участка поверхности, пропорциональна массе этой области и обратно пропорциональна квадрату расстояния до частиц. Первое предложение рассматривает случай, когда часть находится внутри сферы, второе - когда она находится снаружи. Использование бесконечно малых и предельных процессов в геометрических конструкциях является простым и элегантным, вызывающим необходимость в каких-либо интеграциях. Они хорошо иллюстрируют метод Ньютона для доказательства положений «Начала».

Его доказательство предложения 70 тривиально. Далее он рассматривается немного более подробно, чем предоставлен Ньютон.

Доказательство предложения 71 более исторически значимо. Это составляет часть его доказательства, что гравитационная сила твердой сферы, действующей на ее пределами, обратно пропорциональна квадрату ее расстояния от центра сферы, при условии, что плотность в любой точке внутри сферы является функцией только на расстоянии от центра сферы.

Хотя нижеследующее полностью соответствует доказательствам Ньютона, были внесены очень незначительные изменения, чтобы попытаться сделать их более ясными.

Сила, действующая на точку внутри полой сферы

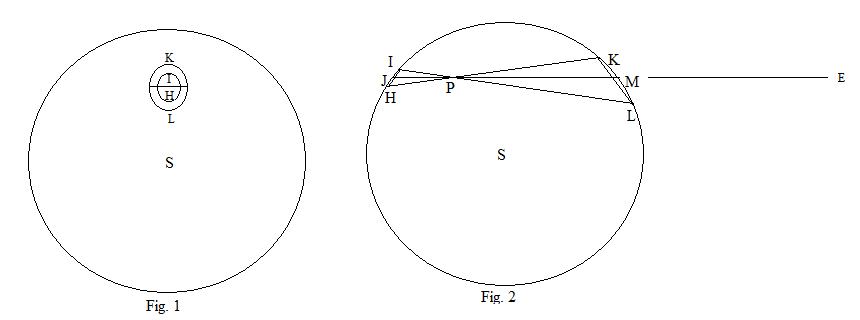
Рис. 2 - поперечное сечение полой сферы через центр S и произвольную точку P внутри сферы. Через P проведите две прямые IL и HK так, чтобы угол KPL был очень малым. JM - это линия, проходящая через P, которая делит этот угол пополам. По геометрии окружностей треугольники IPH и KPL похожи. Прямые KH и IL вращаются вокруг оси JM, образуя 2 конуса, которые пересекают сферу двумя замкнутыми кривыми. На рис. 1 сфера видна с расстояния по линии PE и считается прозрачной, поэтому видны обе кривые.

Поверхность сферы, которую пересекают конусы, можно считать плоской, и $\angle \; PJI\; =\; \angle \; PMK\; \{\backslash \; displaystyle\; \backslash \; angle\; PJI\; =\; \backslash \; angle\; PMK\}$.

Временное пересечение конус с плоскостью представляет собой эллипс, в В этом случае пересечения образуют два эллипса большими осями IH и KL, где $IHKL\; =\; PJPM\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{IH\}\; \{KL\}\}\; =\; \{\backslash \; frac\; \{PJ\}\; \{PM\}\}\}$.

По аналогичному второстепенные оси имеют одинаковое соотношение. Это ясно, если смотреть на с сверху сверху. Поэтому два эллипса похожи, поэтому их площади равны квадратам их главных осей. Масса любого участка изображения площади этого участка, для двух эллиптических областей соотношение масс $\propto \; PJ\; 2\; PM\; 2\; \{\backslash \; displaystyle\; \backslash \; propto\; \{\backslash \; frac\; \{PJ\; ^\; \{2\}\}\; \{PM\; ^\; \{2\}\}\}\}$.

Временная сила притяжения на P в JM из любого из эллиптического направления, как масса области, и обратно пропорциональна квадрату ее расстояния от P, он не зависит от расстояния P от сферы. Следовательно, силы на P от двух бесконечно малых эллиптических областей равны и противоположны, и в направлении JM нет результирующей силы.

положение P и направление JM произвольны, из этого следует, что любая часть внутри полой сферы не испытывает результирующей силы со стороны массы сферы.

Примечание: Ньютон просто приведены дуги IH и KL как «минимально малые», а области, очерченные линии IL и HK, могут иметь любую форму, не обязательно эллиптическую, но они всегда будут похожи.

Сила, действующая на точку вне полой сферы

Рис. 1 - поперечное сечение полой сферы через центр S с произвольной точкой P вне сферы. PT - это касательная к окружности в точке T, которая проходит через P. HI - это небольшая дуга на поверхности, такая что PH меньше PT. Растяните PI, чтобы пересечь сферу в L, и провести SF к точке F, которая делит IL пополам. Растяните PH, чтобы пересечь сферу в точку K, и проведите SE до точки E, которая пересекает HK пополам, и продолжите SF до пересечения HK в точке D. Опустите перпендикуляр IQ на линию PS, соединяющую точку P с центром S. - a, а расстояние PS - D.

Пусть дуга IH продолжается перпендикулярно плоскости диаграммы на небольшом расстоянии ζ. Площадь созданного рисунка равная $I\; H\; \cdot \; \zeta \; \{\backslash \; displaystyle\; IH\; \backslash \; cdot\; \backslash \; zeta\}$, а его масса пропорциональна этому продукту.

Сила, действующая на частицу этой массы в точке P $\propto \; IH\; \cdot \; \zeta \; PI\; 2\; \{\backslash \; displaystyle\; \backslash \; propto\; \{\backslash \; frac\; \{IH\; \backslash \; cdot\; \backslash \; zeta\}\; \{PI\; ^\; \{2\}\}\}\}$и находится вдоль линии PI.

Составляющая эту силу по направлению к центру $\propto \; IH\; \cdot \; PQ\; \cdot \; \zeta \; PI\; 3\; \{\backslash \; displaystyle\; \backslash \; propto\; \{\backslash \; frac\; \{IH\; \backslash \; cdot\; PQ\; \backslash \; cdot\; \backslash \; zeta\}\; \{PI\; ^\; \{3\}\}\}\; \}$.

Если теперь дуга HI полностью повернута вокруг линии PS, чтобы сформировать кольцо шириной HI и радиусом IQ, длина кольца равна 2π.IQ, а его площадь - 2π.IQ.IH. Составляющая силы этого кольца, действующая на частицу в точке P в направлении PS, становится $\propto \; IH\; \cdot \; IQ\; \cdot \; PQPI\; 3\; \{\backslash \; displaystyle\; \backslash \; propto\; \{\backslash \; frac\; \{IH\; \backslash \; cdot\; IQ\; \backslash \; cdot\; PQ\}\; \{PI\; ^\; \{3\}\}\; \}\}$.

Перпендикулярные компоненты силы, направленные к PS, компенсируются, поскольку масса в кольце распределяется симметрично относительно PS. Таким образом, составляющая в направлении PS представляет собой полную силу, действующую на P из-за кольца, образованного вращением дуги HI вокруг PS.

Из похожих треугольников: $IQPI\; =\; FSD\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{IQ\}\; \{PI\}\}\; =\; \{\backslash \; frac\; \{FS\}\; \{D\}\}\}$; $PQPI\; =\; PFD\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{PQ\}\; \{PI\}\}\; =\; \{\backslash \; frac\; \{PF\}\; \{D\}\}\}$и $RIPI\; =\; DFPF\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{RI\}\; \{PI\}\}\; =\; \{\; \backslash \; frac\; \{DF\}\; \{PF\}\}\}$

Если HI достаточно мало, чтобы его можно было принять за прямую линию, $\angle \; SIH\; \{\backslash \; displaystyle\; \backslash \; angle\; SIH\}$является правильным углом и $\angle \; RIH\; =\; \angle \; FIS\; \{\backslash \; displaystyle\; \backslash \; angle\; RIH\; =\; \backslash \; angle\; FIS\}$, так что $HIRI\; =\; IF\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{HI\}\; \{RI\}\}\; =\; \{\backslash \; frac\; \{a\}\; \{IF\}\}\}$.

Следовательно, сила, действующая на P из-за кольца $\propto \; IH\; \cdot \; IQ\; \cdot \; PQPI\; 3\; =\; a\; \cdot \; DF\; \cdot \; FS\; \cdot \; PFIF\; \cdot \; PF\; \cdot \; D\; \cdot \; D\; =\; a\; \cdot \; DF\; \cdot \; FSIF\; \cdot \; D\; 2\; \{\backslash \; displaystyle\; \backslash \; propto\; \{\backslash \; frac\; \{IH\; \backslash \; cdot\; IQ\; \backslash \; cdot\; PQ\}\; \{PI\; ^\; \{3\}\}\}\; =\; \{\backslash \; frac\; \{a\; \backslash \; cdot\; DF\; \backslash \; cdot\; FS\; \backslash \; cdot\; PF\}\; \{IF\; \backslash \; cdot\; PF\; \backslash \; cdot\; D\; \backslash \; cdot\; D\}\}\; =\; \{\backslash \; frac\; \{a\; \backslash \; cdot\; DF\; \backslash \; cdot\; FS\}\; \{IF\; \backslash \; cdot\; D\; ^\; \{2\}\}\}\}$.

Предположим, что на рис. 2 другая частица вне сферы в точке p, находящейся на расстоянии d от центра сферы re, с точками, написанными строчными буквами. Для удобства конструкции P на рис. 1 также на рис. 2. Как и раньше, тел. Меньше pt.

Создайте кольцо шириной ih и радиусом iq, сделав угол $fi\; S\; =\; FIS\; \{\backslash \; displaystyle\; fiS\; =\; FIS\}$и немного больший угол $dh\; S\; =\; DHS\; \{\backslash \; displaystyle\; dhS\; =\; DHS\}$, так что расстояние PS покрывается тем же углом в точке I, что и pS в точке i. То же самое верно для H и h соответственно.

Общая сила, действующая на p, создаваемая этим кольцом, составляет

$\propto \; ih\; \cdot \; iq\; \cdot \; pqpi\; 3\; =\; a\; \cdot \; df\; \cdot \; f\; S,\; если\; \cdot \; d\; 2\; \{\backslash \; displaystyle\; \backslash \; propto\; \{\backslash \; frac\; \{ih\; \backslash \; cdot\; iq\; \backslash \; cdot\; pq\}\; \{pi\; ^\; \{3\}\}\}\; =\; \{\backslash \; frac\; \{a\; \backslash \; cdot\; df\; \backslash \; cdot\; fS\}\; \{if\; \backslash \; cdot\; d\; ^\; \{2\}\}\}\}$

Очевидно, $f\; S\; =\; FS\; \{\backslash \; displaystyle\; fS\; =\; FS\}$, $if\; =\; IF\; \{\backslash \; displaystyle\; if\; =\; IF\}$и $e\; S\; =\; ES\; \{\backslash \; displaystyle\; eS\; =\; ES\}$.

Ньютон утверждает, что DF и df могут в пределе можно считать равными, поскольку углы DPF и dpf «обращаются в нуль вместе». Обратите внимание, что углы DPF и dpf не равны. Хотя DS и dS становятся равными в пределе, это не означает, что отношение DF к df становится равным единице, когда оба DF и df стремятся к нулю. В конечном случае DF зависит от D, а df - от d, поэтому они не равны.

Поскольку отношение DF к df в пределе имеет решающее значение, требуется более подробный анализ. Из аналогичных прямоугольных треугольников $DFPF\; =\; EDES\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{DF\}\; \{PF\}\}\; =\; \{\backslash \; frac\; \{ED\}\; \{ES\}\}\}$и $ED\; 2\; =\; (DF\; +\; FS)\; 2\; -\; ES\; 2\; \{\backslash \; displaystyle\; ED\; ^\; \{2\}\; =\; (DF\; +\; FS)\; ^\; \{2\}\; -ES\; ^\; \{2\}\}$, что дает $(PF\; 2\; -\; ES\; 2)\; DF\; 2\; PF\; 2\; +\; 2.\; FS.\; DF\; +\; FS\; 2\; -\; ES\; 2\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{(PF\; ^\; \{2\}\; -ES\; ^\; \{2\})\; DF\; ^\; \{2\}\}\; \{PF\; ^\; \{2\}\}\}\; +\; 2.FS.DF\; +\; FS\; ^\; \{2\}\; -ES\; ^\; \{2\}\; =\; 0\}$. Решение квадратичного для DF в пределе, когда ES приближается к FS, меньшему корню, $D\; F\; =\; E\; S\; -\; F\; S\; \{\backslash \; displaystyle\; DF\; =\; ES-FS\}$. Проще говоря, когда DF приближается к нулю, в пределе член $DF\; 2\; \{\backslash \; displaystyle\; DF\; ^\; \{2\}\}$можно игнорировать: $2\; \cdot \; FS\; \cdot \; DF\; +\; FS\; 2\; -\; ES\; 2\; =\; 0\; \{\backslash \; displaystyle\; 2\; \backslash \; cdot\; FS\; \backslash \; cdot\; DF\; +\; FS\; ^\; \{2\}\; -ES\; ^\; \{2\}\; =\; 0\}$, что приводит к тому же результату. Очевидно, что df имеет тот же предел, что оправдывает утверждение Ньютона.

Сравнивая силу от кольца HI, вращающегося вокруг PS, с кольцом Hi вокруг PS, отношение этих двух сил равно $d\; 2\; D\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\}\; \{D\; ^\; \{2\}\}\}\}$.

Разделив дуги AT и Bt на соответствующие бесконечно малые кольца, следует, что отношение силы дуги AT, вращающейся вокруг PS, к силе Bt, вращающейся вокруг pS, равно то же отношение, и аналогичным образом отношение сил дуги TB к силе tA, которые оба вращаются, находятся в одинаковом соотношении.

Следовательно, сила, действующая на частицу на любом расстоянии D от центра полой сферы, обратно пропорциональна $D\; 2\; \{\backslash \; displaystyle\; D\; ^\; \{2\}\}$, что доказывает предложение.

Аналог теоремы об оболочках существует в общей теории относительности (ОТО).

Сферическая симметрия подразумевает, что метрика имеет не зависящую от времени геометрию Шварцшильда, даже если центральная масса подвергается гравитационному коллапсу (Misner et al. 1973; см. теорему Биркгофа ). Таким образом, метрика имеет вид

$ds\; 2\; =\; -\; (1-2\; M\; /\; r)\; dt\; 2\; +\; (1-2\; M\; /\; r)\; -\; 1\; dr\; 2\; +\; r\; 2\; d\; \Omega \; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; -\; (1-2M\; /\; r)\; \backslash ,\; dt\; ^\; \{2\}\; +\; (1-2M\; /\; r)\; ^\; \{-\; 1\}\; dr\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; d\; \backslash \; Omega\; ^\; \{\; 2\}\}$

(с использованием геометрических единиц, где $G\; =\; c\; =\; 1\; \{\backslash \; displaystyle\; G\; =\; c\; =\; 1\}$). Для $r>R>0\; \{\backslash \; displaystyle\; r>R>0\}$(где $R\; \{\backslash \; displaystyle\; R\}$- радиус некоторой массовой оболочки), масса действует как дельта-функция в начале координат. Для оболочки массы могут существовать извне, но чтобы метрика была неособой в начале координат, $M\; \{\backslash \; displaystyle\; M\; \}$должен быть равен нулю в метрике. Это уменьшает метрику до плоского пространства Минковского ; таким образом, внешние оболочки не имеют гравитационного эффекта.

Этот результат освещает гравитационный коллапс, ведущий к черной дыре, и его влияние на движение световых лучей и частиц за пределами и внутри горизонта событий (Hartle 2003, глава 12).

Wikimedia Commons носители, относящиеся к Теорема о оболочке.

• Масштаб высоты