Полугруппа

редактировать

Ассоциативное свойство конкатенации строк.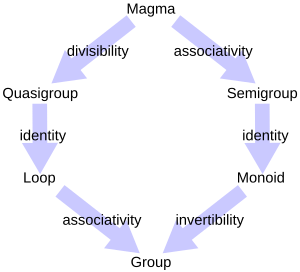

Алгебраические структуры между магмами и группами : Полугруппа - это магма с ассоциативностью. моноид - это полугруппа с элементом идентичности.

В математике полугруппа - это алгебраическая структура, состоящая из множества вместе с ассоциативной бинарной операцией.

Бинарная операция полугруппы чаще всего обозначается мультипликативно : x · y, или просто xy, обозначает результат применение операции полугруппы к упорядоченной паре (x, y). Ассоциативность формально выражается следующим образом: (x · y) · z = x · (y · z) для всех x, y и z в полугруппе.

Полугруппы можно рассматривать как частный случай магм, где операция является ассоциативной, или как обобщение групп, не требуя наличия элемента идентичности или обратное. Как и в случае групп или магм, операция полугруппы не обязательно должна быть коммутативной, поэтому x · y не обязательно равно y · x; Хорошо известным примером ассоциативной, но некоммутативной операции является матричное умножение. Если полугрупповая операция коммутативна, то полугруппа называется коммутативной полугруппой или (реже, чем в аналогичном случае групп ) ее можно назвать абелевой полугруппой.

A моноид представляет собой алгебраическую структуру, промежуточную между группами и полугруппами, и представляет собой полугруппу, имеющую единичный элемент, таким образом подчиняясь всем аксиомам группы, кроме одной; наличие обратных точек от моноида не требуется. Естественный пример - строки с конкатенацией в качестве двоичной операции и пустой строкой в качестве элемента идентификации. Ограничение непустыми строками дает пример полугруппы, которая не является моноидом. Положительные целые числа с добавлением образуют коммутативную полугруппу, которая не является моноидом, тогда как неотрицательные целые числа образуют моноид. Полугруппу без элемента идентичности можно легко превратить в моноид, просто добавив элемент идентичности. Следовательно, моноиды изучаются в теории полугрупп, а не в теории групп. Полугруппы не следует путать с квазигруппами, которые являются обобщением групп в другом направлении; операция в квазигруппе не обязательно должна быть ассоциативной, но квазигруппы сохраняют от групп понятие деления. Деление на полугруппы (или на моноиды) вообще невозможно.

Формальное изучение полугрупп началось в начале 20 века. Ранние результаты включают теорему Кэли для полугрупп, реализующую любую полугруппу как полугруппу преобразований, в которой произвольные функции заменяют роль биекций из теории групп. Глубокий результат в классификации конечных полугрупп - теория Крона – Родса, аналогичная разложению Джордана – Гёльдера для конечных групп. Некоторые другие методы изучения полугрупп, такие как отношения Грина, ни на что не похожи в теории групп.

Теория конечных полугрупп имела особое значение в теоретической информатике с 1950-х годов из-за естественной связи между конечными полугруппами и конечными автоматами через синтаксический моноид. В теории вероятностей полугруппы связаны с марковскими процессами. В других областях прикладной математики полугруппы являются фундаментальными моделями для линейных систем, не зависящих от времени. В уравнениях с частными производными полугруппа связана с любым уравнением, пространственная эволюция которого не зависит от времени.

Существует множество специальных классов полугрупп, полугрупп с дополнительными свойствами, которые появляются в конкретных приложениях. Некоторые из этих классов даже ближе к группам, поскольку демонстрируют некоторые дополнительные, но не все свойства группы. Из них отметим: регулярные полугруппы, ортодоксальные полугруппы, полугруппы с инволюцией, инверсные полугруппы и полугруппы с сокращением. Есть также интересные классы полугрупп, которые не содержат никаких групп, кроме тривиальной группы ; примерами последнего типа являются бэнды и их коммутативный подкласс - полурешетки, которые также являются упорядоченными алгебраическими структурами.

Содержание

1 Определение
2 Примеры полугруппы
3 Основные понятия
- 3.1 Тождество и ноль
- 3.2 Подполугруппы и идеалы
- 3.3 Гомоморфизмы и конгруэнции
- 3.4 Факторы и деления
4 Структура полугрупп
5 Специальные классы полугрупп
6 Структурная теорема для коммутативных полугрупп
7 Группа дробей
8 Полугрупповые методы в уравнениях с частными производными
9 История
10 Обобщения
11 См. Также
12 Примечания
13 Цитаты
14 Ссылки

Определение

Полугруппа - это набор $S {\ displaystyle S}$ $S$ вместе с двоичным операция " $⋅ {\ displaystyle \ cdot}$ $\cdot$ " (то есть функция $⋅: S × S → S {\ displaystyle \ cdot: S \ times S \ rightarrow S}$ $\cdot:S\times S\rightarrow S$ ), который удовлетворяет ассоциативному свойству :

для всех

a, b, c ∈ S {\ displaystyle a, b, c \ in S}

a,b,c\in S

, уравнение

(a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) {\ displaystyle (a \ cdot b) \ cdot c = a \ cdot (b \ cdot c)}

(a\cdot b)\cdot c = a\cdot(b\cdot c)

верен.

Более кратко, полугруппа - это ассоциативная магма.

Примеры полугрупп

Пустая полугруппа : пустой набор образует полугруппу с пустой функцией в качестве бинарной операции.
Полугруппа с одним элементом : по существу существует только один (а именно, только один до изоморфизма ), синглтон {a} с операцией a · a = a.
Полугруппа с двумя элементами : есть пять, которые существенно отличаются друг от друга.
Моноид «триггер»: полугруппа с тремя элементами, представляющими три операции на переключателе - установка, сброс и бездействие.
Множество положительных целых чисел с добавлением. (При включении 0 это становится моноидом.)
Набором целых чисел с минимумом или максимумом. (С включенной положительной / отрицательной бесконечностью это становится моноидом.)
Квадрат неотрицательных матриц заданного размера с матричным умножением.
Любой идеал кольца с умножением кольца.
Множество всех конечных строк над фиксированным алфавитом Σ с конкатенацией строк в качестве полугрупповой операции - так называемая «свободная полугруппа над Σ ". С включенной пустой строкой эта полугруппа становится свободным моноидом над Σ.
A распределением вероятностей F вместе со всеми степенями свертки F, со сверткой в качестве Это называется полугруппой свертки.
Полугруппы преобразований и моноиды.
Набор непрерывных функций из топологического пространства в себя с композицией функций образует моноид с тождественной функцией Действуя как личность. В более общем смысле, эндоморфизмы любого объекта категории образуют моноид при композиции.

Основные концепции

Идентичность и ноль

A левой идентичности полугруппы $S {\ displaystyle S}$ $S$ (или, в более общем смысле, magma ) - это элемент $e {\ displaystyle e}$ $e$ так, что для всех $x {\ displaystyle x}$ $x$ в $S {\ displaystyle S}$ $S$ , $ex = x {\ displaystyle ex = x}$ $ex=x$ . Аналогично, правый идентификатор представляет собой элемент $f {\ displaystyle f}$ $f$ такой, что для всех $x {\ displaystyle x}$ $x$ в $S {\ displaystyle S}$ $S$ , $xf = x {\ displaystyle xf = x}$ $xf=x$ . И левая, и правая идентичности называются односторонними идентичностями . Полугруппа может иметь одну или несколько левых идентичностей, но не иметь правой идентичности, и наоборот.

A двусторонняя идентичность (или просто identity ) - это элемент, который является одновременно левой и правой идентичностью. Полугруппы с двусторонней идентичностью называются моноидами. Полугруппа может иметь не более одной двусторонней идентичности. Если полугруппа имеет двустороннюю идентичность, то двусторонняя идентичность является единственной односторонней идентичностью в полугруппе. Если полугруппа имеет как левую, так и правую идентичность, то она имеет двустороннюю идентичность (которая, следовательно, является уникальной односторонней идентичностью).

Полугруппа $S {\ displaystyle S}$ $S$ без идентичности может быть встроена в моноид, образованный присоединением элемента $e ∉ S {\ displaystyle e \ notin S}$ $e \notin S$ до $S {\ displaystyle S}$ $S$ и определение $e ⋅ s = s ⋅ e = s {\ displaystyle e \ cdot s = s \ cdot e = s}$ $e \cdot s = s \cdot e = s$ для всех $s ∈ S ∪ {e} {\ displaystyle s \ in S \ cup \ {e \}}$ $s \in S \cup \{e\}$ . Обозначение $S 1 {\ displaystyle S ^ {1}}$ $S^{1}$ обозначает моноид, полученный из $S {\ displaystyle S}$ $S$ путем присоединения идентификатора, если необходимо ( $S 1 = S {\ displaystyle S ^ {1} = S}$ $S^{1}=S$ для моноида).

Аналогично, каждая магма имеет не более одного поглощающего элемента, который в теории полугрупп называется нулем . Аналогично приведенной выше конструкции для каждой полугруппы $S {\ displaystyle S}$ $S$ можно определить $S 0 {\ displaystyle S ^ {0}}$ $S^{0}$ , a полугруппа с 0, которая вкладывает $S {\ displaystyle S}$ $S$ .

Подполугруппы и идеалы

Операция полугруппы индуцирует операцию над набором ее подмножеств: данные подмножества A и B полугруппы S, их произведение A · B, обычно обозначаемое как AB, является множеством {ab | a в A и b в B}. (Это понятие определяется идентично как для групп.) В терминах этой операции подмножество A называется

a подполугруппой, если AA является подмножеством A,
a правый идеал, если AS является подмножеством A, и
a левым идеалом, если SA является подмножеством A.

Если A является одновременно левым идеалом и правым идеалом, то он называется идеал (или двусторонний идеал ).

Если S - полугруппа, то пересечение любого набора подполугрупп S также является подполугруппой S. Таким образом, подполугруппы S образуют полную решетку.

Пример полугруппы с минимальный идеал не является множеством натуральных чисел при добавлении. Минимальный идеал коммутативной полугруппы, если он существует, является группой.

Отношения Грина, набор из пяти отношений эквивалентности, которые характеризуют элементы с точки зрения основных идеалов, которые они порождают, являются важными инструментами для анализа идеалов полугруппы. и связанные с ним понятия структуры.

Подмножество со свойством, что каждый элемент коммутирует с любым другим элементом полугруппы, называется центром полугруппы. Центр полугруппы на самом деле является подполугруппой.

Гомоморфизмы и сравнения

A полугруппа гомоморфизм - это функция, сохраняющая структуру полугруппы. Функция f: S → T между двумя полугруппами является гомоморфизмом, если уравнение

f (ab) = f (a) f (b).

выполняется для всех элементов a, b в S, т. Е. Результат то же самое при выполнении операции полугруппы после или до применения отображения f.

Гомоморфизм полугрупп между моноидами сохраняет идентичность, если это гомоморфизм моноидов. Но есть гомоморфизмы полугрупп, которые не являются гомоморфизмами моноидов, например каноническое вложение полугруппы $S {\ displaystyle S}$ $S$ без идентичности в $S 1 {\ displaystyle S ^ {1}}$ $S^{1}$ . Условия, характеризующие гомоморфизмы моноидов, обсуждаются далее. Пусть $f: S 0 → S 1 {\ displaystyle f: S_ {0} \ to S_ {1}}$ $f:S_0\to S_1$ - гомоморфизм полугрупп. Образ $f {\ displaystyle f}$ $f$ также является полугруппой. Если $S 0 {\ displaystyle S_ {0}}$ $S_{0}$ - моноид с элементом идентичности $e 0 {\ displaystyle e_ {0}}$ $e_{0}$ , то $f (e 0) {\ displaystyle f (e_ {0})}$ $f(e_0)$ - элемент идентичности в изображении $f {\ displaystyle f}$ $f$ . Если $S 1 {\ displaystyle S_ {1}}$ $S_{1}$ также является моноидом с элементом идентичности $e 1 {\ displaystyle e_ {1}}$ $e_{1}$ и $e 1 {\ displaystyle e_ {1}}$ $e_{1}$ принадлежит изображению $f {\ displaystyle f}$ $f$ , тогда $f (e 0) = e 1 {\ displaystyle f (e_ {0}) = e_ {1}}$ $f(e_0)=e_1$ , т.е. $f {\ displaystyle f}$ $f$ - моноидный гомоморфизм. В частности, если $f {\ displaystyle f}$ $f$ является сюръективным, то это моноидный гомоморфизм.

Две полугруппы S и T называются изоморфными, если существует биекция f: S ↔ T со свойством, что для любых элементов a, b в S, f (ab) = f (a) f (b). Такое же строение имеют изоморфные полугруппы.

A полугрупповая конгруэнция $∼ {\ displaystyle \ sim}$ $\sim$ - это отношение эквивалентности, которое совместимо с полугрупповой операцией. То есть подмножество $∼ ⊆ S × S {\ displaystyle \ sim \; \ substeq S \ times S}$ $\sim\;\subseteq S\times S$ , которое является отношением эквивалентности, и $x ∼ y {\ displaystyle x \ sim y \,}$ $x\sim y\,$ и $u ∼ v {\ displaystyle u \ sim v \,}$ $u\sim v\,$ подразумевает $xu ∼ yv {\ displaystyle xu \ sim yv \, }$ $xu\sim yv\,$ для каждого $x, y, u, v {\ displaystyle x, y, u, v}$ $x,y,u,v$ в S. Как и любое отношение эквивалентности, полугрупповая конгруэнция $∼ {\ displaystyle \ sim}$ $\sim$ индуцирует классы конгруэнтности

[a] ∼ = {x ∈ S | x ∼ a} {\ displaystyle [a] _ {\ sim} = \ {x \ in S \ vert \; x \ sim a \}}

[a]_\sim = \{x\in S\vert\; x\sim a\}

, а полугрупповая операция вызывает двоичную операцию $∘ {\ displaystyle \ circ}$ $\circ$ в классах конгруэнтности:

[u] ∼ ∘ [v] ∼ = [uv] ∼ {\ displaystyle [u] _ {\ sim} \ circ [v] _ { \ sim} = [uv] _ {\ sim}}

[u]_\sim\circ [v]_\sim = [uv]_\sim

Поскольку $∼ {\ displaystyle \ sim}$ $\sim$ является конгруэнцией, набор всех классов конгруэнтности $∼ {\ displaystyle \ sim}$ $\sim$ образует полугруппу с $∘ {\ displaystyle \ circ}$ $\circ$ , называемую полугруппой частных или полугруппой факторов и обозначается $S / ∼ {\ displaystyle S / \ sim}$ $S/\sim$ . Отображение $x ↦ [x] ∼ {\ displaystyle x \ mapsto [x] _ {\ sim}}$ $x \mapsto [x]_\sim$ является гомоморфизмом полугрупп, называемым факторным отображением, каноническая проекция или проекция ; если S - моноид, то фактор-полугруппа - это моноид с тождеством $[1] ∼ {\ displaystyle [1] _ {\ sim}}$ $[1]_\sim$ . Наоборот, ядро любого гомоморфизма полугрупп является конгруэнцией полугрупп. Эти результаты являются не чем иным, как конкретизацией первой теоремы об изоморфизме в универсальной алгебре. Классы конгруэнтности и фактор-моноиды являются объектами изучения в системах переписывания строк..

A ядерное сравнение на S является ядром эндоморфизма S.

Полугруппа S удовлетворяет условие максимума для сравнений, если любое семейство конгруэнций на S, упорядоченное по включению, имеет максимальный элемент. По лемме Цорна это равносильно утверждению, что выполняется условие возрастающей цепи : не существует бесконечной строго возрастающей цепи сравнений на S.

Каждый идеал I полугруппа индуцирует подполугруппу, фактор-полугруппу Рисса посредством сравнения x ρ y ⇔ либо x = y, либо оба x и y находятся в I.

Факторы и деления

Следующие понятия вводят идею о том, что одна полугруппа содержится в другой.

Полугруппа T является фактором полугруппы S, если существует сюръективный морфизм полугруппы от S до T . Например, $(Z / 2 Z, +) {\ displaystyle (\ mathbb {Z} / 2 \ mathbb {Z}, +)}$ $(\mathbb {Z} /2\mathbb {Z},+)$ является частным от $(Z / 4 Z, +) {\ displaystyle (\ mathbb {Z} / 4 \ mathbb {Z}, +)}$ $(\mathbb {Z} /4\mathbb {Z},+)$ , используя морфизм, состоящий из взятия остатка по модулю 2 от целое число.

Полугруппа T делит полугруппу S, отмеченную $T ⪯ S {\ displaystyle T \ prevq S}$ $T\preceq S$ if T является фактором подполугруппы S . В частности, подполугруппы S делят T, хотя не обязательно, что существует частное S.

. Оба этих отношения транзитивны.

Структура полугрупп

Для любого подмножества A группы S существует наименьшая подполугруппа T группы S, содержащая A, и мы говорим, что A порождает T. Один элемент x из S порождает подполугруппу {x | n ∈ Z }. Если это конечно, то говорят, что x имеет конечный порядок, в противном случае он имеет бесконечный порядок . Полугруппа называется периодической, если все ее элементы имеют конечный порядок. Полугруппа, порожденная одним элементом, называется моногенной (или циклической ). Если моногенная полугруппа бесконечна, то она изоморфна полугруппе положительных целых чисел с операцией сложения. Если он конечный и непустой, то он должен содержать хотя бы один идемпотент. Отсюда следует, что каждая непустая периодическая полугруппа имеет хотя бы один идемпотент.

Подгруппа, которая также является группой, называется подгруппой. Между подгруппами полугруппы и ее идемпотентами существует тесная связь. Каждая подгруппа содержит ровно один идемпотент, а именно единичный элемент подгруппы. Для каждого идемпотента e полугруппы существует единственная максимальная подгруппа, содержащая e. Таким образом возникает каждая максимальная подгруппа, поэтому между идемпотентами и максимальными подгруппами существует взаимно однозначное соответствие. Здесь термин максимальная подгруппа отличается от его стандартного использования в теории групп.

Чаще можно сказать, когда порядок конечен. Например, каждая непустая конечная полугруппа периодична, имеет минимальный идеал и хотя бы один идемпотент. Количество конечных полугрупп данного размера (больше 1) (очевидно) больше, чем количество групп того же размера. Например, из шестнадцати возможных «таблиц умножения» для набора из двух элементов {a, b} восемь образуют полугруппы, тогда как только четыре из них являются моноидами и только две образуют группы. Подробнее о структуре конечных полугрупп см. Теория Крона – Родса.

Специальные классы полугрупп

A моноид - это полугруппа с единичным элементом.
A группа - полугруппа с элементом идентичности и обратным элементом .
Подполугруппа - это подмножество полугруппы, которое закрывается при операции полугруппы.
A полугруппа отмены имеет свойство отмены : a · b = a · c подразумевает b = c, и аналогично для b · a = c · a.
A band - это полугруппа, операция которой идемпотентная.
A полурешетка - это полугруппа, чьи операции являются идемпотентными и коммутативными.
0-простыми полугруппами.
Полугруппы преобразований : любая конечная полугруппа S может быть представлена преобразования множества (состояний) Q не более чем | S | +1 состояния. Каждый элемент x из S затем отображает Q в себя x: Q → Q, а последовательность xy определяется как q (xy) = (qx) y для каждого q в Q. Очевидно, что последовательность является ассоциативной операцией, здесь эквивалентной функции состав. Это представление является базовым для любого автомата или конечного автомата (FSM).
бициклическая полугруппа фактически является моноидом, который может быть описана как свободная полугруппа на двух образующих p и q при соотношении pq = 1.
C0-полугруппы.
Регулярные полугруппы. Каждый элемент x имеет по крайней мере один обратный y, удовлетворяющий xyx = x и yxy = y; элементы x и y иногда называют «взаимно обратными».
Обратные полугруппы - это регулярные полугруппы, в которых каждый элемент имеет ровно одну обратную. В качестве альтернативы регулярная полугруппа обратна тогда и только тогда, когда любые два идемпотента коммутируют.
Аффинная полугруппа: полугруппа, изоморфная конечно порожденной подполугруппе Z. Эти полугруппы имеют приложения к коммутативной алгебре.

Структурная теорема для коммутативных полугрупп

Существует структурная теорема для коммутативных полугрупп в терминах полурешеток. Полурешетка (или, точнее, полурешетка) $(L, ≤) {\ displaystyle (L, \ leq)}$ $(L, \le)$ - это частично упорядоченное множество, где каждая пара элементы $a, b ∈ L {\ displaystyle a, b \ in L}$ $a,b \in L$ имеет наибольшую нижнюю границу, обозначенную $a ∧ b {\ displaystyle a \ wedge б}$ $a\wedge b$ . Операция $∧ {\ displaystyle \ wedge}$ $\wedge$ превращает $L {\ displaystyle L}$ $L$ в полугруппу, удовлетворяющую дополнительному закону идемпотентности $a ∧ a = a {\ displaystyle a \ wedge a = a}$ $a \wedge a = a$ .

Учитывая гомоморфизм $f: S → L {\ displaystyle f: S \ to L}$ $f: S \to L$ из произвольной полугруппы в полурешетку каждое обратное изображение $S a = f - 1 {a} {\ displaystyle S_ {a} = f ^ {- 1} \ {a \}}$ $S_a = f^{-1} \{a \}$ является (возможно, пустым) полугруппа. Кроме того, $S {\ displaystyle S}$ $S$ становится с оценкой на $L {\ displaystyle L}$ $L$ в том смысле, что

$S a S b ⊆ S a ∧ b {\ displaystyle S_ {a} S_ {b} \ substeq S_ {a \ wedge b}}$ $S_a S_b \subseteq S_{a \wedge b}$

Если $f {\ displaystyle f}$ $f$ находится на, полурешетка $L {\ displaystyle L}$ $L$ изоморфна частному от $S {\ displaystyle S}$ $S$ по отношению эквивалентности $∼ {\ displaystyle \ sim}$ $\sim$ такое, что $x ∼ y {\ displaystyle x \ sim y}$ $x \sim y$ iff $f (x) = f (y) {\ Displaystyle f (x) = f (y)}$ $f(x) = f(y)$ . Это отношение эквивалентности является полугрупповой конгруэнцией, как определено выше.

Всякий раз, когда мы берем фактор коммутативной полугруппы по конгруэнции, мы получаем другую коммутативную полугруппу. Структурная теорема гласит, что для любой коммутативной полугруппы $S {\ displaystyle S}$ $S$ существует тончайшее сравнение $∼ {\ displaystyle \ sim}$ $\sim$ такое, что частное из $S {\ displaystyle S}$ $S$ по этому отношению эквивалентности является полурешеткой. Обозначая эту полурешетку $L {\ displaystyle L}$ $L$ , мы получаем гомоморфизм $f {\ displaystyle f}$ $f$ из $S {\ displaystyle S}$ $S$ на $L {\ displaystyle L}$ $L$ . Как упоминалось, $S {\ displaystyle S}$ $S$ становится градуированным этой полурешеткой.

Кроме того, все компоненты $S a {\ displaystyle S_ {a}}$ $S_a$ являются архимедовыми полугруппами. Архимедова полугруппа - это полугруппа, в которой для любой пары элементов $x, y {\ displaystyle x, y}$ $x, y$ существует элемент $z {\ displaystyle z}$ $z$ и $n>0 {\ displaystyle n>0}$ $n>0$ таким образом, чтобы $xn = yz {\ displaystyle x ^ {n} = yz}$ $x^n = y z$ .

Архимедово свойство непосредственно следует из порядка в полурешетке $L \ displaystyle L}$ $L$ , поскольку при таком порядке мы имеем $f (x) ≤ f (y) {\ displaystyle f (x) \ leq f (y)}$ $f(x) \le f(y)$ if и только если $xn = yz {\ displaystyle x ^ {n} = yz}$ $x^n = y z$ для некоторых $z {\ displaystyle z}$ $z$ и $n>0 {\ displaystyle n>0}$ $n>0$ .

Группа фракций

группа фракций или завершение группы полугруппы S - это группа G = G (S) генерируется элементами S как образующими и всеми уравнениями xy = z, которые выполняются в S как отношения. Существует очевидный гомоморфизм полугрупп j: S → G (S), который переводит каждый элемент S в соответствующий генератор. Это имеет универсальное свойство для морфизмов из S в группу: для любой группы H и любого гомоморфизма полугрупп k: S → H существует единственный групповой гомоморфизм f: G → H с k = fj. Мы можем думать о G как о «самой общей» группе, содержащей гомоморфный образ S.

. Важный вопрос состоит в том, чтобы охарактеризовать те полугруппы, для которых это отображение является вложением. Это не всегда так: например, возьмем S в качестве полугруппы подмножеств некоторого множества X с теоретико-множественным пересечением в качестве бинарной операции (это пример полурешетки). Поскольку A.A = A выполняется для всех элементов S, это должно быть верно и для всех образующих G (S): таким образом, это тривиальная группа . Очевидно, что для встраиваемости S необходимо иметь свойство отмены . Когда S коммутативна, этого условия также достаточно, и группа Гротендика полугруппы обеспечивает конструкцию группы дробей. Проблема для некоммутативных полугрупп восходит к первой содержательной статье о полугруппах. Анатолий Мальцев дал необходимые и достаточные условия вложимости в 1937 году.

Методы полугрупп в дифференциальных уравнениях с частными производными

Теория полугрупп может быть использована для изучения некоторых задач в области дифференциальных уравнений в частных производных. Грубо говоря, полугрупповой подход состоит в том, чтобы рассматривать зависящее от времени уравнение в частных производных как обыкновенное дифференциальное уравнение на функциональном пространстве. Например, рассмотрим следующую начальную / краевую задачу для уравнения теплопроводности на пространственном интервале (0, 1) ⊂ R и временах t ≥ 0:

{∂ tu (t, x) = ∂ x 2 u (t, x), x ∈ (0, 1), t>0; u (t, x) = 0, x ∈ {0, 1}, t>0; U (T, Икс) знак равно U 0 (Икс), Икс ∈ (0, 1), T = 0. {\ Displaystyle {\ begin {cases} \ partial _ {t} u (t, x) = \ partial _ {x} ^ {2} u (t, x), x \ in (0,1), t>0; \\ u (t, x) = 0, x \ in \ {0,1 \}, t>0; \\ u (t, x) = u_ {0} (x), x \ in (0,1), t = 0. \ End {ases}}}

\begin{cases} \partial_{t} u(t, x) = \partial_{x}^{2} u(t, x), x \in (0, 1), t>0; \\ u (t, x) = 0, x \ in \ {0, 1 \}, t>0; \\ u (t, x) = u_ {0} (x), x \ in (0, 1), t = 0. \ end {ases}

Пусть X = L ((0, 1) R ) будет L пространство суммируемых с квадратом вещественных функций с областью определения интервал (0, 1), и пусть A - оператор второй производной с областью определения

D (A) = {u ∈ ЧАС 2 ((0, 1); R) | U (0) = u (1) = 0}, {\ displaystyle D (A) = {\ big \ {} u \ in H ^ {2} ((0, 1); \ mathbf {R}) {\ big |} u (0) = u (1) = 0 {\ big \}},}

D(A) = \big\{ u \in H^{2} ((0, 1); \mathbf{R}) \big| u(0) = u(1) = 0 \big\},

, где H - пространство Соболева. Тогда указанная выше начальная / краевая задача может быть интерпретирована как начальная задача для обыкновенного дифференциального уравнения в пространстве X:

{u ˙ (t) = A u (t); u (0) = u 0. {\ displaystyle {\ begin {cases} {\ dot {u}} (t) = Au (t); \\ u (0) = u_ {0}. \ end {cases}}}

\begin{cases} \dot{u}(t) = A u (t); \\ u(0) = u_{0}. \end{cases}

По эвристике уровень, решение этой проблемы «должно» быть u (t) = exp (tA) u 0. Однако для строгого рассмотрения Ent, значение должно быть придано экспоненте tA. Как функция от t, exp (tA) представляет собой полугруппу операторов из X в себя, переводящую начальное состояние u 0 в момент времени t = 0 в состояние u (t) = exp (tA) u 0 в момент времени t. Оператор A называется инфинитезимальным генератором полугруппы.

История

Изучение полугрупп отставало от изучения других алгебраических структур с более сложными аксиомами, такими как группы или кольца. Ряд источников приписывают первое употребление термина (на французском языке) Ж.-А. де Сегье в Élements de la Théorie des Groupes Abstraits (Элементы теории абстрактных групп) в 1904 году. Этот термин используется в английском языке в 1908 году в Теории групп конечного порядка Гарольда Хинтона.

Антон Сушкевич получил первые нетривиальные результаты о полугруппах. Его статья 1928 года "Über die endlichen Gruppen ohne das Gesetz der eindeutigen Umkehrbarkeit" ("О конечных группах без правила единственной обратимости") определила структуру конечных простых полугрупп и показала, что минимальный идеал (или Отношения Грина J-класс) конечной полугруппы просты. С этого момента основы теории полугрупп были заложены Дэвидом Рисом, Джеймсом Александром Грином, Альфредом Х. Клиффордом и Гордоном Престоном. Последние два опубликовали двухтомную монографию по теории полугрупп в 1961 и 1967 годах соответственно. В 1970 году новое периодическое издание под названием Semigroup Forum (в настоящее время редактируется Springer Verlag ) стало одним из немногих математических журналов, полностью посвященных теории полугрупп.

теория представлений полугрупп была разработана в 1963 году Борисом Шейном с использованием бинарных отношений на множестве A и композиции отношений. для продукта полугруппы. На алгебраической конференции в 1972 году Шайн провел обзор литературы по B A, полугруппе отношений на A. В 1997 году Шейн и Ральф Маккензи доказали, что каждая полугруппа изоморфна транзитивной полугруппе бинарные отношения.

В последние годы исследователи в этой области стали более специализированными, появились специальные монографии по важным классам полугрупп, например инверсные полугруппы, а также монографии, посвященные приложениям, в частности для конечных автоматов, а также в функциональном анализе.

Обобщения

Группоподобные структуры
	Тотальность	Ассоциативность	Идентичность	Обратимость	Коммутативность
Полугруппоид	Ненужно	Обязательно	Ненужно	Ненужно	Ненужно
Малая категория	Ненужно	Обязательно	Обязательно	Ненужно	Ненужно
Группоид	Ненужно	Обязательно	Обязательно	Обязательно	Ненужно
Магма	Требуется	Ненужно	Ненужно	Ненужно	Ненужно
Quasigroup	Требуется	Ненужно	Ненужно	Требуется	Ненужно
Единичная магма	Требуется	Ненужно	Требуется	Ненужно	Ненужно
Цикл	Требуется	Ненужно	Требуется	Требуется	Ненужно
Полугруппа	Требуется	Обязательно	Ненужно	Ненужно	Ненужно
Инверсная полугруппа	Обязательно	Обязательно	Ненужно	Требуется	Не требуется
Моноид	Требуется	Требуется	Требуется	Ненужно	Ненужно
Коммутативный моноид	Требуется	Требуется	Требуется	Ненужно	Требуется
Группа	Требуется	Обязательно	Обязательно	Обязательно	Ненужно
Абелева группа	Обязательно	Обязательно	Обязательно	Обязательно	Обязательно
^αЗамыкание, которое используется во многих источниках, является аксиомой, эквивалентной тотальности, хотя и определяется по-другому.

Если отбросить аксиому ассоциативности полугруппы, результатом будет магма, which is nothing more than a set M equipped with a binary operation that is closed M × M → M.

Generalizing in a different direction, an n-ary semigroup(also n-semigroup, polyadic semigroupor multiary semigroup) is a generalization of a semigroup to a set G with a n-ary operation instead of a binary operation. The associative law is generalized as follows: ternary associativity is (abc)de = a(bcd)e = ab(cde), i.e. the string abcde with any three adjacent elements bracketed. N-ary associativity is a string of length n + (n − 1) with any n adjacent elements bracketed. A 2-ary semigroup is just a semigroup. Further axioms lead to an n-ary group.

A third generalization is the semigroupoid, in which the requirement that the binary relation be total is lifted. As categories generalize monoids in the same way, a semigroupoid behaves much like a category but lacks identities.

Infinitary generalizations of commutative semigroups have sometimes been considered by various authors.