Феномен Рунге

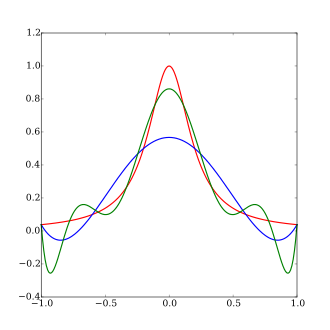
Функция Рунге (красный, самый высокий центральный пик); интерполирующий полином 5-го порядка с равноотстоящими интерполирующими точками (синий, нижний центральный пик); и интерполирующий полином 9-го порядка с равноотстоящими интерполирующими точками (зеленый, средний центральный пик)

В математической области численного анализа, явление Рунга ( немецкое: [ʁʊŋə] ) является проблемой колебаний на краях интервала, который происходит при использовании полиномиальной интерполяции с полиномами высокой степени над набором эквидистантен расположенными точки интерполяции. Он был открыт Карлом Дэвидом Толме Рунге (1901) при исследовании поведения ошибок при использовании полиномиальной интерполяции для аппроксимации определенных функций. Открытие было важным, потому что оно показывает, что переход к более высоким степеням не всегда улучшает точность. Это явление аналогично явлению Гиббса в приближении ряда Фурье.

СОДЕРЖАНИЕ

• 1 Введение
• 2 Проблема
  • 2.1 Причина
• 3 Смягчения проблемы
  • 3.1 Изменение точек интерполяции
  • 3.2 Алгоритм S-Рунге без передискретизации
  • 3.3 Использование кусочно-полиномов
  • 3.4 Ограниченная минимизация
  • 3.5 Подгонка наименьших квадратов
  • 3.6 Полином Бернштейна
  • 3.7 Интерполяция внешних ложных ограничений
• 4 Связанные утверждения теории приближений
• 5 См. Также
• 6 Ссылки

Вступление

В теореме Вейерштрасса приближение гласит, что для каждой непрерывной функции F ( х), определенной на интервале [, Ь ], существует набор полиномиальных функций Р п ( х) при п = 0, 1, 2,..., каждый из степени не более n, что приближает f ( x) с равномерной сходимостью по [ a, b ], когда n стремится к бесконечности, то есть

${\ Displaystyle \ lim _ {п \ вправо \ infty} \ влево (\ макс _ {а \ Leq х \ Leq b} \ влево | е (х) -P_ {п} (х) \ вправо | \ вправо) = 0.}$

Рассмотрим случай, когда кто -то желает интерполировать через п + 1 эквидистантно расположенных точек функции F ( х) с помощью п - градусный многочлен Р п ( х), который проходит через эти точки. Естественно, из теоремы Вейерштрасса можно было ожидать, что использование большего количества точек приведет к более точному восстановлению f ( x). Однако не гарантируется, что этот конкретный набор полиномиальных функций P n ( x) обладает свойством равномерной сходимости; в теореме только утверждается, что существует набор полиномиальных функций, но не дается общий метод их нахождения.

Р п ( х), полученный таким образом, может в действительности расходятся от F ( х), как п возрастает; обычно это происходит в виде колеблющегося рисунка, который увеличивается ближе к концам точек интерполяции. Это явление приписывают Рунге.

Проблема

Рассмотрим функцию Рунге

${\ Displaystyle е (х) = {\ гидроразрыва {1} {1 + 25x ^ {2}}} \,}$

(масштабная версия Ведьмы Агнеси ). Рунге обнаружил, что если эта функция интерполируется в эквидистантных точках x i между -1 и 1 таким образом, что:

${\ displaystyle x_ {i} = {\ frac {2i} {n}} - 1, \ quad i \ in \ left \ {0,1, \ dots, n \ right \}}$

с полиномом P n ( x) степени ≤  n, результирующая интерполяция колеблется к концу интервала, то есть близко к -1 и 1. Можно даже доказать, что ошибка интерполяции увеличивается (без ограничений), когда степень полином увеличивается:

${\ Displaystyle \ lim _ {п \ вправо \ infty} \ влево (\ макс _ {- 1 \ Leq х \ Leq 1} | е (х) -P_ {п} (х) | \ вправо) = \ infty. }$

Это показывает, что полиномиальная интерполяция высокой степени в равноотстоящих точках может быть проблематичной.

Причина

Феномен Рунге является следствием двух свойств этой проблемы.

• Величина производных n-го порядка этой конкретной функции быстро растет с увеличением n.
• Эквидистантность между точками приводит к постоянной Лебега, которая быстро увеличивается с увеличением n.

Это явление графически очевидно, потому что оба свойства в совокупности увеличивают величину колебаний.

Ошибка между производящей функцией и интерполяционным полиномом порядка n определяется выражением

${\ displaystyle f (x) -P_ {n} (x) = {\ frac {f ^ {(n + 1)} (\ xi)} {(n + 1)!}} \ prod _ {i = 0 } ^ {n} (x-x_ {i})}$

для некоторых из (−1, 1). Таким образом, ${\ displaystyle \ xi}$

${\ Displaystyle \ макс _ {- 1 \ leq x \ leq 1} | f (x) -P_ {n} (x) | \ leq \ max _ {- 1 \ leq x \ leq 1} {\ frac {\ left | f ^ {(n + 1)} (x) \ right |} {(n + 1)!}} \ max _ {- 1 \ leq x \ leq 1} \ prod _ {i = 0} ^ { п} | х-х_ {i} |}$.

Обозначим узловой функцией ${\ Displaystyle W_ {п} (х)}$

${\ displaystyle w_ {n} (x) = (x-x_ {0}) (x-x_ {1}) \ cdots (x-x_ {n})}$

и пусть будет максимум величины функции: ${\ displaystyle W_ {n}}$${\ displaystyle w_ {n}}$

${\ Displaystyle W_ {n} = \ max _ {- 1 \ leq x \ leq 1} | w_ {n} (x) |}$.

Элементарно доказать, что при равноудаленных узлах

${\ Displaystyle W_ {п} \ leq п! ч ^ {п + 1}}$

где - размер шага. ${\ displaystyle h = 2 / n}$

Кроме того, предположим, что ( n +1) -я производная от ограничена, т. Е. ${\ displaystyle f}$

${\ Displaystyle \ макс _ {- 1 \ Leq х \ Leq 1} | е ^ {(п + 1)} (х) | \ Leq M_ {п + 1}}$.

Следовательно,

${\ displaystyle \ max _ {- 1 \ leq x \ leq 1} | f (x) -P_ {n} (x) | \ leq M_ {n + 1} {\ frac {h ^ {n + 1}} {(n + 1)}}}$.

Но величина ( n +1) -й производной функции Рунге увеличивается с увеличением n, т. К. Следствием этого является то, что результирующая верхняя граница,, стремится к бесконечности, когда n стремится к бесконечности. ${\ Displaystyle М_ {п + 1} \ leq (п + 1)! 5 ^ {п + 1}}$${\ Displaystyle (10 / п) ^ {п + 1} п!}$

Хотя это часто используется для объяснения феномена Рунге, тот факт, что верхняя граница ошибки стремится к бесконечности, конечно, не обязательно означает, что сама ошибка также расходится с n.

Смягчение проблемы

Изменение точек интерполяции

Колебание можно минимизировать, используя узлы, которые более плотно распределены по краям интервала, в частности, с асимптотической плотностью (на интервале [-1,1]), задаваемой формулой. Стандартный пример такого набора узлов - узлы Чебышева, для которых максимальная ошибка аппроксимации функции Рунге гарантированно уменьшается с увеличением полиномиального порядка. Это явление демонстрирует, что многочлены высокой степени обычно не подходят для интерполяции с равноудаленными узлами. ${\ displaystyle 1 / {\ sqrt {1-x ^ {2}}}}$

Алгоритм S-Рунге без передискретизации

Когда необходимо использовать эквидистантные выборки, поскольку повторная выборка на наборах узлов с хорошим поведением невозможна, можно рассмотреть алгоритм S-Рунге. В этом подходе исходный набор узлов отображается на набор узлов Чебышева, обеспечивая стабильную полиномиальную реконструкцию. Особенность этого метода в том, что нет необходимости в передискретизации отображаемых узлов, которые также называются фальшивыми узлами. Python выполнение этой процедуры можно найти здесь.

Использование кусочно-полиномов

Этой проблемы можно избежать, используя сплайновые кривые, которые являются кусочно-полиномами. При попытке уменьшить ошибку интерполяции можно увеличить количество частей полинома, которые используются для построения сплайна, вместо увеличения степени используемых полиномов.

Ограниченная минимизация

Можно также подобрать полином более высокой степени (например, с точками использовать полином порядка вместо) и подобрать интерполирующий полином, первая (или вторая) производная которого имеет минимальную норму. ${\ displaystyle n}$${\ Displaystyle N = п ^ {2}}$${\ displaystyle n + 1}$ ${\ displaystyle L ^ {2}}$

Аналогичный подход заключается в минимизации ограниченной версии расстояния между производной полинома и средним значением его производной. Явно, чтобы минимизировать ${\ Displaystyle L ^ {p}}$${\ Displaystyle м ^ {\ mathrm {th}}}$${\ Displaystyle м ^ {\ mathrm {th}}}$

${\ displaystyle V_ {p} = \ int _ {a} ^ {b} \ left | {\ frac {\ operatorname {d} ^ {m} P_ {N} (x)} {\ operatorname {d} x ^ {m}}} - {\ frac {1} {ba}} \ int _ {a} ^ {b} {\ frac {\ operatorname {d} ^ {m} P_ {N} (z)} {\ operatorname {d} z ^ {m}}} \ operatorname {d} z \ right | ^ {p} \ operatorname {d} x- \ sum _ {i = 1} ^ {n} \ lambda _ {i} \, \ left (P_ {N} (x_ {i}) - f (x_ {i}) \ right),}$

где и в отношении коэффициентов полинома и множителей Лагранжа,. Когда, уравнения связи, генерируемые множителями Лагранжа, сводятся к минимальному многочлену, который проходит через все точки. На противоположном конце будет приближаться форма, очень похожая на приближение кусочно-полиномов. Когда, в частности, приближается к линейным кусочно-полиномам, т.е. соединяет точки интерполяции прямыми линиями. ${\ Displaystyle N \ GEQ п-1}$${\ displaystyle m lt;N}$ ${\ displaystyle \ lambda _ {i}}$${\ Displaystyle N = п-1}$${\ Displaystyle P_ {N} (х)}$${\ displaystyle n}$${\ displaystyle \ lim _ {N \ rightarrow \ infty} P_ {N} (x)}$${\ displaystyle m = 1}$${\ displaystyle \ lim _ {N \ rightarrow \ infty} P_ {N} (x)}$

Роль, которую играет в процессе минимизации, состоит в том, чтобы контролировать важность размера флуктуаций от среднего значения. Чем больше, тем больше штрафуются большие колебания по сравнению с небольшими. Самым большим преимуществом евклидовой нормы является то, что она допускает аналитические решения и гарантирует, что будет иметь только один минимум. Когда может быть несколько минимумов, трудно гарантировать, что конкретный найденный минимум будет глобальным минимумом, а не локальным. ${\ displaystyle p}$${\ displaystyle V_ {p}}$${\ displaystyle p}$${\ displaystyle p = 2}$${\ displaystyle V_ {p}}$${\ displaystyle p \ neq 2}$${\ displaystyle V_ {p}}$

Подгонка наименьших квадратов

Другой метод - подгонка полинома меньшей степени с использованием метода наименьших квадратов. Как правило, при использовании равноотстоящих точек приближение наименьших квадратов хорошо обусловлено. ${\ displaystyle m}$${\ displaystyle N lt;2 {\ sqrt {m}}}$${\ Displaystyle P_ {N} (х)}$

Многочлен Бернштейна

Используя многочлены Бернштейна, можно равномерно аппроксимировать каждую непрерывную функцию в отрезке, хотя этот метод довольно затратен в вычислительном отношении.

Интерполяция внешних фальшивых ограничений

Этот метод предлагает оптимально сложить плотное распределение ограничений типа P "(x) = 0 на узлах, расположенных снаружи около конечных точек каждой стороны интервала интерполяции, где P" (x) - вторая производная полинома интерполяции. Эти ограничения называются внешними фиктивными ограничениями, поскольку они не принадлежат интервалу интерполяции и не соответствуют поведению функции Рунге. Метод продемонстрировал, что он имеет лучшую производительность интерполяции, чем кусочные полиномы (сплайны), чтобы смягчить явление Рунге.

Связанные утверждения из теории приближений

Для каждой предопределенной таблицы узлов интерполяции существует непрерывная функция, для которой последовательность полиномов интерполяции на этих узлах расходится. Для каждой непрерывной функции существует таблица узлов, на которых сходится процесс интерполяции. Чебышёвская интерполяция (т. Е. На чебышёвских узлах ) сходится равномерно для любой абсолютно непрерывной функции.

Смотрите также

• Сравните с явлением Гиббса для синусоидальных базисных функций
• Серия Тейлора
• Чебышевские узлы
• Фонарь Шварца, еще один пример неудачной конвергенции
• Теорема Стоуна – Вейерштрасса

использованная литература

1. ^ Рунге, Карл (1901), "Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten", Zeitschrift für Mathematik und Physik, 46: 224–243.доступно на www.archive.org
2. ^ Эпперсон, Джеймс (1987). «На примере Рунге». Амер. Математика. Ежемесячно. 94: 329–341. DOI : 10.2307 / 2323093.
3. ^ Беррут, Жан-Поль; Trefethen, Ллойд Н. (2004), "Барицентрическое Лагранжа интерполяции", SIAM Обзор, 46 (3): 501-517, CiteSeerX   10.1.1.15.5097, DOI : 10,1137 / S0036144502417715, ISSN   1095-7200
4. ^ Де Марчи, Стефано; Маркетти, Франческо; Перраккионе, Эмма; Poggiali, Davide (2020), «Полиномиальная интерполяция с помощью отображенных баз без повторной выборки», J. Comput. Прил. Математика., 364, DOI : 10.1016 / j.cam.2019.112347, ISSN 0377-0427  
5. ^ Дальквист, Germund ; Бьорк, Оке (1974), «4.3.4. Эквидистантная интерполяция и феномен Рунге», Численные методы, стр.  101–103, ISBN   0-13-627315-7
6. ^ Белэнджер, Николас (2017), Интерполяция внешних поддельных ограничений: конец феномена Рунге с многочленами высокой степени, опирающимися на равномерно распределенные узлы - Приложение к планированию движения воздушной робототехники (PDF), Труды 5-го института математики и его прикладная конференция по математике в обороне
7. ^ Чейни, Уорд; Свет, Уилл (2000), Курс теории приближений, Брукс / Коул, стр. 19, ISBN   0-534-36224-9