Правило смесей

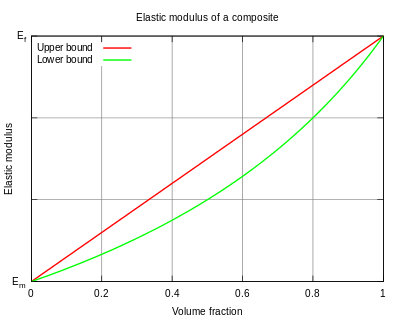
Верхняя и нижняя границы модуля упругости композитного материала, как предсказывается правилом смесей. Фактический модуль упругости находится между кривыми.

В науке материалов, A общее правило смесей является взвешенное среднее используется для прогнозирования различных свойств композиционного материала. Он обеспечивает теоретические верхние и нижние границы таких свойств, как модуль упругости, массовая плотность, предел прочности при растяжении, теплопроводность и электропроводность. Как правило, существует две модели: одна для осевой нагрузки (модель Фойгта) и одна для поперечной нагрузки (модель Рейсса).

В общем, для некоторых свойств материала (часто модуля упругости) правило смесей гласит, что общее свойство в направлении, параллельном волокнам, может достигать ${\ displaystyle E}$

${\ displaystyle E_ {c} = fE_ {f} + \ left (1-f \ right) E_ {m}}$

где

• ${\ displaystyle f = {\ frac {V_ {f}} {V_ {f} + V_ {m}}}}$это объемная доля волокон
• ${\ displaystyle E_ {f}}$ это свойство материала волокон
• ${\ displaystyle E_ {m}}$ материальное свойство матрицы

В случае модуля упругости он известен как модуль верхней границы и соответствует нагрузке, параллельной волокнам. Обратное правило смесей состояний, в направлении, перпендикулярном к волокнам, модуль упругости композита может быть как

${\ displaystyle E_ {c} = \ left ({\ frac {f} {E_ {f}}} + {\ frac {1-f} {E_ {m}}} \ right) ^ {- 1}.}$

Если исследуемым свойством является модуль упругости, эта величина называется модулем нижней границы и соответствует поперечной нагрузке.

• 1 Вывод для модуля упругости
  • 1.1 Модуль верхней границы
  • 1.2 Модуль нижней границы
• 2 Другая недвижимость
• 3 См. Также
• 4 ссылки
• 5 Внешние ссылки

Модуль верхней границы

Рассмотрим композитный материал при одноосном растяжении. Чтобы материал оставался неповрежденным, деформация волокон должна равняться деформации матрицы. Следовательно , закон Гука для одноосного растяжения дает ${\ displaystyle \ sigma _ {\ infty}}$${\ displaystyle \ epsilon _ {f}}$${\ displaystyle \ epsilon _ {m}}$

${\ displaystyle {\ frac {\ sigma _ {f}} {E_ {f}}} = \ epsilon _ {f} = \ epsilon _ {m} = {\ frac {\ sigma _ {m}} {E_ { m}}}}$

( 1)

где,,, являются напряжение и модуль упругости волокон и матрицы, соответственно. Учитывая, что напряжение - это сила на единицу площади, баланс сил дает, что ${\ displaystyle \ sigma _ {f}}$${\ displaystyle E_ {f}}$${\ displaystyle \ sigma _ {m}}$${\ displaystyle E_ {m}}$

${\ Displaystyle \ сигма _ {\ infty} = е \ сигма _ {е} + \ влево (1-е \ вправо) \ сигма _ {м}}$

( 2)

где - объемная доля волокон в композите (и - объемная доля матрицы). ${\ displaystyle f}$${\ displaystyle 1-f}$

Если предположить, что композитный материал ведет себя как линейно-упругий материал, т. Е. Подчиняется закону Гука для некоторого модуля упругости композита и некоторой деформации композита, то уравнения 1 и 2 можно объединить, чтобы получить ${\ displaystyle \ sigma _ {\ infty} = E_ {c} \ epsilon _ {c}}$${\ displaystyle E_ {c}}$${\ displaystyle \ epsilon _ {c}}$

${\ displaystyle E_ {c} \ epsilon _ {c} = fE_ {f} \ epsilon _ {f} + \ left (1-f \ right) E_ {m} \ epsilon _ {m}.}$

Наконец, поскольку общий модуль упругости композита можно выразить как ${\ displaystyle \ epsilon _ {c} = \ epsilon _ {f} = \ epsilon _ {m}}$

${\ displaystyle E_ {c} = fE_ {f} + \ left (1-f \ right) E_ {m}.}$

Модуль нижней границы

Теперь пусть композитный материал загружен перпендикулярно волокнам, предполагая это. Общая деформация в композите распределяется между материалами таким образом, что ${\ Displaystyle \ sigma _ {\ infty} = \ sigma _ {f} = \ sigma _ {m}}$

${\ displaystyle \ epsilon _ {c} = f \ epsilon _ {f} + \ left (1-f \ right) \ epsilon _ {m}.}$

В этом случае общий модуль упругости материала определяется выражением

${\ displaystyle E_ {c} = {\ frac {\ sigma _ {\ infty}} {\ epsilon _ {c}}} = {\ frac {\ sigma _ {f}} {f \ epsilon _ {f} + \ left (1-f \ right) \ epsilon _ {m}}} = \ left ({\ frac {f} {E_ {f}}} + {\ frac {1-f} {E_ {m}}} \ right) ^ {- 1}}$

так как,. ${\ displaystyle \ sigma _ {f} = E \ epsilon _ {f}}$${\ displaystyle \ sigma _ {m} = E \ epsilon _ {m}}$

Подобные выводы дают правила смесей для

• плотность вещества

${\ displaystyle \ left ({\ frac {f} {\ rho _ {f}}} + {\ frac {1-f} {\ rho _ {m}}} \ right) ^ {- 1} \ leq \ rho _ {c} \ leq f \ rho _ {f} + \ left (1-f \ right) \ rho _ {m}}$

• предел прочности на растяжение

${\ displaystyle \ left ({\ frac {f} {\ sigma _ {UTS, f}}} + {\ frac {1-f} {\ sigma _ {UTS, m}}} ​​\ right) ^ {- 1 } \ leq \ sigma _ {UTS, c} \ leq f \ sigma _ {UTS, f} + \ left (1-f \ right) \ sigma _ {UTS, m}}$

• теплопроводность

${\ displaystyle \ left ({\ frac {f} {k_ {f}}} + {\ frac {1-f} {k_ {m}}} \ right) ^ {- 1} \ leq k_ {c} \ leq fk_ {f} + \ left (1-f \ right) k_ {m}}$

• электрическая проводимость

${\ displaystyle \ left ({\ frac {f} {\ sigma _ {f}}} + {\ frac {1-f} {\ sigma _ {m}}} \ right) ^ {- 1} \ leq \ сигма _ {c} \ leq f \ sigma _ {f} + \ left (1-f \ right) \ sigma _ {m}}$

При рассмотрении эмпирической корреляции некоторых физических свойств и химического состава соединений другие соотношения, правила или законы также очень напоминают правило смесей:

• Закон Амагата - Закон парциальных объемов газов
• Уравнение Гладстона – Дейла - Оптический анализ жидкостей, стекол и кристаллов.
• Закон Коппа - использует массовую долю
• Закон Коппа – Неймана - Теплоемкость сплавов
• Закон Вегарда - Параметры кристаллической решетки

• Калькулятор правил смесей