Роза (математика)

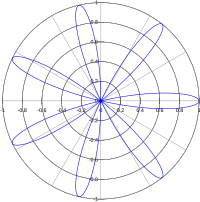
Роза с 7 лепестками (k = 7) Роза с 8 лепестками (k = 4). Кривые розы определены как $r\; =\; cos\; \; k\; \theta \; \{\backslash \; displaystyle\; r\; =\; \backslash \; cos\; k\; \backslash \; theta\}$для различных значений k = n / d.

В математике, роза или кривая родонеи - это синусоида, построенная в полярных координатах.

• 1 Общий обзор
• 2 Область
• 3 Как параметр k влияет на формы
• 4 Параметр смещения
• 5 Программирование
• 6 См. Также
• 7 Примечания
• 8 Внешние ссылки

До подобия все эти кривые можно выразить полярным уравнением вида

$r\; =\; cos\; \; (k\; \theta )\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; R\; =\; \backslash \; cos\; (k\; \backslash \; theta)\; \}$

или, как вариант, в виде пары декартовых параметрических уравнений вида

$x\; =\; cos\; \; (k\; \theta )\; cos\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; X\; =\; \backslash \; cos\; (k\; \backslash \; theta)\; \backslash \; соз\; (\backslash \; theta)\}$

$Y\; =\; соз\; \; (к\; \theta )\; грех\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; y\; =\; \backslash \; cos\; (k\; \backslash \; theta)\; \backslash \; sin\; (\backslash \; theta)\}$

Если k является целым числом, кривая будет иметь форму розы с

• 2k лепестками, если k четное, и
• k лепестками, если k нечетное.

Когда k четное, весь график розы будет отслеживаться ровно один раз, когда значение тета, θ, изменится с 0 на 2 $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$. Если k нечетное, это произойдет в интервале от 0 до $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$. (В более общем смысле это произойдет на любом интервале длины 2 $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$для четного k и $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$для нечетного k.)

Если k является полуцелым числом (например, 1/2, 3/2, 5/2), кривая будет иметь форму розы с 4k лепестками. Пример: n = 7, d = 2, k = n / d = 3,5, когда θ изменяется с 0 на 4 $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$.

Если k можно выразить как n ± 1/6, где n - ненулевое целое число, кривая будет иметь форму розы с 12 тыс. лепестков.

Если k можно выразить как n / 3, где n - целое число, не делящееся на 3, кривая будет иметь форму розы с n лепестками, если n нечетное, и 2n лепестками, если n четное.

Если k является рациональным, то кривая является замкнутой и имеет конечную длину. Если k иррационально, то он не замкнут и имеет бесконечную длину. Более того, график розы в этом случае образует плотное множество (то есть он сколь угодно близко подходит к каждой точке единичного круга).

Поскольку

$грех\; \; (k\; \theta )\; =\; соз\; \; (k\; \theta \; -\; \pi \; 2)\; =\; соз\; \; (k\; (\theta \; -\; \pi \; 2\; k))\; \{\backslash \; displaystyle\; \backslash \; sin\; (k\; \backslash \; theta)\; =\; \backslash \; cos\; \backslash \; left\; (k\; \backslash \; theta\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; =\; \backslash \; cos\; \backslash \; left\; (k\; \backslash \; left\; (\backslash \; theta\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2k\}\}\; \backslash \; right)\; \backslash \; right)\}$

для всех $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, кривые, заданные полярными уравнениями

$r\; =\; sin\; \; (k\; \theta )\; \{\backslash \; displaystyle\; \backslash ,\; r\; =\; \backslash \; sin\; (k\; \backslash \; theta)\}$и $r\; =\; cos\; \; (k\; \theta )\; \{\backslash \; displaystyle\; \backslash ,\; r\; =\; \backslash \; cos\; (k\; \backslash \; theta)\}$

идентичны, за исключением поворот на $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$/ 2k радиан.

Кривые Родонеи были названы итальянским математиком Гвидо Гранди между 1723 и 1728 годами.

Роза, полярное уравнение которой имеет вид форма

$r\; =\; a\; соз\; \; (k\; \theta )\; \{\backslash \; displaystyle\; r\; =\; a\; \backslash \; cos\; (k\; \backslash \; theta)\; \backslash ,\}$

, где k - целое положительное число, имеет площадь

$1\; 2\; \int \; 0\; 2\; \pi \; (a\; соз\; \; (к\; \theta ))\; 2\; d\; \theta \; =\; a\; 2\; 2\; (\pi \; +\; sin\; \; (4\; k\; \pi )\; 4\; k)\; =\; \pi \; a\; 2\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{2\; \backslash \; pi\}\; (a\; \backslash \; cos\; (k\; \backslash \; theta))\; ^\; \{2\}\; \backslash ,\; d\; \backslash \; theta\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; left\; (\backslash \; pi\; +\; \{\backslash \; frac\; \{\backslash \; sin\; (4k\; \backslash \; pi)\}\; \{4k\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; pi\; a\; ^\; \{2\}\}\; \{2\}\}\}$

, если k четное, и

$1\; 2\; \int \; 0\; \pi \; (a\; соз\; \; (k\; \theta ))\; 2\; d\; \theta \; =\; a\; 2\; 2\; (\pi \; 2\; +\; sin\; \; (2\; k\; \pi )\; 4\; k)\; =\; \pi \; a\; 2\; 4\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; (a\; \backslash \; cos\; (k\; \backslash \; theta))\; ^\; \{2\}\; \backslash ,\; d\; \backslash \; theta\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{\backslash \; sin\; (2k\; \backslash \; pi)\}\; \{4k\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; pi\; a\; ^\; \{2\}\}\; \{4\}\}\; \}$

, если k нечетное.

То же самое относится к розам с полярными уравнениями вида

$r\; =\; a\; sin\; \; (k\; \theta )\; \{\backslash \; displaystyle\; r\; =\; a\; \backslash \; sin\; (k\; \backslash \; theta)\; \backslash ,\}$

, поскольку их графики - это просто жесткие вращения роз, определенных с помощью косинуса.

В форме k = n для целого числа n форма будет похожа на цветок. Если n нечетное, половина из них будет перекрываться, образуя цветок с n лепестками. Однако, если n равно, лепестки не будут перекрываться, образуя цветок с 2n лепестками.

Когда d - простое число, тогда n / d - наименее распространенная форма, и лепестки будут вытягиваться вокруг, чтобы перекрывать другие лепестки. Количество лепестков, каждый из которых перекрывается, равно тому, как далеко в последовательности простых чисел это простое число равно +1, т.е. 2 равно 2, 3 равно 3, 5 равно 4, 7 равно 5 и т. Д.

В форма k = 1 / d, когда d четно, она будет выглядеть как серия петель d / 2, которые встречаются в 2 небольших петлях в центре, касаясь (0, 0) от вертикали и симметричных относительно оси x. Если d нечетное, тогда у него будет d / 2 петель, которые встречаются в небольшой петле в центре либо слева (когда в форме d = 4n - 1), либо справа (d = 4n + 1).

Если d не является простым, а n не равно 1, то это будет отображаться как серия взаимосвязанных циклов.

Если k - иррациональное число (например, $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$, $2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{2\}\}\}$и т. Д.), То кривая будет иметь бесконечно много лепестков, и она будет плотной в единичном диске.

Примеры роз, созданных с использованием шестерен с разным передаточным числом n = 1, d = 1, k = 1. n = 1, d = 3, k≈0,333 n = 3, d = 1, k = 3 n = 4, d = 5, k = 0.8 Воспроизвести мультимедиа Эффект анимации изменения параметра смещения

Добавление параметра смещения c, поэтому полярный уравнение принимает вид

$r\; =\; cos\; \; (k\; \theta )\; +\; c\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; r\; =\; \backslash \; cos\; (k\; \backslash \; theta)\; +\; c\}$

изменяет форму, как показано справа. В случае, когда параметр k является нечетным целым числом, две перекрывающиеся половины кривой разделяются, когда смещение изменяется от нуля.

BBC BASIC для Windows

rem bbc basic для Windows k = 4 r = 100: rem radius origin 200,200: rem разместить ориентацию на экране для t = 0, чтобы 20 шаг 1 / (4 * pi * 10) x = r * (cos (k * t) * cos (t)) y = r * (cos (k * t) * sin (t)) график x * 2, y * 2: rem double для графического разрешения next

R

k <- 4 t <- seq(0, 4*pi, length.out=500) x <- cos(k*t)*cos(t) y <- cos(k*t)*sin(t) plot(x,y, type="l", col="blue")

MATLAB и OCTAVE

function rose (del_theta, k, ampitude)% input:% del_theta = del_theta - размер дискретного шага для дискретизации непрерывного диапазона углов от 0 до 2 * pi% k = лепестковый коэффициент%, если k нечетное, тогда k - количество лепестков%, если k четное, тогда k - половина количества лепестков.% Амплитуда = длина каждого лепестка.% Выводит:% 2D-график из вызова этого функция иллюстрирует пример тригонометрии и двумерного декартового построения theta = 0: del_theta: 2 * pi; x = амплитуда * cos (k * theta). * cos (theta); y = амплитуда * cos (k * theta). * sin (theta); plot (x, y)

JavaScript и p5.js

k = n / d; beginShape (); for (let a = 0; a < d.value() * TWO_PI; a += 0.05) { let r = 100 * sin(k * a); let x = r * cos(a); let y = r * sin(a); vertex(x, y); } endShape();

• кривая Лиссажу
• quadrifolium - кривая розы, где k = 2.
• роза Маурера
• роза (топология)
• спирограф

Викискладе есть медиафайлы, связанные с кривыми Роуз.

• Вайсштейн, Эрик У. «Роза». MathWorld.
• Апплет для создания розы с параметром k
• Визуальный словарь специальных плоских кривых Xah Lee
• Интерактивный пример с JSXGraph
• Интерактивный пример с p5