Пульсация (электрическая)

Пульсация (в частности, пульсация напряжения ) в электронике - это остаточное периодическое изменение постоянного напряжения в источнике питания, полученное от источника переменного тока (AC). Эта пульсация возникает из-за неполного подавления переменного сигнала после исправления. Пульсации напряжения возникают на выходе выпрямителя или при генерации и коммутации постоянного тока.

Пульсации (в частности, пульсирующий ток или импульсный ток ) также может относиться к импульсному потреблению тока нелинейными устройствами, такими как выпрямители с конденсаторным входом.

Помимо этих изменяющихся во времени явлений, существует частотная область пульсация, которая возникает в некоторых классах фильтра и других обработка сигналов сети. В этом случае периодическое изменение - это изменение вносимых потерь сети по сравнению с увеличением частоты. Вариация не может быть строго линейно-периодической. В этом смысле также пульсацию обычно следует рассматривать как случайный эффект, поскольку ее существование является компромиссом между величиной пульсации и другими параметрами конструкции.

Пульсация - это бесполезная трата энергии и имеет множество нежелательных эффектов в цепи постоянного тока: она нагревает компоненты, вызывает шум и искажения, а также может привести к неправильной работе цифровых схем. Пульсации можно уменьшить с помощью электронного фильтра и устранить с помощью регулятора напряжения.

• 1 Пульсации напряжения
  • 1.1 Фильтрация
• 2 Фильтрация в источниках питания
• 3 Входные фильтры конденсатора и дросселя
  • 3.1 В зависимости от сопротивления нагрузки
  • 3.2 В зависимости от последовательного дросселя
  • 3.3 Регулировка напряжения
  • 3.4 Влияние пульсаций
• 4 Ток пульсаций
• 5 Частота -домен пульсации
• 6 См. также
• 7 Примечания
• 8 Ссылки

Неидеальную форму волны постоянного напряжения можно рассматривать как составную часть постоянного постоянного тока. составляющая (смещение) с наложенным переменным (AC) напряжением - пульсирующим напряжением. Составляющая пульсаций часто мала по величине по сравнению с составляющей постоянного тока, но в абсолютном выражении пульсации (как в случае систем передачи HVDC ) могут составлять тысячи вольт. Сама пульсация представляет собой составную (несинусоидальную) форму волны, состоящую из гармоник некоторой основной частоты, которая обычно является исходной частотой сети переменного тока, но в случае импульсных источников питания основная частота может быть десятками килогерц в мегагерцы. Характеристики и составляющие пульсаций зависят от их источника: бывает однофазное полу- и двухполупериодное выпрямление, а также трехфазное полу- и двухполупериодное выпрямление. Выпрямление может быть управляемым (с использованием кремниевых выпрямителей (SCR)) или неконтролируемым (с использованием диодов). Кроме того, имеется активное выпрямление, в котором используются транзисторы.

В зависимости от применения могут иметь значение различные свойства пульсаций напряжения: уравнение пульсаций для анализа Фурье для определения составляющих гармоник; пиковое (обычно размах) значение напряжения; среднеквадратичное значение (RMS) напряжения, которое является составляющей передаваемой мощности; коэффициент пульсации γ, отношение среднеквадратичного значения к выходному напряжению постоянного тока; коэффициент преобразования (также называемый коэффициентом выпрямления или «КПД») η, отношение выходной мощности постоянного тока к входной мощности переменного тока; и форм-фактор - отношение среднеквадратичного значения выходного напряжения к среднему значению выходного напряжения. Аналогичные отношения для выходного тока пульсаций также могут быть вычислены.

Электронный фильтр с высоким импедансом на частоте пульсаций может использоваться для уменьшения напряжения пульсаций и увеличения или уменьшения выхода постоянного тока; такой фильтр часто называют сглаживающим фильтром.

. Первым этапом преобразования переменного тока в постоянный является пропускание переменного тока через выпрямитель. В этой ситуации выходное пульсирующее напряжение очень велико; размах напряжения пульсаций равен пиковому напряжению переменного тока минус прямое напряжение выпрямительных диодов. В случае кремниевого диода SS прямое напряжение составляет 0,7 В; для ламповых выпрямителей прямое напряжение обычно находится в диапазоне от 25 до 67 В (5R4). Выходное напряжение представляет собой синусоидальную волну с инвертированными отрицательными полупериодами. Уравнение:

$V\; L\; (t)\; =\; V\; A\; C\; p\; \cdot \; |\; sin\; \; (t)\; |\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{L\}\}\; (t)\; =\; V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\; \backslash \; cdot\; |\; \backslash \; sin\; (t)\; |\}$

Расширение Фурье функции:

$VL\; (t)\; знак\; равно\; 2\; VAC\; p\; \pi \; +\; 4\; VAC\; p\; \pi \; \cdot \; \sum \; n\; =\; 1\; \infty \; cos\; \; (n\; \pi )\; 1\; -\; 4\; n\; 2\; \cdot \; cos\; \; (2\; n\; \omega \; t)\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{L\}\; \}\; (t)\; =\; \{\backslash \; frac\; \{2V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; pi\}\}\; +\; \{\backslash \; frac\; \{4V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; pi\}\}\; \backslash \; cdot\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; cos\; (n\; \backslash \; pi)\}\; \{1-4n\; ^\; \{2\}\}\}\; \backslash \; cdot\; \backslash \; cos\; (2n\; \backslash \; omega\; t)\}$

Несколько соответствующие свойства очевидны при рассмотрении ряда Фурье:

• постоянный (наибольший) член $2\; VAC\; p\; \pi \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{2V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; pi\}\; \}\}$должно быть постоянное напряжение
• основная (линейная частота) отсутствует
• расширение состоит только из четных гармоник основной гармоники
• амплитуда гармоник пропорциональна $1\; n\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{n\; ^\; \{2\}\}\}\}$где $n\; \{\backslash \; displaystyle\; n\}$- порядок гармоники
• член для гармоники второго порядка $4\; ВА.\; С\; п\; 3\; \pi \; соз\; \; (2\; \omega \; t)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{4V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{3\; \backslash \; pi\}\}\; \backslash \; cos\; (2\; \backslash \; omega\; t)\}$часто используется для представления всего напряжения пульсаций для упрощения вычислений.

Выходные напряжения:

$VL = VAC = VAC p 2 (без учета падения и потерь на диодах) VDC = 1 T ∫ 0 TVL (t) dt = 1 π [- cos ⁡ (t)] 0 π = - cos ⁡ (π) - - cos ⁡ (0) = 2 VAC p π V rms = 1 T ∫ 0 T (VL (t) - K) 2 dt = 1 T ∫ 0 TVL (t) 2 - 2 KVL (t) + K 2 dt = 1 π [1 2 t - 1 4 sin ⁡ (t) + 2 K cos ⁡ (t) + K 2 t] 0 π = 1 π (π 2 - 4 KVAC p + K 2 π), пусть K = VDC, и подставим его в VAC p, так что = 1 2-8 π 2 VAC p 2 + 4 π 2 VAC p 2 = (VAC p 2) 2 - (2 В переменного тока p π) 2 {\ displaystyle {\ begin {align} V _ {\ mathrm {L}} = {} V _ {\ mathrm {AC}} = {\ frac {V _ {\ mathrm {AC_ { p}}}} {\ sqrt {2}}} \ quad {\ text {(без учета падения и потерь на диодах)}} \\ [6pt] V _ {\ mathrm {DC}} = {} {\ frac {1 } {T}} \ int _ {0} ^ {T} \! V _ {\ mathrm {L}} (t) \, dt = {\ frac {1} {\ pi}} {\ Big [} - \ cos (t) {\ Big]} _ {0} ^ {\ pi} = - \ cos (\ pi) - \ cos (0) \, = {\ frac {2V _ {\ mathrm {AC_ {p}}}} {\ pi}} \\ [6pt] V _ {\ mathrm {rms} } = {} {\ sqrt {{\ frac {1} {T}} \ int _ {0} ^ {T} \! (V _ {\ mathrm {L}} (t) \, - K) ^ { 2} dt}} = {\ sqrt {{\ frac {1} {T}} \ int _ {0} ^ {T} \! V _ {\ mathrm {L}} (t) ^ {2} \, - 2KV _ {\ mathrm {L}} (t) + K ^ {2} dt}} \\ [6pt] = {} {\ sqrt {{\ frac {1} {\ pi}} \ left [{\ frac {1} {2}} t - {\ frac {1} {4}} \ sin (t) + 2K \ cos (t) + K ^ {2} t \ right] _ {0} ^ {\ pi} }} = {\ sqrt {{\ frac {1} {\ pi}} \ left ({\ frac {\ pi} {2}} - 4KV _ {\ mathrm {AC_ {p}}} + K ^ {2}) \ pi \ right)}} \\ [6pt] {\ text {let}} K = V _ {\ mathrm {DC}}, {\ text {и замените в терминах}} V _ {\ mathrm {AC_ {p }}}, {\ text {so}} \\ = {} {\ sqrt {{\ frac {1} {2}} - {\ frac {8} {\ pi ^ {2}}} V _ {\ mathrm {AC_ {p}}} ^ {2} + {\ frac {4} {\ pi ^ {2}}} V _ {\ mathrm {AC_ {p}}} ^ {2}}} = {\ sqrt { \ left ({\ frac {V _ {\ mathrm {AC_ {p}}}} {\ sqrt {2}}} \ right) ^ {2} - \ left ({\ frac {2V _ {\ mathrm {AC_ {p }}}} {\ pi}} \ right) ^ {2}}} \ end {align}}}$

$V\; rms\; =\; 2\; VAC\; p\; \pi \; \pi \; 2\; 8\; -\; 1\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; text\; \{rms\}\; \}\; =\; \{\backslash \; frac\; \{2V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; pi\}\}\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{\backslash \; pi\; ^\; \{2\}\}\; \{8\}\}\; -\; 1\}\}\}$

где

• $VL\; \{\; \backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{L\}\}\}$- изменяющееся во времени напряжение на нагрузке, $|\; sin\; \; (t)\; |\; \{\backslash \; displaystyle\; |\; \backslash \; sin\; (t)\; |\}$для периода от 0 до T
• $T\; \{\backslash \; displaystyle\; T\}$- период $VL\; \{\backslash \; displaystyle\; V\_\; \{\; \backslash \; mathrm\; \{L\}\}\}$, можно принять как $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$радиан

Коэффициент пульсации:

$\gamma \; =\; V\; rms\; VDC\; =\; \pi \; 2\; 8-1\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{rms\}\}\}\; \{V\; \_\; \{\backslash \; mathrm\; \{DC\}\}\}\}\; =\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{\backslash \; pi\; ^\; \{\; 2\}\}\; \{8\}\}\; -\; 1\}\}\}$

$\gamma \; \approx \; 0,483\; \{\backslash \; displaystyle\; \backslash \; gamma\; \backslash \; приблизительно\; 0,483\}$

Форм-фактор:

$FF\; =\; VLVDC\; =\; VAC\; p\; 2\; 2\; VAC\; p\; \pi \; \{\; \backslash \; Displaystyle\; FF\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{L\}\}\}\; \{V\; \_\; \{\backslash \; mathrm\; \{DC\}\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \{\backslash \; frac\; \{2V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; pi\}\}\}\}$

$FF\; =\; \pi \; 2\; 2\; \approx \; 1.11\; \{\backslash \; displaystyle\; FF\; =\; \{\backslash \; frac\; \{\backslash \; pi\; \}\; \{2\; \{\backslash \; sqrt\; \{2\}\}\}\}\; \backslash \; приблизительно\; 1,11\}$

Коэффициент пика:

$PF\; =\; VAC\; p\; VAC\; p\; 2\; \{\backslash \; displaystyle\; PF\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{\; p\}\}\}\}\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{\backslash \; sqrt\; \{2\}\}\}\}\}$

$PF\; =\; 2\; \{\backslash \; displaystyle\; PF\; =\; \{\backslash \; sqrt\; \{2\}\}\}$

Коэффициент преобразования:

$\eta \; \approx \; 0,812\; (81,2\%)\; \{\backslash \; displayst\; yle\; \backslash \; eta\; \backslash \; приблизительно\; 0,812\; \backslash \; (81,2\; \backslash \%)\}$

Коэффициент использования трансформатора:

$T\; U\; F\; \approx \; 0,812\; (мост);\; 0,692\; (центральное\; нажатие)\; \{\backslash \; displaystyle\; TUF\; \backslash \; приблизительно\; 0,812\; \backslash \; (\{\backslash \; text\; \{bridge\}\});\; \backslash \; 0,692\; \backslash \; (\{\backslash \; text\; \{center-tapped\}\})\}$

Фильтрация

Полноволновой центр выпрямитель с конденсаторным фильтром

Уменьшение пульсаций - лишь одно из нескольких основных соображений при проектировании фильтра источника питания. Фильтрация пульсаций напряжения аналогична фильтрации других типов сигналов. Однако при преобразовании мощности переменного / постоянного тока, а также при выработке энергии постоянного тока высокие напряжения и токи или и то, и другое могут выводиться как пульсации. Следовательно, большие дискретные компоненты, такие как электролитические конденсаторы с высоким номинальным током пульсаций, большие дроссели с железным сердечником и силовые резисторы с проволочной обмоткой, лучше всего подходят для уменьшения пульсаций до контролируемых размеров перед передачей тока на компонент IC, например регулятор напряжения, или на нагрузку. Тип необходимой фильтрации зависит от амплитуды различных гармоник пульсаций и требований нагрузки. Например, входная цепь с подвижной катушкой (MC) фонокорректора предусилителя может потребовать уменьшения пульсаций не более чем до нескольких сотен нановольт (10В). Напротив, зарядное устройство, являющееся полностью резистивной схемой, не требует какой-либо фильтрации пульсаций. Поскольку желаемый выход - постоянный ток (по существу, 0 Гц), фильтры пульсаций обычно конфигурируются как фильтры нижних частот, характеризующиеся шунтирующими конденсаторами и последовательными дросселями. Последовательные резисторы могут заменять дроссели для уменьшения выходного постоянного напряжения, а шунтирующие резисторы могут использоваться для регулирования напряжения.

Большинство источников питания теперь имеют переключаемый режим. Требования к фильтрации для таких источников питания намного легче удовлетворить из-за высокой частоты пульсаций волны. Частота пульсаций в импульсных источниках питания не связана с частотой сети, а, напротив, кратна частоте цепи прерывателя , которая обычно находится в диапазоне от 50 кГц до 1 МГц.

Входной фильтр конденсатора (в котором первым компонентом является шунтирующий конденсатор) и входной фильтр дросселя (который имеет последовательный дроссель в качестве первого компонент) может уменьшить пульсации, но иметь противоположное влияние на напряжение и ток, и выбор между ними зависит от характеристик нагрузки. Конденсаторные входные фильтры плохо регулируют напряжение, поэтому их лучше использовать в цепях со стабильными нагрузками и низкими токами (поскольку здесь низкие токи уменьшают пульсации). Входные фильтры дросселя предпочтительны для цепей с переменными нагрузками и высокими токами (поскольку дроссель выдает стабильное напряжение, а более высокий ток означает меньшую пульсацию в этом случае).

Количество реактивных компонентов в фильтре называется его порядком. Каждый реактивный компонент снижает мощность сигнала на 6 дБ / октаву выше (или ниже для фильтра верхних частот) угловой частоты фильтра, так что, например, фильтр нижних частот 2-го порядка снижает сигнал сила на 12 дБ / октаву выше угловой частоты. Резистивные компоненты (включая резисторы и паразитные элементы, такие как DCR дросселей и ESR конденсаторов) также уменьшают мощность сигнала, но их влияние линейно и не зависит от частоты.

Обычно выпрямитель работает в большом сглаживающем конденсаторе, который действует как резервуар. После пика выходного напряжения конденсатор подает ток на нагрузку и продолжает делать это до тех пор, пока напряжение на конденсаторе не упадет до значения, которое теперь возрастает в следующем полупериоде выпрямленного напряжения. В этот момент выпрямитель снова проводит ток и подает ток в резервуар, пока снова не будет достигнуто пиковое напряжение.

В зависимости от сопротивления нагрузки

Если постоянная времени RC велика по сравнению с периодом формы сигнала переменного тока, то достаточно точное приближение может быть выполнено следующим образом: при условии, что напряжение на конденсаторе линейно падает. Еще одно полезное предположение можно сделать, если пульсации малы по сравнению с напряжением постоянного тока. В этом случае фазовый угол , через который проходит выпрямитель, будет небольшим, и можно предположить, что конденсатор полностью разряжается от одного пика до следующего с небольшой потерей точности.

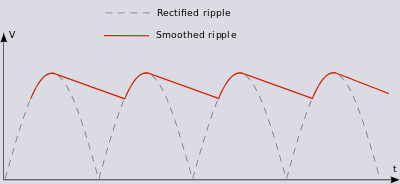Пульсации напряжения от двухполупериодного выпрямителя до и после применения сглаживающего конденсатора

С учетом приведенных выше предположений напряжение пульсаций от пика до пика можно рассчитать следующим образом:

Определение емкости $C\; \{\backslash \; displaystyle\; C\}$и current $I\; \{\backslash \; displaystyle\; I\}$равны

$Q\; =\; CV\; pp\; Q\; =\; Я\; пробыл,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; Q\; =\; CV\; \_\; \{\backslash \; text\; \{pp\}\}\; \backslash \backslash \; Q\; =\; I\; \_\; \{\backslash \; text\; \{ave\}\}\; t\; \_\; \{\backslash \; text\; \{ave\}\},\; \backslash \; end\; \{align\}\; \}\}$

где $Q\; \{\backslash \; displaystyle\; Q\}$- количество заряда. Ток и время $t\; \{\backslash \; displaystyle\; t\}$взяты от начала разряда конденсатора до минимального напряжения двухполупериодного выпрямленного сигнала, как показано на рисунке справа. Тогда время $t\; ave\; \{\backslash \; displaystyle\; t\; \_\; \{\backslash \; text\; \{ave\}\}\}$будет равно половине периода полной входной волны.

$t\; ave\; =\; t\; fullwave\; 2\; =\; 1\; 2\; f\; \{\backslash \; displaystyle\; t\; \_\; \{\backslash \; text\; \{ave\}\}\; =\; \{\backslash \; frac\; \{t\; \_\; \{\backslash \; text\; \{fullwave\}\}\}\; \{2\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\; 2f\}\}\}$

Объединение трех приведенных выше уравнений для определения $V\; pp\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; text\; \{pp\}\}\}$дает,

$V\; pp\; =\; QC\; =\; I\; ave\; t\; аве\; C\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; text\; \{pp\}\}\; =\; \{\backslash \; frac\; \{Q\}\; \{C\}\}\; =\; \{\backslash \; frac\; \{I\; \_\; \{\backslash \; text\; \{ave\}\}\; t\; \_\; \{\backslash \; text\; \{ave\}\}\}\; \{C\}\}\; \}$

Таким образом, для двухполупериодного выпрямителя:

$V\; pp\; =\; I\; 2\; f\; C\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{pp\}\}\; =\; \{\backslash \; frac\; \{I\}\; \{2fC\}\}\}$

где

• $V\; pp\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{pp\}\}\}$- напряжение пульсаций от пика до пика;
• $I\; \{\backslash \; displaystyle\; I\}$- ток в цепи
• $f\; \{\backslash \; displaystyle\; f\}$- частота источника (линии) переменного тока.
• $C\; \{\backslash \; displaystyle\; C\}$- емкость

Для среднеквадратичного значения пульсационного напряжения расчет более сложен, так как форма пульсирующего сигнала влияет на результат. Предположение пилообразной формы волны аналогично предположениям выше. Среднеквадратичное значение пилообразной волны составляет $V\; p\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{p\}\}\}\; \{\backslash \; sqrt\; \{3\}\}\}\}$где $V\; p\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{p\}\}\}$- пиковое напряжение. При дальнейшем приближении $V\; p\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{p\}\}\}$равно $V\; pp\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{pp\}\}\; \}\; \{2\}\}\}$, он дает результат:

$V\; rms\; =\; V\; pp\; 2\; 3\; =\; I\; 4\; 3\; f\; C\; =\; VDC\; 4\; 3\; f\; CR\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{rms\}\; \}\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{pp\}\}\}\; \{2\; \{\backslash \; sqrt\; \{3\}\}\}\}\; =\; \{\backslash \; frac\; \{I\}\; \{4\; \{\backslash \; sqrt\; \{3\}\}\; fC\}\}\; =\; \{\backslash \; frac\; \{\; V\; \_\; \{\backslash \; mathrm\; \{DC\}\}\}\; \{4\; \{\backslash \; sqrt\; \{3\}\}\; fCR\}\}\}$где $VDC\; =\; IR\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{DC\}\}\; =\; IR\}$

$\gamma \; =\; V\; rms\; VDC\; =\; 1\; 4\; 3\; f\; CR\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{rms\}\}\}\; \{V\; \_\; \{\backslash \; mathrm\; \{DC\}\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{4\; \{\backslash \; sqrt\; \{3\}\}\; fCR\}\}\}$$\approx \; 0,453\; XCR\; \{\backslash \; displaystyle\; \backslash \; приблизительно\; 0,453\; \{\backslash \; frac\; \{X\; \_\; \{\backslash \; mathrm\; \{C\}\}\}\; \{R\}\}\}$

где

• $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$- коэффициент пульсации;
• $R\; \{\backslash \; displaystyle\; R\}$- сопротивление нагрузки
• Для приближенной формулы предполагается, что X C>R; это немного больше, чем фактическое значение, потому что пилообразная волна содержит нечетные гармоники, которых нет в выпрямленном напряжении.

В зависимости от последовательного дросселя

Другой подход к уменьшению пульсаций - использование серия дроссель. Дроссель имеет фильтрующее действие и, следовательно, обеспечивает более плавную форму волны с меньшим количеством гармоник высокого порядка. Напротив, выход постоянного тока близок к среднему входному напряжению, в отличие от напряжения с накопительного конденсатора, которое близко к пиковому входному напряжению. Начиная с члена Фурье для второй гармоники и игнорируя высшие гармоники,

$V\; 2\; f\; (t)\; =\; 4\; VAC\; p\; 3\; \pi \; cos\; \; (2\; \omega \; t)\; \{\backslash \; displaystyle\; V\; \_\; \{\backslash \; mathrm\; \{2f\}\}\; (t)\; =\; \{\backslash \; frac\; \{4V\; \_\; \{\backslash \; mathrm\; \{AC\_\; \{p\}\}\}\}\; \{3\; \backslash \; pi\}\}\; \backslash \; cos\; (2\; \backslash \; omega\; t)\}$

коэффициент пульсации определяется как:

$V rms = 1 T ∫ 0 T (4 В переменного тока p 3 π cos ⁡ (2 ω t)) 2 dt ⋅ ZRL, где ZRL - импеданс RL-фильтра, образованного дросселем и нагрузкой = 4 В переменного тока p 3 π 1 π [t 2 + sin ⁡ 2 ω t 4 ω] 0 π ⋅ RR 2 + XL 2 = 4 В переменного тока p 3 π 1 2 ⋅ RR 2 + XL 2 = 4 В переменного тока p 3 2 π ⋅ RXL. {\ displaystyle {\ begin {align} V _ {\ mathrm {rms}} = {} {\ sqrt {{\ frac {1} {T}} \ int _ {0} ^ {T} \ left ({\ frac {4V _ {\ mathrm {AC_ {p}}}} {3 \ pi}} \ cos (2 \ omega t) \ right) ^ {2} dt}} \ cdot Z _ {\ mathrm {RL}} \\ {\ text {where}} Z _ {\ mathrm {RL}} {\ text {- импеданс фильтра RL, образованного дросселем и нагрузкой}} \\ [8pt] = {} {\ frac {4V_ { \ mathrm {AC_ {p}}}} {3 \ pi}} {\ sqrt {{\ frac {1} {\ pi}} \ left [{\ frac {t} {2}} + {\ frac {\ sin 2 \ omega t} {4 \ omega}} \ right] _ {0} ^ {\ pi}}} \ cdot {\ frac {R} {\ sqrt {R ^ {2} + X _ {\ mathrm {L }} ^ {2}}}} = {\ frac {4V _ {\ mathrm {AC_ {p}}}} {3 \ pi}} {\ sqrt {\ frac {1} {2}}} \ cdot {\ frac {R} {\ sqrt {R ^ {2} + X _ {\ mathrm {L}} ^ {2}}}} = {\ frac {4V _ {\ mathrm {AC_ {p}}}} {3 {\ sqrt {2}} \ pi}} \ cdot {\ frac {R} {X _ {\ mathrm {L}}}}. \ end {align}}}$

Для $R\; \ll \; XL,\; R\; \backslash \; ll\; X\_\; \{L\},$

$VDC = (2 VAC p π) 2 - V rms 2 = 2 VAC p π, потому что V rms 2 = KR 2 XL 2 пренебрежимо мало для R ≪ XL. γ = V r m s V D C = 4 V A C p 3 2 π ⋅ R 2 ω L / 2 V A C p π = R 3 2 ω L. Подставив X L = 2 ω L, где L - индуктивность дросселя; в более привычной форме ≈ 0,471 R X L для R ≪ X L. {\ displaystyle {\ begin {align} V _ {\ mathrm {DC}} = {} {\ sqrt {\ left ({\ frac {2V _ {\ mathrm {AC_ {p}}}}} {\ pi}} \ справа) ^ {2} -V _ {\ mathrm {rms}} ^ {2}}} = {\ frac {2V _ {\ mathrm {AC_ {p}}}} {\ pi}} \ quad {\ text {потому что }} V _ {\ mathrm {rms}} ^ {2} = K {\ frac {R ^ {2}} {X _ {\ mathrm {L}} ^ {2}}} {\ text {несущественно для}} R \ ll X_ {L}. \\ [8pt] \ gamma = {} {\ frac {V _ {\ mathrm {rms}}} {V _ {\ mathrm {DC}}}} = \ left. {\ Frac {4V _ {\ mathrm {AC_ {p}}}} {3 {\ sqrt {2}} \ pi}} \ cdot {\ frac {R} {2 \ omega L}} \ right / {\ frac {2V_ { \ mathrm {AC_ {p}}}} {\ pi}} = {\ frac {R} {3 {\ sqrt {2}} \ omega L}}. \\ [8pt] {\ text {Substituting}} X _ {\ mathrm {L}} = 2 \ omega L, {\ text {где}} L {\ text {- индуктивность дросселя}}; {\ text {в более знакомой форме}} \\\ приблизительно {} 0,471 {\ frac {R} {X _ {\ mathrm {L}}}}, {\ text {for}} R \ ll X_ {L}. \ end {align}}}$

Это немного меньше 0,483, так как высшие гармоники не учитывались. (См. Индуктивность.)

Существует минимальная индуктивность (которая зависит от сопротивления нагрузки), необходимая для того, чтобы последовательный дроссель мог непрерывно проводить ток. Если индуктивность упадет ниже этого значения, ток будет прерывистым, а выходное постоянное напряжение повысится от среднего входного напряжения до пикового входного напряжения; по сути, индуктор будет вести себя как конденсатор. Эта минимальная индуктивность, называемая критической, равна $L\; =\; R\; 2\; \pi \; (3\; f)\; \{\backslash \; displaystyle\; L\; =\; \{\backslash \; frac\; \{R\}\; \{2\; \backslash \; pi\; (3f)\}\}\}$где R - сопротивление нагрузки, f - частота сети. Это дает значения L = R / 1131 (часто обозначаются как R / 1130) для выпрямления сети 60 Гц и L = R / 942 для выпрямления сети 50 Гц. Кроме того, прерывание тока в катушке индуктивности вызовет экспоненциальный коллапс ее магнитного потока; при падении тока возникает скачок напряжения, состоящий из очень высоких гармоник, которые могут повредить другие компоненты источника питания или цепи. Это явление называется.

Комплексный импеданс последовательного дросселя фактически является частью импеданса нагрузки, так что слабо нагруженные цепи имеют повышенную пульсацию (прямо противоположную входному фильтру конденсатора). По этой причине входной фильтр дросселя почти всегда является частью секции LC-фильтра, уменьшение пульсаций которого не зависит от тока нагрузки. Коэффициент пульсации:

$\gamma \; =\; V\; rms\; VDC\; =\; 2\; 3\; \cdot \; 1\; 4\; \omega \; 2\; CL\; \approx \; 0,471\; XCXL\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{rms\}\}\}\}\; \{V\; \_\; \{\backslash \; mathrm\; \{\; DC\}\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\}\}\; \{3\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{4\; \backslash \; omega\; ^\; \{2\}\; CL\}\}\; \backslash \; приблизительно\; 0,471\; \{\backslash \; frac\; \{X\; \_\; \{\backslash \; mathrm\; \{C\}\}\}\; \{X\; \_\; \{\backslash \; mathrm\; \{L\}\}\}\}\}$

где

• $\omega \; =\; 2\; \pi \; f\; \{\backslash \; displaystyle\; \backslash \; omega\; =\; 2\; \backslash \; pi\; f\}$

В цепях высокого напряжения / низкого тока, резистор может заменить последовательный дроссель в секции LC-фильтра (создавая секцию RC-фильтра). Это имеет эффект уменьшения выходного постоянного тока, а также пульсации. Коэффициент пульсации равен

$\gamma \; =\; V\; rms\; VDC\; =\; (1\; +\; RRL)\; 3\; 2\; \omega \; CR\; =\; 1\; 3\; 2\; \omega \; CR\; \approx \; 0,471\; XCR\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; \{\backslash \; frac\; \{V\; \_\; \{\backslash \; mathrm\; \{rms\}\}\}\; \{V\; \_\; \{\backslash \; mathrm\; \{DC\}\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; left\; (1\; +\; \{\backslash \; frac\; \{R\}\; \{R\; \_\; \{\backslash \; mathrm\; \{L\}\}\}\}\; \backslash \; right)\}\; \{3\; \{\backslash \; sqrt\; \{2\}\; \}\; \backslash \; omega\; CR\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{3\; \{\backslash \; sqrt\; \{2\}\}\; \backslash \; omega\; CR\}\}\; \backslash \; приблизительно\; 0,471\; \{\backslash \; frac\; \{X\; \_\; \{\backslash \; mathrm\; \{C\}\}\}\; \{R\}\}\}$если R L>>R, что делает секцию RC-фильтра практически независимой от нагрузки

, где

• $\omega \; =\; 2\; \pi \; f\; \{\backslash \; displaystyle\; \backslash \; omega\; =\; 2\; \backslash \; pi\; f\}$
• $R\; \{\backslash \; displaystyle\; R\}$- сопротивление резистора фильтра.

Аналогично, из-за независимости секций LC-фильтра от нагрузки, за резервуарным конденсатором также обычно следует конденсатор, что приводит к low-pass Π-фильтр. -Фильтр дает гораздо меньший коэффициент пульсаций, чем только конденсаторный или дроссельный входной фильтр. За ним могут следовать дополнительные секции LC- или RC-фильтра для дальнейшего снижения пульсаций до уровня, допустимого для нагрузки. Однако использование дросселей в современных конструкциях не рекомендуется по экономическим причинам.

Регулировка напряжения

Более распространенное решение, при котором требуется хорошее подавление пульсаций, - это использование накопительного конденсатора для уменьшения пульсаций до приемлемого уровня, а затем пропускание тока через схему регулятора напряжения. Схема регулятора не только обеспечивает стабильное выходное напряжение, но и отфильтровывает почти всю пульсацию, если минимальный уровень пульсации не опускается ниже регулируемого напряжения. Импульсные источники питания обычно включают в себя стабилизатор напряжения.

Регулирование напряжения основано на другом принципе, чем фильтрация: оно основывается на пиковом обратном напряжении диода или серии диодов для установки максимального выходного напряжения; он также может использовать одно или несколько устройств усиления напряжения, таких как транзисторы, для повышения напряжения во время провалов. Из-за нелинейных характеристик этих устройств выходной сигнал регулятора не имеет пульсаций. Простой регулятор напряжения может быть выполнен с последовательным резистором для падения напряжения, за которым следует шунтирующий стабилитрон, пиковое обратное напряжение которого (PIV) устанавливает максимальное выходное напряжение; при повышении напряжения диод отводит ток для поддержания стабилизации.

Влияние пульсаций

Пульсации нежелательны во многих электронных приложениях по ряду причин:

• пульсации представляют собой потерянную мощность, которая не может быть использована схемой, требующей постоянного тока
• пульсация вызовет нагрев компонентов цепи постоянного тока из-за того, что ток проходит через паразитные элементы, такие как ESR конденсаторов
• в источниках питания, пульсации напряжения требуют, чтобы пиковое напряжение компонентов было выше; ток пульсаций требует, чтобы паразитные элементы компонентов были ниже, а рассеиваемая способность была выше (компоненты будут больше, а качество должно быть выше)
• трансформаторы, которые подают ток пульсаций на емкостные входные цепи, должны иметь ВА номинальные значения, превышающие их номинальные значения нагрузки (ватт)
• Частота пульсаций и ее гармоники находятся в пределах звукового диапазона и поэтому будут слышны на таком оборудовании, как радиоприемники, оборудование для воспроизведения записей и профессиональное студийное оборудование.
• Частота пульсаций находится в пределах полосы пропускания телевизионного видео. Аналоговые телевизионные приемники будут демонстрировать узор движущихся волнистых линий, если присутствует слишком много пульсации.
• Наличие пульсаций может снизить разрешающую способность электронных испытательных и измерительных приборов. На осциллографе это проявляется в виде видимого рисунка на экране.
• В цифровых схемах он снижает порог, как и любая форма шума шины питания, при которой логические схемы выдают неправильные выходные данные и данные искажаются.

Пульсационный ток - это периодическая несинусоидальная форма волны, полученная от источника переменного тока, характеризующаяся импульсами с узкой полосой пропускания высокой амплитуды. Импульсы совпадают с пиковой или почти пиковой амплитудой сопутствующего синусоидального сигнала напряжения.

Пульсации тока приводят к увеличению рассеяния паразитных резистивных частей цепей, таких как ESR конденсаторов, DCR трансформаторов и катушек индуктивности, внутреннее сопротивление аккумуляторных батарей. Рассеивание пропорционально квадрату тока, умноженного на сопротивление (IR). Среднеквадратичное значение пульсирующего тока может во много раз превышать действующее значение тока нагрузки.

Пульсация на прототипе пятого порядка фильтр Чебышева

Пульсация в контексте частотной области относится к периодическому изменению вносимых потерь с частотой фильтра или другой двухпортовой сети. Не все фильтры демонстрируют пульсацию, некоторые имеют монотонно вносимые потери с частотой, такие как фильтр Баттерворта. Обычными классами фильтров, которые демонстрируют пульсации, являются фильтр Чебышева, обратный фильтр Чебышева и эллиптический фильтр. Пульсация обычно не является строго линейно-периодической, как видно из примера графика. Другими примерами сетей, демонстрирующих пульсации, являются сети согласования импеданса, которые были разработаны с использованием полиномов Чебышева. Пульсация этих сетей, в отличие от обычных фильтров, никогда не достигнет 0 дБ при минимальных потерях, если они предназначены для оптимальной передачи по всей полосе пропускания в целом.

За величину пульсации можно поторговаться. другие параметры в конструкции фильтра. Например, скорость спада от полосы пропускания до полосы задерживания может быть увеличена за счет увеличения пульсации без увеличения порядка фильтра. (то есть количество компонентов осталось прежним). С другой стороны, пульсацию можно уменьшить, увеличив порядок фильтра и в то же время поддерживая ту же скорость спада.

• Rectifier, не- линейное устройство, которое является основным источником пульсаций
• Dynamo, инструмент для выработки электроэнергии постоянного тока, на выходе которого присутствует большая составляющая пульсаций
• Звонок (сигнал), аналог частоты естественного отклика во временной области доменная рябь

• Райдер, Д.Д., Электронные основы и приложения, Pitman Publishing, 1970.
• Миллман-Халкиас, Integrated Electronics, McGraw-Hill Kogakusha, 1972.
• Маттей, Янг, Джонс, СВЧ-фильтры, сети согласования импеданса и структуры связи МакГроу-Хилл, 1964.