Координаты Риндлера

В релятивистской физике координаты гиперболически ускоренной системы отсчета важной и полезной координату диаграмма навигации, представляющая часть плоского пространства-времени Минковского. В специальной теории относительности равномернояющаяся части совершает гиперболическое движение, для которого равномерно ускоряющаяся система отсчета, в которой она покоится. может быть выбрана в правильного отсчета. Явления в этой системе с гиперболическим ускорением можно сравнить с эффектами, возникающими в однородном гравитационном поле. Для общего ускорения в плоском пространстве-времени см. Ускорение (специальная теория относительности) и Правильная система отсчета (плоское пространство-время).

В этой статье скорость света имеет значение как c = 1, инерциальные координаты - это (X, Y, Z, T), гиперболические координаты - (x, y, z, t). Эти гиперболические координаты можно разделить на два основных варианта в зависимости от положения ускоренного наблюдателя: если наблюдатель находится в момент времени T = 0 в позиции X = 1 / α (с α как константа собственное ускорение, измеренное с помощью сопутствующего акселерометр ), то гиперболические координаты часто называют координатами Риндлера с помощью метрикой Риндлера. Если наблюдатель находится в момент времени T = 0 в позиции X = 0, то иногда гиперболические координаты называют координатами Мёллера или координатами Коттлера-Мёллера с помощью метрикой Коттлера-Мёллера. Альтернативная карта, часто связанная с наблюдателями в гиперболическом движении, получается с использованием координат радара, которые иногда называют координатами Ласса. Как координаты Коттлера-Мёллера, так и координаты Ласса также обозначаются как координаты Риндлера.

Что касается истории, такие координаты введены вскоре после появления теории относительности, когда они были изучены частично с концепцией гиперболического движения: Относительно плоского пространства-времени Альберта Эйнштейна (1907, 1912), Макс Борн (1909), Арнольд Зоммерфельд (1910)), Макс фон Лауэ (1911), Хендрик Лоренц (1913), Фридрих Коттлер (1914), Вольфганг Паули (1921), (1922), Степан Мохорович (1922), Жорж Леметр (1924), Эйнштейн и Натан Розен (1935), Кристиан Мёллер (1943, 1952), Фриц Рорлих (1963), (1963), и в отношении как плоского, так и искривленного пространства-времени из общей теории относительности на Вольфганг Риндлер (1960, 1966). Подробности и источники см. В разделе по истории.

Содержание

• 1 Характеристики рамы Риндлера
• 2 Варианты формул преобразования
• 3 Наблюдатели Риндлера
• 4 «Парадоксальное» свойство
• 5 наблюдателей Минковского
• 6 Горизонт Риндлера
• 7 Геодезические
• 8 Метрика Ферма
• 9 Симметрии
• 10 Понятия расстояния
• 11 Обобщение на искривленное пространство-время
• 12 История
  • 12.1 Обзор
  • 12.2 Таблица с историческими формулами
• 13 См. Также
• 14 Ссылки
• 15 Исторические источники
• 16 Дополнительная литература

Характеристики рамы Риндлера

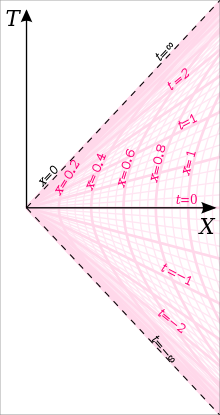
Диаграмма Риндлера, для $\alpha \; =\; 0,5\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 0,5\}$в уравнении (1a), нанесенном на диаграмму Минковского. Пункты тела в гиперболическом движении с постоянным собственным ускорением $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$в $по\; горизонтам\; Риндлера$

мировая линия X {\ displaystyle X}-направлении как функции собственного времени $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$и Скорость $\alpha \; \tau \; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; tau\}$может быть задана как

$T\; =\; x\; sinh\; \; (\alpha \; \tau ),\; X\; =\; x\; cosh\; \; (\alpha \; \tau )\; \{\backslash \; displaystyle\; T\; =\; x\; \backslash \; зп\; (\backslash \; альфа\; \backslash \; тау),\; \backslash \; квад\; Икс\; =\; х\; \backslash \; ш\; (\backslash \; альфа\; \backslash \; тау)\}$

где $х\; =\; 1\; /\; \alpha \; \{\backslash \; Displaystyle\; х\; =\; 1\; /\; \backslash \; альфа\}$- константа, а $\alpha \; \tau \; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; tau\}$- переменная, при этом мировая линия напоминает гиперболу $X\; 2\; -\; T\; 2\; =\; x\; 2\; \{\backslash \; Displaystyle\; X\; ^\; \{2\; \}\; -T\; ^\; \{2\}\; =\; x\; ^\; \{2\}\}$. Зоммерфельд показал, что уравнения можно интерпретировать заново, определив $x\; \{\backslash \; displaystyle\; x\}$как переменную и $\alpha \; \tau \; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; tau\}$как постоянную, так что он представляет собой одновременную "форму покоя" тела в гиперболическом движении, измеренную сопутствующим наблюдателем. Используя собственное время наблюдателя как время всего гиперболически ускоренного кадра, $\tau \; =\; t\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; t\}$, формулы преобразования между инерциальными координатами и гиперболическими координатами:

$T\; =\; Икс\; зп\; \; (\alpha \; т),\; Икс\; знак\; равно\; Икс\; сЬ\; \; (\alpha \; т),\; Y\; =\; Y,\; Z\; =\; Z\; \{\backslash \; Displaystyle\; Т\; =\; х\; \backslash \; зп\; (\backslash \; альфа\; т),\; \backslash \; четырехъядерный\; X\; =\; х\; \backslash \; сп\; (\backslash \; альфа\; т),\; \backslash \; quad\; Y\; =\; y,\; \backslash \; quad\; Z\; =\; z\}$

(1a)

с обратным

$t\; =\; 1\; \alpha \; arctanh\; \; (TX),\; x\; =\; Икс\; 2\; -\; Т\; 2,\; y\; =\; Y,\; z\; =\; Z\; \{\backslash \; displaystyle\; t\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; operatorname\; \{arctanh\}\; \backslash \; left\; (\{\backslash \; frac\; \{T\}\; \{X\}\}\; \backslash \; right),\; \backslash \; quad\; x\; =\; \{\backslash \; sqrt\; \{X\; ^\; \{2\}\; -T\; ^\; \{2\}\}\},\; \backslash \; quad\; y\; =\; Y,\; \backslash \; quad\; z\; =\; Z\}$

Дифференцированный и вставленный в метрику Минковского $ds\; 2\; =\; -\; d\; T\; 2\; +\; d\; X\; 2\; +\; d\; Y\; 2\; +\; d\; Z\; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; -\; dT\; ^\; \{2\}\; +\; dX\; ^\; \{2\}\; +\; dY\; ^\; \{2\}\; +\; dZ\; ^\; \{2\}\}$, метрика в кадре с гиперболическим ускорением следует за

$ds\; 2\; =\; -\; (\alpha \; x)\; 2\; dt\; 2\; +\; dx\; 2\; +\; dy\; 2\; +\; dz\; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; -\; (\backslash \; alpha\; x)\; ^\; \{2\}\; dt\; ^\; \{2\}\; +\; dx\; ^\; \{2\}\; +\; dy\; ^\; \{2\}\; +\; dz\; ^\; \{2\}\}$

(1b)

Эти преобразования определяют наблюдателя Риндлера как наблюдателя, который находится «в состоянии покоя» в координатах Риндлера, т. е. поддерживая постоянные x, y, z и изменяя только t с течением времени.. Координаты действительны в области , которую часто называют клином Риндлера, если $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$представляет правильное ускорение (вдоль гиперболы $x\; =\; 1\; \{\backslash \; displaystyle\; x\; =\; 1\}$) наблюдателя Риндлера, собственное время которого установлено равным координатному времени Риндлера. Чтобы поддерживать эту мировую линию, наблюдатель должен ускоряться с постоянным надлежащим ускорением, при этом наблюдатели Риндлера ближе к $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$(горизонт Риндлера ) с большим собственным ускорением. Все наблюдатели Риндлера мгновенно находятся в состоянии покоя в момент времени $T\; =\; 0\; \{\backslash \; displaystyle\; T\; =\; 0\}$в инерциальной системе отсчета, и в это время наблюдатель Риндлера с надлежащим ускорением $\alpha \; i\; \{\; \backslash \; displaystyle\; \backslash \; alpha\; \_\; \{i\}\}$будет в позиции $X\; =\; 1\; /\; \alpha \; i\; \{\backslash \; displaystyle\; X\; =\; 1\; /\; \backslash \; alpha\; \_\; \{i\}\}$(действительно $X\; =\; c\; 2\; /\; \alpha \; i\; \{\backslash \; displaystyle\; X\; =\; c\; ^\; \{2\}\; /\; \backslash \; alpha\; \_\; \{i\}\}$, но мы предполагаем единицу, где $c\; =\; 1\; \{\backslash \; displaystyle\; c\; =\; 1\}$), что также является постоянным расстоянием между наблюдателем от горизонта Риндлера в координатах Риндлера. Если все наблюдатели Риндлера устанавливают свои часы на ноль в $T\; =\; 0\; \{\backslash \; displaystyle\; T\; =\; 0\}$, то при определении системы координат Риндлера мы можем выбрать собственное время наблюдателя Риндлера. будет равно координатному времени $t\; \{\backslash \; displaystyle\; t\}$в координатах Риндлера, и собственное ускорение этого наблюдателя определяет значение $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$выше (для других наблюдателей Риндлера, находящихся на разных расстояниях от горизонта Риндлера, координатное время будет равноому постоянному кратному собственному времени). Обычно система координат Риндлера определяет так, чтобы наблюдатель Риндлера, это собственное время соответствует координатному времени, имел надлежащее ускорение $\alpha \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1\}$, так что $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$может быть исключен из соотношений.

Вышеупомянутое уравнение было упрощено для $c\; =\; 1\; \{\backslash \; displaystyle\; c\; =\; 1\}$. Непростое уравнение более удобно для определения расстояния Риндлера Горизонта с учетом ускорения $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$.

$t\; =\; c\; \alpha \; arctanh\; \; (c\; TX)\; \approx \; X\; \gg \; c\; T\; c\; 2\; T\; \alpha \; XX\; \approx \; c\; 2\; T\; \alpha \; t\; \approx \; T\; \approx \; tc\; 2\; \alpha \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; t\; =\; \{\backslash \; frac\; \{c\}\; \{\backslash \; alpha\}\}\; \backslash \; operatorname\; \{arctanh\}\; \backslash \; left\; (\{\backslash \; frac\; \{cT\}\; \{X\}\}\; \backslash \; right)\; \backslash ;\; \{\backslash \; overset\; \{X\; \backslash ,\; \backslash \; gg\; \backslash ,\; cT\}\; \{\backslash \; приблизительно\}\}\; \backslash ;\; \{\backslash \; frac\; \{c\; ^\; \{2\}\; T\}\; \{\backslash \; alpha\; X\}\}\; \backslash \backslash \; X\; \backslash \; приблизительно\; \{\backslash \; гидроразрыв\; \{c\; ^\; \{2\}\; T\}\; \{\backslash \; alpha\; t\}\}\; \backslash ;\; \{\backslash \; overset\; \{T\; \backslash ,\; \backslash \; приблизительно\; \backslash ,\; t\}\; \{\backslash \; приблизительно\}\}\; \backslash ;\; \{\backslash \; frac\; \{c\; ^\; \{2\}\}\; \{\backslash \; alpha\}\}\; \backslash \; end\; \{align\}\}\}$

Остальная часть статьи будет соответствовать соглашению по настройке, как $\alpha \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1\}$, так и $c\; =\; 1\; \{\backslash \; displaystyle\; c\; =\; 1\}$, поэтому единицы для $X\; \{\backslash \; displaystyle\; X\}$и $x\; \{\backslash \; displaystyle\; x\}$будут быть 1 единицей $=\; c\; 2\; /\; \alpha \; =\; 1\; \{\backslash \; displaystyle\; =\; c\; ^\; \{2\}\; /\; \backslash \; alpha\; =\; 1\}$. Помните, что настройка $\alpha \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1\}$световая секунда в секунду сильно отличается от настройки световых лет в год. Даже если мы выберем единицу, в которой $c\; =\; 1\; \{\backslash \; displaystyle\; c\; =\; 1\}$, качеего ускорения $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$будет зависеть по наш выбору единиц: например, если мы используем единицу световых лет для расстояния, ($X\; \{\backslash \; displaystyle\; X\}$или $x\; \{\backslash \; displaystyle\; x\}$) и годы для времени ($T\; \{\backslash \; displaystyle\; T\}$или $t\; \{\backslash \; displaystyle\; t\}$), это будет означать $\alpha \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1\}$световой год / год, равный примерно 9,5 метрам / секунду, тогда как мы используем единицу световых секунд для измерения расстояния, ($X\; \{\backslash \; displaystyle\; X\}$или $x\; \{\backslash \; displaystyle\; x\}$) и секунды для времени, ($T\; \{\backslash \; displaystyle\; T\}$или $t\; \{\backslash \; displaystyle\; t\}$), это будет означать $\alpha \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1\}$световая секунда в секунду, или 299 792 458 метров в секунду).

Варианты формул преобразования

Дается более общий вывод формул преобразования, когда формулируется соответствующая тетрада Ферми - Уокера, из которых координаты Ферми или Могут быть получены правильные координаты. В зависимости от выбора начала координат этих координат можно получить метрику, замедление времени между временем в начале координат $dt\; 0\; \{\backslash \; displaystyle\; dt\_\; \{0\}\}$и $dt\; \{\backslash \; displaystyle\; dt\}$в точке $x\; \{\backslash \; displaystyle\; x\}$, а координата световой скорости $|\; d\; x\; |\; /\; |\; д\; т\; |\; \{\backslash \; displaystyle\; |\; dx\; |\; /\; |\; dt\; |\}$(эта переменная скорость света не противоречит специальной теории относительности, потому что это всего артефакт ускоренных координат, в то время как в инерциальной координаты остаются постоянными). Вместо координат положения ФермиРеферентные координаты, получаемые путем определения расстояния с помощью световых сигналов (см. Разделение Понятия расстояния), по данному метрика, замедление времени и скорость света не зависит от больше координат - в, ориентирующая скорость света идентичной скорости света $(c\; =\; 1)\; \{\backslash \; displaystyle\; (c\; =\; 1)\}$в инерциальных кадрах:

$X\; \{\backslash \; displaystyle\; X\}$в $T\; =\; 0\; \{\backslash \; displaystyle\; T\; =\; 0\}$	Преобразование, метрика, замедление времени и координатная скорость света
$X\; =\; 0\; \{\backslash \; displaystyle\; X\; =\; 0\}$	Координаты Коттлера-Мёллера
	$T\; =\; (x\; +\; 1\; \alpha )\; sh\; \; (\alpha \; t)\; X\; =\; (x\; +\; 1\; \alpha )\; ch\; \; (\alpha \; t)\; -\; 1\; \alpha \; Y\; =\; y\; Z\; =\; zt\; =\; 1\; \alpha \; arctanh\; \; (TX\; +\; 1\; \alpha )\; x\; =\; (\; Икс\; +\; 1\; \alpha )\; 2\; -\; Т\; 2\; -\; 1\; \alpha \; Y\; знак\; равно\; Y\; Z\; =\; Z\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{array\}\; \{c\; |\; c\}\; \{\backslash \; begin\; \{выровнено\}\; T\; =\; \backslash \; left\; (x\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; right)\; \backslash \; sinh\; (\backslash \; alpha\; t)\; \backslash \backslash \; X\; =\; \backslash \; left\; (x\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; right)\; \backslash \; cosh\; (\backslash \; alpha\; t)\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \backslash \; Y\; =\; y\; \backslash \backslash \; Z\; =\; z\; \backslash \; end\; \{align\}\}\; \{\; \backslash \; begini\; n\; \{выровнено\}\; t\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; operatorname\; \{arctanh\}\; \backslash \; left\; (\{\backslash \; frac\; \{T\}\; \{X\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\}\}\}\; \backslash \; right)\; \backslash \; \backslash \; x\; =\; \{\backslash \; sqrt\; \{\backslash \; left\; (X\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; right)\; ^\; \{2\}\; -T\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; \backslash \; y\; =\; Y\; \backslash \backslash \; z\; =\; Z\; \backslash \; end\; \{align\}\}\; \backslash \; end\; \{array\}\}\}$ (2a) $ds\; 2\; =\; -\; (1\; +\; \alpha \; x)\; 2\; dt\; 2\; +\; dx\; 2\; +\; dy\; 2\; +\; dz\; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; -\; (1+\; \backslash \; alpha\; x)\; \{\}\; ^\; \{2\}\; dt\; ^\; \{2\}\; +\; dx\; ^\; \{2\}\; +\; dy\; ^\; \{2\; \}\; +\; dz\; ^\; \{2\}\}$ (2b) $dt\; =\; (1\; +\; \alpha \; x)\; dt\; 0,\; |\; d\; x\; |\; |\; д\; т\; |\; Знак\; равно\; 1\; +\; \alpha \; Икс\; \{\backslash \; Displaystyle\; dt\; =\; (1+\; \backslash \; alpha\; x)\; dt\_\; \{0\},\; \backslash \; qquad\; \{\backslash \; frac\; \{|\; dx\; |\}\; \{|\; dt\; |\}\}\; =\; 1+\; \backslash \; alpha\; x\}$ (2c)
	Координаты Риндлера
$X\; =\; 1\; \alpha \; \{\backslash \; displaystyle\; X\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\}$	$T\; знак\; равно\; Икс\; sinh\; \; (\alpha \; T)\; Икс\; =\; Икс\; cosh\; \; (\alpha \; T)\; Y\; =\; YZ\; =\; zt\; =\; 1\; \alpha \; arctanh\; \; TX\; x\; =\; X\; 2\; -\; T\; 2\; Y\; =\; Y\; Z\; =\; Z\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{c\; |\; c\}\; \{\backslash \; begin\; \{align\}\; T\; =\; x\; \backslash \; sinh\; (\backslash \; alpha\; t)\; \backslash \backslash \; X\; =\; x\; \backslash \; cosh\; (\backslash \; alpha\; t)\; \backslash \backslash \; Y\; =\; y\; \backslash \backslash \; Z\; =\; z\; \backslash \; end\; \{align\}\}\; \{\backslash \; begin\; \{align\}\; t\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; operatorname\; \{arctanh\}\; \{\backslash \; frac\; \{T\}\; \{X\}\}\; \backslash \backslash \; x\; =\; \{\backslash \; sqrt\; \{X\; ^\; \{2\}\; -T\; ^\; \{2\}\}\}\; \backslash \backslash \; y\; =\; Y\; \backslash \backslash \; z\; =\; Z\; \backslash \; конец\; \{выровненный\}\}\; \backslash \; конец\; \{массив\}\}\}$ (2d) $ds\; 2\; =\; -\; (\alpha \; x)\; 2\; dt\; 2\; +\; dx\; 2\; +\; dy\; 2\; +\; dz\; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; -\; (\backslash \; alpha\; x)\; ^\; \{2\}\; dt\; ^\; \{2\}\; +\; dx\; ^\; \{2\}\; +\; dy\; ^\; \{2\}\; +\; dz\; ^\; \{2\}\}$ (2e) $dt\; =\; \alpha \; xdt\; 0,\; |\; d\; x\; |\; |\; д\; т\; |\; =\; \alpha \; Икс\; \{\backslash \; Displaystyle\; dt\; =\; \backslash \; alpha\; x\; \backslash \; dt\_\; \{0\},\; \backslash \; qquad\; \{\backslash \; frac\; \{|\; dx\; |\}\; \{|\; dt\; |\}\}\; =\; \backslash \; alpha\; x\}$ (2f)
	Координаты радара (Координаты Ласса)
$X\; =\; 1\; \alpha \; \{\backslash \; displaystyle\; X\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\}$	$T\; =\; 1\; \alpha \; e\; \alpha \; x\; sinh\; \; (\alpha \; t)\; X\; =\; 1\; \alpha \; e\; \alpha \; x\; соз\; \; (\alpha \; T)\; Y\; знак\; равно\; YZ\; =\; zt\; =\; 1\; \alpha \; arctanh\; \; TX\; x\; =\; 1\; 2\; \alpha \; ln\; \; [\alpha \; 2\; (\; Икс\; 2\; -\; Т\; 2)]\; Y\; =\; Y\; Z\; =\; Z\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{c\; |\; c\}\; \{\backslash \; begin\; \{align\}\; T\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; e\; ^\; \{\backslash \; alpha\; x\}\; \backslash \; sinh\; (\backslash \; alpha\; t)\; \backslash \backslash \; X\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\; \}\}\; e\; ^\; \{\backslash \; alpha\; x\}\; \backslash \; cosh\; (\backslash \; alpha\; t)\; \backslash \backslash \; Y\; =\; y\; \backslash \backslash \; Z\; =\; z\; \backslash \; end\; \{align\}\}\; \{\backslash \; begin\; \{align\}\; t\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\; \backslash \; operatorname\; \{arctanh\}\; \{\backslash \; frac\; \{T\}\; \{X\}\}\; \backslash \backslash \; x\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; alpha\}\}\; \backslash \; ln\; \backslash \; left\; [\backslash \; alpha\; \{\}\; ^\; \{2\}\; \backslash \; left\; (X\; ^\; \{2\}\; -T\; ^\; \{2\}\; \backslash \; right)\; \backslash \; right]\; \backslash \backslash \; y\; =\; Y\; \backslash \backslash \; z\; =\; Z\; \backslash \; end\; \{align\}\}\; \backslash \; end\; \{array\}\}\}$ (2g)
	$ds\; 2\; знак\; равно\; е\; 2\; \alpha \; Икс\; (-\; dt\; 2\; +\; dx\; 2)\; +\; dy\; 2\; +\; dz\; 2\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; e\; ^\; \{2\; \backslash \; alpha\; x\}\; \backslash \; left\; (-dt\; ^\; \{\; 2\}\; +\; dx\; ^\; \{2\}\; \backslash \; right)\; +\; dy\; ^\; \{2\}\; +\; dz\; ^\; \{2\}\}$ (2h) $dt\; =\; e\; \alpha \; xdt\; 0,\; |\; d\; x\; |\; |\; д\; т\; |\; Знак\; равно\; 1\; \{\backslash \; displaystyle\; dt\; =\; e\; ^\; \{\backslash \; alpha\; x\}\; dt\_\; \{0\},\; \backslash \; qquad\; \{\backslash \; frac\; \{|\; dx\; |\}\; \{|\; dt\; |\}\}\; =\; 1\}$ (2i)

Наблюдатели Риндлера

В новой диаграмме (1a) с $c\; =\; 1\; \{\backslash \; displaystyle\; c\; =\; 1\}$и $\alpha \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1\}$, естественно взять поле coframe

$d\; \sigma \; 0\; =\; xdt,\; d\; \sigma \; 1\; =\; dx,\; d\; \sigma \; 2\; =\; dy,\; d\; \sigma \; 3\; знак\; равно\; dz\; \{\backslash \; displaystyle\; d\; \backslash \; sigma\; ^\; \{0\}\; =\; x\; \backslash ,\; dt,\; \backslash ;\; \backslash ;\; d\; \backslash \; sigma\; ^\; \{1\}\; =\; dx,\; \backslash ;\; \backslash ;\; d\; \backslash \; sigma\; ^\; \{2\}\; =\; dy,\; \backslash ;\backslash ;\; d\; \backslash \; sigma\; ^\; \{3\}\; =\; dz\}$

с двойным фреймовым полем

$e\; \to \; 0\; =\; 1\; x\; \partial \; t,\; e\; \to \; 1\; =\; \partial \; x,\; e\; \to \; 2\; =\; \partial \; y,\; e\; \to \; 3\; =\; \partial \; Z\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{e\}\}\; \_\; \{0\}\; =\; \{\backslash \; frac\; \{1\}\; \{x\}\}\; \backslash \; partial\; \_\; \{t\},\; \backslash ;\; \backslash ;\; \{\backslash \; vec\; \{e\}\}\; \_\; \{1\}\; =\; \backslash \; partial\; \_\; \{x\},\; \backslash ;\; \backslash ;\; \{\backslash \; vec\; \{e\}\}\; \_\; \{2\}\; =\; \backslash \; partial\; \_\; \{y\},\; \backslash ;\; \backslash ;\; \{\backslash \; vec\; \{e\}\}\; \_\; \{3\}\; =\; \backslash \; partial\; \_\; \{z\}\}$

Это определяет локальный фрейм Лоренца в касательном пространстве в каждом событии (в области, охватываемой нашей диаграммой Риндлера, а именно в области клина Риндлера). интегральные кривые timelike единичного использования поля $e\; \to \; 0\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; vec\; \{e\}\}\; \_\; \{0\}\}$дают времяподобное сравнение, состоящее из ряда линий семейства наблюдателей, называемых наблюдателями Риндлера. На диаграмме Риндлера эти мировые линии представлены как вертикальные координатные линии $x\; =\; x\; 0,\; y\; =\; y\; 0,\; z\; =\; z\; 0\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; x\; \backslash ;\; знак\; равно\; x\_\; \{0\},\; \backslash ;\; у\; \backslash ;\; знак\; равно\; y\_\; \{0\},\; \backslash ;\; z\; \backslash ;\; знак\; равно\; z\_\; \{0\}\}$. Используя преобразование координат выше, мы обнаруживаем, что они соответствуют гиперболическим дугам в исходной декартовой карте.

Некоторые типичные наблюдатели Риндлера (темно-синие гиперболические дуги) изображены с помощью декартовой карты. Красные линии под углом 45 градусов от вертикали представить горизонт Риндлера; система координат Риндлера определена только справа от этой границы.

Как и любое времяподобное сравнение в любом лоренцевом множестве, это сравнение имеет кинематическое разложение (см. уравнение Райчаудхури ). В этом случае расширение и завихренность конгруэнтности наблюдателей Риндлера исчезают. Исчезновение тензора расширения означает, что каждый из наших наблюдателей передает постоянное расстояние до своих соседей. Исчезновение тензора завихренности означает, что мировые линии наших наблюдателей не скручиваются друг относительно друга; это своего рода локальное отсутствие «закрутки».

вектор ускорения каждого наблюдателя задается ковариантной производной

$\nabla \; e\; \to \; 0\; e\; \to \; 0\; =\; 1\; xe\; \to \; 1\; \{\backslash \; displaystyle\; \backslash \; nabla\; \_\; \{\{\backslash \; vec\; \{e\}\; \}\; \_\; \{0\}\}\; \{\backslash \; vec\; \{e\}\}\; \_\; \{0\}\; =\; \{\backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; vec\; \{e\}\}\; \_\; \{1\}\}$

То есть, каждый наблюдатель Риндлера ускоряется в направлении $\partial \; x\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; partial\; \_\; \{x\}\}$. По отдельной, каждый наблюдатель фактически ускоряется с постоянной величиной в этом направлении, поэтому их мировые линии являются локальными аналогами окружения, которые являются кривыми постоянной кривизны траектории в евклидовой геометрии.

Наблюдатели Риндлера не имеют завихренности, они также ортогональны гиперповерхности. Ортогональные пространственные гиперсрезы: $t\; =\; t\; 0\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; t\; \backslash ;\; знак\; равно\; t\_\; \{0\}\}$; они представлены как горизонтальные полуплоскости на диаграмме Риндлера и как полуплоскости через $T\; =\; X\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; T\; \backslash ;\; знак\; равно\; ИКС\; \backslash ;\; знак\; равно\; 0\}$в декартовой карте (см. Рисунок выше). Установив $dt\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; dt\; \backslash ;\; знак\; равно\; 0\}$в линейном элементе, мы увидим, что они имеют обычную евклидову геометрию, $d\; \sigma \; 2\; =\; dx\; 2\; +\; dy\; 2\; +\; dz\; 2,\; \forall \; Икс>0,\; \forall \; Y,\; Z\; \{\backslash \; Displaystyle\; \backslash \; scriptstyle\; d\; \backslash \; sigma\; ^\; \{2\}\; \backslash ;\; знак\; равно\; dx\; ^\; \{2\}\; \backslash ,\; +\; \backslash ,\; dy\; ^\; \{2\}\; \backslash ,\; +\; \backslash ,\; dz\; ^\; \{2\},\; \backslash ;\; \backslash \; forall\; x\; \backslash ,>\backslash ,\; 0,\; \backslash ;\; \backslash \; forall\; y,\; \backslash ,\; z\}$.

A «парадоксальное» свойство

пространственные координаты на диаграмме Риндлера очень простую интерпретацию.>Обратите внимание, что наблюдатели Риндлера с меньшими координатами ускоряются с трудом x ускоряются с трудом. стержня, который ускоряется некоторой внешней внешней (параллельной его оси симметрии), должен ускоряться немного сильнее, чем ведущий конец, иначе он должен в конечном итоге сломаться. 620>Лоренцево сокращение. стержень ускоряется, его скорость увеличивается, а длина уменьшается. Он становится короче, задняя часть должна ускоряться сильнее, чем передняя. Другой способ взглянуть на это: серверная часть должна достичь такого же изменения скорости за более короткий период времени. Это приводит к диаграмме уравнения, показывающему, что на некотором расстоянии ускорение заднего конца расходится, что приводит к горизонту Риндлера.

. Это явление лежит в основе хорошо известного «парадокса», космического корабля Белла. парадокс. Однако это простое следствие релятивистской кинематики. Один из способов увидеть это - заметить, что момент времени ускорения - это просто кривизна траектории настоящей мировой линии. Мировые линии наших наблюдателей Риндлера являются аналогами семейства концентрических кругов на евклидовой плоскости, поэтому мы просто имеем дело с лоренцевым аналогом факта, знакомого конькобежцам: в семье концентрических кругов{\displaystyle \alpha \tau }<7><8>\alpha _{{i}}<8><9>\scriptstyle t \;=\; 0<9><10>{\displaystyle T<11>{\displaystyle T=x\sinh(\alpha t),\quad X=x\cosh(\alpha t),\quad Y=y,\quad Z=z}<11><12>c=1<12><13>\scriptstyle 0 \,<\, x \,<\, \frac{E}{\sqrt{P^2 \,+\, Q^2}}<13><14>\begin{align} \exp(\pm t) \, \left( \frac{y}{x} \, \partial_t \pm \left[ y \, \partial_x - x \, \partial_y \right] \right)\\ \exp(\pm t) \, \left( \frac{z}{x} \, \partial_t \pm \left[ z \, \partial_x - x \, \partial_z \right] \right)\\ \exp(\pm t) \, \left( \frac{1}{x} \, \partial_t \pm \partial_x \right) \end{align}<14><15>\begin{align} \vec{f}_0 = \frac{1}{x}\cosh(t) \, \partial_t - \sinh(t) \, \partial_x\\ \vec{f}_1 = -\frac{1}{x}\sinh(t) \, \partial_t + \cosh(t) \, \partial_x\\ \vec{f}_2 = \partial_y, \; \vec{f}_3 = \partial_z \end{align}<15><16> \dot{t} = \frac{E}{x^2}, \; \; \dot{y} = P, \; \; \dot{z} = Q <16><17> x_0 \, \log \left(1 + \frac{h}{x_0} \right) = h - \frac{h^2}{2 \, x_0} + O \left( h^3 \right) <17><18>{\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}\xi _{1}=x_{1}\cosh \alpha x_{4}\\\xi _{2}=x_{2}\\\xi _{3}=x_{3}\\\xi _{4}=x_{1}\sinh \alpha x_{4}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx_{1}^{2}-dx_{2}^{2}-dx_{3}^{2}+\alpha {}^{2}x_{1}^{2}dx_{4}^{2}\end{matrix}}}<18><19>\scriptstyle\vec{e}_0<19><20>{\displaystyle X=c^{2}/\alpha _{i}}<20><21>{\displaystyle c^{2}/\alpha +x}<21><22>\scriptstyle dt \;=\; 0<22><23>\scriptstyle t \;=\; t_0,\; x \;=\; x_0,\; y \;=\; y_0,\; z \;=\; z_0<23><24>\begin{align} t - t_0 = \operatorname{arctanh} \left( \frac{1}{E}\left[s \left(P^2 + Q^2\right) - \sqrt{E^2 - \left(P^2 + Q^2\right) x_0^2}\right] \right) +\\ \quad\quad \operatorname{arctanh} \left( \frac{1}{E}\sqrt{E^2 - (P^2+Q^2) x_0^2} \right)\\ x = \sqrt{ x_0^2 + 2s \sqrt{E^2 - (P^2+Q^2) x_0^2} - s^2 (P^2 + Q^2) }\\ y - y_0 = Ps;\;\; z - z_0 = Qs \end{align}<24><25>{\displaystyle ds^{2}=e^{2\alpha x}\left(-dt^{2}+dx^{2}\right)+dy^{2}+dz^{2}}<25><26>t<26><27>\vec{f}_0 = \partial_T, \; \vec{f}_1 = \partial_X, \; \vec{f}_2 = \partial_Y, \; \vec{f}_3 = \partial_Z <27><28>{\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}x=x<28><29>X<29><30>\scriptstyle x \;=\; x_0, \; y \;=\; 0,\; z \;=\; 0<30><31> ds^2 = g_{00} \, dt^2 + g_{jk} \, dx^j \, dx^k,\;\; j,\; k \in \{1, 2, 3\} <31><32>\scriptstyle x_0 \;=\; 1<32><33>{\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}x=x<33><34>{\displaystyle {\scriptstyle {\begin{matrix}dc={\frac {g}{c}}dz\\\hline {\begin{aligned}z=a\left(z<34><35>\scriptstyle dy \;=\; dz \;=\; 0<35><36>{\displaystyle ds^{2}=-(1+\alpha x){}^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}<36><37>\scriptstyle T \;=\; X \;=\; 0<37><38>\scriptstyle E<38><39>{\displaystyle {\scriptstyle {\begin{matrix}\sigma =\tau \left(1+{\frac {\gamma \xi }{c^{2}}}\right)\\\sigma =\tau e^{\gamma \xi /c^{2}}\\c\left(1+{\frac {\gamma \xi }{c^{2}}}\right)\end{matrix}}}}<39><40>{\displaystyle t={\frac {1}{\alpha }}\operatorname {arctanh} \left({\frac {T}{X}}\right),\quad x={\sqrt {X^{2}-T^{2}}},\quad y=Y,\quad z=Z}<40><41>x=0<41><42>\scriptstyle\partial_x<42><43>\scriptstyle \partial_t<43><44>{\displaystyle {\scriptstyle {\begin{matrix}ds^{2}=c^{2}\left(1+{\frac {\gamma _{0}x}{c^{2}}}\right)d\tau ^{2}-dx^{2}-dy^{2}-dz^{2}\\\hline ds^{2}=g_{44}dx_{4}^{2}+g_{11}dx_{1}^{2}+g_{22}\left(dx_{2}^{2}+dx_{3}^{2}\right)\\{\boldsymbol {\downarrow }}\\V<44><45>{\displaystyle {\scriptstyle {\begin{matrix}{\text{Mohorovičić (1922):}}\\g_{11}=g_{44}=V^{2},\ VV<45><46>{\displaystyle X^{2}-T^{2}=x^{2}}<46><47> \dot{x}^2 = \left(\epsilon + \frac{E^2}{x^2} \right) - P^2 - Q^2<47><48>{\displaystyle \scriptstyle {\begin{matrix}{\begin{matrix}c_{1}^{(1)}=0,c_{1}^{(2)}=0,c_{1}^{(3)}={\frac {1}{i}}\sinh u,c_{1}^{(4)}=\cosh u,\\c_{2}^{(1)}=0,c_{2}^{(2)}=0,c_{2}^{(3)}={\frac {1}{i}}\cosh u,c_{2}^{(4)}=-\sinh u,\\c_{3}^{(1)}=1,c_{3}^{(2)}=0,c_{3}^{(3)}=0,c_{3}^{(4)}=0,\\c_{4}^{(1)}=0,c_{4}^{(2)}=1,c_{4}^{(3)}=0,c_{4}^{(4)}=0,\end{matrix}}\\{\boldsymbol {\downarrow }}\\X=x+\Delta ^{(2)}c_{2}+\Delta ^{(3)}c_{3}+\Delta ^{(4)}c_{4}\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X=x_{0}+{\mathfrak {X}}<48><49>\scriptstyle x \;=\; x_0 \,+\, h, \; y \;=\; 0,\; \; z \;=\; 0<49><50>{\displaystyle \scriptstyle {\begin{aligned}X=R\cos \varphi \\L=R\sin \varphi \\R^{2}=X^{2}+L^{2}\\\tan \varphi ={\frac {L}{X}}\end{aligned}}}<50><51>\scriptstyle x \;=\; 0<51><52>\nabla_{\vec{e}_0} \vec{e}_0 = \frac{1}{x}\vec{e}_1<52><53>{\displaystyle ds^{2}=-dT^{2}+dX^{2}+dY^{2}+dZ^{2}}<53><54>\scriptstyle \epsilon \;=\; -x^2 \, \dot{t}^2 \,+\, \dot{x}^2 \,+\, \dot{y}^2 \,+\, \dot{z}^2<54><55>\scriptstyle s \,\in\, \left\{-\frac{1}{2},\; 0,\; \frac{1}{2}\right\}<55><56>{\displaystyle X/\left(X^{2}-T^{2}\right)>0}<56><57> \ddot{t} + \frac{2}{x} \, \dot{x} \, \dot{t} = 0, \; \ddot{x} + x \, \dot{t}^2 = 0, \; \ddot{y} = 0, \; \ddot{z} = 0<57><58>{\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}1+g\xi =(1+gx)\cosh gt\\g\tau =(1+gx)\sinh gt\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-dx^{2}-dy^{2}-dz^{2}+(1+gx)^{2}dt^{2}\end{matrix}}}}<58><59>{\displaystyle d\sigma ^{0}=x\,dt,\;\;d\sigma ^{1}=dx,\;\;d\sigma ^{2}=dy,\;\;d\sigma ^{3}=dz}<59><60>{\displaystyle {\scriptstyle {\begin{matrix}{\begin{aligned}x^{(1)}=x_{0}^{(1)}\\x^{(2)}=x_{0}^{(2)}\\x^{(3)}=b\cos iu\\x^{(4)}=b\sin iu\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=-c^{2}d\tau ^{2}=b^{2}(du)^{2}\\{\boldsymbol {\downarrow }}\\{\begin{matrix}c_{1}^{(1)}=0,c_{1}^{(2)}=0,c_{1}^{(3)}=-\sin iu,c_{1}^{(4)}=\cos iu,\\c_{2}^{(1)}=0,c_{2}^{(2)}=0,c_{2}^{(3)}=-\cos iu,c_{2}^{(4)}=-\sin iu,\end{matrix}}\\{\boldsymbol {\downarrow }}\\dS^{2}=(dX<60><61>x<61><62> d\rho^2 = \frac{1}{x^2}\left(dx^2 + dy^2 + dz^2\right),\;\; \forall x>0,\;\; \forall y, z<62><63>x=1<63><64>\scriptstyle d\sigma^2 \;=\; dx^2 \,+\, dy^2 \,+\, dz^2,\; \forall x\,>\,0,\; \forall y,\, z<64><65>{\displaystyle X^{2}-T^{2}>0}<65><66>\scriptstyle x \;=\; x_0,\; y \;=\; y_0,\; z \;=\; z_0<66><67>{\displaystyle \scriptstyle {\begin{matrix}{\begin{aligned}x^{1}=\varrho \cos \varphi \\x^{4}=\varrho \sin \varphi \end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=\left(d\xi ^{1}\right)^{2}+\left(d\xi ^{2}\right)^{2}+\left(d\xi ^{3}\right)^{2}+\left(\xi ^{1}\right)^{2}\left(d\xi ^{4}\right)^{2}\\\left(\xi ^{(1)}=\varrho,\ \xi ^{(2)}=x^{(2)},\ \xi ^{(3)}=x^{(3)},\ \xi ^{(4)}=\varphi \right)\end{matrix}}}<67><68>\scriptstyle s<68><69>{\displaystyle =c^{2}/\alpha =1}<69><70>{\displaystyle T=x\sinh(\alpha \tau),\quad X=x\cosh(\alpha \tau)}<70><71>\scriptstyle\vec{f}_0<71><72>{\displaystyle t-t_{0}=\log \left({\frac {x}{x_{0}}}\right)}<72><73>\alpha <73><74>{\displaystyle X=0}<74><75>\scriptstyle t \;=\; t_0<75><76>{\displaystyle \scriptstyle {\begin{aligned}x=r\cos \varphi \\y=y<76><77> \vec{e}_0 = \frac{1}{x}\partial_t,\;\; \vec{e}_1 = \partial_x,\;\; \vec{e}_2 = \partial_y,\;\; \vec{e}_3 = \partial_z<77><78>T=0<78><79>T<79><80>\begin{align} t = \operatorname{arctanh}\left(\frac{s}{x_0}\right),\; -x_0 <81>\scriptstyle\frac{E^2}{x^2} \,-\, P^2 \,-\, Q^2<81><82>{\displaystyle ds^{2}=-(\alpha x)^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}<82><83>{\displaystyle dt_{0}}<83><84>\tau=t<84><85> \partial_t, \; \; \partial_y, \; \; \partial_z, \; \; -z \, \partial_y + y \, \partial_z <85><86>{\displaystyle {\begin{array}{c|c}{\begin{aligned}T=x\sinh(\alpha t)\\X=x\cosh(\alpha t)\\Y=y\\Z=z\end{aligned}}{\begin{aligned}t={\frac {1}{\alpha }}\operatorname {arctanh} {\frac {T}{X}}\\x={\sqrt {X^{2}-T^{2}}}\\y=Y\\z=Z\end{aligned}}\end{array}}}<86><87>\scriptstyle h \,+\, \frac{1}{x_0} \,+\, O \left( h^3 \right) <87><88>{\displaystyle (c=1)}<88><89>\alpha =1<89><90>{\displaystyle {\scriptstyle {\begin{matrix}x=-q\xi,\ y=\eta,\ z=\zeta,\ t={\frac {p}{c^{2}}}\xi \\\left(p=x_{\tau },\ q=-t_{\tau }={\sqrt {1+p^{2}/c^{2}}}\right)\\{\boldsymbol {\downarrow }}\\x^{2}-c^{2}t^{2}=\xi ^{2}\end{matrix}}}}<90><91>\tau <91><92>\scriptstyle \partial_T<92><93>{\displaystyle {\begin{array}{c|c}{\begin{aligned}T={\frac {1}{\alpha }}e^{\alpha x}\sinh(\alpha t)\\X={\frac {1}{\alpha }}e^{\alpha x}\cosh(\alpha t)\\Y=y\\Z=z\end{aligned}}{\begin{aligned}t={\frac {1}{\alpha }}\operatorname {arctanh} {\frac {T}{X}}\\x={\frac {1}{2\alpha }}\ln \left[\alpha {}^{2}\left(X^{2}-T^{2}\right)\right]\\y=Y\\z=Z\end{aligned}}\end{array}}}<93><94>\scriptstyle t \,=\, 0<94><95>{\displaystyle {\scriptstyle {\begin{matrix}d\xi ^{2}-d\tau ^{2}=dx^{2}-c^{2}dt^{2}\\{\boldsymbol {\downarrow }}\\c=c_{0}+ax\\{\boldsymbol {\downarrow }}\\{\begin{aligned}\xi =x+{\frac {ac}{2}}t^{2}\\\eta =y\\\zeta =z\\\tau =ct\end{aligned}}\end{matrix}}}}<95><96>x_{1}<96><97>{\displaystyle X=1/\alpha _{i}}<97><98>{\displaystyle \scriptstyle {\begin{matrix}\alpha _{ik}=\left({\begin{matrix}U_{4}/ic00iU_{1}/c\\0100\\0010\\U_{1}/ic00U_{4}/ic\end{matrix}}\right)\\U_{i}=\left(c\sinh {\frac {g\tau }{c}},\ 0,0,\ ig\cosh {\frac {g\tau }{c}}\right)\\{\boldsymbol {\downarrow }}\\X_{i}=\mathbf {f} _{i}(t)+x^{\prime \kappa }\alpha _{\kappa i}(\tau)\\{\boldsymbol {\downarrow }}\\{\begin{aligned}X={\frac {c^{2}}{g}}\left(\cosh {\frac {gt}{c}}-1\right)+x\cosh {\frac {gt}{c}}\\Y=y\\Z=z\\T={\frac {c}{g}}\sinh {\frac {gt}{c}}+x{\frac {\sinh {\frac {gt}{c}}}{c}}\end{aligned}}\\{\boldsymbol {\downarrow }}\\ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}\left(1+gx/c^{2}\right)^{2}\\\\\end{matrix}}}<98><99>{\displaystyle X={\frac {1}{\alpha }}}<99><100>{\displaystyle {\scriptstyle {\begin{aligned}x^{(1)}=x_{0}^{(1)}\\x^{(2)}=x_{0}^{(2)}\\x^{(3)}=b\cos i\varphi \\x^{(4)}=b\sin i\varphi \end{aligned}}}}<100><101>{\displaystyle dt=(1+\alpha x)dt_{0},\qquad {\frac {|dx|}{|dt|}}=1+\alpha x}<101><102>\scriptstyle h \,>\, 0<102><103>dt<103><104>{\displaystyle |dx|/|dt|}<104><105>\scriptstyle\epsilon \;\in\; \left\{-1,\, 0,\, 1\right\}<105><106>{\displaystyle dt=e^{\alpha x}dt_{0},\qquad {\frac{|dx|}{|dt|}}=1}<106><107>{\displaystyle {\scriptstyle 0\,<\,X\,<\,\infty,\;-X\,<\,T\,<\,X}}<107><108>{\displaystyle dt=\alpha x\ dt_{0},\qquad {\frac {|dx|}{|dt|}}=\alpha x}<108><109> d\rho^2 = \frac{1}{-g_{00}}\left(g_{jk} \, dx^j \, dx^k\right)<109>html